2. 中国地质调查局广州海洋地质调查局,广州市海滨路1133号,511458
GRACE/GRACE-FO(GFO)任务可为观测大气层、水圈、海洋等地球圈层的大尺度质量变化提供全新视角。GRACE/GFO球谐系数模型主要由得克萨斯大学空间研究中心(CSR)、德国波茨坦地学研究中心(GFZ)、喷气推进实验室(JPL)3个机构提供。不同机构对原始重力观测数据的处理策略存在差异[1],但反演结果均存在明显的南北条带噪声。
滤波器的应用对于减少GRACE/GFO球谐系数模型中的噪声至关重要,最常用的滤波算法为高斯滤波[2]。Swenson等[3]基于南北条带噪声特性提出一种滑动窗口去相关滤波。在该方法基础上,部分学者通过调整拟合范围、窗口长度和多项式拟合次数,提出多种方法,如PnMl(P4M6)方法[4]等。然而,仅应用PnMl(P4M6)方法的反演结果在低纬度区域(30°S~30°N)仍存在明显的南北条带噪声。
为进一步提升PnMl方法在低纬度区域的去条带效果,本文提出一种改进的PnMl方法。首先在GRACE/GFO球谐系数模型上应用改进方法,讨论其在时域、空域和频域的性能;然后采用信噪比(signal-to-noise ratio,SNR)指标和广义三角帽方法(three-cornered hat,TCH)对改进方法进行量化评估。
1 数据和处理方法 1.1 数据本研究采用3大机构(CSR、JPL、GFZ)2002-04~2019-09的GRACE/GFO月时变重力场模型(即球谐系数模型)估计全球质量场变化。将模型截断至60阶次并移除背景重力场(平均重力场),获得月重力场变化量。球谐系数模型的一阶项由GRACE/GFO数据结合海洋数值模型确定[5],C20和C30项由相应的高精度卫星激光测距结果替代[6-7],冰川均衡改正则采用ICE-6G_D模型[8]。此外,采用CSR发布的RL06版本GRACE/GFO 0.25°×0.25° Mascon产品(CSR-RL06M v02),记为CSR-M[9]。除椭球效应外,CSR-M采用与球谐系数模型解相同的改正和替换。
1.2 利用球谐系数产品反演全球质量场变化以等效水柱高(EWH)表示的全球质量场变化Δh可由GRACE/GFO球谐系数模型计算[2]:
| $ \begin{gathered} \Delta h(\theta, \lambda)=\frac{R \rho_e}{3 \rho_w} \sum\limits_{n=0}^{n_{\max }} \sum\limits_{m=0}^n P_{n m}(\cos \theta) \frac{2 n+1}{1+k_n} W_{n m} \times \\ {\left[\Delta C_{m m} \cos (m \lambda)+\Delta S_{m m} \sin (m \lambda)\right]} \end{gathered} $ | (1) |
式中,θ、λ分别表示地心余纬与经度;nmax为截断阶数,在本文中为60;R为地球平均半径;ρe和ρw分别表示地球平均密度和水密度;ΔCnm和ΔSnm为归一化球谐系数变化量;Pnm为n阶m次归一化缔合勒让德多项式;kn为n阶勒夫数;Wnm为n阶m次平滑核函数。
1.3 PnMl方法及其改进方法GRACE/GFO球谐系数模型在空间域具有明显的南北条带误差[10]。研究表明[3],条带误差与球谐系数的次相关误差模式有关。在以往研究中,为抑制该误差,Chen等[4]将PnMl(P4M6)方法应用于60阶次截断的GRACE球谐系数模型。
PnMl方法共有3个自由度,Nmin为球谐系数参与拟合部分的最低阶数,Nmax为球谐系数参与拟合部分的最高阶数,P表示用于拟合相关误差的多项式次数。数学模型如下:
| $ \Delta C_{nm}^{\mathrm{cor}}=\sum\limits_{i=0}^P\left(\sum\limits_{j=0}^P L_{i j}^{-1} \sum\limits_{k=N_{\min }}^{N_{\max }} k^j \Delta C_{k m}\right) n^i $ | (2) |
式中,ΔCnmcor为ΔCnm的相关误差;Ckm为k阶m次球谐系数(k=Nmin, Nmin+1, …, Nmax),k取奇数阶或偶数阶。同理可得ΔSnmcor表达式。其中Lij表达式为:
| $ L_{i j}=\sum\limits_{k=N_{\min }}^{N_{\max }} k^i k^j $ | (3) |
高次位系数的不足使全局保持拟合次数为P的多项式在接近nmax时难以拟合,导致应用60/96阶次截断(nmax=60/96)的GRACE/GFO时变重力场模型在经PnMl方法处理后,大于50/86阶次的位系数被完整保留(Nmax=50/86)[11]。未作处理的高阶次位系数表现为残余条带,严重污染经PnMl方法处理的反演结果。改进方法仍保持PnMl方法的3个自由度及其基本思想,对PnMl方法未作处理的高次球谐系数(Nmax, Nmax+1, …, nmax)采取分层拟合。以P4M6方法为例,未经改进时多项式拟合次数P在全局保持不变(P=4),经改进后多项式拟合次数P在不同层次的计算公式为:
| $ P=\left\{\begin{array}{l} p, N_{\min }<m \leqslant N_{\max } \\ p-1-\left(n-N_{\max }\right), \\ \quad N_{\max }<m \leqslant N_{\max }+p \\ 1, N_{\max }+p<m \leqslant n_{\max }-3 \end{array}\right. $ | (4) |
式中,Nmin为PnMl方法中位系数参与拟合部分的最低阶数,Nmax为PnMl方法中位系数参与拟合部分的最高阶数,nmax为截断阶数。p表示未经改进时在全局保持不变的多项式拟合次数,在改进方法中p=4。
1.4 信噪比评估采用海陆均方根之比定义信噪比指标[12],计算公式为:
| $ \mathrm{SNR}=\frac{\operatorname{RMS}(\text { Landsignal }+ \text { Noise })}{\operatorname{RMS}(\text { Oceansignal }+ \text { Noise })} $ | (5) |
式中,Noise代表噪声,Landsignal和Oceansignal分别代表陆地和海洋的真实质量信号。噪声水平(Noise)介于0和一个远大于陆地质量的正值之间,因此可以确定SNR取值范围在1~
广义三角帽方法假设不同观测序列包含相同的真实信号和相互独立的噪声。对任意给定格网点或区域,设Xi(t)(i=1, 2, 3)为三大机构GRACE/GFO时变重力场模型计算的陆地水储量变化时间序列,如
| $ \left\{\begin{array}{l} X_1(t)=Y(t)+\sigma_1(t) \\ X_2(t)=Y(t)+\sigma_2(t) \\ X_3(t)=Y(t)+\sigma_3(t) \end{array}\right. $ | (6) |
式中,Y(t)为真实地球质量变化信号,σi(t)为不同观测序列的独立噪声。进一步假设任意两个独立随机的观测值序列之和的方差等于两者方差之和,构造方差方程:
| $ \left\{\begin{array}{l} \operatorname{var}\left(\sigma_1\right)+\operatorname{var}\left(\sigma_2\right)=\operatorname{var}\left(X_1-X_2\right) \\ \operatorname{var}\left(\sigma_1\right)+\operatorname{var}\left(\sigma_3\right)=\operatorname{var}\left(X_1-X_3\right) \\ \operatorname{var}\left(\sigma_2\right)+\operatorname{var}\left(\sigma_3\right)=\operatorname{var}\left(X_2-X_3\right) \end{array}\right. $ | (7) |
若观测值序列中可用观测值个数为n,展开式(7)可得n(n-1)/2个方差方程。由于方差方程个数大于或等于观测数,每个观测值的噪声方差可以直接求解,或在n>3时通过最大平方求解。
2 结果与分析 2.1 空域分析以常用的P4M6方法为例,随机选取2007-11和2019-09的CSR模型进行测试,得到0.25°×0.25°全球质量变化(以EWH表示)(图 1),图中Gauss200表示半径为200 km的高斯滤波。原始时变重力场中存在显著的南北条带误差,经P4M6方法处理后反演结果有所改善(图 1(a)、(d)、(g)),但低纬度区域(30°S~30°N)仍存在残余条带。而改进方法可进一步有效抑制残余条带误差,即P4M6方法无法处理的高频分量中的噪声(图 1(b)、(h))。由差异图可知,改进方法可集中处理低纬度区域的条带误差(图 1(c)、(i))。对比传统方法可知,改进方法结合半径为200 km的高斯滤波可使反演结果更加清晰(图 1(e)、(f))。残余条带的减少使后续处理只需应用更弱的滤波策略便可得到清晰的反演结果,使潜在的地球物理信号得以被保留和揭示。

|
图 1 改进方法与P4M6方法在空域的表现与差异 Fig. 1 The performance and differences between improved method and P4M6 method in spatial domain |
为分析改进方法在频域的性能,采用2007-11的CSR模型计算60阶次球谐系数阶方差(图 2(a)),并给出不同处理方案的振幅及其差异(图 2(b)~(e))。原始高阶球谐系数的振幅出现较大异常值(图 2(b)),导致从25阶开始,原始阶方差呈现异常抬升变化(图 2(a))。经P4M6方法处理后阶方差的异常变化被抑制(图 2(c)),但较大的高阶信号阶方差会导致残余条带误差。而改进方法在50阶后的阶方差较P4M6方法有所下降,可去除高阶突变值(图 2(d)、(e))。

|
图 2 60阶次球谐系数阶方差和在不同处理策略下的振幅 Fig. 2 The degree variance and amplitude under different processing strategies of spherical harmonic coefficients with order 60 |
在空域和频域中,改进方法已被证明优于P4M6方法。为进一步比较2种方法在时域的性能,在全球范围内选取4个经典区域(3°×3°矩形质量块),矩形中心的大地坐标分别为(44.5°E,21.5°S)、(32.5°E,0.5°S)、(85.5°W,12.5°N)、(0°E,7.5°N),分别位于马达加斯加西南部、非洲维多利亚湖西北部、尼加拉瓜西北部、非洲沃特湖北部。
按式(1)计算得到矩形区域平均质量变化时间序列,并加入CSR-M作为可靠数据源计算矩形区域质量变化时间序列(图 3)。原始时间序列中的不合理峰值在采用P4M6方法后被部分移除,但仍存在残余突变值。而改进方法可进一步减少时间序列中的孤立异常值,使信号更符合季节性变化,且与CSR-M计算结果具有较好的一致性。
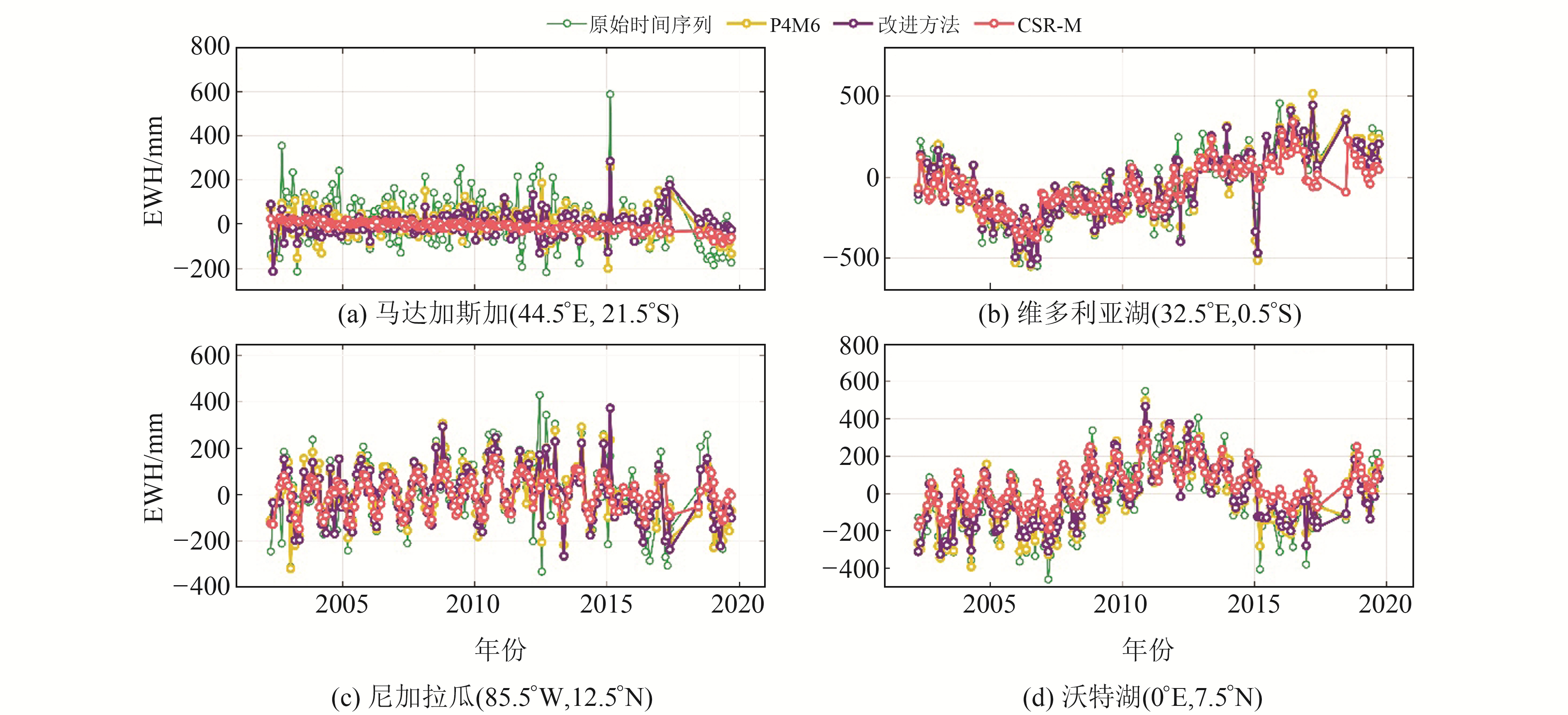
|
图 3 3°×3°矩形区域质量变化时间序列 Fig. 3 Time series of mass changes in 3°×3° rectangular area |
改进方法在空域、频域和时域的性能提升已被证明。为了量化改进方法去条带误差的效果,采用广义TCH计算三大机构模型以标准差(STD)表示的1°×1°全球不确定性格网评估改进方法,统计3组处理结果在全球及4个矩形区域的平均STD并计算SNR(图 4)。
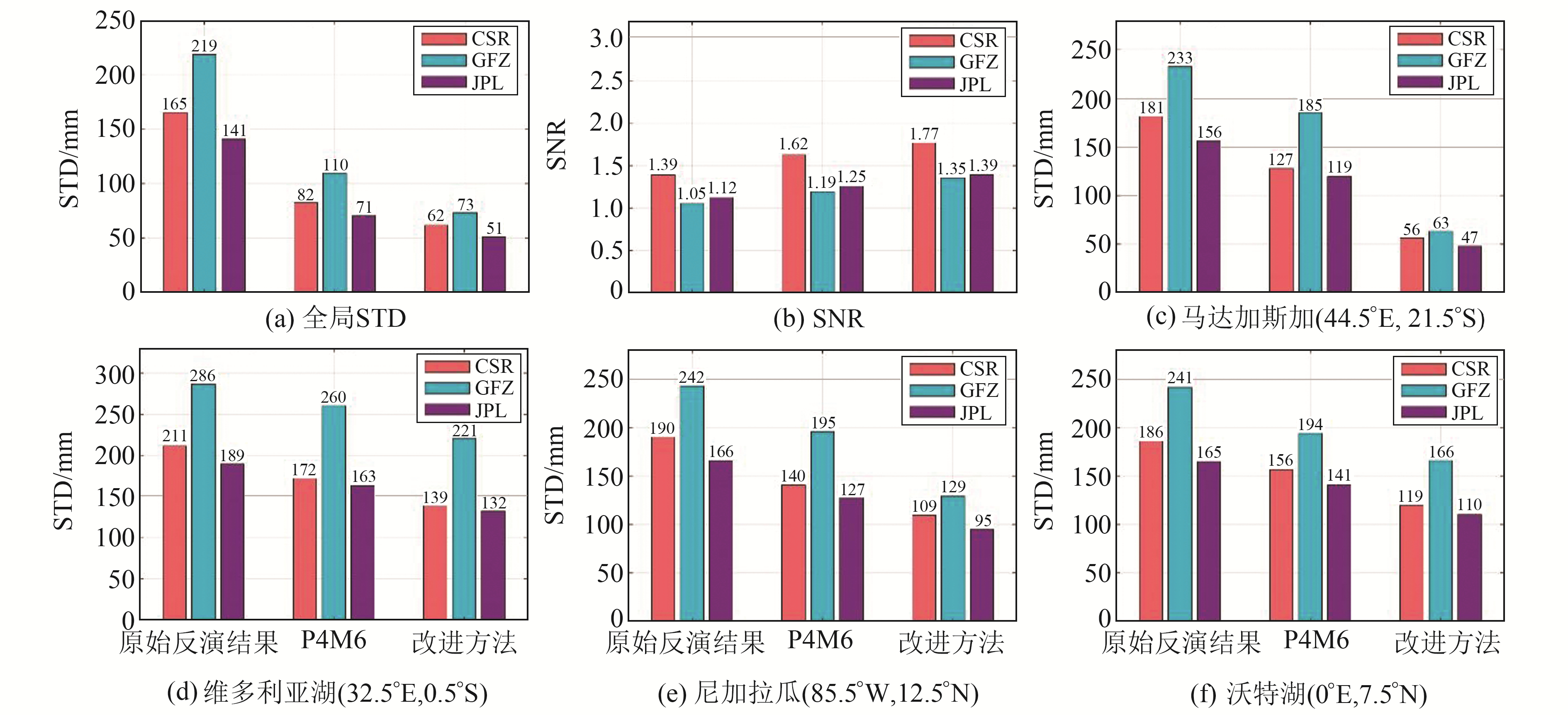
|
图 4 不同机构模型精度统计 Fig. 4 Error assessment of spherical harmonic coefficient released from different scientific data centers |
3种模型在采用改进方法后,全球及4个矩形区域的平均STD较P4M6方法均有所改善。在全球范围内,CSR、GFZ、JPL三种模型的平均STD分别下降20.50 mm、36.40 mm、19.61 mm(图 4(a)),表明改进方法可以进一步降低时变重力场模型的不确定性。此外,三者的SNR在采用改进方法后较P4M6方法分别从1.62、1.19、1.25增加到1.77、1.35、1.39(图 4(b))。
3 结语为处理GRACE/GFO时变重力场模型的条带噪声,本文提出一种改进的PnMl方法。该方法通过处理PnMl方法忽略的高次球谐系数,进一步抑制条带噪声。对比分析改进方法与常用的P4M6方法在空域、频域和时域的反演结果,同时采用广义TCH和SNR指标对该方法进行精度评定。主要结论如下:
1) 在空域中,改进方法可进一步抑制30°S~30°N区域的残余条带误差,使反演结果更加清晰。
2) 在频域中,改进方法可进一步抑制50阶后信号阶方差的异常抬升,减少高阶系数的阶方差突变值。
3) 在时域中,改进方法可进一步减少时间序列突变值,使信号更符合季节性变化。
4) 经统计,改进方法的SNR、全球和局部区域的平均STD均有明显改善。其中,CSR、GFZ、JPL三种模型结果在全球范围的平均STD分别下降20.50 mm、36.40 mm和19.61 mm,SNR从1.62、1.19、1.25增加至1.77、1.35、1.39。这表明,改进方法可通过进一步抑制条带误差来降低反演结果的不确定性。
| [1] |
Chambers D P. Evaluation of New GRACE Time-Variable Gravity Data over the Ocean[J]. Geophysical Research Letters, 2006, 33(17)
(  0) 0) |
| [2] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B12): 30 205-30 229 DOI:10.1029/98JB02844
(  0) 0) |
| [3] |
Swenson S, Wahr J. Post-Processing Removal of Correlated Errors in GRACE Data[J]. Geophysical Research Letters, 2006, 33(8)
(  0) 0) |
| [4] |
Chen J L, Wilson C R, Tapley B D, et al. Antarctic Regional Ice Loss Rates from GRACE[J]. Earth and Planetary Science Letters, 2008, 266(1-2): 140-148 DOI:10.1016/j.epsl.2007.10.057
(  0) 0) |
| [5] |
Swenson S, Chambers D, Wahr J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B8)
(  0) 0) |
| [6] |
Cheng M K, Tapley B D, Ries J C. Deceleration in the Earth's Oblateness[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(2): 740-747 DOI:10.1002/jgrb.50058
(  0) 0) |
| [7] |
Loomis B D, Rachlin K E, Wiese D N, et al. Replacing GRACE/GRACE-FO C30 with Satellite Laser Ranging: Impacts on Antarctic Ice Sheet Mass Change[J]. Geophysical Research Letters, 2020, 47(3)
(  0) 0) |
| [8] |
Peltier W R, Argus D F, Drummond R. Comment on "an Assessment of the ICE-6G_C(VM5a) Glacial Isostatic Adjustment Model" by Purcell et al[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(2): 2 019-2 028 DOI:10.1002/2016JB013844
(  0) 0) |
| [9] |
Save H, Bettadpur S, Tapley B D. High-Resolution CSR GRACE RL05 Mascons[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(10): 7 547-7 569 DOI:10.1002/2016JB013007
(  0) 0) |
| [10] |
Feng W. GRAMAT: A Comprehensive Matlab Toolbox for Estimating Global Mass Variations from GRACE Satellite Data[J]. Earth Science Informatics, 2019, 12(3): 389-404
(  0) 0) |
| [11] |
Yi S, Sneeuw N. A Novel Spatial Filter to Reduce North-South Striping Noise in GRACE Spherical Harmonic Coefficients[J]. Journal of Geodesy, 2022, 96(4)
(  0) 0) |
| [12] |
Chen J L, Wilson C R, Seo K W. Optimized Smoothing of Gravity Recovery and Climate Experiment(GRACE) Time-Variable Gravity Observations[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B6)
(  0) 0) |
2. Guangzhou Marine Geological Survey, CGS, 1133 Haibin Road, Guangzhou 511458, China
 2024, Vol. 44
2024, Vol. 44


