2. 防灾科技学院,河北省三河市学院街465号,065201;
3. 武汉引力与固体潮国家野外科学观测研究站,武汉市洪山侧路40号,430071
地球重力场随时间的变化可反映地球质量迁移、密度变化等多因素地球物理过程。超导重力仪是一种精密连续重力观测仪器,在精确观测重力潮汐信号的同时,也可记录到大气、海潮、极移及地震等引起的重力变化[1]。为了对重力观测数据进行处理与分析,需要识别和分离出各种地球物理信号。重力固体潮作为观测到的主要地球物理时变现象,其变化幅度可达200~500 μGal。在扣除理论重力固体潮效应后,全球尺度的观测残差主要受海潮和大气潮两大负荷源影响,而海潮和大气潮也会受到太阳、月亮等天体引潮力的作用,与固体潮具有相同的频率特征,无法直接从固体潮观测中有效分离[2-3]。因此,研究海潮和大气潮重力负荷效应有助于精确实施重力固体潮观测改正,为水文地质、地球内核震荡、地震预警等研究提供更为精确的数据。
本文基于布设在宜昌地震台的iGrav026超导重力仪在2017-01-01~12-31期间采集到的连续重力观测数据(图 1(a))和台站气压数据(图 1(b)),结合海潮模型、全球大气模型等资料,研究海潮和大气负荷产生的重力效应,从而对超导重力观测实施精密改正。

|
图 1 重力潮汐观测数据预处理 Fig. 1 Gravity tide observation data preprocessing |
使用Tsoft软件[4]对超导数据进行预处理。采用数字滤波方法将数据采样率由1 s降为1 min,利用“移去-恢复”技术修正数据。首先采用WDD模型[5]扣除理论固体潮(图 1(c)),然后采用经验大气导纳值扣除大气影响,导纳值取-3.0 nm·s-2·hPa-1。在残差数据上进行尖峰、间断、地震、阶跃等干扰的预处理。
1.2 极移改正由IAGBN绝对重力观测数据处理标准[6]可知,极移重力影响可表示为:
| $ \begin{array}{*{20}{c}} {\delta g=-1.164 \omega^2 a 2 \sin \varphi \cos \varphi}\\ {\left(x_p \cos \lambda-y_p \sin \lambda\right) \times 10^9} \end{array} $ | (1) |
式中,λ、φ分别表示测点经度、纬度;xp、yp分别表示2个地球自转参数;ω表示地球自转速度,取7.292 115×10-5 rad·s-1;a表示地球长半轴,取6 378 136 m。IERS(国际地球自转服务)网站已给出详尽的地球自转和极移参数,极移参数文件每天以数据形式给出,因此在计算得到极移重力效应序列后,通过样条插值得到与原始观测序列采样率相当的数据,结果如图 1(d)所示。经计算发现,在2017年内极移效应引起的重力变化最大可达约40 nm·s-2。
1.3 长周期趋势改正经过初步的理论重力固体潮、大气以及极移重力影响改正后,数据中存在一个长期升高趋势,可能与仪器漂移、水文负荷、地壳垂直位移和地球内部物质迁移有关[7],而这些因素在本文研究中为干扰项。为了尽量削弱该项影响,并避免过拟合造成的信息丢失,本文采用二次多项式方法[8-9]拟合重力长期趋势:
| $ d(t)=b_1+b_2 t+b_3 t^2 $ | (2) |
式中,b1、b2、b3分别表示趋势多项式的常数项、一次项系数和二次项系数。通过最小二乘拟合方法可以求解各项参数,计算获得的重力长期趋势如图 1(e)所示。
对预处理后的重力潮汐数据扣除极移重力影响和长周期趋势项,得到初步的重力残差(图 1(f))。由图可知,数据预处理效果较为理想,数据中残存较为明显的周期项,这可能与海潮或大气负荷有关。基于图 1(f)中残差数据,恢复先前扣除的理论固体潮和气压影响,再将数据降为1 h采样,作为调和分析的输入数据。
1.4 调和分析观测数据的调和分析是将观测信号分解为一系列周期性函数之和,求解各个潮波的潮汐特征参数(即振幅因子δ和相位滞后Δφ)并计算其估算精度的过程。振幅因子δ即各个潮波的观测振幅与理论振幅之比,为3个勒夫数的线性组合;相位滞后Δφ即各个潮波的实测相位与理论相位之差。Eterna[10]是使用最为广泛的调和分析软件,其主要原理是对观测数据使用最小二乘拟合估计潮汐参数。本文采用该软件对超导重力潮汐观测数据进行调和分析,结果见表 1。
|
|
表 1 宜昌台超导重力观测数据调和分析结果 Tab. 1 Harmonic analysis results of superconducting gravimetric observations at Yichang station |
海潮负荷计算首先从负荷格林函数理论[11]出发,通过将海潮潮高和负荷格林函数在球面进行褶积积分[12-13]得到海潮负荷,具体公式为:
| $ L_O(\theta, \lambda, t)=\rho_w \iint H\left(\theta^{\prime}, \lambda^{\prime}, t\right) G(\varphi, A) \mathrm{d} s $ | (3) |
式中,LO(θ, λ, t)为海潮负荷,θ、λ为计算点的余纬、经度;ρw为海水密度;H(θ′, λ′, t)为瞬时海潮潮高,θ′、λ′为海潮负荷点的余纬、经度;G(φ, A)为海潮重力格林函数,φ为负荷点至计算点的角距,A为负荷点至计算点的方向角;s为地球表面,ds为积分面元。
2.2 海潮负荷计算全球性或区域性海潮模型主要有FES、CSR、GOT、NAO、TPXO、EOT、DTU、HAMTIDE和OSU系列等[14]。其中,NAO.99b是日本国立天文台在2000年发布的海潮模型,采用同化模型方式构建,主要数据来源为T/P测高卫星以及日本验潮站资料,格网分辨率为0.5°[14];osu.Chinasea. 2010来自于俄勒冈州立大学,吸收了中国南海、台湾海峡和泰国湾等地区验潮站资料,在中国近海具有较高精度[15]。研究表明[16],NAO.99b模型在中国地区进行海潮改正是有效的。同时,为进一步提高海潮改正的效果,应结合中国近区海潮模型[13]。因此,本文结合全球NAO.99b模型与近区osu.Chinasea.2010模型,使用SPOTL软件[17]计算宜昌地震台海潮重力负荷效应。
表 2为采用上述海潮模型计算的周日、半日频段8个主要潮波重力负荷振幅。由表可知,在8个潮波中,K1波海潮重力负荷影响最大,幅值为4.142 nm·s-2;其次为O1波和M2波,幅值分别为3.735 nm·s-2和3.662 nm·s-2;其他潮波振幅均在2 nm·s-2以下,因此后续分析中重点考察K1、O1、M2三个主要潮波。从不同频段的影响来看,周日频段(O1、K1)的海潮负荷振幅大于半日频段(M2),这是由于宜昌台站地处中国南方,与区域性的海潮变化性质有关,这与孙和平等[18]的结论相符。
|
|
表 2 宜昌台海潮重力负荷计算结果 Tab. 2 Calculation results of ocean tide loading at Yichang station |
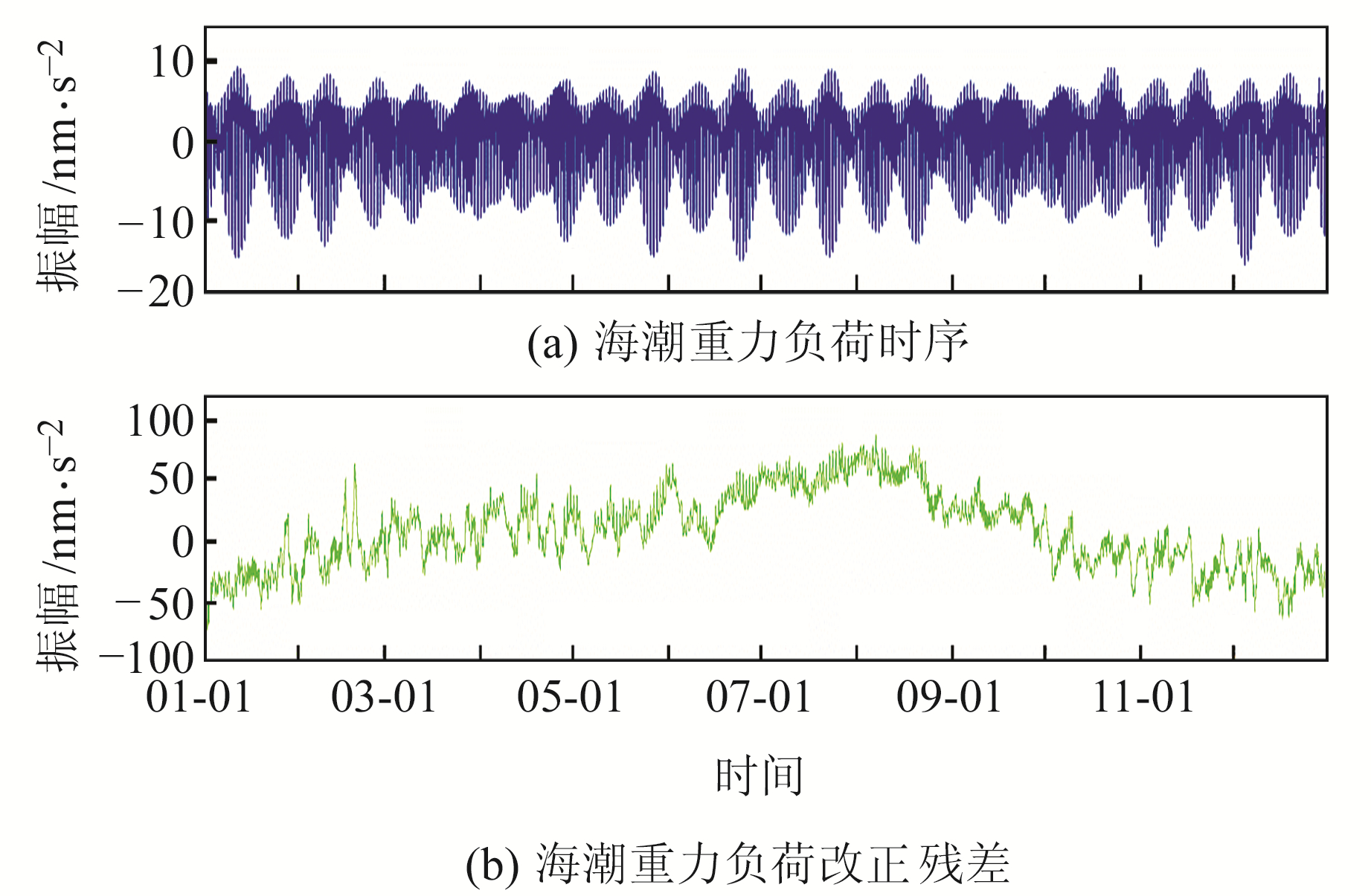
图 2(a)为通过上述模型计算的海潮重力负荷时序,可以看出,宜昌台海潮重力负荷周期性与理论固体潮(图 1(c))基本一致,最大变幅约为25 nm·s-2。图 2(b)为原始观测数据经过理论固体潮改正和海潮负荷改正的残差。
|
图 2 海潮重力负荷效应及改正 Fig. 2 Ocean tide gravity loading effects and its correction |
为了评价海潮负荷改正的效果,在对原始重力观测数据进行海潮负荷改正后,再次进行调和分析,改正前后的K1、O1、M2三个主要潮波潮汐因子如表 3所示。经海潮负荷改正后,O1、K1、M2潮波振幅因子分别减小1.2%、0.9%、0.6%;O1波相位滞后略有增大,K1、M2波相位滞后分别减小81.8%、24.6%。潮汐因子经海潮负荷改正后可构建实测固体潮模型,用于宜昌台精确重力固体潮改正。
|
|
表 3 海潮负荷改正前后O1、K1、M2波潮汐因子对比 Tab. 3 Comparison of O1, K1 and M2 wave tidal factors before and after ocean tide loading correction |
一般情况下,如果可以同时获取台站连续重力观测和同址气压观测数据,便可通过时域导纳方法进行气压改正。时域导纳方法就是将气压观测和重力残差时间序列作一元线性回归分析,获得时域大气重力导纳值[19]。分别对每月重力与气压观测序列进行回归分析,得到2017-01~12大气重力导纳值(表 4)。除1月、7月、8月、9月、10月外,其余7个月份相关系数基本在70%以上,取平均值得到导纳值为-3.219 3 nm·s-2·hPa-1,与经验导纳值较为接近。采用该导纳值计算气压重力负荷效应,结果如图 3(a)所示。由图可知,该方法计算的大气重力负荷影响在1 a内峰对峰振幅变化约为120 nm·s-2。
|
|
表 4 宜昌台2017年不同月份大气重力导纳值 Tab. 4 The monthly atmospheric gravity admittance factors at Yichang station |

|
图 3 大气重力负荷效应及改正 Fig. 3 Atmospheric gravity loading effects and its correction |
为了从重力潮汐观测中更精确地扣除大气重力信号,在考虑台站大气重力信号的同时,还需顾及全球性的大气重力效应[20]。本文选取全球大气模型来计算近区和远区大气重力效应。
3.2.1 大气负荷理论与海潮负荷计算类似,大气重力负荷效应计算也从负荷格林函数理论出发,通过对大气重力格林函数与全球大气数据进行褶积积分得到大气重力效应[21],具体公式为:
| $ L_P(\theta, \lambda, t)=\iint P\left(\theta^{\prime}, \lambda^{\prime}, t\right) G(\varphi) \mathrm{d} s $ | (4) |
式中,LP(θ, λ, t)为大气重力负荷,θ、λ为计算点的余纬、经度;P(θ′, λ′, t)为大气负荷点的大气压强,θ′、λ′为大气负荷点的余纬、经度;G(φ)为大气重力格林函数,φ为负荷点至计算点的角距;s为地球表面,ds为积分面元。
3.2.2 大气负荷计算本文选用的全球大气模型为ERA-Interim,由ECMWF(欧洲中期天气预报中心)发布(https://compreps.ecmwf.int/)。ERA-Interim再分析数据是在ERA40资料基础上,结合新的四维数据同化处理方法,应用更多卫星和地面观测资料,空间分辨率为0.75°×0.75°,最大时间分辨率是6 h。ERA-Interim模型包括垂向的37个气压位分层,由1 000 hPa上升至1 hPa(约37 km);数据时刻为00:00、06:00、12:00、18:00(UTC时间),其中00:00与12:00为分析数据,06:00和18:00为预报数据[22]。
选择0.5°为近区与远区分区阈值,基于ERA-Interim大气模型,计算得到2017-01~12期间宜昌地震台全球大气重力负荷效应,结果如图 3(b)所示。图中绿线为全球大气重力效应,包括远区大气重力效应(蓝线)和近区大气重力效应(红线)。计算结果显示,全球大气重力效应呈现季节性变化特点。气压主要受季节温度变化影响,春冬高、夏秋低,由于大气对重力的影响主要为负向吸引,因此重力效应呈现春冬低、夏秋高的特点,其1 a内峰对峰振幅变化约为80 nm·s-2。在全部影响中,近区大气重力效应占主要成分,其峰对峰幅值变化约为160 nm·s-2,且变化趋势与时域导纳法计算的大气重力效应基本一致,两者数值的差异反映出大气模型在局部地区精度存在欠缺;远区大气重力效应相对较小,变化趋势与近区重力效应呈负相关,在3~7月期间呈下降趋势,在8~11月期间呈上升趋势,其1 a内峰对峰幅值变化约为70 nm·s-2。
3.3 大气负荷改正原始观测数据在扣除海潮重力负荷效应和理论重力固体潮基础上,进一步扣除大气重力负荷效应。在对由大气重力导纳值计算的重力效应进行改正后,顾及到远区大气负荷影响,进一步使用大气模型计算的远区大气重力负荷效应进行改正,得到全球大气重力负荷改正结果,重力残差如图 3(c)所示。图中黑线为采用大气重力导纳值计算的重力效应进行改正的重力残差,在3~6月残差数据中存在幅值约40 nm·s-2的下降趋势;图中蓝线为考虑远区大气负荷的全球大气重力负荷改正残差。由前文计算结果可知,远区大气负荷在3~6月会引起负重力变化,在考虑该项因素后,残差数据中3~6月下降趋势得到有效改正。在最终重力残差结果中,1~2月变化趋势可能是由超导重力仪安装后的非线性零漂特征所致;6~10月呈现先上升后下降的趋势,变幅约为40 nm·s-2,该部分趋势变化主要反映陆地水[7]、地下水[23]等方面的影响。
4 结语本文对宜昌地震台超导重力观测中的海潮和大气重力负荷影响进行计算和分析,主要得到以下结论:
1) 宜昌台地处中国大陆中部,距离海岸线相对较远,海潮重力影响较小,海潮重力负荷最大变幅为25 nm·s-2,对于高精度的超导重力观测需要适当考虑海潮重力负荷的影响。在经过海潮负荷改正后,潮汐因子有一定改善。
2) 宜昌台大气时域导纳值为-3.219 3 nm·s-2·hPa-1,与经验值较为接近。通过理论计算发现,近区大气重力效应变幅达160 nm·s-2,为大气重力影响的主要部分;而远区大气重力效应变幅达70 nm·s-2,能够部分解释观测数据中的负重力变化。在进行超导重力观测数据精细化处理时,应考虑全球大气重力效应。
应当注意的是,超导重力仪在安装后可能出现非线性零漂,且长期零漂行为与开始安装时呈现不同的规律,而控制零漂的常用方法是与绝对重力仪进行同址观测[24]。对宜昌台超导重力仪进行绝对重力比对观测,获取精确格值并研究其长期漂移,是下一步将要开展的重点工作。
致谢: 感谢中国科学院精密测量科学与技术创新研究院陈晓东副研究员对本文内容和格式提出的建议和帮助。
| [1] |
陈晓东, 闫如玉, 牛晓伟, 等. 武汉台超导重力仪传递函数的测定[J]. 华中科技大学学报: 自然科学版, 2022, 50(9): 35-40 (Chen Xiaodong, Yan Ruyu, Niu Xiaowei, et al. Determination of Transfer Function for a Superconducting Gravimeter at Wuhan Station[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2022, 50(9): 35-40)
(  0) 0) |
| [2] |
许厚泽. 固体地球潮汐[M]. 武汉: 湖北科学技术出版社, 2010 (Xu Houze. Solid Earth Tides[M]. Wuhan: Hubei Science and Technology Press, 2010)
(  0) 0) |
| [3] |
Crossley D, Hinderer J, Riccardi U. The Measurement of Surface Gravity[J]. Reports on Progress in Physics, 2013, 76(4)
(  0) 0) |
| [4] |
Van Camp M, Vauterin P. Tsoft: Graphical and Interactive Software for the Analysis of Time Series and Earth Tides[J]. Computers and Geosciences, 2005, 31(5): 631-640 DOI:10.1016/j.cageo.2004.11.015
(  0) 0) |
| [5] |
Dehant V, Defraigne P, Wahr J M. Tides for a Convective Earth[J]. Journal of Geophysical Research: Solid Earth, 1999, 104(B1): 1 035-1 058 DOI:10.1029/1998JB900051
(  0) 0) |
| [6] |
王嘉沛, 张新林, 韩宇飞, 等. 2021年中国大陆构造环境监测网络绝对重力比测结果分析[J]. 华中科技大学学报: 自然科学版, 2022, 50(9): 11-16 (Wang Jiapei, Zhang Xinlin, Han Yufei, et al. Results of Comparison of Absolute Gravimeters from Crustal Movement Observation Network of China in 2021[J]. Journal of Huazhong University of Science and Technology : Natural Science Edition, 2022, 50(9): 11-16)
(  0) 0) |
| [7] |
韦进, 李辉, 刘子维, 等. 武汉九峰地震台超导重力仪观测分析研究[J]. 地球物理学报, 2012, 55(6): 1 894-1 902 (Wei Jin, Li Hui, Liu Ziwei, et al. Observation of Superconducting Gravimeter at Jiufeng Seismic Station[J]. Chinese Journal of Geophysics, 2012, 55(6): 1 894-1 902)
(  0) 0) |
| [8] |
陈晓东, 孙和平, 张为民, 等. 用绝对重力仪测定超导重力仪格值的精度分析[J]. 大地测量与地球动力学, 2013, 33(5): 145-149 (Chen Xiaodong, Sun Heping, Zhang Weimin, et al. Accuracy Analysis on Determination of Calibration Factor of a Superconducting Gravimeter Using an Absolute Gravimeter[J]. Journal of Geodesy and Geodynamics, 2013, 33(5): 145-149)
(  0) 0) |
| [9] |
牟丽爽, 冯金扬, 王启宇, 等. iGrav-012超导重力仪定期格值结果分析[J]. 计量学报, 2019, 40(3): 373-377 (Mou Lishuang, Feng Jinyang, Wang Qiyu, et al. Analysis of Calibration Factor of Superconducting Gravimeter iGrav-012[J]. Acta Metrologica Sinica, 2019, 40(3): 373-377 DOI:10.3969/j.issn.1000-1158.2019.03.04)
(  0) 0) |
| [10] |
Wenzel H G. The Nanogal Software: Earth Tide Data Processing Package ETERNA 3.30[J]. Bulletin d'Informations Marees Terrestres, 1996, 124: 9 425-9 439
(  0) 0) |
| [11] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797 DOI:10.1029/RG010i003p00761
(  0) 0) |
| [12] |
Agnew D C. NLOADF: A Program for Computing Ocean-Tide Loading[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5 109-5 110 DOI:10.1029/96JB03458
(  0) 0) |
| [13] |
杜文成, 袁林果, 张宁宁, 等. 青岛台站重力固体潮和海潮负荷特征研究[J]. 大地测量与地球动力学, 2018, 38(9): 913-916 (Du Wencheng, Yuan Linguo, Zhang Ningning, et al. Study of Earth's Gravity Tide and Oceanic Loading Characteristics at Qingdao Station[J]. Journal of Geodesy and Geodynamics, 2018, 38(9): 913-916)
(  0) 0) |
| [14] |
张胜凯, 雷锦韬, 李斐. 全球海潮模型研究进展[J]. 地球科学进展, 2015, 30(5): 579-588 (Zhang Shengkai, Lei Jintao, Li Fei. Advances in Global Ocean Tide Models[J]. Advances in Earth Science, 2015, 30(5): 579-588)
(  0) 0) |
| [15] |
范文蓝, 姜卫平, 袁林果, 等. 不同海潮模型对中国沿海区域海潮负荷位移改正影响分析[J]. 大地测量与地球动力学, 2018, 38(6): 598-602 (Fan Wenlan, Jiang Weiping, Yuan Linguo, et al. Effects of Different Ocean Tide Models on OTL Correction in China's Coastal Areas[J]. Journal of Geodesy and Geodynamics, 2018, 38(6): 598-602)
(  0) 0) |
| [16] |
李盛, 胡久常, 周雯, 等. 琼中台重力非潮汐变化气压与海潮负荷改正[J]. 中国地震, 2022, 38(1): 102-111 (Li Sheng, Hu Jiuchang, Zhou Wen, et al. The Air Pressure and Ocean Tide Correction of Gravity Non-Tidal Changes in Qiongzhong Seismic Station[J]. Earthquake Research in China, 2022, 38(1): 102-111 DOI:10.3969/j.issn.1001-4683.2022.01.010)
(  0) 0) |
| [17] |
Agnew D C. SPOTL: Some Programs for Ocean-Tide Loading[R]. Scripps Institution of Oceanography Technical Report, San Diego, 2012
(  0) 0) |
| [18] |
孙和平, 周江存, 许厚泽. 中国地壳运动观测网络基准站倾斜固体潮观测中的海潮负荷信号改正问题[J]. 地球物理学进展, 2001, 16(3): 31-39 (Sun Heping, Zhou Jiangcun, Xu Houze. Correction Problem of the Ocean Loading Signals on Tilt Measurements at Fundamental Stations in Crust Movement Observation Network in China[J]. Progress in Geophysics, 2001, 16(3): 31-39 DOI:10.3969/j.issn.1004-2903.2001.03.004)
(  0) 0) |
| [19] |
陈晓东. 武汉九峰台超导重力仪固体潮观测资料的预处理和分析结果[D]. 武汉: 中国科学院测量与地球物理研究所, 2003 (Chen Xiaodong. Preprocessing and Analytical Results of the Tidal Gravity Observations Recorded with a Superconducting Gravimeter at Jiufeng Station, Wuhan[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2003)
(  0) 0) |
| [20] |
徐建桥, 郝兴华, 孙和平. 武汉基准台气压对重力潮汐观测的影响[J]. 测绘学报, 1999, 28(1): 21-27 (Xu Jianqiao, Hao Xinghua, Sun Heping. Influence of Atmospheric Pressure on Tidal Gravity at Wuhan Station[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1): 21-27 DOI:10.3321/j.issn:1001-1595.1999.01.005)
(  0) 0) |
| [21] |
张敏. 重力测量的环境影响研究[D]. 北京: 中国地震局地球物理研究所, 2021 (Zhang Min. Environmental Impact Analysis of Gravity Measurement[D]. Beijing: Institute of Geophysics, CEA, 2021)
(  0) 0) |
| [22] |
王郁茗, 邵利民, 张尚悦. 利用ERA-Interim数据构建海区大气加权平均温度模型[J]. 气象科学, 2020, 40(3): 408-413 (Wang Yuming, Shao Limin, Zhang Shangyue. Building Atmospheric Weighted Average Temperature Model for Sea Area Using ERA-Interim Data[J]. Journal of the Meteorological Sciences, 2020, 40(3): 408-413)
(  0) 0) |
| [23] |
贺前钱, 罗少聪, 孙和平, 等. 武汉九峰站地下水变化对重力场观测的影响[J]. 地球物理学报, 2016, 59(8): 2 765-2 772 (He Qianqian, Luo Shaocong, Sun Heping, et al. The Influence of Groundwater Changes on Gravity Observations at Jiufeng Station in Wuhan[J]. Chinese Journal of Geophysics, 2016, 59(8): 2 765-2 772)
(  0) 0) |
| [24] |
邢乐林, 李辉, 刘子维, 等. 利用绝对重力测量精密测定超导重力仪的格值因子[J]. 大地测量与地球动力学, 2010, 30(1): 48-50 (Xing Lelin, Li Hui, Liu Ziwei, et al. Scale Factor Calibration of a Superconducting Gravimeter by Using Absolute Gravimetry[J]. Journal of Geodesy and Geodynamics, 2010, 30(1): 48-50)
(  0) 0) |
2. Institute of Disaster Prevention, 465 Xueyuan Street, Sanhe 065201, China;
3. Wuhan Gravitation and Solid Earth Tides, National Observation and Research Station, 40 Hongshance Road, Wuhan 430071, China
 2024, Vol. 44
2024, Vol. 44


