通过重力密度反演分析技术可以更准确地了解地质体结构、形状及其他特征,为此,国内外学者进行大量工作。Li等[1-2]引入深度加权函数;Portniaguine等[3]引入最小梯度支撑函数约束重力反演;Chasseriau等[4]提出基于随机方法的反演技术;Zhdanov[5]提出重磁反演和成像新方法;Commer[6]提出深度分辨率增强的加权方案;耿美霞等[7]建立在密度约束下的多变量协同克里金联合反演方程;张志厚等[8]提出一种基于深度学习的重力异常及重力梯度异常的联合反演方法。
在三维密度反演领域已经存在诸多算法,但可用于密度反演的公开软件却很少。基于此,本文借助MATLAB语言,开发一个支持三维密度反演、重力场正演、数据分析及可视化等功能的系统软件,为重力三维密度反演学习和研究提供软件工具支持。
1 方法原理 1.1 重力场正演根据牛顿万有引力定律,由计算点体积质量密度元素产生的万有引力势为[9]:
| $ V(P)=G \iiint\limits_V \frac{\rho}{r} \mathrm{~d} V $ | (1) |
式中,G为牛顿万有引力常数;ρ为质量密度;r=
| $ V\left(\boldsymbol{r}_i\right)=G \sum\limits_{j=1}^M \rho_j \int\limits_{\Delta V_j} \frac{1}{\boldsymbol{r}-\boldsymbol{r}_i} \mathrm{~d} V $ | (2) |
式中,r为径向矢量;ΔVj为第j个棱柱体的体积;ρj为第j个棱柱体的密度;M为长方体总数。本文采用Nagy等[10]推导的位、引力矢量和引力梯度张量表达式用于重力场正演计算。
1.2 三维密度反演根据待求解密度模型的特点建立合适的反演目标函数:
| $ S=\varphi_d+\mu \varphi_m $ | (3) |
式中,φd为数据拟合项。通常认为重力数据观测噪声符合高斯分布特点,因而采用L2范数进行构建:
| $ \varphi_d=\left\|\boldsymbol{W}_d\left(\boldsymbol{d}^{\text {obs }}-\boldsymbol{d}^{\text {pre }}\right)\right\|_2^2 $ | (4) |
式中,Wd为每个数据点的权重方阵;dobs为观测数据点的N×1维向量;dpre为预测数据点的N×1维向量。模型拟合项定义如下:
| $ \varphi_m(\boldsymbol{\rho})=\left(\boldsymbol{\rho}-\boldsymbol{\rho}_0\right)^{\mathrm{T}}\left(\sum\limits_{i=s, x, y, z} \boldsymbol{W}_i^{\mathrm{T}} \boldsymbol{W}_i\right)\left(\boldsymbol{\rho}-\boldsymbol{\rho}_0\right) $ | (5) |
式中,ρ0为模型参考密度值;Wi=αiSiDiZ(i=s, x, y, z),其中αi为权重系数,Ss为每个单元格所占权重,Sx, y, z为各自方向每个边缘处所占权重,Ds为对角线上数值为
| $ \boldsymbol{w}(z)=\frac{1}{\left(z_0+z\right)^{\beta / 2}} $ | (6) |
式中,z0为观测高度;z为单元深度;β为拟合指数项。因此,目标函数可表示为:
| $ \varphi(\boldsymbol{\rho})=\varphi(\boldsymbol{p})_d+\mu \varphi_m(\boldsymbol{p}) $ | (7) |
最后,通过最小二乘可得:
| $ \begin{gathered} \boldsymbol{\rho}=\boldsymbol{\rho}_0+\left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{W}_d^{\mathrm{T}} \boldsymbol{W}_d \boldsymbol{G}+\mu \boldsymbol{W}_m^{\mathrm{T}} \boldsymbol{W}_m\right)^{-1} \\ \boldsymbol{G}^{\mathrm{T}} \boldsymbol{W}_d^{\mathrm{T}} \boldsymbol{W}_d\left(\boldsymbol{d}_{\mathrm{obs}}-\boldsymbol{G} \boldsymbol{\rho}_0\right) \end{gathered} $ | (8) |
本文软件是基于Windows10系统,开发环境为Intel(R) Core(TM) i5-9300H CPU,8G内存。系统结构和操作流程如图 1所示。该软件由三维密度反演和数据结果界面两部分组成(图 2),主要功能包括参数设置、地下模型空间划分、重力观测数据选择、反演结果显示与预测。
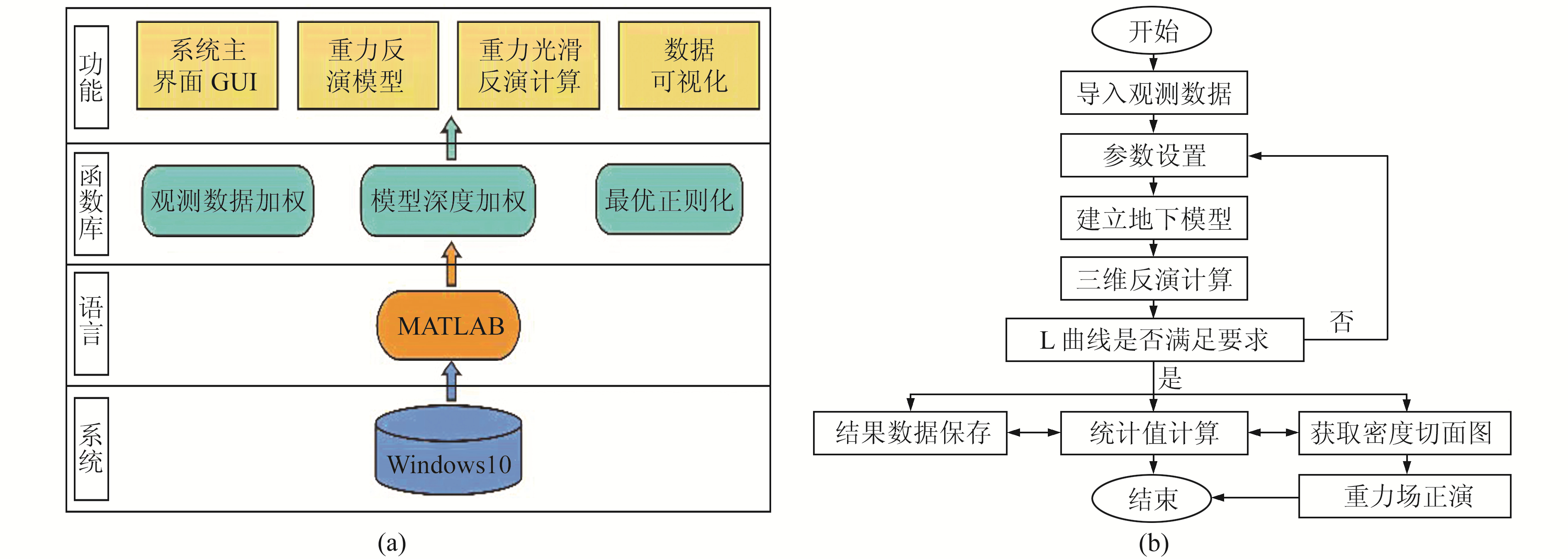
|
图 1 系统设计框架与操作流程 Fig. 1 System design framework and operation process |

|
图 2 三维密度反演主界面与子界面 Fig. 2 The main interface and sub-interface of three-dimensional density inversion |
测区范围为1 000 m×1 000 m×500 m,网格划分为20×20×10,单模型x轴范围为400~600 m,y轴范围为400~600 m,z轴范围为100~300 m,密度为1 g/cm3。模型切面及观测数据如图 3所示,反演结果如图 4所示。
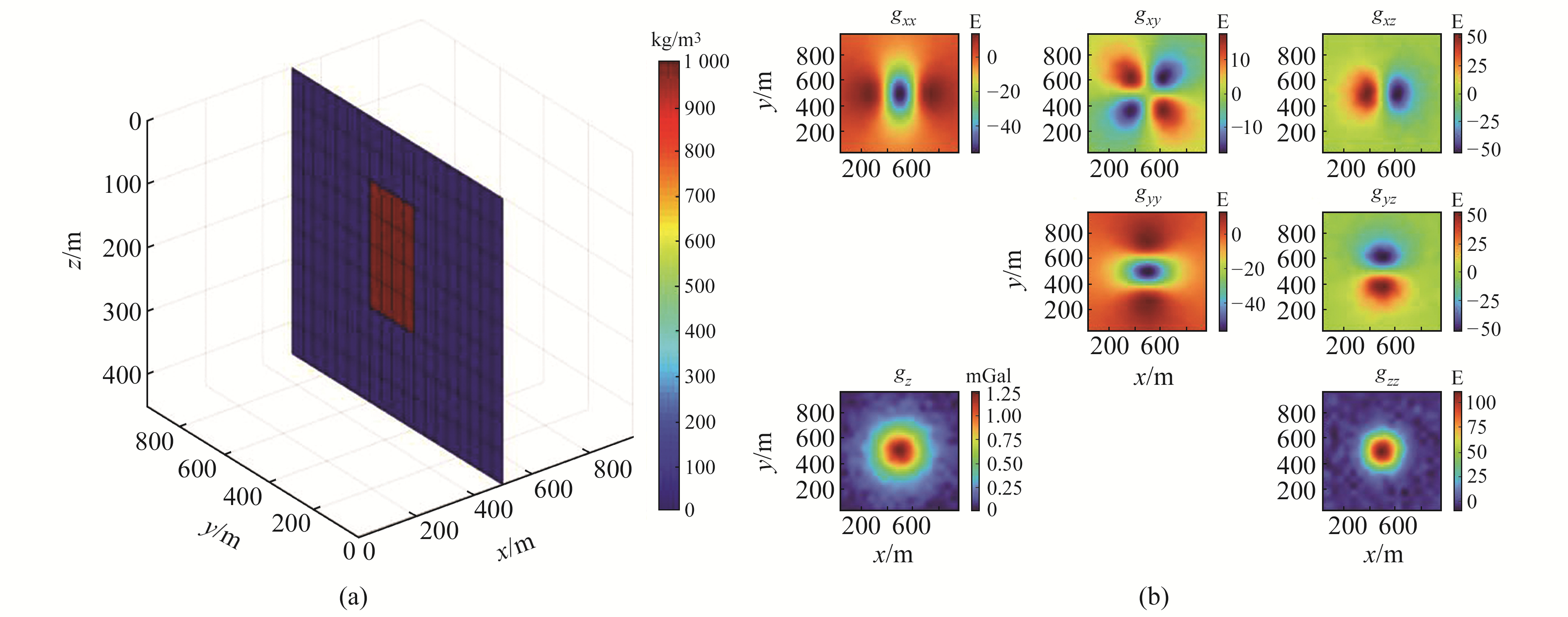
|
图 3 模型切面与重力观测数据 Fig. 3 Model profile and gravity observation data |
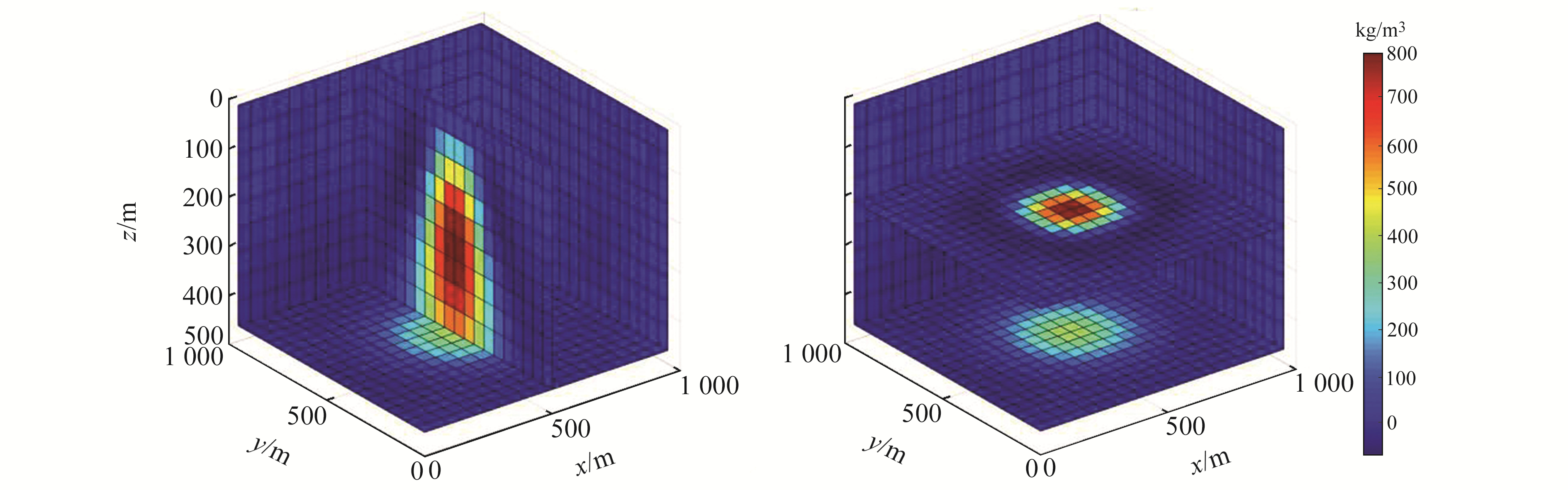
|
图 4 反演模型在x=500 m、z=200 m处密度切面 Fig. 4 Density profiles of inversion model at x=500 m and z=200 m |
从图 4可以看出,反演结果能够有效地反映地质体的空间分布,验证了本文软件的有效性。
3.2 实测数据测试本文采用文顿盐丘(Vinton Dome)地区重力梯度实测数据进行反演测试。文顿盐丘位于美国墨西哥湾沿岸,该地区岩盖密度约为2.75 g/cm3,盐丘附近沉积物、围岩及盐核密度均约为2.2 g/cm3,即岩盖剩余密度约为0.55 g/cm3。本文选用的测区范围为4 000 m×4 000 m×1 000 m,网格划分为40×40×20。
图 5为实测重力梯度gzz和预测gzz数据,由图可知,预测数据与实测数据拟合效果较好。图 6为密度反演结果,从图中可以看出,反演密度集中部分顶部埋深约为200 m,底部埋深约为600 m。该结果与前人研究所得埋深结果200~650 m[11]、200~550 m[12]较为接近,验证了软件的可靠性与实用性。
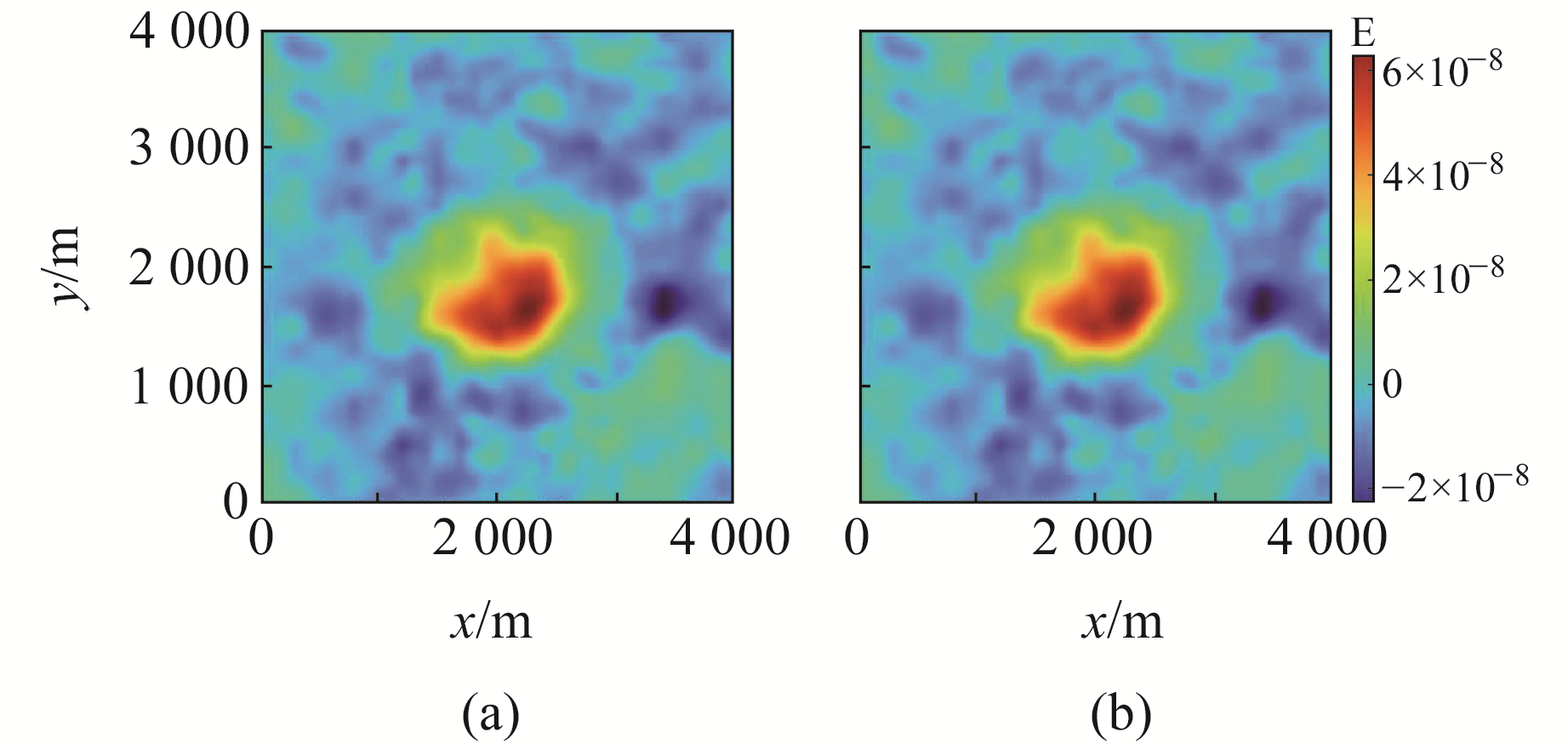
|
图 5 实测重力梯度数据与密度异常体预测数据 Fig. 5 Measured gravity gradient data and predicted density anomaly data |

|
图 6 反演模型在y=2 000 m、z=300 m和z=700 m处密度切面 Fig. 6 Density profiles of inversion model at y=2 000 m, z=300 m and z=700 m |
本文开发出一个重力三维密度光滑反演软件,具有最优正则化参数选取、数据文件管理、密度反演计算及结果分析和可视化等功能。模拟和实测数据测试结果验证了该软件的有效性与实用性,未来可以在计算效率等方面进一步优化。
| [1] |
Li Y G, Oldenburg D W. 3-D Inversion of Magnetic Data[J]. Geophysics, 1996, 61(2): 394-408 DOI:10.1190/1.1443968
(  0) 0) |
| [2] |
Li Y G, Oldenburg D W. 3-D Inversion of Gravity Data[J]. Geophysics, 1998, 63(1): 109-119 DOI:10.1190/1.1444302
(  0) 0) |
| [3] |
Portniaguine O, Zhdanov M S. Focusing Geophysical Inversion Images[J]. Geophysics, 1999, 64(3): 874-887 DOI:10.1190/1.1444596
(  0) 0) |
| [4] |
Chasseriau P, Chouteau M. 3D Gravity Inversion Using a Model of Parameter Covariance[J]. Journal of Applied Geophysics, 2003, 52(1): 59-74 DOI:10.1016/S0926-9851(02)00240-9
(  0) 0) |
| [5] |
Zhdanov M S. New Advances in Regularized Inversion of Gravity and Electromagnetic Data[J]. Geophysical Prospecting, 2009, 57(4): 463-478 DOI:10.1111/j.1365-2478.2008.00763.x
(  0) 0) |
| [6] |
Commer M. Three-Dimensional Gravity Modelling and Focusing Inversion Using Rectangular Meshes[J]. Geophysical Prospecting, 2011, 59(5): 966-979 DOI:10.1111/j.1365-2478.2011.00969.x
(  0) 0) |
| [7] |
耿美霞, 黄大年, 于平, 等. 基于协同克里金方法的重力梯度全张量三维约束反演[J]. 地球物理学报, 2016, 59(5): 1 849-1 860 (Geng Meixia, Huang Danian, Yu Ping, et al. Three-Dimensional Constrained Inversion of Full Tensor Gradiometer Data Based on Cokriging Method[J]. Chinese Journal of Geophysics, 2016, 59(5): 1 849-1 860)
(  0) 0) |
| [8] |
张志厚, 廖晓龙, 曹云勇, 等. 基于深度学习的重力异常与重力梯度异常联合反演[J]. 地球物理学报, 2021, 64(4): 1 435-1 452 (Zhang Zhihou, Liao Xiaolong, Cao Yunyong, et al. Joint Gravity and Gravity Gradient Inversion Based on Deep Learning[J]. Chinese Journal of Geophysics, 2021, 64(4): 1 435-1 452)
(  0) 0) |
| [9] |
Heiskanen W A, Moritz H. Physical Geodesy[M]. San Francisco: Freeman and Company, 1967
(  0) 0) |
| [10] |
Nagy D, Papp G, Benedek J. The Gravitational Potential and Its Derivatives for the Prism[J]. Journal of Geodesy, 2000, 74(7-8): 552-560 DOI:10.1007/s001900000116
(  0) 0) |
| [11] |
Geng M X, Huang D N, Yang Q J, et al. 3D Inversion of Airborne Gravity-Gradiometry Data Using Cokriging[J]. Geophysics, 2014, 79(4): 37-47 DOI:10.1190/geo2013-0393.1
(  0) 0) |
| [12] |
Qin P B, Huang D N, Yuan Y, et al. Integrated Gravity and Gravity Gradient 3D Inversion Using the Non-Linear Conjugate Gradient[J]. Journal of Applied Geophysics, 2016, 126: 52-73 DOI:10.1016/j.jappgeo.2016.01.013
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44


