2. 新疆维吾尔自治区地质矿产勘查开发局地球物理化学探矿大队,新疆维吾尔自治区昌吉市延安南路119号,831100;
3. 新疆维吾尔自治区地质矿产勘查开发局第八地质大队,新疆维吾尔自治区阿克苏市北京路55号,843000;
4. 中国地质大学(武汉)地球物理与空间信息学院地球内部多尺度成像湖北省重点实验室,武汉市鲁磨路388号,430074
天山地区构造运动活跃,晚古生代时期,在西伯利亚和塔里木地块碰撞作用下,准噶尔、吐哈、博格达、哈尔里克等多个块体拼贴增生,形成近东西向的天山造山带(图 1)。天山造山带属于典型的新生代复活型造山带,其基本格架形成于古生代晚期[1]。新生代时期,受印度板块碰撞与俯冲欧亚大陆的远程效应影响,塔里木地块向北俯冲挤压天山,致使天山造山带复活隆升,形成天山地区现今的大型盆山相间格局[2]。板块碰撞和俯冲强烈改造了天山及相邻盆地的岩石圈结构,GPS水平垂向观测数据显示[3],天山造山带当前仍处于整体隆升状态,而塔里木盆地则表现为下沉趋势。为了更好地研究天山地区的岩石圈演化和形变过程,仍需要更多证据。

|
图 1 天山地区地形与构造单元示意图 Fig. 1 The schematic diagram of topography and tectonic units of the Tianshan area |
地形是研究岩石圈形变最直接的地球物理观测量之一,可刻画不同构造单元的地表特征。然而,即使是在活跃的和最新的地质构造区域,地形仍被岩石圈密度差异极大地均衡补偿[4],使得研究各种动力学作用对岩石圈形变的影响变得困难。一种有效的方法是首先从观测地形中扣除岩石圈均衡贡献的部分,得到剩余地形[5];然后从剩余地形中滤波扣除其中的长波长部分(如地幔对流),得到中短波长部分(也称作均衡剩余地形)[6],其可反映其他各种构造运动(如碰撞和俯冲作用)对地形的贡献,有助于了解岩石圈形变过程。本文基于岩石圈挠曲均衡理论,考虑有效弹性厚度的变化,计算研究区均衡剩余地形。首先联合重力、地震横波速度和莫霍面数据,反演岩石圈剩余密度结构,然后结合有效弹性厚度和地形数据计算均衡剩余地形,最后讨论天山地区的均衡剩余地形特征及其对岩石圈形变的启示。
1 方法理论剩余地形包含两部分,分别为长波长部分的动力剩余地形(也称动力地形)和中短波长部分的均衡剩余地形[6]。为了得到均衡剩余地形,首先需要计算剩余地形。根据前人研究中对剩余地形的定义[5],可从观测地形中扣除岩石圈均衡贡献的部分后得到。在Airy均衡情况下,即假设岩石圈有效弹性厚度为0,剩余地形可表示为[6-7]:
| $ \begin{gathered} H_{\text {res }}=\frac{1}{\rho_{\text {res }}} \rho_{\text {top }} H_{\text {obs }}+ \\ \frac{1}{\rho_{\text {res }}} \int_0^z \Delta \rho(z)\left(\frac{R-z}{R}\right)^2 \mathrm{~d} z \end{gathered} $ | (1) |
式中,ρtop为观测地形Hobs的改正密度,在陆地通常设置为2 670 kg·m-3;ρres为剩余地形Hres的平均密度,设置为2 670 kg·m-3;Δρ(z)为岩石圈内部的密度异常,z为大地水准面以下岩石圈深度;Z为积分深度;R为地球平均半径。
然而,上述计算忽略了岩石圈的有效弹性厚度。尽管在研究长波长部分的动力剩余地形时,其可以忽略,但对中短波长部分的均衡剩余地形而言,有效弹性厚度的变化至关重要。根据岩石圈具有的滤波器(Q)特性[8],式(1)可以进一步写为:
| $ \begin{gathered} H_{\text {res }}=\left(\frac{1}{\rho_{\text {res }}} \rho_{\text {top }} H_{\text {obs }}+\right. \\ \left.\frac{1}{\rho_{\text {res }}} \int_0^Z \Delta \rho(z)\left(\frac{R-z}{R}\right)^2 \mathrm{~d} z\right) Q \end{gathered} $ | (2) |
由于岩石圈有效弹性厚度通常为变量,因此在荷载ρH作用下,滤波器Q通常描述为一个四阶偏微分方程[9]:
| $ \begin{gathered} D \nabla^2 \nabla^2 H_{\text {output }}+2 \frac{\partial D}{\partial x} \frac{\partial}{\partial x} \nabla^2 H_{\text {output }}+ \\ 2 \frac{\partial D}{\partial y} \frac{\partial}{\partial y} \nabla^2 H_{\text {output }}+\nabla^2 D \nabla^2 H_{\text {output }}-(1-v) \\ \left(\frac{\partial^2 D}{\partial^2 x} \frac{\partial^2 H_{\text {output }}}{\partial^2 y}-2 \frac{\partial^2 D}{\partial x \partial y} \frac{\partial^2 H_{\text {output }}}{\partial x \partial y}+\right. \\ \left.\frac{\partial^2 D}{\partial^2 y} \frac{\partial^2 H_{\text {output }}}{\partial^2 x}\right)+\rho_{\text {output }} g H_{\text {output }}=\rho_{\text {input }} g H_{\text {input }} \end{gathered} $ | (3) |
式中,ρinput和ρoutput分别为等效输入地形Hinput和输出地形Houtput的密度,在本研究中均设置为2 670 kg·m-3,与剩余地形密度相同;▽2为拉普拉斯算子;g为重力加速度;D=ETe3/[12(1-v2)]为挠曲刚度,E为杨氏模量,Te为有效弹性厚度,v为泊松比。表 1为本文使用的所有参数,偏微分方程(3)通过有限差分方法求解。
|
|
表 1 本研究所用参数 Tab. 1 The parameters used in this paper |
本文采用联合反演方法,利用布格重力异常、地震横波速度和莫霍面数据得到研究区岩石圈密度异常。研究区初始重力数据(图 2(a))是基于地球重力场模型EIGEN-6C4得到,观测面高度为10 km。地形重力效应是基于ETOPO1全球高程/水深模型,采用球冠体积分的重力异常正演方法[10]计算166.7 km范围地形产生的10 km高度重力效应(图 2(b))。从自由空间重力异常中扣除地形产生的重力效应,得到研究区布格重力异常(图 2(c))。

|
图 2 天山地区重力异常及地形重力效应 Fig. 2 Gravity anomalies and topographic gravity effects of the Tianshan area |
利用地震横波速度和莫霍面数据构建岩石圈(0~150 km)初始密度异常模型。地震数据采用Lü等[11]针对天山地区研究获得的地壳-上地幔横波速度结构,该模型具有较高的水平分辨率,约为0.5°~0.75°。莫霍面深度数据来自Stolk等[12]发布的亚洲地壳模型,该模型由地震数据获得,在研究区具有较高的分辨率,约为1°×1°。基于上述数据,将地震横波速度转换为初始地壳密度[13]。对于地幔部分,将横波速度异常转换为地幔密度异常[14],其与平均地幔密度3 270 kg·m-3之和被设置为初始地幔密度。对于参考密度模型,通常的做法是采用平均莫霍面深度或正常地壳厚度30 km作为划分均匀水平层状地壳和地幔之间的参考深度(也称作补偿深度)。张星宇等[15]根据均衡理论研究显示,天山地区补偿深度最佳值约为39 km。因此,本文将划分地壳和地幔的参考深度设置为39 km,初始密度模型与参考密度模型之差即为初始密度异常模型。本文使用Audet等[16]基于Fan小波谱分析方法计算得到的有效弹性厚度模型。
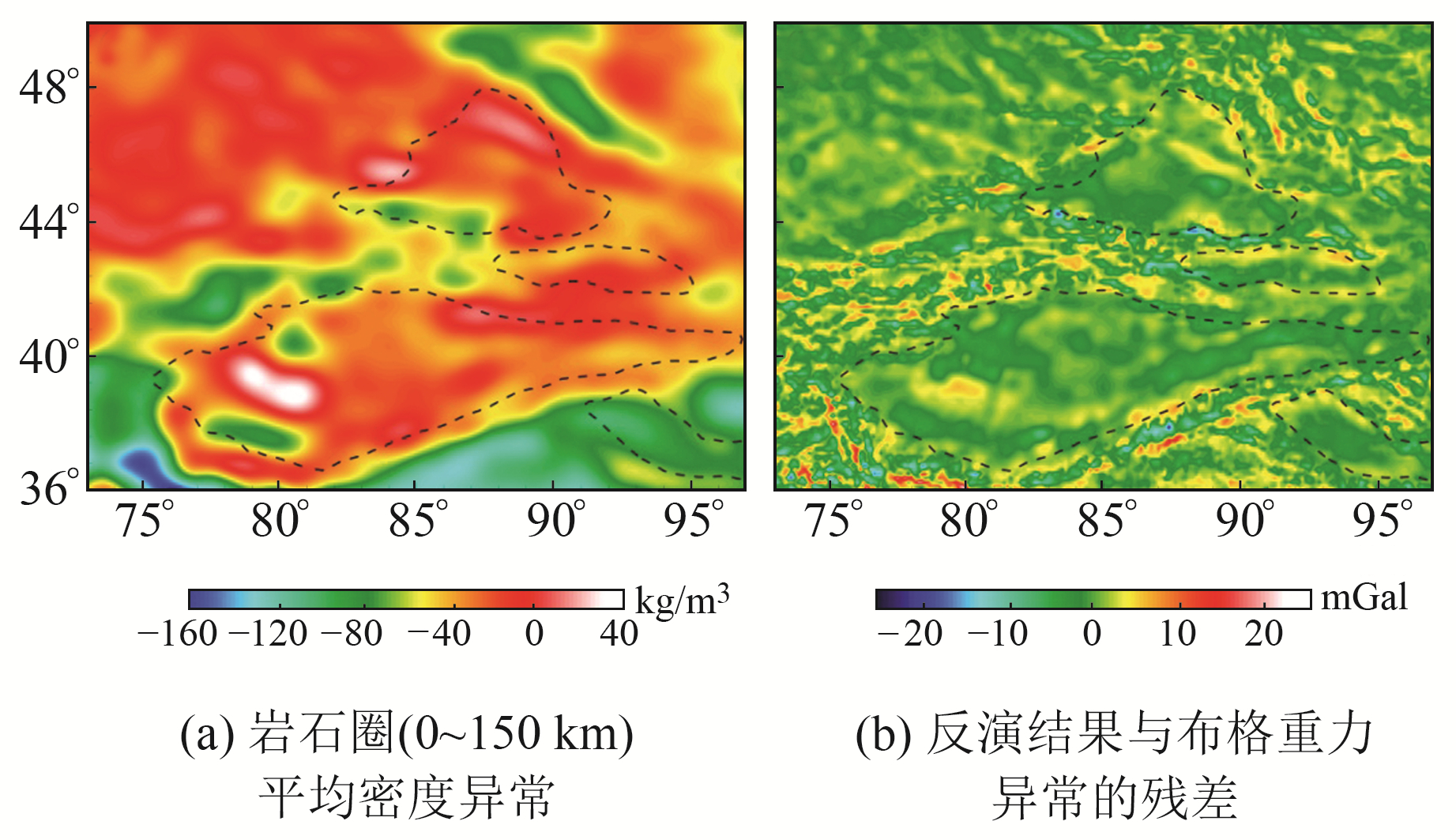
根据布格重力异常和初始密度异常模型,采用联合反演方法[17]获得最终的岩石圈密度异常结构(图 3(a))。为了验证反演结果的可靠性,对反演得到的岩石圈密度异常结构进行正演计算,并将正演得到的重力异常与输入的布格重力异常(图 2(c))作差,结果如图 3(b)所示。从图中可以看出,拟合差幅值整体较小,基本在±10 mGal以内。
|
图 3 岩石圈密度异常 Fig. 3 Density anomalies of the lithosphere |
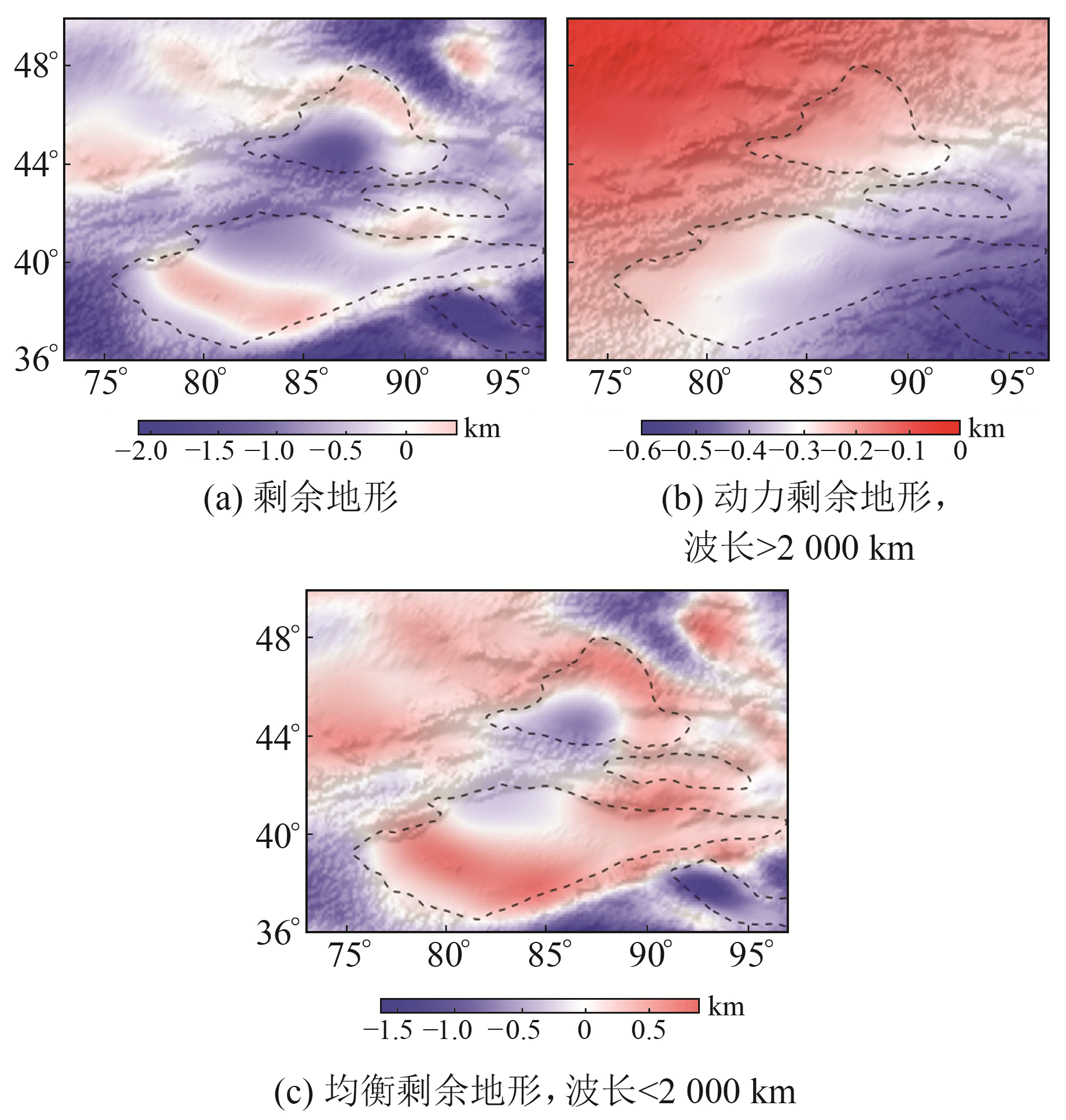
基于反演获得的岩石圈密度异常结构,结合研究区有效弹性厚度模型,利用式(2)和(3)即可计算得到天山地区剩余地形(图 4(a))。为了消除边界效应的影响,挠曲计算向外扩展574 km,即假设有效弹性厚度为70 km时第一挠曲节点[8]的距离。同时,为了减小地球曲率的影响,本文采用兰勃特圆锥保角投影进行有限差分的挠曲计算。从图 4(a)可以看出,剩余地形结果仍然受到显著的长波长动力影响(如地幔对流)。Kaban等[7]通过对全球剩余地形和均衡重力异常进行球谐分析,发现球谐阶次小于20阶的部分(对应波长大于2 000 km)能较好地指示深部地幔对流信号。Flament等[5]同样将剩余地形中波长大于2 000 km的部分用来讨论全球尺度的地幔对流过程。因此,为了更好地研究岩石圈尺度的形变特征,本文将剩余地形中波长大于2 000 km的部分(图 4(b))进行高斯滤波扣除,得到中短波长部分的均衡剩余地形,结果如图 4(c)所示。
|
图 4 天山地区剩余地形 Fig. 4 Residual topography of the Tianshan area |
由图 4可知,研究区均衡剩余地形与构造单元具有良好的对应性。负值主要出现在年轻造山带,如天山中部和西部、阿尔泰山、青藏高原等,最低可达-1.6 km。正值则主要出现在部分老块体,如塔里木盆地、吐哈盆地、准噶尔盆地北部、哈萨克斯坦块体等,最高可达0.9 km。其中,天山西部和中部显示出大片负值,且西部幅值较低,约为-0.2~0 km,中部幅值较高,约为-0.5~0 km,而东部(>88°E)则基本为较低幅值的正值,约为0~0.3 km。相比之下,阿尔泰山均衡剩余地形负值较低,最低值约为-0.9 km,青藏高原负值最低,极小值约为-1.6 km。另外,塔里木盆地北缘中部和准噶尔盆地南部虽然显示出局部负值,但塔里木盆地整体为大片正值,极大值约为0.9 km,准噶尔盆地北部同样显示出大片正值,最大值约为0.8 km。研究区西北部的哈萨克斯坦块体基本为正值,约为0~0.6 km,而吐哈盆地均衡剩余地形正值较低,不超过0.4 km。
3.2 均衡剩余地形对岩石圈形变的启示通常在无外力扰动情况下,由于地形被岩石圈密度差异均衡补偿,均衡剩余地形应当趋近于0,全球大范围的低值均衡重力异常[18]也可证实该特征。然而,这在构造活跃的地区往往并不成立,板块碰撞、俯冲等过程导致岩石圈发生形变,造成额外的地形。研究区均衡剩余地形的剧烈变化表明,该地区曾经经历复杂的构造运动。
自新生代以来,印度板块与欧亚大陆持续发生剧烈碰撞,其远程效应波及整个天山地区。GPS水平观测数据显示[19],天山地壳当前仍处于持续缩短状态,且自西向东地壳缩短速率逐渐减小,西部可达20 mm/a,东部仅约1 mm/a。在刚性塔里木块体的碰撞和俯冲作用下,天山不仅复活隆升,且发生更为剧烈的下地壳增厚,形成天山中西部(< 88°E)负值均衡剩余地形。相比之下,天山西部(约74°~80°E)均衡剩余地形幅值略小于天山中部(80°~88°E),这可能与软流圈上涌有关。地震横波速度结果显示[11],天山西部存在明显的软流圈上涌,可能会贡献部分正地形,在一定程度上抵消下地壳剧烈增厚所形成的负值均衡剩余地形。此外,根据地震波速度结构可知,天山东部(>88°E)并无明显的增厚山根,表明岩石圈形变主要以地表抬升为主,并形成正值均衡剩余地形。由图 4(c)可知,天山中西部均衡剩余地形幅值小于阿尔泰山和青藏高原,这可能与岩石圈强度有关。天山岩石圈有效弹性厚度较高,表明天山块体整体具有较高的力学强度,在板块碰撞和挤压过程中,岩石圈形变相对较小。而与区内造山带形成显著对比的是,塔里木盆地、吐哈盆地和哈萨克斯坦等块体基本为正值均衡剩余地形,地质上通常认为塔里木盆地是具有前寒武陆壳基底的稳定地块,而哈萨克斯坦块体同样被认为是相对稳定的克拉通,这些说明在板块碰撞和挤压过程中,相对较老的刚性块体整体发生抬升。
4 结语本文根据挠曲均衡理论,首先采用联合重力和地震数据反演方法,获得天山地区岩石圈密度异常结构;然后考虑岩石圈有效弹性厚度的横向变化,采用有限差分方法,计算得到研究区均衡剩余地形。得到以下认识:
1) 天山地区显示出复杂的均衡剩余地形特征,且与各构造单元具有良好的对应性,不同块体的均衡剩余地形幅值均较高,表明研究区中新生代以来经历了复杂的演化过程。
2) 区内山脉(天山中西部、阿尔泰山和青藏高原)主要为负值均衡剩余地形,而塔里木盆地、吐哈盆地和哈萨克斯坦等较老块体主要为正值均衡剩余地形。这说明在板块碰撞和挤压过程中,较老块体岩石圈整体发生抬升,而年轻造山带岩石圈形变主要表现为地表抬升和更为剧烈的下地壳增厚。
3) 天山各段均衡剩余地形存在差异,中部(80°~88°E)和西部(约74°~80°E)基本为负值,反映出俯冲导致的下地壳增厚,且西部幅值相对较小,可能与软流圈上涌有关;而天山东部(>88°E)则为低幅值的正值,表明岩石圈形变主要以地表抬升为主。
| [1] |
肖序常, 汤耀庆, 李锦轶, 等. 试论新疆北部大地构造演化[J]. 新疆地质科学, 1990(1): 47-68 (Xiao Xuchang, Tang Yaoqing, Li Jinyi, et al. On the Tectonic Evolution of the Northern Xinjiang, Northwest China[J]. Geoscience of Xinjiang, 1990(1): 47-68)
(  0) 0) |
| [2] |
Molnar P, Tapponnier P. Cenozoic Tectonics of Asia: Effects of a Continental Collision: Features of Recent Continental Tectonics in Asia can be Interpreted as Results of the India-Eurasia Collision[J]. Science, 1975, 189(4 201): 419-426
(  0) 0) |
| [3] |
Pan Y J, Hammond W C, Ding H, et al. GPS Imaging of Vertical Bedrock Displacements: Quantification of Two-Dimensional Vertical Crustal Deformation in China[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(4)
(  0) 0) |
| [4] |
Mooney W D, Laske G, Masters T G. CRUST 5.1: A Global Crustal Model at 5°×5°[J]. Journal of Geophysical Research: Solid Earth, 1998, 103 (B1): 727-747
(  0) 0) |
| [5] |
Flament N, Gurnis M, Müller R D. A Review of Observations and Models of Dynamic Topography[J]. Lithosphere, 2013, 5(2): 189-210 DOI:10.1130/L245.1
(  0) 0) |
| [6] |
Kaban M K, Schwintzer P, Artemieva I M, et al. Density of the Continental Roots: Compositional and Thermal Contributions[J]. Earth and Planetary Science Letters, 2003, 209(1-2): 53-69 DOI:10.1016/S0012-821X(03)00072-4
(  0) 0) |
| [7] |
Kaban M K, Schwintzer P, Reigber C. A New Isostatic Model of the Lithosphere and Gravity Field[J]. Journal of Geodesy, 2004, 78(6): 368-385 DOI:10.1007/s00190-004-0401-6
(  0) 0) |
| [8] |
Watts A B. Isostasy and Flexure of the Lithosphere[M]. Cambridge: Cambridge University Press, 2001
(  0) 0) |
| [9] |
Stark C P, Stewart J, Ebinger C J. Wavelet Transform Mapping of Effective Elastic Thickness and Plate Loading: Validation Using Synthetic Data and Application to the Study of Southern African Tectonics[J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B12)
(  0) 0) |
| [10] |
Heck B, Seitz K. A Comparison of the Tesseroid, Prism and Point-Mass Approaches for Mass Reductions in Gravity Field Modelling[J]. Journal of Geodesy, 2007, 81(2): 121-136 DOI:10.1007/s00190-006-0094-0
(  0) 0) |
| [11] |
Lü Z Q, Gao H Y, Lei J S, et al. Crustal and Upper Mantle Structure of the Tien Shan Orogenic Belt from Full-Wave Ambient Noise Tomography[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(4): 3 987-4 000 DOI:10.1029/2019JB017387
(  0) 0) |
| [12] |
Stolk W, Kaban M, Beekman F, et al. High Resolution Regional Crustal Models from Irregularly Distributed Data: Application to Asia and Adjacent Areas[J]. Tectonophysics, 2013, 602: 55-68 DOI:10.1016/j.tecto.2013.01.022
(  0) 0) |
| [13] |
Brocher T M. Empirical Relations between Elastic Wavespeeds and Density in the Earth's Crust[J]. Bulletin of the Seismological Society of America, 2005, 95(6): 2 081-2 092 DOI:10.1785/0120050077
(  0) 0) |
| [14] |
Levandowski W, Boyd O S, Briggs R W, et al. A Random-Walk Algorithm for Modeling Lithospheric Density and the Role of Body Forces in the Evolution of the Midcontinent Rift[J]. Geochemistry Geophysics Geosystems, 2015, 16(12): 4 084-4 107 DOI:10.1002/2015GC005961
(  0) 0) |
| [15] |
张星宇, 陈超, 杜劲松, 等. 天山及邻区Vening Meinesz均衡重力异常特征及其动力学意义[J]. 地球物理学报, 2020, 63(10): 3 791-3 803 (Zhang Xingyu, Chen Chao, Du Jinsong, et al. Characteristics of Vening Meinesz Isostatic Gravity Anomalies in Tien Shan and Surroundings and Its Dynamic Significances[J]. Chinese Journal of Geophysics, 2020, 63(10): 3 791-3 803)
(  0) 0) |
| [16] |
Audet P, Bürgmann R. Dominant Role of Tectonic Inheritance in Supercontinent Cycles[J]. Nature Geoscience, 2011, 4(3): 184-187 DOI:10.1038/ngeo1080
(  0) 0) |
| [17] |
Liang Q, Chen C, Li Y G. 3-D Inversion of Gravity Data in Spherical Coordinates with Application to the GRAIL Data[J]. Journal of Geophysical Research: Planets, 2014, 119(6): 1 359-1 373 DOI:10.1002/2014JE004626
(  0) 0) |
| [18] |
Balmino G, Vales N, Bonvalot S, et al. Spherical Harmonic Modelling to Ultra-High Degree of Bouguer and Isostatic Anomalies[J]. Journal of Geodesy, 2012, 86(7): 499-520 DOI:10.1007/s00190-011-0533-4
(  0) 0) |
| [19] |
Wang Q, Zhang P Z, Freymueller J T, et al. Present-Day Crustal Deformation in China Constrained by Global Positioning System Measurements[J]. Science, 2001, 294(5 542): 574-577
(  0) 0) |
2. Geophysical and Geochemical Prospecting Brigade, Geology and Mineral Exploration and Development Bureau of Xinjiang Uygur Autonomous Region, 119 South-Yan'an Road, Changji 831100, China;
3. The Eight Geological Brigade, Geology and Mineral Exploration and Development Bureau of Xinjiang Uygur Autonomous Region, 55 Beijing Road, Aksu 843000, China;
4. Hubei Subsurface Multi-Scale Imaging Key Laboratory, School of Geophysics and Geomatics, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China
 2024, Vol. 44
2024, Vol. 44


