2. 安徽理工大学空间信息与测绘工程学院,安徽省淮南市泰丰大街168号,232001
星载原子钟作为GNSS导航卫星的重要载荷之一,维持着导航系统星上时间基准,其性能决定着导航卫星在轨服务寿命与精密单点定位(PPP)精度。卫星钟差通过GFZ、WHU等数据分析中心发布,其采样间隔为900 s、300 s、30 s。然而在实际应用中,接收机采样间隔为30 s、15 s、10 s、1 s甚至更低。观测数据不能满历元对应钟差产品历元,因此钟差产品无法满足实际应用需求,需要将卫星钟差产品进行建模加密,获得与实际观测值相同或更小采样间隔的卫星钟差数据[1]。
为获取更加连续和精确的钟差改正值,需要使用内插或拟合方法对钟差产品进行加密。目前,国内外常用的卫星钟差建模加密算法有[2-3]:线性插值(linear interpolation)、拉格朗日插值(Lagrange polynomial interpolation)、切比雪夫拟合(Chebyshev polynomial fitting)、最小二乘多项式拟合(least squares polynomial fitting)等。本文在最小二乘多项式拟合基础上,提出附加L1范数正则项(Lasso),并采用滑动建模方法,即滑动Lasso拟合法建立参数稀疏的GNSS瞬时钟差模型。使用GFZ提供的精密钟差产品,将滑动Lasso拟合法与滑动拉格朗日插值、滑动切比雪夫拟合、滑动最小二乘多项式拟合等3种常用的钟差建模加密算法进行卫星钟差拟合精度及PPP定位精度对比。
1 稀疏模型构建稀疏模型的建立是在利用最小二乘多项式构建卫星钟差模型时附加L1范数正则项,减少卫星钟差数据中的误差,以增加偏差的方式来减少方差,抑制钟差模型过拟合,达到约束模型参数和去除次要变量的目的[4]。
1.1 Lasso拟合算法Lasso算法函数表达式为:
| $ \begin{gathered} \boldsymbol{W}=\operatorname{argmin}_W\left\{(\boldsymbol{Y}-\boldsymbol{X} \boldsymbol{W})^{\mathrm{T}} \boldsymbol{P}(\boldsymbol{Y}-\boldsymbol{X} \boldsymbol{W})+\right. \\ \left.\alpha\left\|\boldsymbol{w}_j\right\|_1\right\} \end{gathered} $ | (1) |
式中,W为瞬时钟差模型的参数矩阵;Y为真实钟差值;α为正则化参数;‖ wj‖1为W的L1范数。
本文使用快速迭代收缩阈值算法(FISTA)对Lasso进行求解,其表达式为:
| $ \boldsymbol{W}_{k+1}=S\left(\boldsymbol{\psi}_k-\frac{\boldsymbol{X}^{\mathrm{T}}\left(\boldsymbol{X} \boldsymbol{\psi}_k-\boldsymbol{Y}\right)}{L}, \frac{\lambda}{L}\right) $ | (2) |
式中,S(, )为软阈值算子;ψk为Nestrerov加速迭代回归参数。令
| $ f(\boldsymbol{W})=(\boldsymbol{Y}-\boldsymbol{X} \boldsymbol{W})^{\mathrm{T}} \boldsymbol{P}(\boldsymbol{Y}-\boldsymbol{X} \boldsymbol{W}) $ | (3) |
| $ g(\boldsymbol{W})=\alpha\left\|\boldsymbol{w}_j\right\|_1 $ | (4) |
使用梯度下降法求解f(W),其中f(W)梯度计算使用2阶泰勒展开式,忽略常数项,近端迭代式为:
| $ \begin{gathered} \boldsymbol{W}_k=\operatorname{argmin} \\ \left\{\frac{L}{2}\left\|\boldsymbol{W}-\left(\boldsymbol{W}_{k-1}-\frac{1}{\mathrm{eig}_{\max }\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}\right)} \nabla f\left(\boldsymbol{W}_{k-1}\right)\right)\right\|_2^2+\right. \\ \left.\lambda\|\boldsymbol{W}\|_1+\text { const }\right\} \end{gathered} $ | (5) |
设置Nestrerov加速项,ψk为Wk-1和Wk-2的线性组合,tk为组合权重因子,则:
| $ \boldsymbol{\psi}_k=\boldsymbol{W}_{k-1}+\frac{t_k-1}{t_k}\left(\boldsymbol{W}_{k-1}-\boldsymbol{W}_{k-2}\right) $ | (6) |
| $ t_k=\frac{1+\sqrt{1+4 t_{k-1}^2}}{2} \quad\left(t_1=1\right) $ | (7) |
将ψk代替Wk-1代入式(5)可得到式(1)解算的参数迭代式,若ψk-Wk小于设定的阈值或达到最大迭代次数,则返回拟合模型的系数向量。钟差拟合模型的正则化参数选取通过K折交叉验证(K-fold CV)来确定。研究表明[5],10折交叉验证能够更好地确定钟差模型拟合的正则化参数。
1.2 滑动Lasso拟合算法滑动Lasso拟合算法通过不断变换拟合区域,令需要加密的区间始终处于钟差拟合精度较高区域的中心。因此,使用滑动式方法建模加密能够提高模型精度,大大减少拟合模型边缘区域误差较大的问题[6]。
2 实验分析为验证滑动Lasso拟合算法在钟差模型拟合中的精度及有效性,使用德国地学研究中心(GFZ) 2020-06-29~07-01发布的300 s采样间隔的GBM精密钟差产品进行卫星钟差拟合精度与PPP定位精度分析。
2.1 钟差数据预处理在进行钟差建模前,需要对钟差数据进行预处理,去除大部分粗差以及钟跳[7]。本文采用中位数偏差法(MAD)进行钟差数据异常检测,公式如下:
| $ \operatorname{MAD}=\operatorname{Median}\left\{\frac{\left|y_i-m\right|}{0.6745}\right\} $ | (8) |
式中,m=Median{yi},yi为时钟频率数据;当|yi|>(m+n*MAD)时,则认为该数据为异常数据,需将其去除,本文n值取3可以较好地去除钟差异常数据[8]。通过对钟差数据进行预处理,可以减小异常数据的影响,提高钟差数据的稳定性。
2.2 卫星钟差拟合精度分析通过滑动Lasso拟合、滑动拉格朗日插值、滑动切比雪夫拟合、滑动最小二乘多项式拟合对300 s钟差数据进行加密得到30 s钟差数据。将GFZ发布的30 s精密钟差产品作为真值,采用均方根误差作为拟合精度指标,比较各算法的拟合精度。考虑到各卫星系统及不同类型原子钟对钟差插值建模的影响[9],选取卫星如表 1所示,各算法的拟合精度如图 1和表 2(单位ns)所示。
|
|
表 1 选取的卫星统计 Tab. 1 Statistics of the selected satellites |

|
图 1 各算法钟差拟合精度 Fig. 1 Clock offset fitting accuracy of each algorithm |
|
|
表 2 各算法平均拟合精度统计 Tab. 2 Statistics of average fitting accuracy of each algorithm |
通过图 1和表 2可以看出,滑动Lasso拟合在BDS、GPS卫星上的精度有所提高,在GLONASS卫星上的拟合精度略微低于其他算法,在Galileo卫星上的拟合精度低于滑动拉格朗日插值和滑动最小二乘多项式拟合,高于滑动切比雪夫拟合。为更明显地体现滑动Lasso拟合与其他算法的差异,以G01卫星钟差数据预处理后第210~250历元数据为例,钟差频率如图 2所示。图中红线为钟差频率中值线,红点为变化较大但未被预处理剔除的点。对该时间段各算法的插值结果进行分析(表 3)。
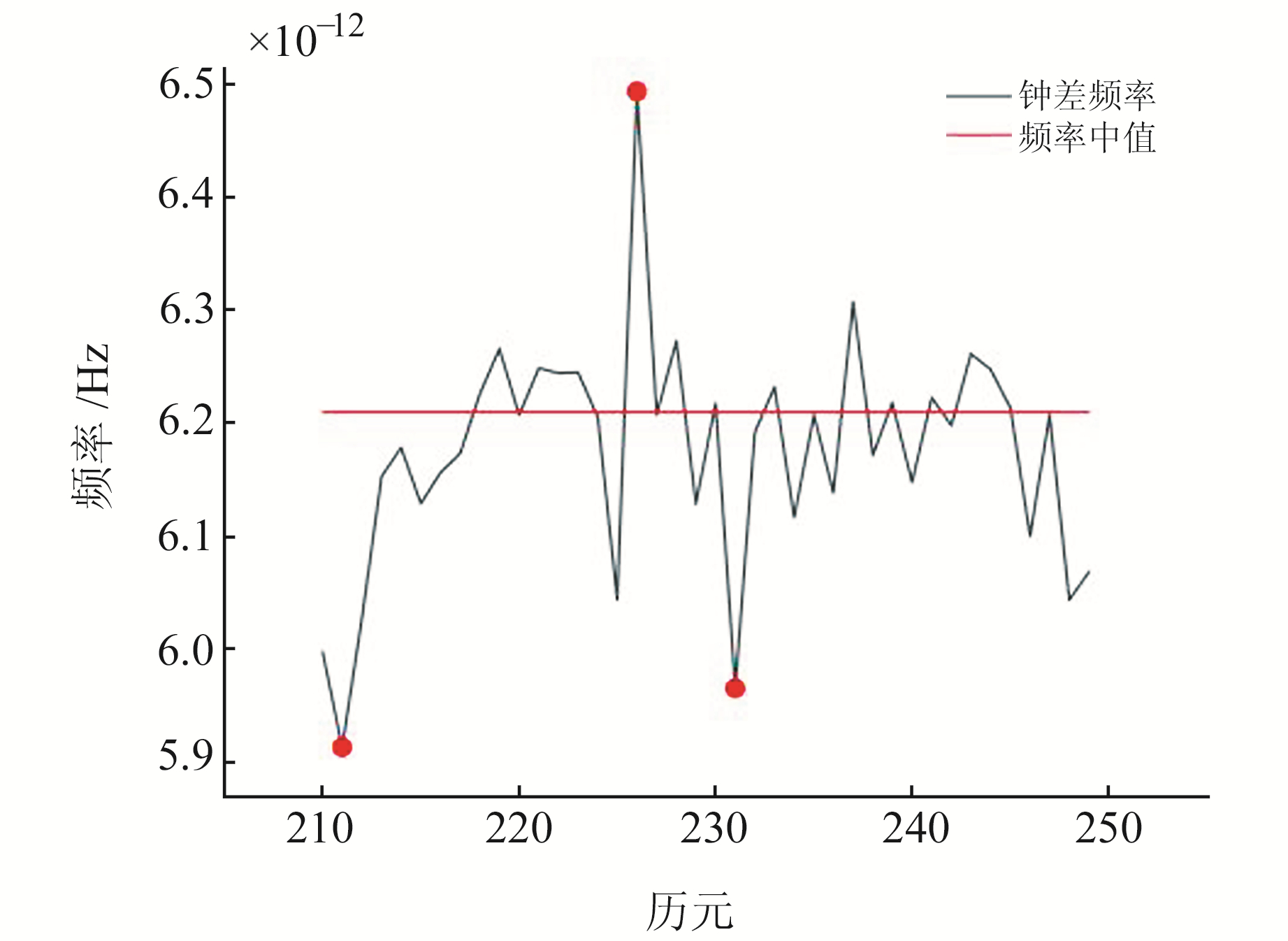
|
图 2 G01卫星部分钟差频率 Fig. 2 Partial clock offset frequency of G01 satellite |
|
|
表 3 滑动Lasso拟合法精度提高率统计 Tab. 3 Statistics of accuracy improvement rate of sliding Lasso fitting method |
综上可知,当局部钟差变化较大时,Lasso算法相较于其他3种算法能很好地降低异常钟差数据对钟差拟合模型的影响,提高模型拟合精度。此外,滑动Lasso算法在拟合铷钟钟差时精度最高,氢钟钟差拟合精度次之,铯钟钟差拟合精度最差。其原因为铯钟噪声相比于铷钟更为平滑,发生局部跳变的现象更少[10]。因此,在原子钟噪声较大和局部跳变更为频繁时,滑动Lasso拟合法能够更好地防止钟差拟合模型出现过拟合现象。
2.3 定位精度比较选择31个MGEX测站的30 s采样间隔观测数据进行分析,测站分布如图 3所示。

|
图 3 MGEX测站分布 Fig. 3 Distribution of MGEX stations |
为避免频间钟差等误差项对实验造成影响,采用双频无电离层静态PPP进行解算。使用GFZ发布的最终轨道产品,截止高度角设置为15°。使用开源软件GAMP进行解算,分别测试上述4种算法加密的30 s精密钟差产品及300 s钟差产品在PPP中的作用。本文设定当E、N、U方向偏差小于1 dm时滤波开始收敛,收敛后2 h的定位偏差用于统计定位精度。各测站在不同钟差产品下的PPP定位精度以及箱线图如图 4所示,表 4(单位cm)为上述31个测站PPP平均定位精度。

|
图 4 各类钟差产品不同方向PPP定位精度及箱线图 Fig. 4 PPP positioning accuracy and box plot of various clock offset products in different directions |
|
|
表 4 定位精度统计 Tab. 4 Statistics of positioning accuracy |
1) 在E、N、U方向上,滑动Lasso拟合法的平均定位精度相较于滑动最小二乘多项式拟合法、滑动拉格朗日插值法、滑动切比雪夫拟合法均有所提升。
2) 在N方向上,滑动Lasso拟合法的平均定位精度低于300 s精密钟差产品,但从各测站的定位精度可知,300 s精密钟差产品的定位精度并不总优于滑动Lasso算法,其定位精度的变化可能由多个因素的相互作用引起。
附加L1范数正则化后,Lasso算法可以有效提升最小二乘多项式拟合的定位精度,去除最小二乘多项式拟合中对拟合模型贡献较小的非必要参数的影响,修正拟合模型误差。因此,通过滑动Lasso算法插值加密的精密钟差产品可以提高PPP定位精度。
3 结语本文提出一种顾及参数稀疏的GNSS瞬时钟差模型构建算法,利用L1范数项对最小二乘多项式拟合进行约束,构建稀疏钟差模型,并使用滑动建模法对精密钟差产品进行建模。与目前常用的钟差插值加密算法进行拟合精度与PPP精度比较,得到以下结论:
1) 使用滑动Lasso拟合法建立稀疏模型能够去除最小二乘多项式拟合中对拟合模型贡献较小的非必要参数的影响,修正拟合模型误差。相比于最小二乘多项式拟合法以及目前常用的滑动拉格朗日插值法、滑动切比雪夫拟合法,滑动Lasso算法建立的瞬时钟差模型的拟合精度与PPP定位精度均有所提升。
2) 在钟差拟合建模过程中,若局部钟差数据噪声较大且跳变频繁时,使用滑动Lasso拟合法对钟差进行建模,能够更好地去除误差项过大造成的影响,修正钟差模型误差,防止钟差模型过拟合。当采用误差较大、局部跳变频繁的钟差数据进行定位时,使用滑动Lasso拟合算法进行钟差数据建模的效果优于目前常用的钟差差值拟合算法。
| [1] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1 399-1 407 (Zhang Xiaohong, Li Xingxing, Li Pan. Review of GNSS PPP and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 399-1 407)
(  0) 0) |
| [2] |
马卓希, 杨力, 贾小林, 等. 基于历元间差分模型的精密钟差加密算法研究[J]. 大地测量与地球动力学, 2016, 36(5): 415-418 (Ma Zhuoxi, Yang Li, Jia Xiaolin, et al. Research on Precise Clock Corrections Densification Based on Epoch Differential Model[J]. Journal of Geodesy and Geodynamics, 2016, 36(5): 415-418)
(  0) 0) |
| [3] |
Chen J P, Zhang Y Z, Zhou X H, et al. GNSS Clock Corrections Densification at SHAO: From 5 Min to 30 s[J]. Science China Physics Mechanics and Astronomy, 2014, 57(1): 166-175 DOI:10.1007/s11433-013-5181-7
(  0) 0) |
| [4] |
杨承午. 正则化稀疏建模方法在大地测量中的应用[D]. 徐州: 中国矿业大学, 2021 (Yang Chengwu. Regularized Sparse Modeling Method and Its Geodetic Application[D]. Xuzhou: China University of Mining and Technology, 2021)
(  0) 0) |
| [5] |
杨柳, 王钰. 泛化误差的各种交叉验证估计方法综述[J]. 计算机应用研究, 2015, 32(5): 1 287-1 290 (Yang Liu, Wang Yu. Survey for Various Cross-Validation Estimators of Generalization Error[J]. Application Research of Computers, 2015, 32(5): 1 287-1 290)
(  0) 0) |
| [6] |
Kohavi R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection[C]. International Joint Conference on Artificial Intelligence, Montreal, 1995
(  0) 0) |
| [7] |
毛亚, 王潜心, 胡超, 等. BDS-3卫星钟差特性分析[J]. 武汉大学学报: 信息科学版, 2020, 45(1): 53-61 (Mao Ya, Wang Qianxin, Hu Chao, et al. Analysis of the Characterization for BDS-3 Satellite Clock Error[J]. Geomatics and Information Science of Wuhan University, 2020, 45(1): 53-61)
(  0) 0) |
| [8] |
颜康, 常国宾, 周天, 等. 卫星钟差稀疏自回归预报模型的研究[J]. 海洋测绘, 2021, 41(4): 28-32 (Yan Kang, Chang Guobin, Zhou Tian, et al. Sparse Auto-Regressive Modeling for Satellite Clock Offsets Prediction[J]. Hydrographic Surveying and Charting, 2021, 41(4): 28-32)
(  0) 0) |
| [9] |
王润, 王井利, 吕栋. 导航卫星钟差预报的Elman神经网络算法研究[J]. 大地测量与地球动力学, 2021, 41(3): 285-289 (Wang Run, Wang Jingli, Lü Dong. Research on the Elman Neural Network Algorithm to Predict Navigation Satellite Clock Bias[J]. Journal of Geodesy and Geodynamics, 2021, 41(3): 285-289)
(  0) 0) |
| [10] |
艾孝军, 孙大伟, 贾小林, 等. GNSS星载原子钟性能评估与噪声分析模型算法研究[J]. 无线电工程, 2023, 53(5): 1 041-1 051 (Ai Xiaojun, Sun Dawei, Jia Xiaolin, et al. Research on Performance Evaluation and Noise Analysis Algorithm of GNSS On-Board Atomic Clock[J]. Radio Engineering, 2023, 53(5): 1 041-1 051)
(  0) 0) |
2. School of Spatial Information and Geomatics Engineering, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China
 2024, Vol. 44
2024, Vol. 44


