2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
3. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077;
4. 山东大学空间科学与物理学院,山东省威海市文化西路180号,264209
实时卫星钟差产品的性能直接影响全球导航卫星系统的定位、导航、授时服务质量[1]。由于星载原子钟自身的物理特性较为复杂,且极易受外界和自身因素影响,很难发现复杂的变化规律,使得建立高精度的钟差预报模型较为困难。因此,提升钟差预报的准确性是广大学者研究的重点和难点。
目前,国内外许多学者对钟差预报进行大量研究。最常用的预报模型有二次多项式(quadratic polynomial, QP)模型、灰色模型(grey model, GM)、卡尔曼滤波(Kalman filter)模型、神经网络模型,以及多种单一模型的组合预报模型和部分上述模型的改进模型[2-3]。Allan[4]提出利用二次多项式拟合预报模型对卫星钟差进行预报。崔先强等[1]将灰色模型应用于卫星钟差预报,通过与QP模型进行对比,认为GM模型相较于QP模型在长期钟差预报中具有更好的效果。郑作亚等[5]对GM模型的局限性进行改进,预报精度明显提高,模型系数随预报时间的增加逐渐趋于稳定。Davis等[6]采用Kalman滤波模型对GPS卫星钟差进行建模预报,实验表明预报1 d的精度在1 ns以内。王宇谱等[7]基于一次差分数据,利用小波神经网络(wavelet neural network, WNN)建立钟差预报模型,结果表明,差分钟差数据更适用于小波神经网络钟差预报,能明显提高短期预报精度,在此基础上提出GM和WNN组合模型。
近年来,长短时记忆(long short-term memory, LSTM)神经网络作为众多神经网络的一种,对时序数据的处理和分析具有较好的适应性,在语音识别与处理、机器翻译等多个领域被广泛应用,但在multi-GNSS卫星钟差预报中的应用研究较少,也缺少详细的对比和分析[8]。因此,本文以LSTM为基础,构建multi-GNSS卫星钟差预报模型。为验证该模型的有效性和可行性,选取QP模型、QP-LSTM模型作为对比参考,分析不同建模时长、不同预报时长情况下multi-GNSS卫星钟差LSTM模型的优势,并进一步对比分析基于LSTM模型的multi-GNSS不同卫星系统、不同原子钟类型的精度。
1 multi-GNSS卫星钟差模型构建 1.1 基于LSTM的GNSS卫星钟差预报模型 1.1.1 LSTM模型原理LSTM网络是一种时间递归神经网络(recurrent neural network, RNN),与传统的RNN不同,LSTM可以更有效地避免网络中的梯度爆炸或梯度消失问题,具有良好的应用价值[9]。LSTM单元内部结构可参考文献[10]。
1.1.2 LSTM模型构建本文采用滑动窗口法对LSTM钟差预报模型的训练样本集进行处理,输入数据为当前时刻t及其时间方向连续144或288个历元数据,以预报时刻t′+12、t′+36、t′+72、t′+144数据作为输出。滑动窗口长度为12,滑动步数为1,即原始数据确定出1个样本后,初始时刻向后推移12个历元构建下一个样本。该形式不仅可以提高数据利用率,也可以保持数据的实时更新,以提高预报精度。建模预报步骤可参考文献[10]。
1.2 二次多项式和二次多项式组合模型为验证LSTM模型的有效性,选取QP模型以及QP-LSTM模型作为比较基准。
1.2.1 二次多项式(QP)模型QP模型具有简单易操作、物理意义明确以及能够较好地反映钟差数据线性特征等优点,因此被广泛应用于钟差预测。
1.2.2 组合预报模型传统的钟差预报主要采用QP模型,其误差会随预报时间的增加而累积,因此对钟差预报具有一定局限性。本文提出一种基于QP模型和LSTM模型的GNSS卫星预报方法。利用QP模型对卫星钟差序列拟合预测结果进行提取,与LSTM模型非线性映射能力相结合,构建组合模型,该模型相较QP模型能够减小误差累积。组合模型预报流程为:首先对原始钟差进行预处理,检测并剔除粗差,得到预处理后的序列;然后利用预处理后的卫星钟差序列建立QP模型并拟合未来一段时间的钟差数据,将同时段钟差数据与拟合钟差数据的对比结果作为拟合残差序列[11];将拟合残差序列作为LSTM模型的训练样本,对二次多项式的拟合残差进行预测,得到未来时刻的预报误差,将其补偿到二次多项式的预报误差中;最后将二次多项式的钟差预报值与相对应的LSTM模型预报残差值相加得到组合模型的钟差预报值。
2 基于LSTM的GNSS卫星钟差预报模型分析与应用为比较具有不同建模弧长和预测弧长的LSTM模型、QP模型以及QP-LSTM模型的预报精度和性能,本文采用武汉大学采样间隔为300 s的快速钟差数据进行BDS-2、Galileo、GPS、GLONASS四系统建模预报,数据时间跨度为2021-06-14~20。采用12 h和24 h快速钟差序列进行建模,分别采用3种预报模型对4个系统进行1 h、3 h、6 h、12 h预报,并以对应的精密钟差作为参考,分析各系统星载原子钟的预报性能,同时对提出的LSTM模型的适用性进行验证。表 1为统一和剔除缺失数据后4个系统中各卫星的轨道类型和原子钟类型。
|
|
表 1 四系统星载原子钟的轨道类型和原子钟类型 Tab. 1 Orbit type and atomic clock type of spaceborne atomic clock of four systems |
为验证差分方法能否提升LSTM钟差预报模型的精度,分别基于原始钟差数据和一次差分数据进行LSTM钟差预报实验。以2021-06-14快速钟差进行建模,预报1 h、3 h、6 h、12 h钟差,连续预报7 d,并以精密钟差作为真值与预报结果进行对比。图 1~2为4个系统在连续预报时采用不同数据方案进行预报的精度对比,其中LSTM-1为利用预处理后的一次差分数据进行实验的结果,LSTM-2为利用预处理后的钟差序列进行实验的结果,具体对比结果见表 2(单位ns)。
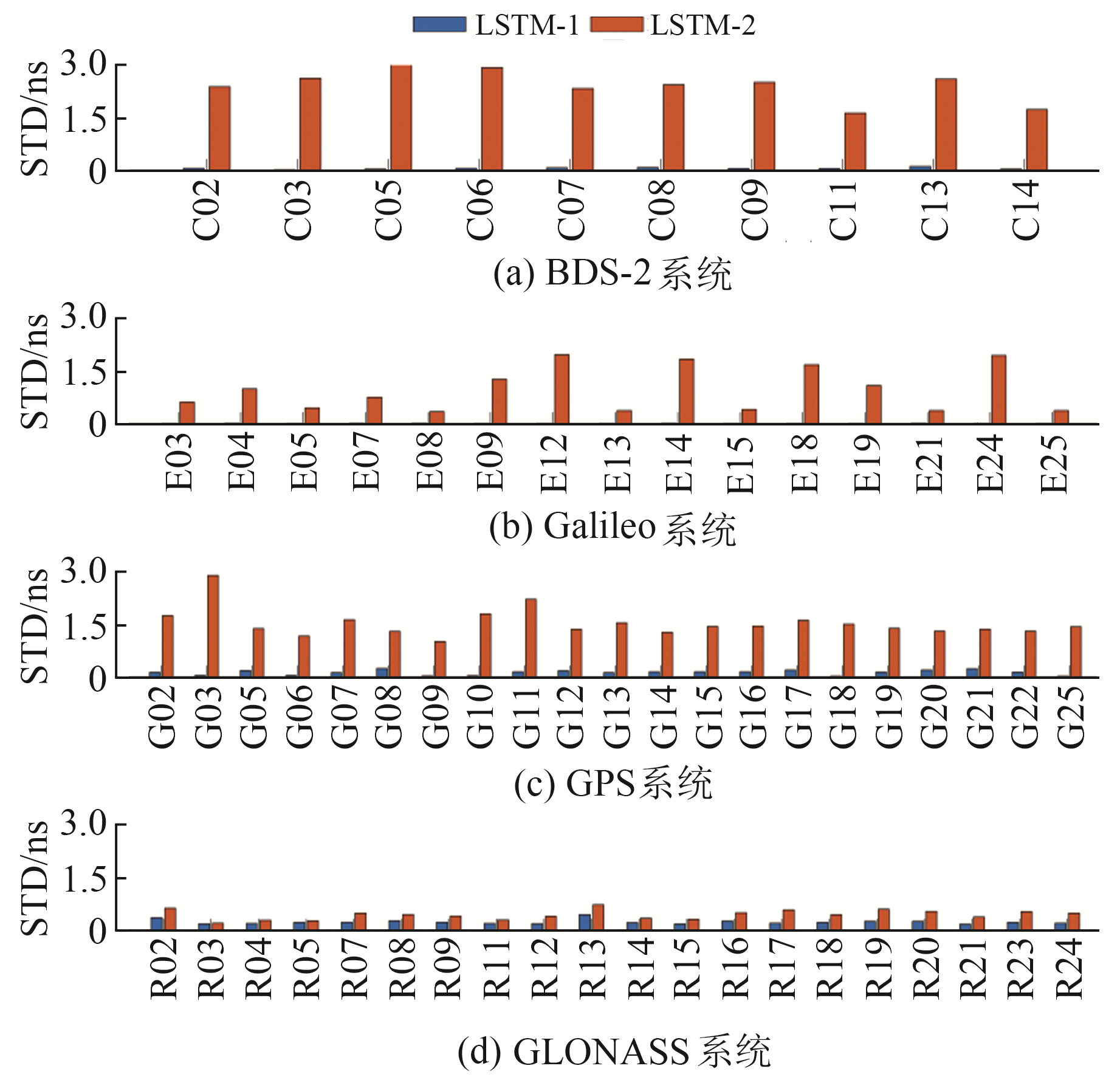
|
图 1 差分数据预报1 h结果对比 Fig. 1 Comparison of 1 h prediction result using differential data |
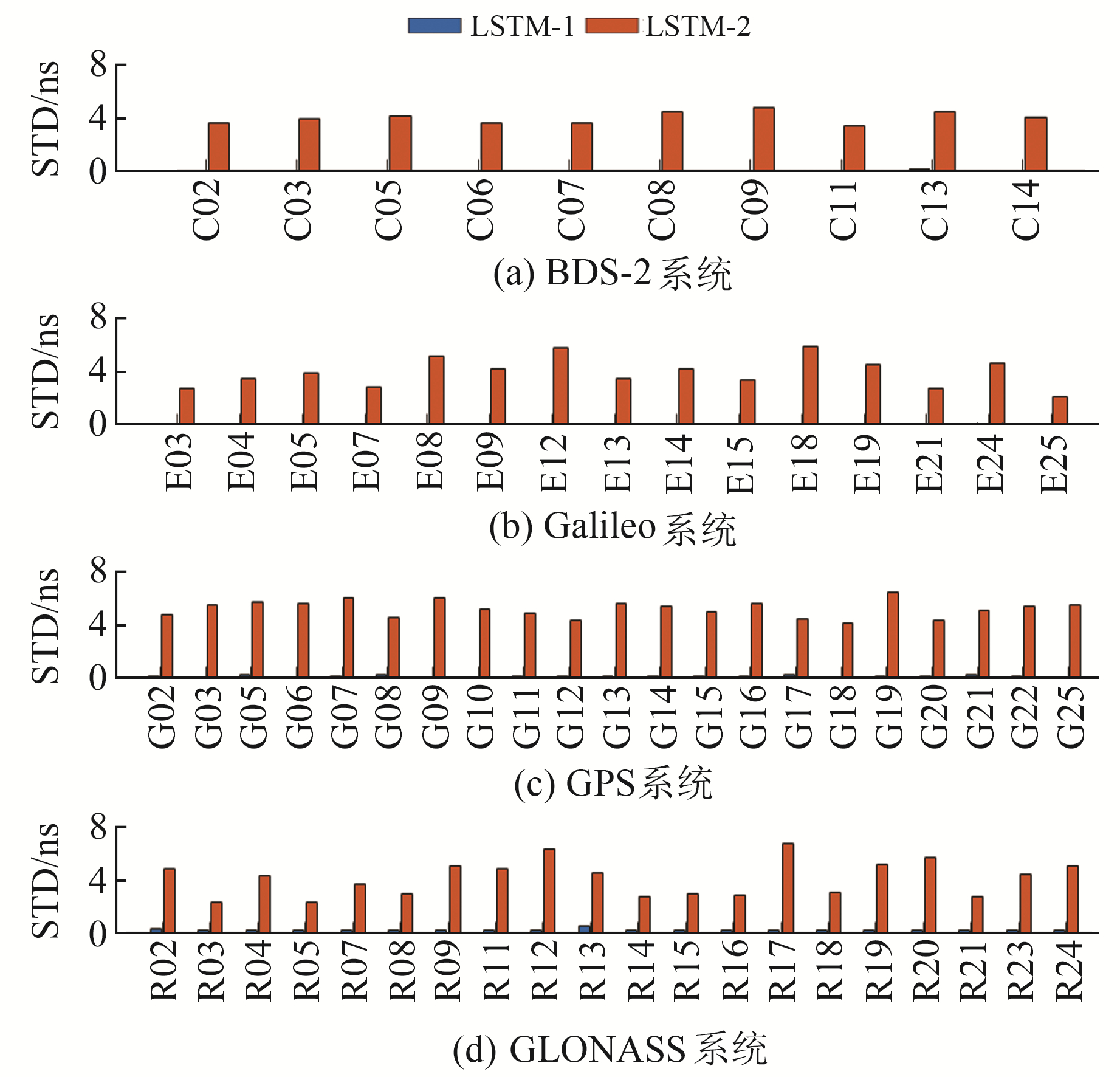
|
图 2 差分数据预报6 h结果对比 Fig. 2 Comparison of 6 h prediction result using differential data |
|
|
表 2 数据差分前后LSTM模型钟差预报精度(STD)对比 Tab. 2 Comparison of clock offset prediction accuracy of LSTM model before and after using differential data |
从图 1~2及表 2可以看出,使用原始数据进行建模时,GLONASS、GPS预报精度相对较差,次于Galileo和BDS-2。使用一次差分数据进行建模时,GLONASS预报精度最低,其精度为0.27 ns;Galileo预报精度最高,为0.02 ns;BDS-2、GPS次之,预报精度分别为0.08 ns、0.15 ns。无论短期预报还是中长期预报,在采用相同建模数据量的前提下,使用一次差分序列后的预报精度远远大于差分前精度[12],其中GLONASS、GPS提升率较高,GLONASS最大提升94%,Galileo提升率较低,同时可以看出随着预报时长增加,预报精度提升率也逐渐增加。一次差分数据变化较为平稳且数据有效位数变少,因此采用一次差分数据进行预报建模更具有合理性和优势。
2.2 不同建模时长和预报时长的LSTM模型对比基于LSTM模型对GNSS卫星钟差进行建模预报,并与QP模型、QP-LSTM模型进行对比。设置滑动窗口为1 h,即拟合以1 h为单位向前滑动,一步一预测,通过不断迭代完成目标时刻的钟差预报[13]。设计2组方案如下。
方案1:采用12 h钟差数据对各模型进行建模,预报1 h、3 h、6 h、12 h。
方案2:采用24 h钟差数据对各模型进行建模,预报1 h、3 h、6 h、12 h。
图 3~4为3种模型利用不同建模时长(12 h、24 h)预报相同时段的精度。表 3~4(单位ns)为利用相同建模时长预报不同时段(1 h、3 h、6 h、12 h)的精度统计结果。其中,poly1、zuhe1、lstm1分别为QP模型、QP-LSTM模型、LSTM模型采用方案1的预报精度,poly2、zuhe2、lstm2为QP模型、QP-LSTM模型、LSTM模型采用方案2的预报精度,高度代表模型预报精度。
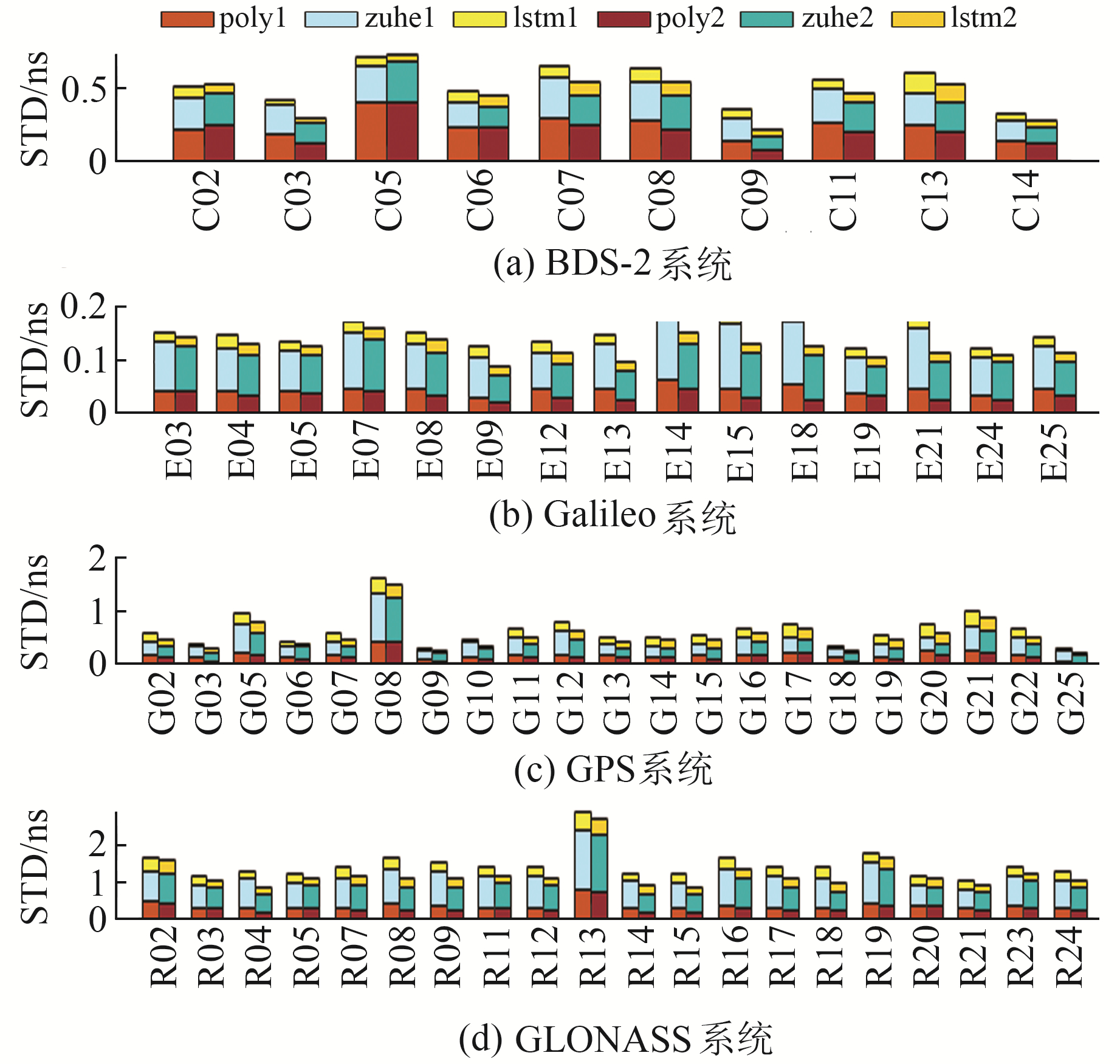
|
图 3 3种模型预报1 h钟差 Fig. 3 1 h clock offset prediction of three models |

|
图 4 3种模型预报12 h钟差 Fig. 4 12 h clock offset prediction of three models |
|
|
表 3 基于12 h钟差数据的不同系统3种模型预报1 h、3 h、6 h、12 h的平均STD统计 Tab. 3 Average STD statistics of 1 h、3 h、6 h and 12 h prediction for three models based on 12 h clock offset of different systems |
|
|
表 4 基于24 h钟差数据的不同系统3种模型预报1 h、3 h、6 h、12 h的平均STD统计 Tab. 4 Average STD statistics of 1 h、3 h、6 h and 12 h prediction for three models based on 24 h clock offset of different systems |
从图 3~4和表 3~4可以看出,对于相同的预报时段,增加钟差建模数据可以有效提升卫星钟差预报精度。对于BDS-2系统,采用12 h钟差数据建模预报1 h、3 h、6 h和12 h时,LSTM模型预报误差分别为0.073 ns、0.082 ns、0.092 ns和0.116 ns;采用24 h钟差数据建模时,LSTM模型预报误差分别为0.069 ns、0.075 ns、0.081 ns和0.098 ns,预报精度提升5%~15%。其他系统也有此规律,Galileo系统预报精度提升9%~17%,GPS系统预报精度提升5%~15%,GLONASS系统预报精度提升7%~14%。其中,Galileo系统利用24 h钟差数据建模时精度最高,精度为0.018 ns,GLONASS系统为0.242 ns,精度略低于BDS-2和GPS系统。从整体上看,采用12 h和24 h钟差数据建模时,LSTM模型精度均值均处于亚ns级,其预报精度高于QP模型和QP-LSTM模型,LSTM模型预报精度比QP-LSTM模型最高提升95%,比QP模型最高提升93%。
进一步分析不同预报时长对模型精度的影响,结果表明,利用12 h和24 h钟差数据建模预报不同时长时,从整体上看,LSTM模型预报精度较高,基本在0.018 ~0.353 ns之间,随着预报时长增加,预报精度降低5%~17%,GLONASS、GPS系统预报精度相对较差,次于Galileo和GPS系统。对于QP模型和QP-LSTM模型而言,也存在预报精度随预报时长增加而降低的现象,2种模型预报精度降低36%~56%。其中,Galileo和GPS系统预报性能较好,BDS-2系统次之,GLONASS系统预报性能最差。LSTM预报结果的稳定性明显高于其他2种模型,由于QP模型和QP-LSTM模型具有误差累积效应,随着预报时长增加,精度迅速下降。QP-LSTM模型主要受二次多项式影响,组合模型的残差可看作对QP模型的补偿与修正,QP-LSTM模型预报精度比QP模型最高提升18.2%,说明组合模型具有一定的效果。
在此基础上详细分析不同卫星钟类型模型的预报精度。对于BDS-2系统不同类型卫星而言,MEO与IGSO卫星的预报结果优于GEO卫星,Galileo系统IOV卫星钟比FOC卫星钟预报精度差。对于GPS系统,GPS Ⅲ A预报精度高于GPS Ⅱ R、GPS Ⅱ R-M、GPS Ⅱ F,多数配备Rb钟卫星的预报精度比Cs钟卫星高。对于GLONASS系统,卫星钟类型对卫星预报精度影响较小,系统内的卫星预报精度相当。PHM(Galileo)预报精度为0.018 ns,Rb(GPS Ⅱ F)、Rb(BDS-2)精度维持在0.05 ns左右;Rb(GPS Ⅲ A)、Rb(GPS Ⅱ R)、Rb(GPS Ⅱ R-M)预报精度相差不大,保持在0.15 ns左右;Cs(GPS Ⅱ F)、Cs(GLONASS)两类Cs钟预报精度在0.23 ns左右,明显差于PHM钟和Rb钟。
为验证LSTM模型的有效性,选择BDS-2、Galileo、GPS和GLONASS系统不同类型的原子钟,QP模型和组合模型同时选择不同的建模时长预报12 h作为对比,图 5为各系统卫星钟预报残差变化。

|
图 5 3种模型预报残差对比 Fig. 5 Comparison of prediction residual between the three models |
由图 5可知,QP-LSTM模型与QP模型的残差范围均在-2~14 ns之间,而LSTM模型残差为0.6 ns左右,QP-LSTM模型、QP模型随着预测时长的增加线性相关性逐渐降低,残差范围逐渐增大,发散速度比LSTM模型快[14]。使用一次差分数据的LSTM模型处理非线性数据时稳定性明显高于其他2种模型,在multi-GNSS卫星钟差预报中具有一定的可行性。E03、G05与R15的残差变化幅度相对较小,C05由于是GEO卫星钟,其残差变化幅度相对较大[15]。
3 结语本文以LSTM为基础,构建multi-GNSS卫星钟差预报模型,并与QP模型和QP-LSTM模型进行对比,验证该模型的有效性和适用性,同时分析不同卫星钟类型该模型的精度。
LSTM模型、QP模型、QP-LSTM模型的预报精度随着预报时长的增加而降低,LSTM模型在控制预报误差随时间累积方面具有明显优势,QP-LSTM模型和QP模型的预报误差会随预报时长的增加迅速变大。LSTM模型的精度受不同建模时长影响较小,具有更好的预测效果和稳定性,而QP-LSTM模型与QP模型受不同建模时长影响较大。采用LSTM模型对二次多项式拟合残差进行建模,补偿多项式模型的预报钟差,提高多项式模型精度,精度提升约4%~17%。对于multi-GNSS卫星钟差LSTM预报模型,Galileo系统稳定性最好,BDS-2和GPS次之,GLONASS稳定性最差。不同类型原子钟预报精度不同,Cs钟稳定性明显差于Rb钟和PHM钟,Block ⅡF Rb钟优于Block ⅡA Rb钟,Block ⅡR Rb钟稳定性优于Block ⅡR-M钟。在预报时长相同时,增加建模数据量可在不同程度上提升不同模型的预报精度;在建模时长相同时,不同模型的预报效果会随预报时长的增加而出现不同程度的降低。Galileo系统利用LSTM模型24小时建模数据预报1 h时,预报精度最高,预报精度为0.018 ns。综合来看,BDS-2卫星钟差采用LSTM模型较QP模型精度提升最为显著,高达68%。
| [1] |
崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报: 信息科学版, 2005, 30(5): 447-450 (Cui Xianqiang, Jiao Wenhai. Grey System Model for the Satellite Clock Error Predicting[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 447-450)
(  0) 0) |
| [2] |
廖建发, 张艳兵. 改进的多项式+周期项模型的卫星钟差预报[J]. 全球定位系统, 2018, 43(1): 91-95 (Liao Jianfa, Zhang Yanbing. Satellite Clock Error Prediction of Improved Polynomial and Periodic Model[J]. GNSS World of China, 2018, 43(1): 91-95)
(  0) 0) |
| [3] |
程佳慧, 缪新育, 赵婧妍, 等. 基于GM(1, 1)和D-MECM的钟差预报方法[J]. 北京邮电大学学报, 2022, 45(2): 44-49 (Cheng Jiahui, Miao Xinyu, Zhao Jingyan, et al. Satellite Clock Bias Prediction Based on GM(1, 1) and D-MECM[J]. Journal of Beijing University of Posts and Telecommunications, 2022, 45(2): 44-49)
(  0) 0) |
| [4] |
Allan D W. Time and Frequency(Time-Domain) Characterization, Estimation, and Prediction of Precision Clocks and Oscillators[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1987, 34(6): 647-654 DOI:10.1109/T-UFFC.1987.26997
(  0) 0) |
| [5] |
郑作亚, 陈永奇, 卢秀山. 灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J]. 天文学报, 2008, 49(3): 306-320 (Zheng Zuoya, Chen Yongqi, Lu Xiushan. An Improved Grey Model for the Prediction of Real-Time GPS Satellite Clock Bias[J]. Acta Astronomica Sinica, 2008, 49(3): 306-320)
(  0) 0) |
| [6] |
Davis J, Bhattarai S, Ziebart M. Development of a Kalman Filter Based GPS Satellite Clock Time-Offset Prediction Algorithm[C]. European Frequency and Time Forum, Gothenburg, 2012
(  0) 0) |
| [7] |
王宇谱, 吕志平, 陈正生, 等. 卫星钟差预报的小波神经网络算法研究[J]. 测绘学报, 2013, 42(3): 323-330 (Wang Yupu, Lü Zhiping, Chen Zhengsheng, et al. Research on the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 323-330)
(  0) 0) |
| [8] |
王建敏, 毕祥鑫, 黄佳鹏. BDS精密钟差短期预报[J]. 导航定位学报, 2023, 11(1): 30-38 (Wang Jianmin, Bi Xiangxin, Huang Jiapeng. Short-Term Forecast of Precision Clock Difference for BDS[J]. Journal of Navigation and Positioning, 2023, 11(1): 30-38)
(  0) 0) |
| [9] |
马冬青. 基于长短期记忆神经网络的导航卫星钟差预报[J]. 导航定位学报, 2022, 10(5): 178-184 (Ma Dongqing. Study on Navigation Satellite Clock Error Prediction Based on LSTM[J]. Journal of Navigation and Positioning, 2022, 10(5): 178-184)
(  0) 0) |
| [10] |
王锐, 弓剑军, 杜洪强, 等. 基于长短时记忆神经网络(LSTM)的钟差预报算法[J]. 宇航计测技术, 2022, 42(5): 57-62 (Wang Rui, Gong Jianjun, Du Hongqiang, et al. Long Short Term Memory Neural Network(LSTM) Based on Clock Difference Forecasting Algorithm[J]. Journal of Astronautic Metrology and Measurement, 2022, 42(5): 57-62)
(  0) 0) |
| [11] |
赵丹宁, 雷雨. GLONASS星载原子钟的长期特性分析[J]. 武汉大学学报: 信息科学版, 2021, 46(6): 895-904 (Zhao Danning, Lei Yu. Long-Term Characteristics Analysis of GLONASS In-Flight Clocks[J]. Geomatics and Information Science of Wuhan University, 2021, 46(6): 895-904)
(  0) 0) |
| [12] |
陈晓阳. LSTM卫星钟差预报模型建立与预报方法研究[D]. 青岛: 山东科技大学, 2020 (Chen Xiaoyang. Research on Modeling and Forecast Method of the LSTM Satellite Clock Bias Forecast Model[D]. Qingdao: Shandong University of Science and Technology, 2020)
(  0) 0) |
| [13] |
Ge H B, Li B F, Wu T H, et al. Prediction Models of GNSS Satellite Clock Errors: Evaluation and Application in PPP[J]. Advances in Space Research, 2021, 68(6): 2 470-2 487
(  0) 0) |
| [14] |
Huang B H, Ji Z X, Zhai R J, et al. Clock Bias Prediction Algorithm for Navigation Satellites Based on a Supervised Learning Long Short-Term Memory Neural Network[J]. GPS Solutions, 2021, 25(2)
(  0) 0) |
| [15] |
陈亮. 北斗/GNSS实时精密卫星轨道钟差产品组合理论与方法研究[D]. 武汉: 武汉大学, 2021 (Chen Liang. Research on the Theory and Method of BDS/GNSS Real-Time Precise Satellite Orbit and Clock Products Combination[D]. Wuhan: Wuhan University, 2021)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Sate Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China;
4. School of Space Science and Physics, Shandong University, 180 West-Wenhua Road, Weihai 264209, China
 2024, Vol. 44
2024, Vol. 44

