2. 中国科学院大学,北京市玉泉路19号甲,100049;
3. 中国科学院时间频率基准重点实验室,西安市书院东路3号,710600
高精度远程时间传递技术是实现两地时钟比对、测试评估守时系统性能的重要手段。常用的高精度远程时间传递技术主要有卫星双向时间频率传递(two way satellite time and frequency transfer, TWSTFT)、全球导航卫星系统(global navigate satellite system, GNSS)时间频率传递、光纤时间频率传递等[1-3]。TWSTFT和光纤时间频率传递的频率稳定度较GNSS时间频率传递法更优,但设备及实施费用昂贵;GNSS时间频率传递具有设备简单、操作方便、成本低等优点。
GNSS时间频率传递是远程时频传递的关键技术之一[4-5]。根据采用GNSS观测值和观测模型的不同,GNSS时间频率传递可分为GNSS CV、AV、载波相位时间传递(carrier phase time transfer,CP TT)法。其中GNSS CP TT由于采用载波相位作为基本观测量,测量精度比码伪距高2~3个数量级,时间传递准确度和频率传递短期稳定度均更优[6-7],并且从20世纪90年代开始就成为GNSS时间频率传递的研究热点,其典型代表GPS PPP自2009年就被国际权度局(BIPM)用于国际原子时(TAI)和协调世界时(UTC)的计算[8]。
守时系统是时频信号产生的基础,尤其是氢钟、铯钟等组成的高精度守时系统对国民经济和国防建设至关重要。高精度守时系统组成复杂,很难用常规手段对其性能进行测试评估,这会给守时系统定期检测与校准造成很大困难。为解决该问题,国内外学者相继提出基于GNSS CV和AV的远程测试方法[9]。研究表明,基于GPS CV和AV可实现时间测量优于5 ns、频率测量优于6×10-14/d[10]。GNSS载波相位共视(PCV)和PPP时间测量均优于百ps量级,频率稳定度优于10-15/d。因此,近两年来国家时间频率体系建设中频率稳定度设计指标为10-15/d量级的守时系统测试评估工作,可采用GNSS PCV和PPP时间传递法来展开。
为测试评估国家时间频率体系所建守时系统的性能,采用PCV和PPP远程测试方法评估待测守时系统的相对频率偏差、频率稳定度等特性。结果表明,PPP和PCV法可准确测量并反映守时系统的真实性能,可为下一步在建守时系统的测试验收打下坚实基础。
1 GNSS CP TT数学模型基于码伪距和载波相位测量的GNSS基本观测模型可参考文献[11]。
1.1 PPP时间传递数学模型传统PPP通常采用双频无电离层码伪距和载波相位组合模型,表达式为:
| $ \begin{gathered} P_{\mathrm{IF}}=\frac{f_1^2 P_1-f_2^2 P_2}{f_1^2-f_2^2}=r+c\left(T_{\mathrm{u}}-T^{\mathrm{s}}\right)+ \\ d_{\mathrm{trop}}+d_{P_{\mathrm{IF}}}+d_{\mathrm{mul} / P_{\mathrm{IF}}}+\varepsilon_{P_{\mathrm{IF}}} \end{gathered} $ | (1) |
| $ \begin{gathered} L_{\mathrm{IF}}=\frac{f_1^2 L_1-f_2^2 L_2}{f_1^2-f_2^2}=r+c\left(T_{\mathrm{u}}-T^{\mathrm{s}}\right)+ \\ d_{\text {trop }}+d_{L_{\mathrm{IF}}}+\lambda_{\mathrm{IF}} N_{\mathrm{IF}}+d_{\mathrm{mul} / L_{\mathrm{IF}}}+\varepsilon_{L_{\mathrm{IF}}} \end{gathered} $ | (2) |
式中,PIF和LIF分别表示无电离层码伪距和载波相位组合观测值,单位m;f1和f2为2种载波的频率,单位Hz;P1、P2和L1、L2分别为2个频率的伪距观测值和载波观测值,单位m;r为星站间几何距离,单位m;Ts和Tu分别为卫星s和接收机u的钟差,即卫星钟、接收机钟与参考时间基准之差,单位s;dtrop为对流层时延,单位m;λIF为波长,单位m/周;NIF为组合模糊度,单位周;dPIF和dLIF分别为伪码和载波相位在接收机内的时延,单位m;dmul/PIF和dmul/LIF分别为伪码和相位观测值中的多路径误差,单位m;εPIF、εLIF分别为伪码和载波相位测量噪声与其他未模型化的误差,单位m。
1.2 PCV时间传递数学模型PCV是一种站间单差载波相位模型,在两测站分别获得无电离层组合码伪距和载波相位观测值后进行站间单差,然后直接解算获得两地相对钟差。观测模型可表示为:
| $ \begin{gathered} \Delta P_{\mathrm{IF}}=\Delta r+c \Delta T_{\mathrm{u}}+\Delta d_{\text {trop }}+ \\ \Delta d_{P_{\mathrm{IF}}}+\Delta d_{\mathrm{mul} / P_{\mathrm{IF}}}+\Delta \varepsilon_{P_{\mathrm{IF}}} \end{gathered} $ | (3) |
| $ \begin{gathered} \Delta L_{\mathrm{IF}}=\Delta r+c \Delta T_{\mathrm{u}}+\Delta d_{\text {trop }}+\Delta d_{L_{\mathrm{IF}}}+ \\ \lambda_{\mathrm{IF}} \Delta N_{\mathrm{IF}}+\Delta d_{\mathrm{mul} / L_{\mathrm{IF}}}+\Delta \varepsilon_{L_{\mathrm{IF}}} \end{gathered} $ | (4) |
式中,Δ表示两测站某参量之差,其他参量含义与上文中PPP时间传递数学模型一致。与PPP不同的是,PCV法可很好地消除卫星轨道和钟差等误差,直接解算获得两地时差。
1.3 基于GNSS CP TT的守时系统远程性能评估原理基于GNSS CP TT的守时系统远程性能测试评估原理和装置连接图如图 1所示。
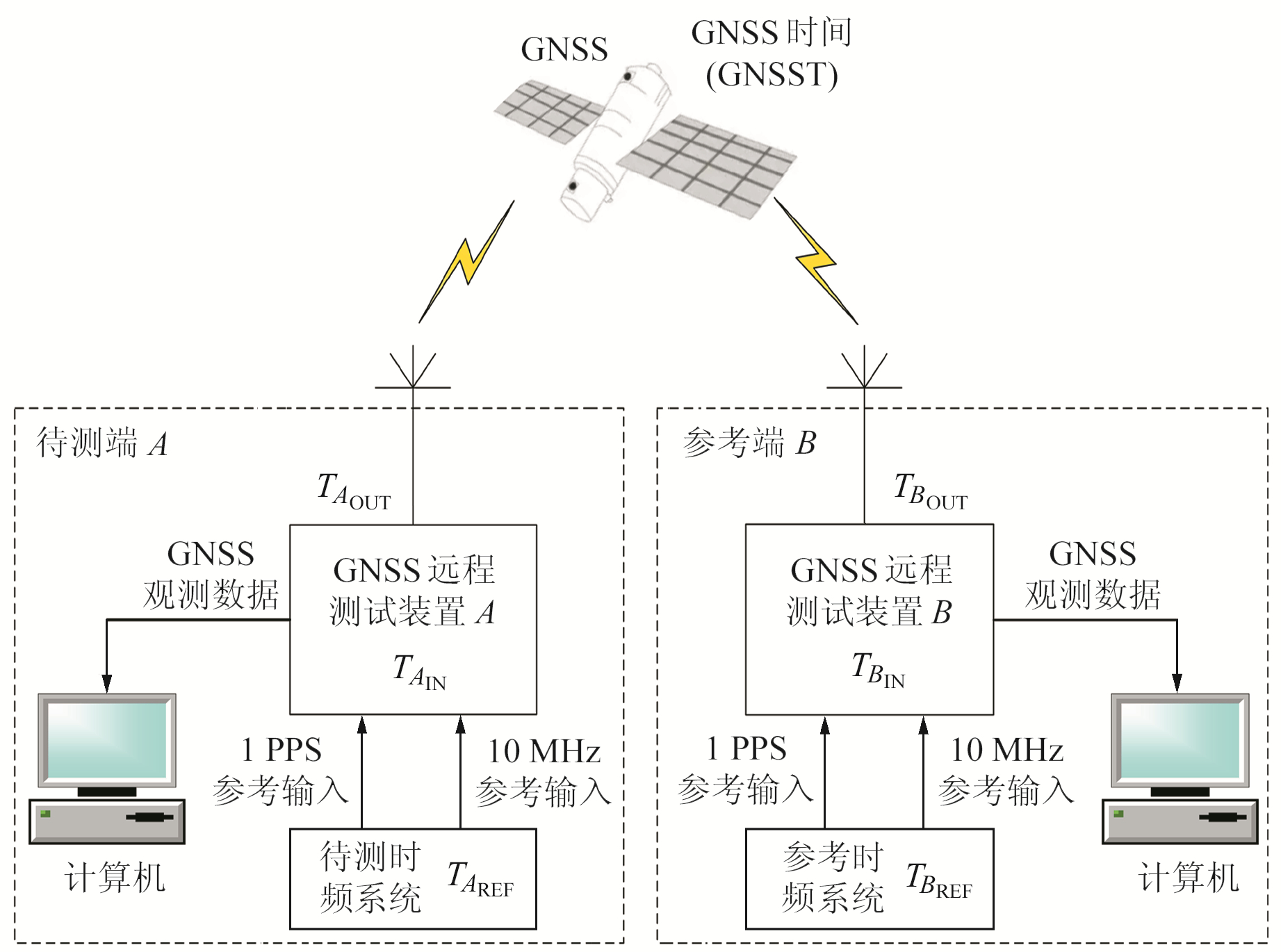
|
图 1 基于GNSS CP TT的守时系统远程性能评估装置连接图 Fig. 1 Connection diagram of time keeping system performance evaluation device based on GNSS CP TT |
利用GNSS接收机获取待测端和参考端的GNSS观测数据,通过解算分别得到TAOUT和TBOUT与参考时间REFT之差ΔTA和ΔTB,表达式为:
| $ \Delta T_{A / B}=T_{A_{\text {OUT }} / B_{\text {OUT }}}-\text { REFT } $ | (5) |
通常利用IGS/MGEX分析中心的精密星历和精密钟差,以IGST或某测站外界时钟REFCLK为参考,得到卫星钟差。因此,接收机钟差也可以IGST/REFCLK为参考,A、B两地时间频率标准比对结果ΔTAB可表示为:
| $ \begin{gathered} \Delta T_{A B}=\left(T_{A_{\mathrm{OUT}}}-\mathrm{IGST} / \mathrm{REFCLK}\right)- \\ \left(T_{B_{\mathrm{OUT}}}-\mathrm{IGST} / \mathrm{REFCLK}\right)=\Delta T_A-\Delta T_B \end{gathered} $ | (6) |
为验证GNSS PPP和PCV方法用于远程守时系统性能测试的效果,选取位于西安临潼的中国科学院国家授时中心(national time service center, NTSC)保持的国家标准时间UTC(NTSC)为参考。在西安和北京两地通过GNSS远程测试与验证装置分别获取4个测站2023-03-30~04-13(MJD:60 033~60 047)共15 d的GNSS观测数据,将XIA6测站作为参考测站,分别与其他3个测站构成零基线(XIA6-SE22)、短基线(XIA6-NU17)和长基线(XIA6-GT01)三种时间传递链路。实验所选测站信息见表 1。
|
|
表 1 所选测站信息 Tab. 1 Information of the selected stations |
实验采用PPP、PCV两种时间传递方法分别对两地时差进行解算,得到各地时间与UTC(NTSC)的偏差。PPP和PCV数据处理流程如图 2和图 3所示。

|
图 2 PPP时间传递数据处理流程 Fig. 2 Data processing flow chart of PPP time transfer |
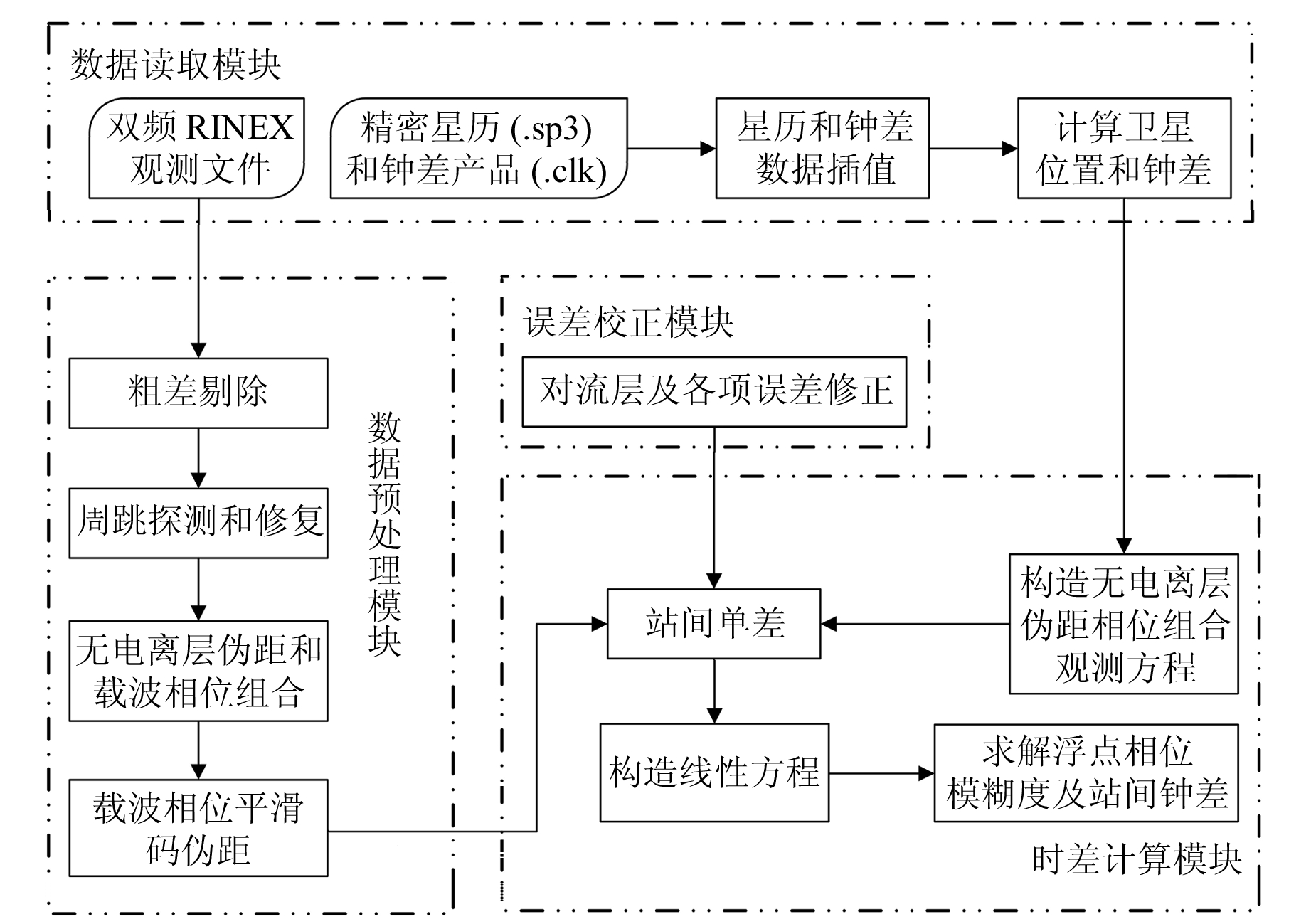
|
图 3 PCV时间传递数据处理流程 Fig. 3 Data processing flow chart of PCV time transfer |
实验中PCV和PPP时间传递均采用静态模式解算,参数估计策略详见表 2。
|
|
表 2 PPP/PCV参数估计策略 Tab. 2 Parameters estimation strategies of PPP/PCV |
守时系统一般以频率稳定度和相对频率偏差来表征其性能,在获得待测守时系统相对参考守时系统时差后,为区分调相闪烁噪声和调相白噪声,通常采用修正阿伦偏差(modified Allan deviation, MDEV)表征频率稳定度。
评估待测守时系统性能的参考守时系统的相对频率偏差至少比待测守时系统高1个量级,频率稳定度至少比待测守时系统高3倍。国家标准时间UTC(NTSC)频率准确度为5×10-15,短期频率稳定度可达到10-16/d量级,完全满足对时间频率参考的要求。
3.2 零基线实验选取临潼园区2个测站构成零基线链路XIA6-SE22,两测站接收机及天线同型号,均外接UTC(NTSC)。图 4为XIA6-SE22链路的PCV和PPP时间传递结果,PCV时间传递结果的标准偏差(STD)为0.03 ns,PPP时间传递结果的STD为0.09 ns。相比PPP时间传递结果,PCV结果波动幅度小,说明PCV时间传递链路的噪声水平更小,时间传递准确度更高。由图 5可知,PCV和PPP时间传递结果的频率稳定度分别为2×10-16/d和5×10-16/d,且在平均时间小于1 d时,零基线链路PCV结果的频率稳定度同样优于PPP时间传递结果。

|
图 4 XIA6-SE22链路的PCV和PPP时间传递结果 Fig. 4 PCV and PPP time transfer results of XIA6-SE22 time link |

|
图 5 XIA6-SE22链路PCV和PPP时间传递结果的频率稳定度 Fig. 5 Frequency stability of PCV and PPP time transfer results of XIA6-SE22 time link |
从同源零基线PCV和PPP时间传递结果可以看出,PCV链路的噪声很小,而PPP链路的噪声更大。
3.3 短基线实验选取西安临潼园区XIA6测站和航天城NU17测站构成短基线链路XIA6-NU17,NU17测站位于国家授时中心西安航天城园区,与临潼园区相距33 km。NU17测站接收机外接时间频率参考为1台国产氢原子钟。
图 6为XIA6-NU17链路的PCV和PPP时间传递结果,PCV时间传递结果的STD为0.59 ns,PPP时间传递结果的STD为0.89 ns,可以看出PCV时间传递链路的噪声相对稍小。
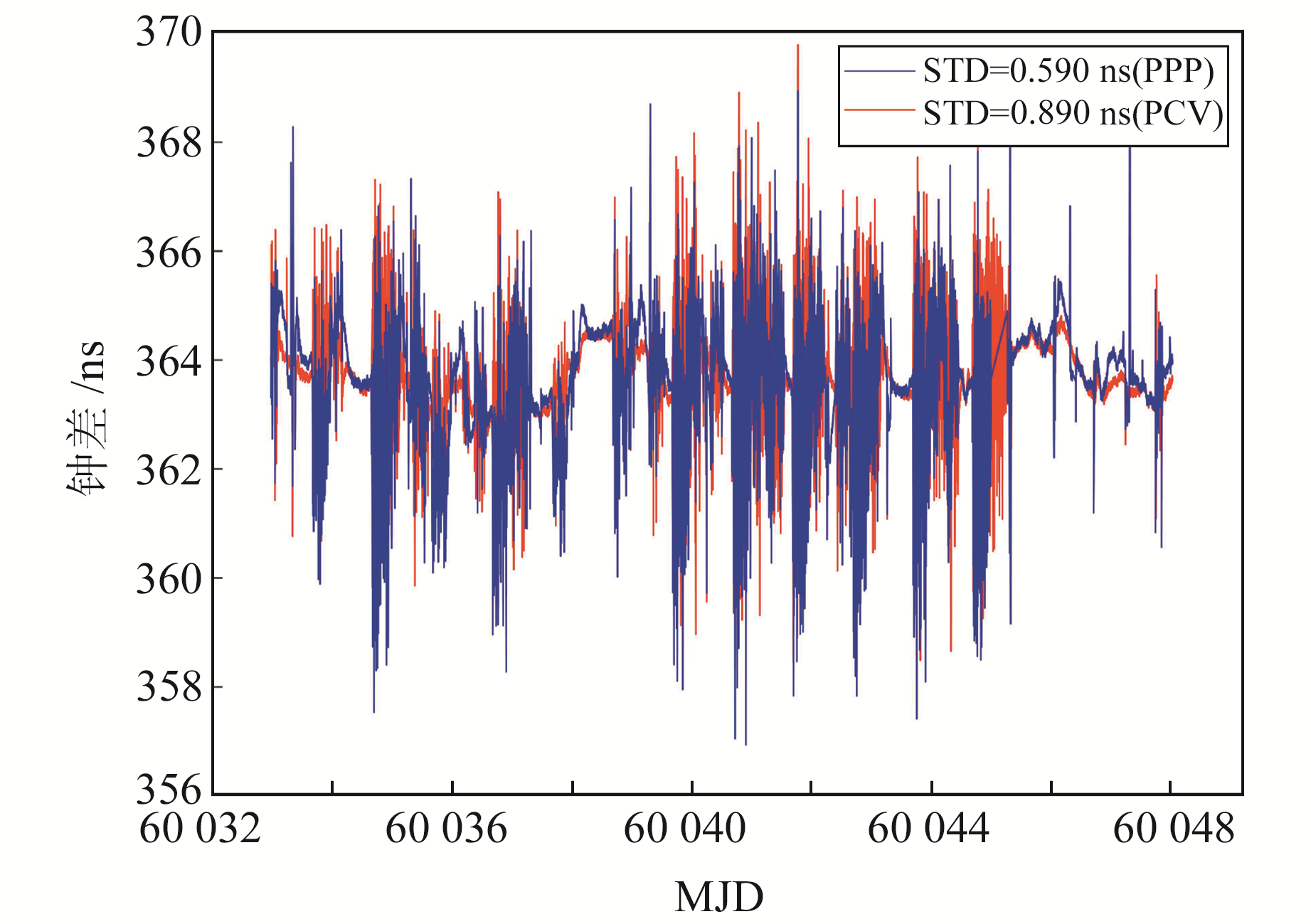
|
图 6 XIA6-NU17链路的PCV和PPP时间传递结果 Fig. 6 PCV and PPP time transfer results of XIA6-NU17 time link |
图 7为PCV和PPP时间传递结果的频率稳定度,可以看出,PCV和PPP时间传递结果的频率稳定度均约为4×10-15/d,而该国产氢钟的频率稳定度为10-14/d量级,说明采用PCV和PPP时间传递可准确反映NU17测站接收机外接氢原子钟的频率稳定度特性。同时,短基线链路平均时间小于1 000 s时,PCV时间传递的频率稳定度与PPP时间传递的频率稳定度相当,而当平均时间在1 000 s与1 d之间时,PPP时间传递结果的频率稳定度相对较差,这主要是由PPP时间链路的噪声引起。
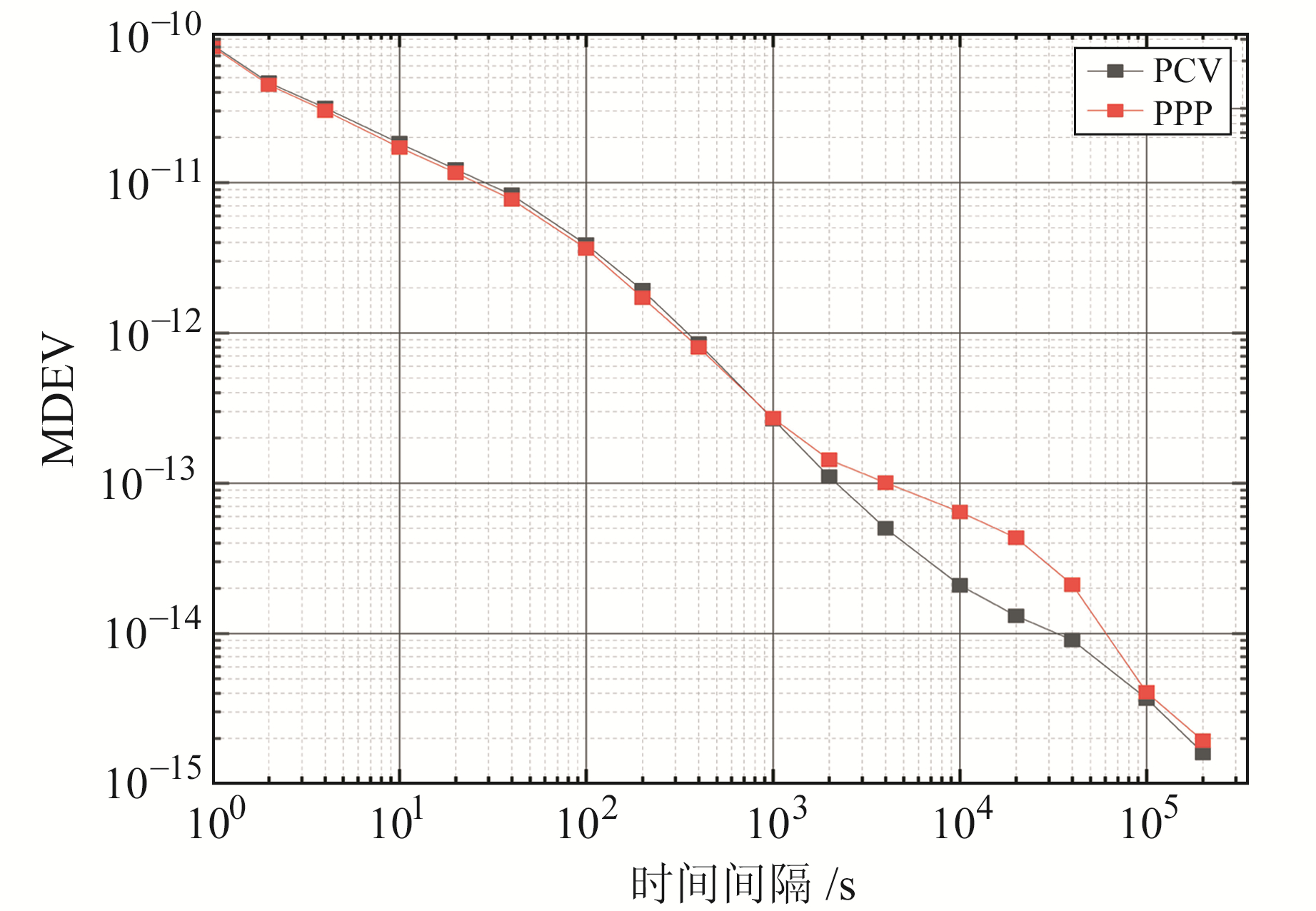
|
图 7 XIA6-NU17链路PCV和PPP时间传递结果的频率稳定度 Fig. 7 Frequency stability of PCV and PPP time transfer results of XIA6-NU17 time link |
图 8为采用PCV和PPP解算的NU17-XIA6链路的相对频率偏差,从图中可以看出,PCV和PPP时间传递的平均相对频率偏差分别为6.55×10-15和7.24×10-15,而该国产氢钟的相对频率偏差约为5×10-14,这也说明PCV和PPP时间传递结果可准确反映待测氢原子钟的相对频率偏差特性。

|
图 8 XIA6-NU17链路PCV和PPP时间传递结果的相对频率偏差 Fig. 8 Relative frequency deviation of PCV and PPP time transfer results of XIA6-NU17 time link |
选取临潼园区XIA6测站和北京GT01测站构成长基线链路XIA6-GT01,GT01测站位于北京,与临潼园区相距1 100 km。GT01测站接收机外接时间频率参考为国家时间频率体系新建守时系统,采用氢-铯联合守时,钟组规模大,设计指标中频率稳定度为3×10-15/d、频率准确度为10-14。
图 9为XIA6-GT01链路的PCV和PPP时间传递结果,PCV时间传递结果的STD为1.15 ns,PPP时间传递结果的STD为1.08 ns。由图可知,PPP和PCV时间传递曲线在天与天交界处存在规律性跳变,并且PCV时间传递的跳变值小于PPP时间传递的跳变值,这主要是由于PCV和PPP时间传递通常以1 d为1个批单元,码噪声和卫星精密产品相邻天之间的时间基准不一致等原因所致。PCV时间传递无需卫星精密钟差产品,因此采用PCV时间传递比采用PPP时间传递引起的日界不连续误差更小[11]。另外也可以看出,作为该守时系统主钟的氢原子钟组存在频率漂移现象。

|
图 9 XIA6-GT01链路的PCV和PPP时间传递结果 Fig. 9 PCV and PPP time transfer results of XIA6-GT01 time link |
图 10为PCV和PPP时间传递的频率稳定度,可以看出,PCV和PPP时间传递结果的频率稳定度均约为3.2×10-15/d,基本可反映该守时系统的频率稳定度特性。随着平均时间增加,PPP链路的频率稳定度越来越接近PCV链路,说明增加观测时长,采用PCV和PPP均可准确反映该高精度守时系统的频率稳定度特性。

|
图 10 XIA6-GT01链路PCV和PPP时间传递结果的频率稳定度 Fig. 10 Frequency stability of PCV and PPP time transfer results of XIA6-GT01 time link |
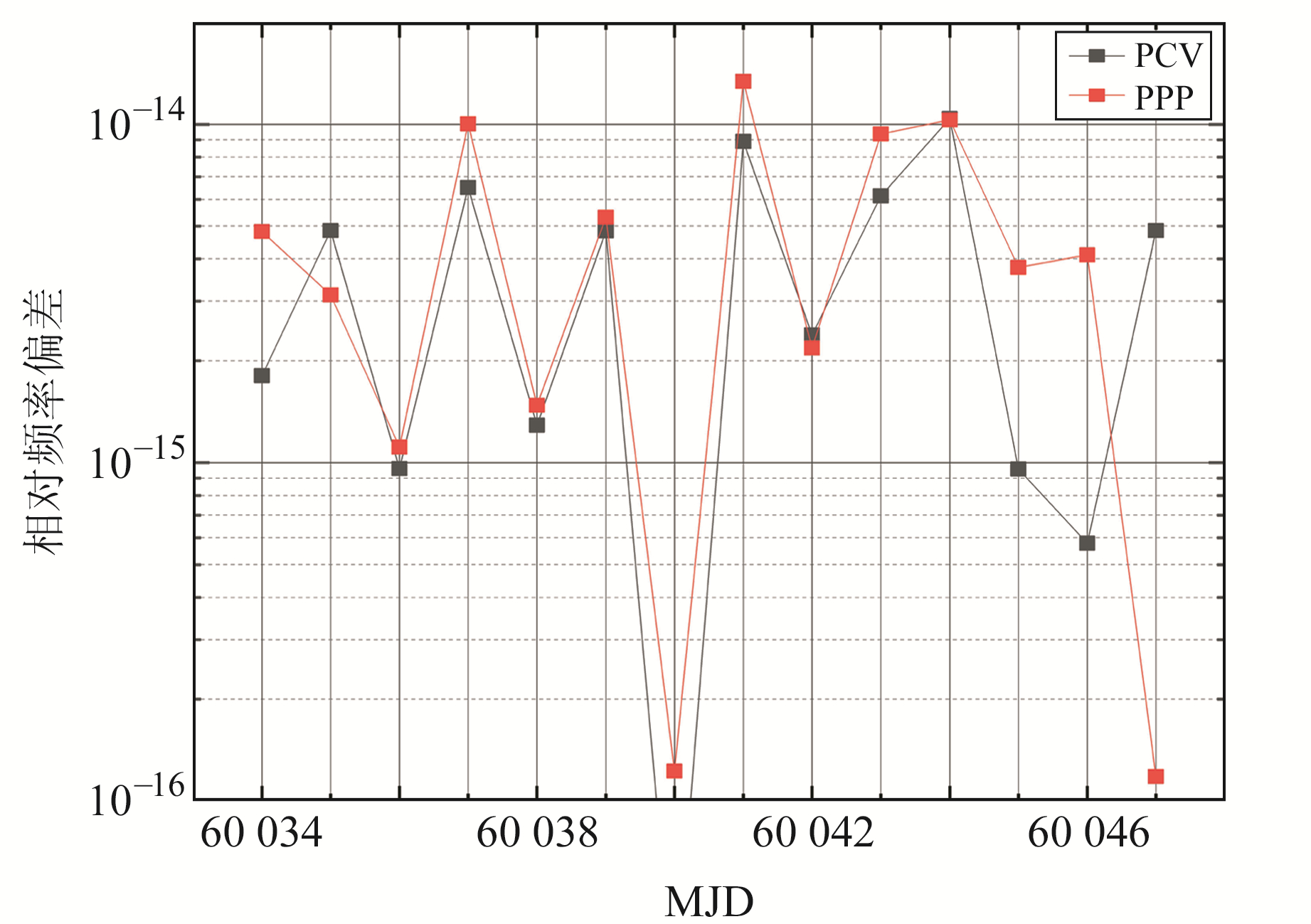
图 11为采用PCV和PPP解算的待测守时系统的相对频率偏差,PCV链路的平均相对频率偏差为3.89×10-15,PPP链路的平均相对频率偏差为4.95×10-15,也可反映该守时系统的相对频率偏差特性。
|
图 11 XIA6-GT01链路PCV和PPP时间传递结果的相对频率偏差 Fig. 11 Relative frequency deviation of PCV and PPP time transfer results of XIA6-GT01 time link |
由以上实验结果可以看出,随着基线长度增加,PCV和PPP时间传递的STD差值越来越小,在长基线情况下,PPP时间传递的STD小于PCV时间传递。这是由于随着基线长度增加,PCV可用卫星数量越来越少,PCV和PPP时间传递能力越来越相近,甚至在更长基线时,PPP时间传递的能力优于PCV时间传递。
4 结语为测试评估在建守时系统的频率稳定度、相对频率偏差等性能,提出基于GNSS PCV和PPP的远程测试评估方法,以国家标准时间UTC(NTSC)为参考,选取位于西安和北京的4个不同测站组成不同基线时间链路,分别开展15 d的验证实验,得到以下结论:
1) 相比PPP时间传递,PCV时间传递链路噪声更小,时间传递准确度更高,长期频率稳定度更优。
2) 基于PCV和PPP时间传递的远程测试方法可用于频率稳定度为10-15/d、相对频率偏差为10-14的高精度守时系统性能评估,可准确反映高精度守时系统的频率稳定度和相对频率偏差特性。
致谢: 感谢国家空间科学数据中心(http://www.nssdc.ac.cn)、iGMAS国家授时中心分析中心提供测试软件。
| [1] |
郭海荣, 杨生, 杨元喜, 等. 基于卫星双向时间频率传递进行钟差预报的方法研究[J]. 武汉大学学报: 信息科学版, 2007, 32(1): 43-46 (Guo Hairong, Yang Sheng, Yang Yuanxi, et al. Numerical Prediction Methods for Clock Difference Based on Two-Way Satellite Time and Frequency Transfer Data[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 43-46)
(  0) 0) |
| [2] |
陈法喜, 赵侃, 李博, 等. 基于1 085 km实地光纤链路的双波长光纤时间同步研究[J]. 物理学报, 2021, 70(7) (Chen Faxi, Zhao Kan, Li Bo, et al. High-Precision Dual-Wavelength Time Transfer via 1 085 km Telecommunication Fiber Link[J]. Acta Physica Sinica, 2021, 70(7))
(  0) 0) |
| [3] |
Delporte J, Mercier F. Progress in Accurate Frequency Transfer by GPS and GEO Carrier Phase at CNES[C]. IEEE International Frequency Control Symposium and PDA Exhibition Jointly with the 17th European Frequency and Time Forum, Tampa, 2003
(  0) 0) |
| [4] |
李永萍, 屈俐俐. NTSC-PTB链路的GPS全视法时间比对数据分析[J]. 时间频率学报, 2012, 35(3): 143-147 (Li Yongping, Qu Lili. Analysis of GPS AV Time Comparison between NTSC and PTB[J]. Journal of Time and Frequency, 2012, 35(3): 143-147)
(  0) 0) |
| [5] |
张小红, 蔡诗响, 李星星, 等. 利用GPS精密单点定位进行时间传递精度分析[J]. 武汉大学学报: 信息科学版, 2010, 35(3): 274-278 (Zhang Xiaohong, Cai Shixiang, Li Xingxing, et al. Accuracy Analysis of Time and Frequency Transfer Based on Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 274-278)
(  0) 0) |
| [6] |
Defraigne P, Baire Q, Guyennon N. GLONASS and GPS PPP for Time and Frequency Transfer[C]. IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum, Geneva, 2007
(  0) 0) |
| [7] |
高喆, 张继海, 王翔, 等. 北斗亚欧全视时间比对试验[J]. 天文学报, 2020, 61(1): 35-43 (Gao Zhe, Zhang Jihai, Wang Xiang, et al. Experiment of Beidou Asia-Euro All-in-View Time Transfer[J]. Acta Astronomica Sinica, 2020, 61(1): 35-43)
(  0) 0) |
| [8] |
Petit G, Jiang Z. Precise Point Positioning for TAI Computation[C]. IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum, Geneva, 2007
(  0) 0) |
| [9] |
Kong Y, Yang X H, Chang H, et al. Method of Precise Common-View Frequency Transfer Based on Beidou GEO Satellite[C]. IEEE International Frequency Control Symposium(FCS), Taipei, 2014
(  0) 0) |
| [10] |
郭栋, 董绍武, 武文俊, 等. 北斗三号多频点双频组合共视时间传递性能分析[J]. 天文学报, 2020, 61(6): 78-89 (Guo Dong, Dong Shaowu, Wu Wenjun, et al. Analysis on Dual-Frequency Combination Common View Time Transfer Performance Based on Beidou-3 Multi-Frequencies[J]. Acta Astronomica Sinica, 2020, 61(6): 78-89)
(  0) 0) |
| [11] |
张向波, 郭际, 胡永辉, 等. 日界不连续误差对GNSS载波相位频率传递的影响[J]. 大地测量与地球动力学, 2022, 42(4): 371-377 (Zhang Xiangbo, Guo Ji, Hu Yonghui, et al. Influence of Day-Boundary Discontinuities on GNSS Carrier Phase Frequency Transfer[J]. Journal of Geodesy and Geodynamics, 2022, 42(4): 371-377)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
3. Key Laboratory of Time and Frequency Primary Standards, CAS, 3 East-Shuyuan Road, Xi'an 710600, China
 2024, Vol. 44
2024, Vol. 44

