2. 中国地质环境监测院,北京市大慧寺20号,100081;
3. 自然资源部地质灾害智能监测与风险预警工程技术创新中心,北京市大慧寺20号,100081;
4. 武汉大学测绘学院,武汉市珞喻路129号,430079;
5. 中国地质大学(北京)信息工程学院,北京市学院路29号,100083;
6. 中国地质大学(武汉)地理与信息工程学院,武汉市鲁磨路388号,430074
全球导航卫星系统(global navigation satellite system, GNSS)具有连续高精度、全天候监测、可直接提供三维变形信息等优势,已广泛应用于桥梁、水库大坝、尾矿库以及滑坡、沉降等地质灾害的变形监测[1-2]。然而,受数据采集和通讯、观测值粗差、多路径效应等GNSS观测值质量因素以及GNSS定位软件性能的影响,GNSS精密定位获取的三维位移监测序列中不可避免地存在粗差。因此,识别并剔除GNSS监测位移数据中的异常值,对提升GNSS监测的准确性,降低自动化监测预警的误报、漏报概率具有重要意义。
异常检测是数据挖掘的基础问题之一,常用的方法有基于数理统计、聚类分析、数据挖掘、机器学习的方法等。针对GNSS变形监测时间序列中的粗差处理问题,吴浩等[3]提出一种基于小波分析的改进型3σ(本文简称小波-3σ)粗差探测方法,对GNSS位移序列中3σ~5σ粗差的探测效果较好,但难以剔除序列中的较小粗差;文献[4-5]分别采用奇异谱分析、小波分析方法识别变形监测序列中的粗差。聚类方法中最常用的算法为K-means算法,其是利用异常值离群的特性,但聚类结果易受初始随机聚类中心和样本离群点的影响[6]。Hochreiter等[7]提出长短期记忆网络算法(long short-term memory, LSTM),因其在处理单变量时序数据方面的优势,近年来诸多学者提出基于LSTM的异常检测算法。然而,上述大多数异常检测算法为事后处理模式,难以满足GNSS位移序列粗差的实时性、可靠性检测需求。因此,需要一种初始化简易、能实时适应数据变化、时间复杂度小的GNSS位移监测数据异常值实时检测算法。
稳健随机分割森林(RRCF)算法是一种面向动态数据流的异常值检测算法[8]。该算法在数据流上动态维护随机分割树的分布,并根据新样本点的插入或删除对分割树复杂度的影响来评判其异常程度。RRCF算法能通过一次遍历样本集获得每个样本点的异常评分,具有较好的运行效率,已在城市交通、水质监测、互联网性能指标分析等领域得到广泛应用并取得较好的效果[9-11]。
本文旨在研究基于RRCF的GNSS监测位移数据异常实时检测方法。首先介绍RRCF算法的原理,然后介绍基于RRCF的GNSS监测位移数据异常实时检测算法流程,最后通过仿真和实测数据评估算法性能。
1 RRCF算法RRCF算法的基本原理是在数据流上动态维护二叉树,即稳健随机分割树(robust random cut tree, RRCT)结构的分布。给定样本集S生成的树T(S),样本集中每个元素对应树T(S)中的叶子节点,非叶子节点为其左右子节点的集合,根节点对应样本集S,S上的RRCT生成如下[8]:
1) 假设样本数据为{x1, …, xi};
2) 选取Xi,其中Xi符合[minx∈Sxi, maxx∈Sxi] 上的均匀分布;
3) 将S分割为左右子树S1={x|x∈S, x≤Xi}、S2=S-S1,并对S1、S2进行递归分割,直到所有样本点均在叶子节点上。
RRCF就是一组相互独立的稳健随机分割树(RRCT),其核心问题是异常定义以及RRCF在数据流上的动态维护[8]。
1.1 RRCF动态维护给定样本集S构建的树Tree1,将x点从Tree1中插入或删除得到的树Tree2与直接由样本集S±{x} 构建的树Tree3的概率分布一致。因此,要计算插入或删除某个节点引起的树复杂度变化,只需将节点直接从树上插入或删除,而无需使用新的数据集来构建树[8]。这是RRCF适用于数据实时处理的理论依据。
1.2 RRCF异常检测若RRCF复杂度随着点的加入而显著增加,则该点为异常点。将某个样本点删除或插入后,模型的复杂度变化量(如所有叶子节点深度之和的变化量)为该点的异常程度。
给定样本点集S和样本点y(y∈S),定义f(y, S, T)为y在随机分割树T上的路径长度。删除点x后产生的树为T(S-{x}),此时,y在树T(S-{x})上的路径长度为f(y, S-{x}, T(S-{x}))。将树中所有点的路径长度之和定义为随机分割树的复杂度|M(T)|=∑f(y, S, T), y∈S,则将点x删除后,RRCF复杂度变化可表示为[8]:
| $ \begin{gathered} \mathscr{E}_{T(S)}[|M(T)|]-\mathscr{E}_{T(S-\{x\})}[|M(T(S-\{x\}))|]= \\ \sum\limits_T \sum\limits_{y \in S-\{x\}} P_r(T) \cdot(f(y, S, T)-\\ \left.f\left(y, S-\{x\}, T^{\prime}\right)\right)+ \\ \sum\limits_T P_r(T) \cdot f(y, S, T) \end{gathered} $ | (1) |
式中,
为有效避免异常屏蔽现象所引起的漏检问题,在执行删除操作时并不只是删除点x,而是删除一个含有x的集合C(x∈C⊂S),此时集合C的异常得分将归因于C中所有点。基于此,使用共谋异常得分衡量点x的异常程度[8]:
| $ \begin{gathered} \operatorname{CODISP}(x, S, |S|)= \\ \underset{S, T}{\mathscr{E}}\left[\max _{x \in C \subset S} \frac{1}{|C|} \sum\limits_{y \in S-C}(f(y, S, T(S))-\right. \\ f(y, S-C, T(S-C)))] \end{gathered} $ | (2) |
式中,集合C称为共谋集合。C中点的个数,即共谋集合的大小n将影响算法对异常屏蔽现象的识别能力。若n过大,异常点所在共谋集合中正常点的异常评分偏高,易将正常值误判为异常值;若n过小,则单独删除某个含有异常点的共谋集合时,模型复杂度不会发生显著变化,可能会将异常值误判为正常值,从而造成漏检。因此,合理设置共谋集合的大小可以有效提高算法的稳健性和准确率。
RRCF算法利用新增数据引起的整体模型复杂度变化衡量其异常程度,实现对实时数据流的异常探测;通过对模型数据重复性随机分割获取统计特性,确保异常值识别的准确度;使用数据替换的方式代替逐次建模,实现对模型的动态维护,可显著提高处理效率,满足海量数据的快速处理与分析需求。
2 基于RRCF的GNSS位移数据异常识别与探测基于RRCF的GNSS监测位移数据异常实时检测算法主要分为模型构建和异常评估两个阶段[12],算法架构如图 1所示。
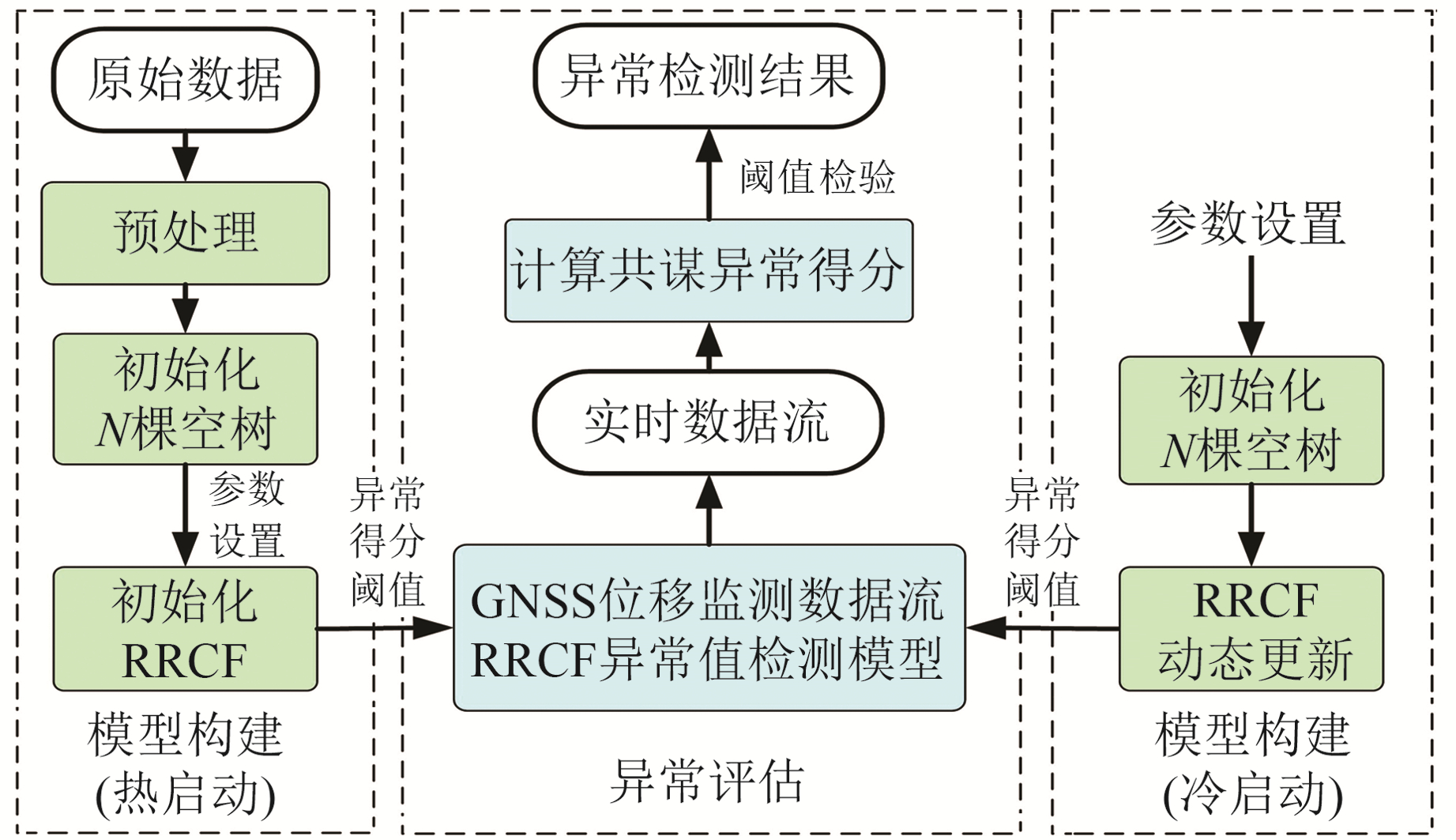
|
图 1 RRCF算法总体架构 Fig. 1 Architecture of RRCF algorithm |
若已有GNSS位移监测历史数据,则可使用历史数据对模型进行初始化,即热启动建模:
1) 输入RRCF异常值检测算法参数:随机分割树中样本个数n、随机分割森林中树的数量N、异常评分阈值T等;
2) 初始化创建N棵空树,结合训练数据集进行模型构建,并计算每个训练集样本点的共谋异常得分,将共谋异常得分与阈值T进行比较,判断该点是否为异常点。
若无可作为训练数据集的历史数据,则依靠实时数据流完成模型的初始化构建,即冷启动建模。与热启动不同,冷启动将实时数据流中待检测的点插入到N棵空树中,并计算共谋异常得分。若树中样本个数达到预设的样本个数n,随机选择一棵树,用待测点替换树中最旧的点,否则直接将待测点插入到树中。
2.2 异常评估阶段1) 根据实时GNSS位移监测数据流的RRCF异常值检测模型,用实时输入数据流中每个待测样本点替换树中最旧的点;
2) 使用RRCF异常值检测模型计算待测样本点的共谋异常评分,并与异常评分阈值进行比较,若大于阈值,则认为是异常数据,否则认为是正常数据。
3 实验验证与分析 3.1 模拟数据与结果分析 3.1.1 实验数据为验证算法的效果,采用GNSS位移分析中常用的坐标时间序列模型[13],模拟生成不含粗差的原始数据,函数表达式如下:
| $ \begin{gathered} x\left(t_i\right)=b+v_0 t_i+\sum\limits_{m=1}^{m_0}\left[a_m \sin \left(2 {\rm{ \mathsf{ π}}} f_m t_i\right)+\right. \\ \left.b_m \cos \left(2 {\rm{ \mathsf{ π}}} f_m t_i\right)\right]+r_{t_i} \end{gathered} $ | (3) |
式中,i为坐标历元时刻标识;x(ti) 为GNSS测站某分量ti时刻的坐标;b为截距;v0为线性速度;m0为谐波个数;am和bm表示频率为fm时周期项的振幅;rti为随机噪声,即rti∈N(0, σ2)。上述先验理论模型并不足以模拟受多种因素影响的GNSS监测位移序列的变化特征,因此分别基于理想先验模型和非理想先验模型生成2组不含粗差的原始数据。其中,理想先验模型生成的模拟数据参数为:b=5, v0=2, m0=2, a1=5, b1=5, a2=3, b2=3, σ=3,f1和f2分别表示周期为1 a和半年对应的频率;非理想先验模型生成的模拟数据中,另外加入高频周期项,其参数为a3=6,对应频率f3=7。
在模拟粗差数据时,首先采用标准差为3σ(σ为随机噪声标准差)的正态分布模拟得到一组随机误差序列,然后将大于3σ的误差序列随机加入到不含粗差的原始数据中,最终得到受粗差污染的GNSS位移时间序列[3]。实验数据由MATLAB平台生成,历元间隔4 h,共2 223个历元。模拟的粗差总数为140,占总观测历元的6.30%,实验数据如图 2所示。

|
图 2 实验数据 Fig. 2 Experimental data |
异常值检测效果通过准确率A、精确率P、召回率R以及综合评价指标F1进行评价:
| $ A=\left(n_{\mathrm{TP}}+n_{\mathrm{TN}}\right) /\left(n_{\mathrm{TP}}+n_{\mathrm{TN}}+n_{\mathrm{FP}}+n_{\mathrm{FN}}\right) $ | (4) |
| $ P=n_{\mathrm{TP}} /\left(n_{\mathrm{TP}}+n_{\mathrm{FP}}\right) $ | (5) |
| $ R=n_{\mathrm{TP}} /\left(n_{\mathrm{TP}}+n_{\mathrm{FN}}\right) $ | (6) |
| $ F_1=2 P \cdot R /(P+R) $ | (7) |
式中,nTP、nTN、nFP、nFN分别表示正常点检测为正常、异常点检测为异常、异常点检测为正常、正常点检测为异常的样本点个数。准确率可衡量算法预测正确的结果占总样本的百分比;精确率可描述所有被预测为正常的样本中实际为正常样本的概率,可反映算法对异常值的误判率;召回率可描述实际为正常的样本被预测为正常样本的概率,可反映算法对正常值的误判率;综合评价指标F1为综合精确率和召回率对算法效果的整体评价。
3.1.3 结果分析利用小波-3σ方法[3]和RRCF实时异常检测方法对2组实验数据进行处理与分析。其中,小波-3σ方法依据经验选取变形分析中常用的sym7小波基函数,通过筛选确定分解层次为6;RRCF方法采用模拟实时数据处理的策略,使用前300组数据进行建模,剩余数据递次送入模型进行检验,判断是否存在异常。
理想先验模型实验数据处理结果如图 3所示,由图可知,小波-3σ方法可以探测出GNSS变形序列中的大部分粗差,RRCF实时粗差探测效果与事后小波-3σ方法相当。非理想先验模型实验数据处理结果如图 4所示,由图可知,相较于理想先验模型实验数据处理结果,2种方法均可探测出大部分粗差,但漏检个数明显增多。同时,小波-3σ方法略优于RRCF方法。

|
图 3 理想先验模型实验数据粗差探测结果 Fig. 3 Gross error detection results of experimental data generated by the ideal prior model |

|
图 4 非理想先验模型实验数据粗差探测结果 Fig. 4 Gross error detection results of experimental data generated by the non-ideal prior model |
表 1为2种方法粗差探测结果统计,由表可知,在理想先验模型仿真数据条件下,相较于小波-3σ方法,RRCF方法的检测异常数和漏检个数较多,准确率和精确率略低,但召回率和总体评价指标略高。由召回率可知,RRCF方法在理想先验模型中将正常值误判为异常值的概率较低。在非理想先验模型仿真数据条件下,相较于小波-3σ方法,RRCF方法的检测异常数和漏检个数较多,准确率、精确率、召回率和总体评价指标均略低。与小波-3σ方法相比,RRCF方法更适用于缓变的GNSS位移监测序列的异常值检测。小波-3σ方法在两种条件下的总体评价指标F1分别为0.967 3和0.994 0,RRCF方法分别为0.975 7和0.976 8。对理想先验模型仿真数据而言,RRCF方法略优于小波-3σ方法;而在非理想先验模型仿真数据条件下,RRCF方法略低于小波-3σ方法。
|
|
表 1 粗差探测结果统计 Tab. 1 Statistics of gross error detection |
RRCF算法作为一种实时异常检测方法,仅依据当前历元收集的数据对下个历元数据进行异常判断,对异常点识别的准确率、精确率与召回率接近事后方法,可以满足海量实时数据流的异常探测需求。
3.2 工程案例结果与分析黑台滑坡位于甘肃省永靖县盐锅峡镇,使用该滑坡05GP01测站2019-11-01~2021-10-25实测GNSS位移监测数据,样本个数为9 589个。原始数据包含水平位移、垂直位移与合位移,本文将以垂直位移处理结果为例进行详细分析。
图 5(a)为垂直方向GNSS位移监测原始数据,红色方框中数据点为明显的离群异常点。对数据进行划分,取前1 000组数据为训练集对随机分割森林进行初始化,剩余数据作为测试集。数据测试结果表明,随机分割树的最大容量取256、512和1 024时影响不大,本文设置为256;共谋集合大小依据经验取为5,既不会将粗差值湮没,也可避免因捕捉噪声导致误警。对大量实测GNSS位移监测数据进行处理,结果表明,异常评分阈值设置为50时符合大多数GNSS累积位移监测数据粗差检测的实际需要。
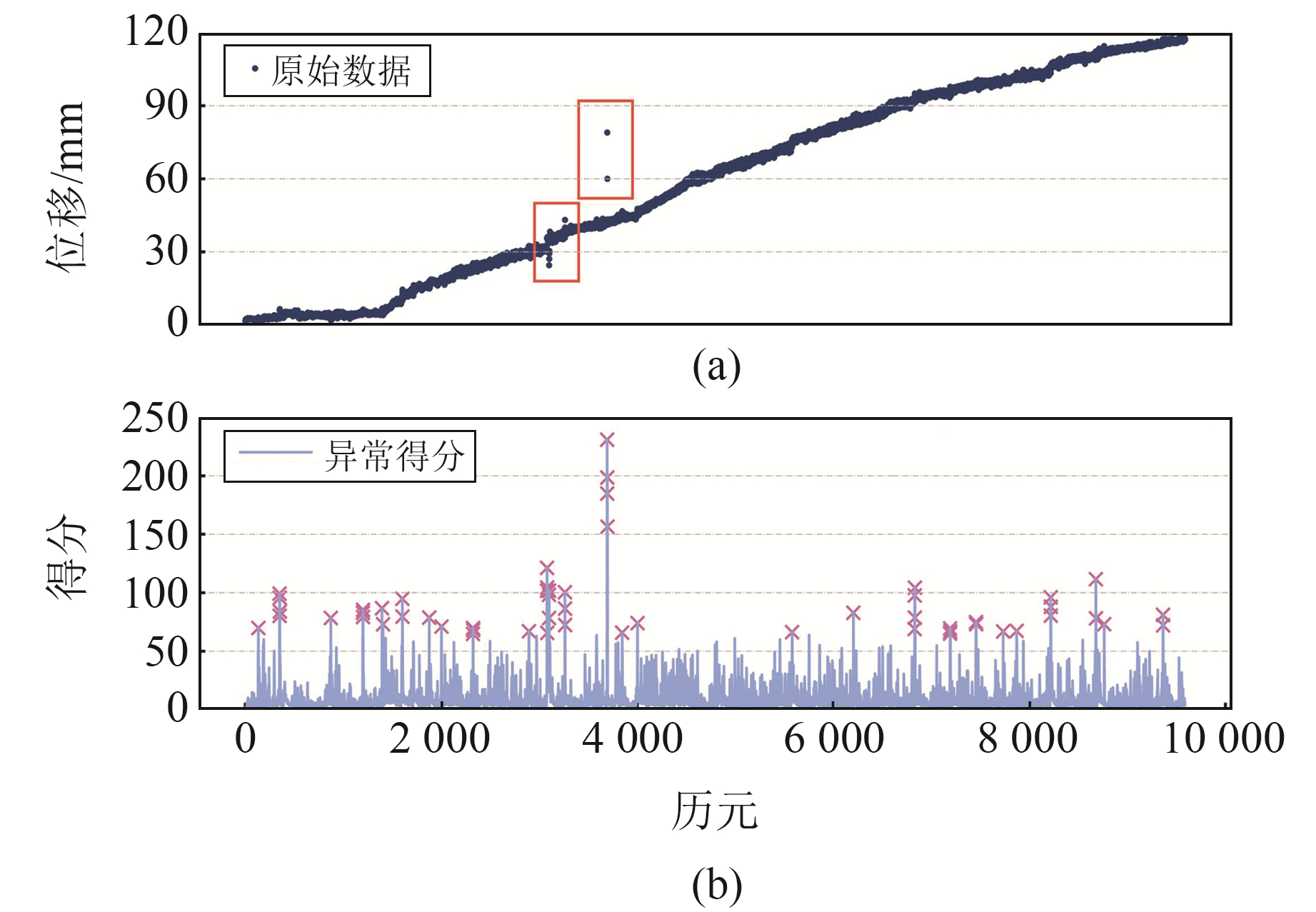
|
图 5 RRCF方法异常评分 Fig. 5 Anomaly score of RRCF method |
图 5(b)为实时数据的异常得分,将异常得分与阈值进行比较,可筛选出异常值。最终在9 589个样本中检测出60个异常值,GNSS位移数据异常值识别效果与删除异常值之后的正常数据如图 6(a)和6(b)所示。由图可知,GNSS位移监测数据发生异常突变时,RRCF方法可以很好地识别异常值,其检测结果与实际异常值情况吻合且误判率较低。上述结果表明,基于RRCF的GNSS位移监测数据异常实时检测算法具有可行性,且对实时动态变化的数据流具有很好的适应性。
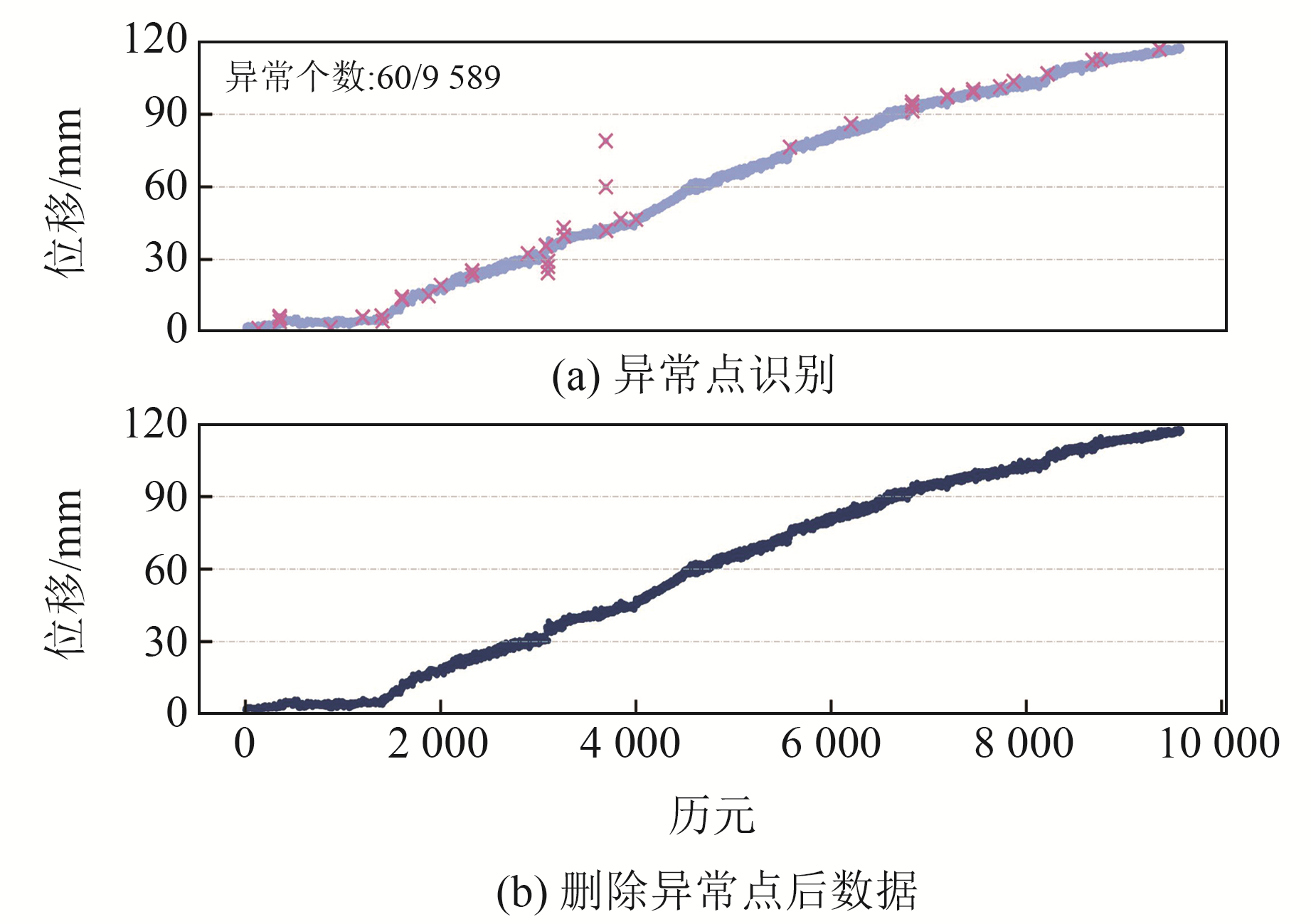
|
图 6 原始GNSS位移监测数据及RRCF方法粗差探测结果 Fig. 6 Original GNSS displacement monitoring data and gross error detection results of RRCF method |
为进一步验证RRCF实时算法粗差探测的准确性,使用小波-3σ方法对该数据进行事后异常检测。图 7(a)为异常点探测情况,将异常点删除后的正常数据如图 7(b)所示。小波-3σ方法在9 589个样本中检测出77个异常值,由图 7可知,该方法可识别并剔除大部分异常点。
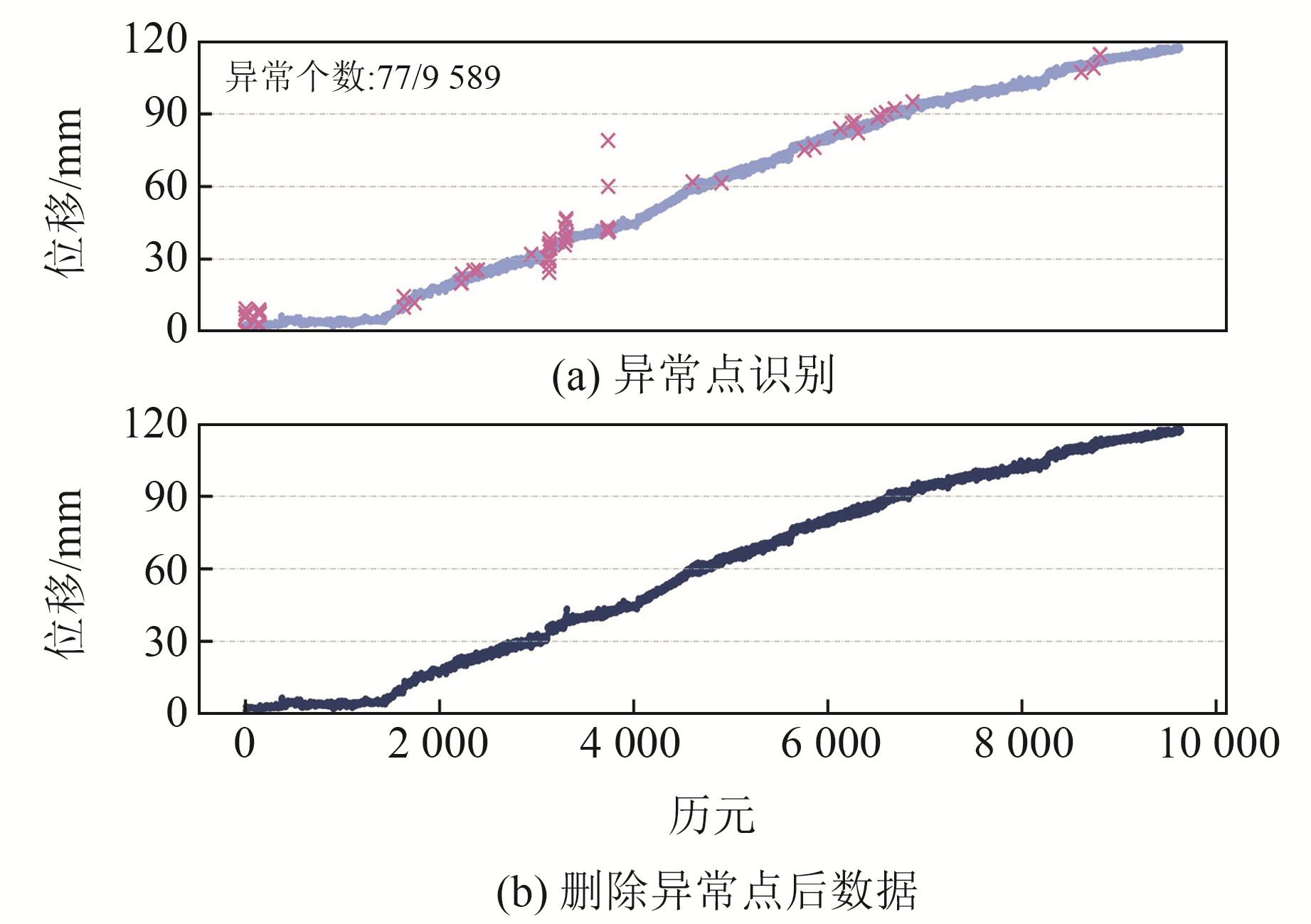
|
图 7 原始GNSS位移监测数据及小波-3σ方法粗差探测结果 Fig. 7 Original GNSS displacement monitoring data and gross error detection results of wavelet-3σ method |
小波-3σ方法利用小波分解出的高频系数计算得到观测数据的中误差估值σ[3],容易受到小波分解的趋势项与实际变形特征的符合程度、粗差大小及分布的影响和干扰,导致求取的中误差估值不准确,进而影响粗差探测效果。因此,小波-3σ方法容易因小波基和分解层数设置不合理而出现误判或漏判。实时RRCF方法根据数据插入或删除后模型的复杂度变化来衡量数据异常程度,可根据数据实时变化特征进行灵活调整,且评分标准统一,不易受到数据特征的影响,可适用于GNSS位移数据的实时监测。
在GNSS位移粗差实时检测过程中,若水平方向位移、垂直方向位移与合位移均发生异常,则应注意该测站其他传感器或该滑坡体的其他测站是否也同时出现警报,综合判断是否发布地质灾害预警。
4 结语本文提出基于RRCF的GNSS位移监测数据异常实时检测方法,同时采用仿真数据与实测数据对算法进行验证与分析,得到以下结论:RRCF方法在理想先验模型条件下略优于小波-3σ方法,准确率和精确率略低,召回率略高,异常检测的总体评价指标F1为0.975 7;而在非理想先验模型仿真数据条件下,RRCF方法略差于小波-3σ方法,准确率、精确率、召回率均略低,总体评价指标为0.976 8。针对数据异常实时检测场景,采用地质灾害位移监测数据进行验证,结果表明GNSS位移监测数据发生异常突变时,RRCF方法可以很好地识别异常值,其检测结果与实际异常值情况吻合且误判率较低,具有较高的检测准确率和可用性,可为GNSS位移实时监测预警提供技术支撑。
| [1] |
黄凯, 陈渠森, 鞠博晓. GNSS自动化监测系统的大坝变形预测方法研究[J]. 测绘通报, 2018(1): 147-150 (Huang Kai, Chen Qusen, Ju Boxiao. Study on Prediction Method of Dam Deformation for GNSS Automatic Monitoring System[J]. Bulletin of Surveying and Mapping, 2018(1): 147-150)
(  0) 0) |
| [2] |
张鸣之, 湛兵, 赵文祎, 等. 基于虚拟参考站技术的滑坡高精度位移监测系统设计与实践[J]. 中国地质灾害与防治学报, 2020, 31(6): 54-59 (Zhang Mingzhi, Zhan Bing, Zhao Wenyi, et al. Design and Practice of High Precision Landslide Displacement Monitoring System Based on VRS[J]. The Chinese Journal of Geological Hazard and Control, 2020, 31(6): 54-59)
(  0) 0) |
| [3] |
吴浩, 卢楠, 邹进贵, 等. GNSS变形监测时间序列的改进型3σ粗差探测方法[J]. 武汉大学学报: 信息科学版, 2019, 44(9): 1 282-1 288 (Wu Hao, Lu Nan, Zou Jingui, et al. An Improved 3σ Gross Error Detection Method for GNSS Deformation Monitoring Time Series[J]. Geomatics and Information Science of Wuhan University, 2019, 44(9): 1 282-1 288)
(  0) 0) |
| [4] |
张东华, 李志娟, 刘全明, 等. 奇异谱分析的变形监测序列粗差探测方法[J]. 测绘科学, 2020, 45(8): 14-18 (Zhang Donghua, Li Zhijuan, Liu Quanming, et al. The Gross Error Detection of Dam Deformation Observation Data Based on Singular Spectrum Analysis[J]. Science of Surveying and Mapping, 2020, 45(8): 14-18)
(  0) 0) |
| [5] |
李喜盼, 扈静, 李海刚. 基于小波分析的GPS动态变形数据粗差识别模型研究[J]. 测绘通报, 2011(4): 7-9 (Li Xipan, Hu Jing, Li Haigang. Research on Model of Gross Error Identification for GPS Dynamic Deformation Data Based on Wavelet Analysis[J]. Bulletin of Surveying and Mapping, 2011(4): 7-9)
(  0) 0) |
| [6] |
Hua C, Zhang Q, Xu G H, et al. Performance Reliability Estimation Method Based on Adaptive Failure Threshold[J]. Mechanical Systems and Signal Processing, 2013, 36(2): 505-519 DOI:10.1016/j.ymssp.2012.10.019
(  0) 0) |
| [7] |
Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1 735-1 780 DOI:10.1162/neco.1997.9.8.1735
(  0) 0) |
| [8] |
Guha S, Mishra N, Roy G, et al. Robust Random Cut Forest Based Anomaly Detection on Streams[C]. Proceedings of the 33rd International Conference on Machine Learning, New York, 2016
(  0) 0) |
| [9] |
Bartos M, Mullapudi A, Troutman S. RRCF: Implementation of the Robust Random Cut Forest Algorithm for Anomaly Detection on Streams[J]. The Journal of Open Source Software, 2019, 4(35)
(  0) 0) |
| [10] |
Inoue J, Yamagata Y, Chen Y Q, et al. Anomaly Detection for a Water Treatment System Using Unsupervised Machine Learning[C]. IEEE International Conference on Data Mining Workshops(ICDMW), New Orleans, 2017
(  0) 0) |
| [11] |
Wang Y, Wang Z W, Xie Z J, et al. Practical and White-Box Anomaly Detection through Unsupervised and Active Learning[C]. 29th International Conference on Computer Communications and Networks(ICCCN), Honolulu, 2020
(  0) 0) |
| [12] |
张国芳, 温丽丽, 吴蒙, 等. 基于鲁棒性随机分割森林算法的变压器损耗异常值检测[J]. 华东师范大学学报: 自然科学版, 2021(6): 135-146 (Zhang Guofang, Wen Lili, Wu Meng, et al. Anomaly Detection of Transformer Loss Data Based on a Robust Random Cut Forest[J]. Journal of East China Normal University: Natural Science, 2021(6): 135-146)
(  0) 0) |
| [13] |
黄立人, 韩月萍, 高艳龙, 等. GNSS连续站坐标的高程分量时间序列在地壳垂直运动研究中应用的若干问题[J]. 大地测量与地球动力学, 2012, 32(4): 10-14 (Huang Liren, Han Yueping, Gao Yanlong, et al. Several Issues in Application of Elevation Component Time Series of GNSS CORS in Vertical Crustal Movement Studying[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 10-14)
(  0) 0) |
2. China Institute of Geo-Environment Monitoring, 20 Dahuisi, Beijing 100081, China;
3. Technology Innovation Center for Geohazard Monitoring and Risk Early Warning, MNR, 20 Dahuisi, Beijing 100081, China;
4. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
5. School of Information Engineering, China University of Geosciences, 29 Xueyuan Road, Beijing 100083, China;
6. School of Geography and Information Engineering, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China
 2024, Vol. 44
2024, Vol. 44


