2. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077
前人根据地震同震形变反演断层参数时,为了简化模型,常常会忽略真实地形因素。在计算同震形变时地表真实地形会产生多大影响至今仍然不明确,部分学者认为地形效应对同震形变影响较大[1-3],但也有学者持相反意见[4-6]。
2013-04-20四川芦山发生MS7.0地震,震中位于四川盆地西缘。四川盆地平均海拔为250~750 m,而青藏高原平均海拔为3 000~5 000 m,地形梯度变化较大,因此此次地震是研究地形对地震同震形变影响的较好案例。谱元法(spectral element method, SEM)可兼顾有限元法网格的灵活性和伪谱法的高精度、快速收敛特性,在复杂地震动数值模拟方面得到广泛应用[7-9]。本文利用谱元法模拟2013年芦山MS7.0地震同震形变,探讨地形对地表同震形变的影响。
1 谱元法计算同震形变 1.1 控制方程在图 1所示设置中求解控制同震形变的准静态方程。计算区域Ω被嵌入在准半空间中,包括自由表面Γ0和人工边界Γ,半空间包括自由表面Γ0和Γ∞。

|
图 1 准半空间中断层示意图 Fig. 1 Schematic diagram of fault in a quasi-half space |
区域Ω的控制方程可表示为:
| $ \nabla \cdot T+f=0 $ | (1) |
式中,T为应力张量,f为外力。
在自由表面Γ0上满足边界条件:
| $ \hat{\boldsymbol{n}} \cdot T=0 $ | (2) |
同震形变由弹性本构关系T=c: ε控制,c为4阶弹性张量,ε为应变张量。
1.2 分裂节点法地震震源由断层面Σ上的滑动矢量Δs定义。如图 1所示,当从断层Σ的正侧向负侧移动时,滑动矢量捕获到位移场 s的不连续性[10]:
| $ \Delta \boldsymbol{s}=\boldsymbol{s}^{+}-\boldsymbol{s}^{-}=[\boldsymbol{s}]_{-}^{+} $ | (3) |
式中,[·]-+表示捕获断层从正侧到负侧封闭量的跃变。对于滑动断层,位移的法向分量在断层上必须连续,即
本文采用分裂节点法对模型域进行网格划分,使元素边界满足断层面[11](图 2)。在分裂节点法中,通过在断层面上规定一个不连续的位移场来引入载荷,因此控制方程(1)中f为0。

|
图中使用谱元素(浅灰色单元)离散化研究区域Ω,在区域外添加一层无限元素(深灰色单元);黑色粗实线表示断层 图 2 分裂节点法网格划分示意图 Fig. 2 Schematic diagram of grid division using split node method |
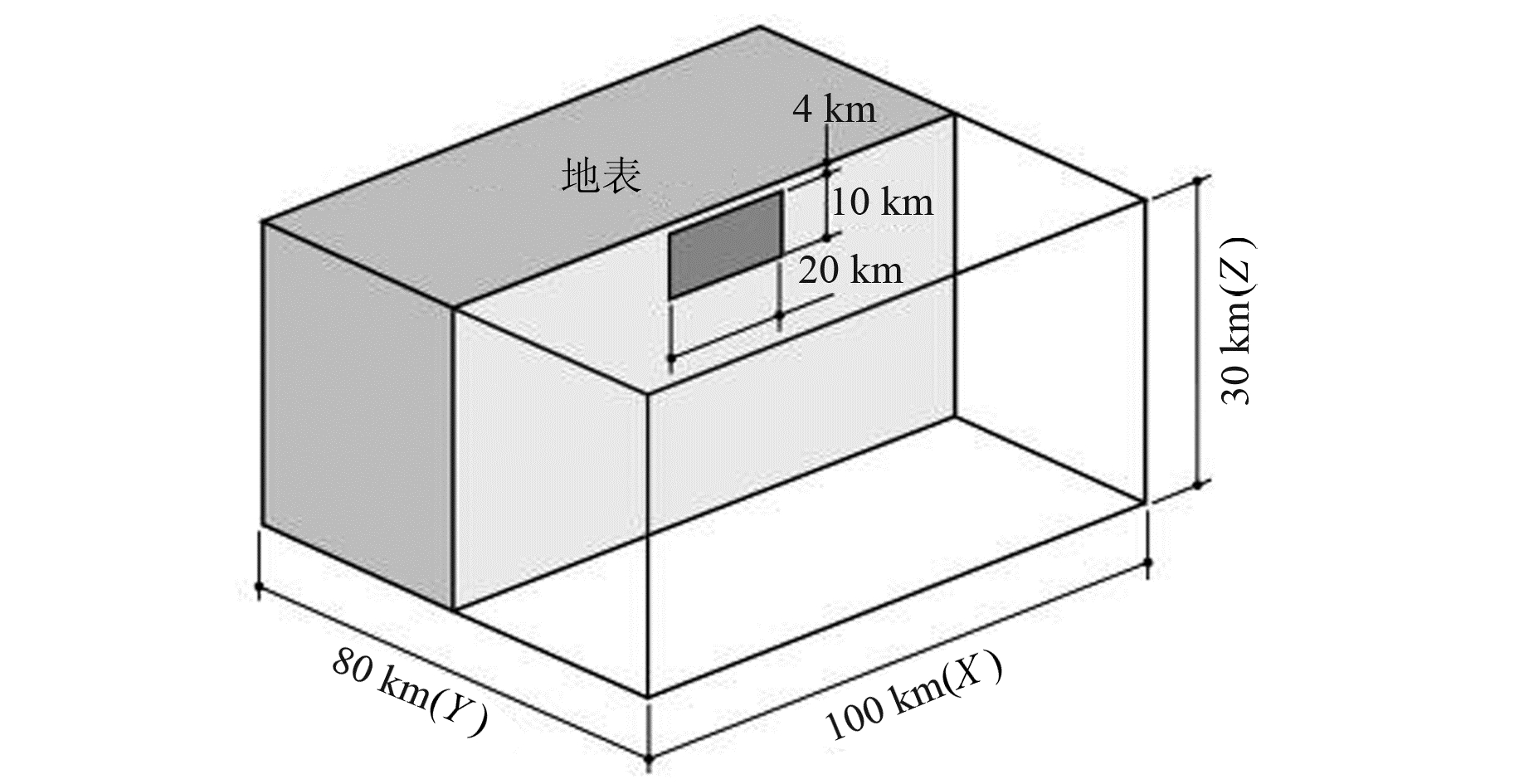
通过模拟基于弹性半空间各向同性介质的垂直断层走滑和倾滑,验证谱元法在地震同震形变模拟中的可靠性。采用图 3所示模型,尺寸为100 km×80 km×30 km,泊松比为0.25,杨氏弹性模量为5.68 GPa。图中深灰色矩形表示断层,其顶部距离地表 4 km,底部距离地表 14 km,中心距离模型左右两侧边界50 km。使用近似为2 km×2 km×2 km的六面体单元对模型进行网格划分,共包含30 000个单元和253 611个节点,节点自由度为725 370。模型顶面施加应力自由边界条件,侧边和底面施加Dirichlet边界条件。
|
图 3 垂直断层模型 Fig. 3 Vertical fault model |
设定断层右旋纯走滑量为4 m,并使用谱元法计算地表三维同震形变,将数值模拟结果与Okada解析法结果进行对比(图 4)。从图 4(a)和4(b)可以看出,采用2种方法计算得到的水平位移场沿断层两侧呈反对称分布,靠近断层位置的水平位移较大且与断层走向平行。从图 4(c)和4(d)可以看出,采用2种方法计算得到的垂直位移场呈四象限对称分布。水平和垂直位移场的分布均符合右旋走滑断层特征,并且谱元法与Okada解析法结果在数值上具有很好的一致性。

|
粗黑直线代表断层所在位置,红色箭头代表断层走向 图 4 走滑断层引起的地表三维同震形变场分布 Fig. 4 Distribution of three-dimensional coseismic surface deformation caused by strike-slip fault |
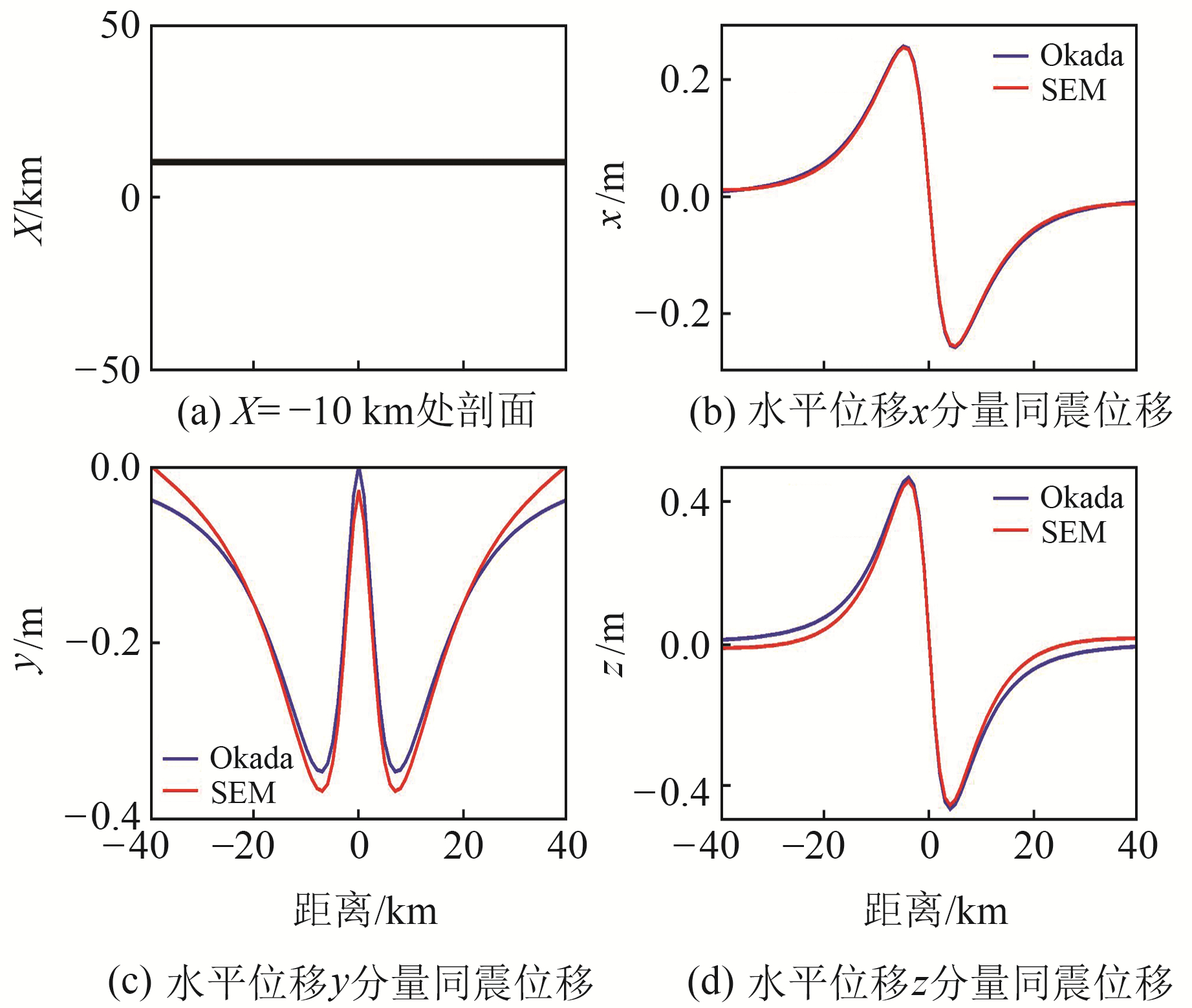
为详细研究谱元法与Okada解析法的差异,选择位移场剖面X=-10 km位置,将2种方法的模拟结果进行对比。从图 5可以看出,对于水平位移x分量,除边界区域外,两者的振幅和相位基本一致。对于水平位移y分量,在断层附近,左侧Okada解析法结果大于谱元法,右侧谱元法结果大于Okada解析法;而在超过7 km之后,Okada解析法结果大于谱元法。对于垂直位移z分量,在断层附近,谱元法结果大于Okada解析法。总体而言,两者差异最大不超过10%。

|
图 5 走滑断层在X=-10 km处地表位移剖面 Fig. 5 Surface displacement profile of strike-slip fault at X=-10 km |
设定断层纯倾滑量为4 m,同样采用上节中所构建的模型区域和介质属性。对比谱元法结果与Okada解析法结果(图 6)可知,水平和垂直位移场的分布均符合断层倾滑特征,并且谱元法与Okada解析法结果在数值上具有很好的一致性。

|
粗黑实线代表断层所在位置,红色圆圈和叉代表断层倾向 图 6 倾滑断层引起的地表三维同震形变场分布 Fig. 6 Distribution of three-dimensional coseismic surface deformation caused by dip-slip fault |
选取X=10 km地表位移剖面,对比谱元法数值模拟结果与Okada解析法结果。由图 7可知,x和z分量呈中心对称分布,y分量呈轴对称分布。靠近断层时,2种方法所有分量的振幅和相位吻合较好;远离断层时,2种方法所有分量均存在一定差异,这可能是由建模误差或数值方法的近似性所致。在下一步研究中,将考虑添加无限元素以更好地探究这些差异的原因。
|
图 7 倾滑断层在X=10 km处地表位移剖面 Fig. 7 Surface displacement profile of dip-slip fault at X=10 km |
综合走滑运动和倾滑运动数值模拟结果可知,谱元法与Okada解析法计算结果一致性良好。因此,认为使用谱元法模拟地震地表同震形变具有可行性。
3 地形因素对2013年芦山MS7.0地震同震形变的影响 3.1 数据本文使用的GPS同震位移资料来自于33个GPS连续站,GPS观测数据最大水平误差小于3 mm,最大垂直误差小于12.4 mm[12]。图 8为本文研究区,震源中心位于30.3°N、103.0°E。使用单一平面断层生成格林函数,断层参数参照Duan等[13]的研究成果。

|
图中沙滩球为CENC CMT震源机制解;红色五角星为震中位置;U-V为谱元法计算时所采用的坐标系,U为沿断层走向方向,V为垂直断层走向方向 图 8 芦山地震构造背景 Fig. 8 Tectonic background of the Lushan earthquake |
将芦山地区真实地表-地壳结构纳入模型中,地形网格文件使用NOAA发布的ETOPO1数据[14],分辨率为1′,包含陆地地形和海洋水深数据。模型介质参数参考谈洪波等[15]的研究成果。
3.2 模型构建为研究地形因素对同震形变的影响,构建图 9中2种模型,其中A为地形模型(图 9(a)),B为无地形模型(图 9(b))。本文模型基于均匀弹性介质,泊松比为0.25,杨氏弹性模量为79.8 GPa,水平尺寸为116 km×133 km,深度为40 km(不包括地形)。离散模型使用六面体单元,所有模型平均网格间距设置为2 km,模型A共包含79 750个单元和675 608个节点,模型B共包含81 200个单元和686 868个节点。

|
粉红色矩形为断层位置;U为沿断层走向方向,V为沿垂直断层走向方向 图 9 芦山地震同震形变介质模型 Fig. 9 Medium models for coseismic deformation of the Lushan earthquake |
2013年芦山MS7.0地震是发生在龙门山断裂带西南段的一次浅源逆冲型地震,破裂长度20 km[16],地震引起明显的地表水平位移及垂直形变,可为研究地形效应对同震形变的影响提供理想的条件。
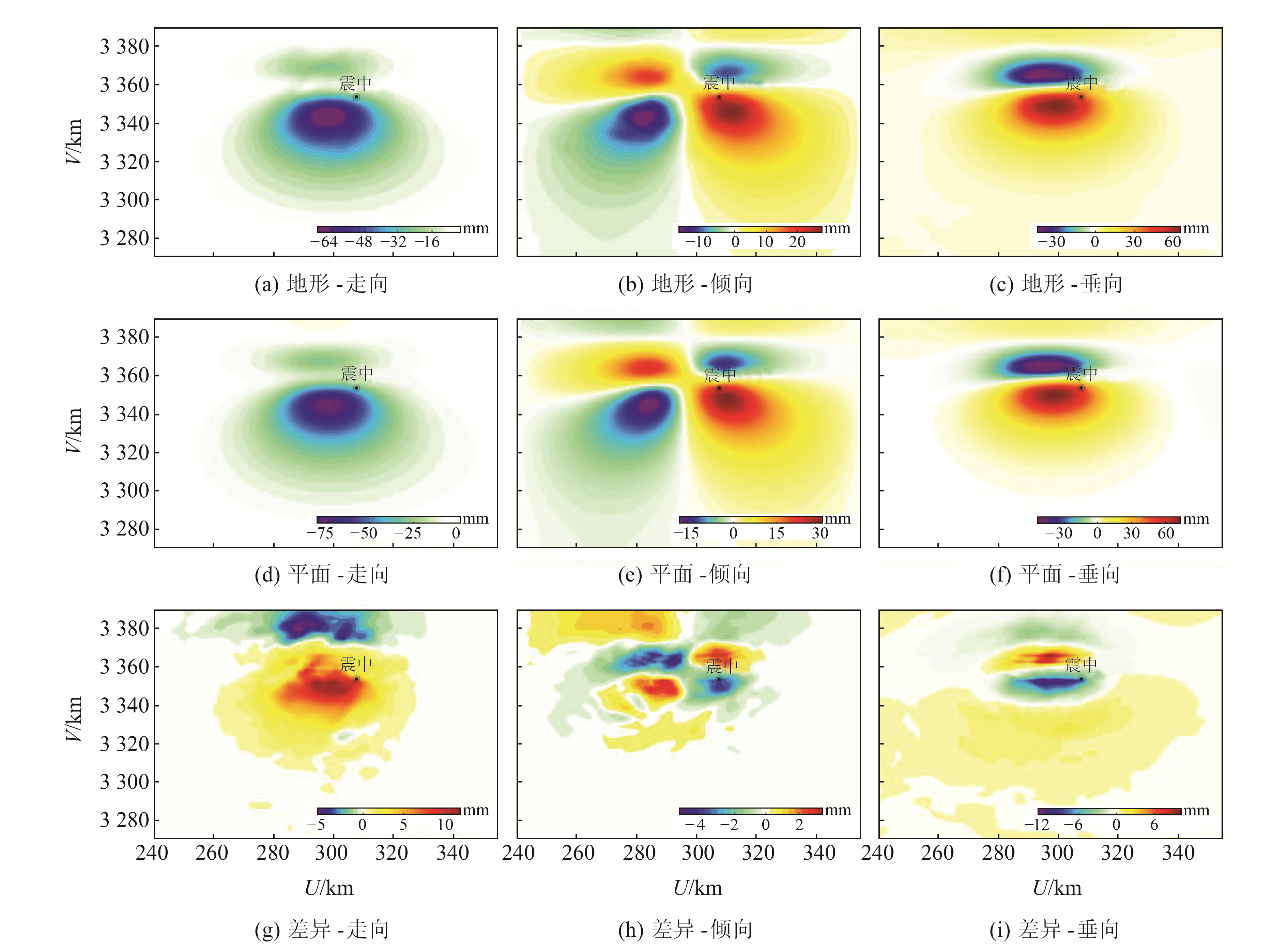
本文分别基于模型A和模型B,利用谱元法计算地表同震位移,并探讨地形对地表同震位移的影响。图 10为2种模型生成的地表同震位移场,可以看出,模型A计算的沿断层走向方向位移为-71~0 mm, 垂直断层走向方向位移为-18~28 mm, 垂直方向位移为-42~67 mm;模型B则分别为-80~2.5 mm、-19~31 mm和-47~75 mm。由图 9可知,同震形变场分布形态符合逆冲型地震特征,距离震中越近,同震形变越大。地形的存在不仅会改变地表同震形变场分布形态,也会改变同震位移的大小。从图 10(a)和10(d)可以看出,在震中上方区域,模型A形变场分布不如模型B平滑,且模型A的最大值比模型B少9 mm,对比图 10(b)与10(e)、10(c)与10(f),也有类似的情况。
|
第1、2行分别为基于模型A、B计算的同震位移,第3行为模型A与模型B之差;第1、2、3列分别代表沿断层走向的水平位移、垂直断层走向的水平位移、垂直位移 图 10 不同模型的地表同震位移 Fig. 10 Coseismic surface displacements of different models |
本文利用林晓光等[3]的方法计算地形效应的影响。结果表明,沿断层走向方向、垂直断层走向方向和垂直方向,地形对同震形变的影响最大可达约16.8%、19.2%和18.3%。
4 讨论本文基于平面断层模型研究地形对同震形变的影响,断层参数在一定程度上会影响地表同震位移,这里主要讨论断层倾角和深度对地表同震位移的影响。
在Duan等[13]的研究结果基础上,构建6种模型,采用控制变量法研究断层倾角和深度对地表同震位移的影响,所有模型使用与§3.2相同的介质参数。数值模拟结果如表 1、2所示。
|
|
表 1 不同倾角下计算的同震位移 Tab. 1 Coseismic displacements calculated by different dip angles |
|
|
表 2 不同深度下计算的同震位移 Tab. 2 Coseismic displacements calculated by different depths |
根据所选研究区域,使用8个GPS站点观测值,为了与谱元法结果进行对比,将这些GPS观测值转换到U-V坐标系下(谱元法计算时所采用的坐标系),沿断层走向方向U分量变化范围为-63.8~2.4 mm,沿垂直断层走向方向V分量变化范围为-17.6~22.1 mm,垂直方向Z分量变化范围为-4.9~83.6 mm。
通过表 1可以看出,随着断层倾角增大,沿断层走向方向分量、垂直断层走向方向分量和垂直方向分量位移均减小。
由表 2可知,随着断层深度变浅,地表同震位移逐渐变大。这是因为浅层断层距离地表更近,断层运动能更直接地影响地表,从而使地表同震形变更为明显。
在原始断层几何参数基础上,将断层走滑分量和倾滑分量分别设置为0.15 m和0.70 m,计算得到地形效应对沿断层走向方向同震形变的影响最大可达约10.3%,对垂直断层走向方向同震形变的影响最大可达约12.4%。这与Lin等[2]计算汶川地震地形效应对同震位移的影响(9.05%)不同,可能是由于其使用的是二维有限元模型,而本文采用的是三维谱元法模型。Langer等[1]计算智利地震地形效应对同震位移的影响为30%,远大于本文计算值,这可能是由于秘鲁-智利海沟地形急剧变化,相对高差过大,而且断层两侧介质不同,一侧为海域,而另一侧为陆地。
值得一提的是,GPS结果是某一确定点的形变数据,而谱元法结果是整个网格区域的形变情况。为了方便二者对比,谱元法结果使用与GPS观测点邻近区域的位移值。本文选取同震区域位移较大的LS05、LS07、SCTQ测站进行对比。LS05测站东、北分量观测值分别为-9.9 mm、-66.8 mm,谱元法模拟值分别为-10.4 mm、-53.3 mm;LS07测站东、北分量观测值分别为24.1 mm、-17.8 mm,谱元法模拟值分别为17.1 mm、-17.0 mm;SCTQ测站东、北分量观测值分别为-9.8 mm、-18.7 mm,谱元法模拟值分别为-7.0 mm、-20.1 mm。除LS05测站北分量差异较大外(13.5 mm),其他结果二者较为接近。
5 结语在不考虑地形条件下,采用谱元法与Okada解析法分别计算垂直断层走滑、倾滑运动引起的地表同震位移。结果表明,无论对于走滑断层还是倾滑断层,2种方法结果的一致性均较好,表明谱元法模拟同震形变具有可靠性。
针对2013-04-20芦山MS7.0地震,本文分别构建芦山区域地形模型和无地形模型,探讨地形效应对同震形变的影响。结果表明,地形因素不仅会改变地表位移场分布形态,而且量值在不同方向上也有所差异。对于水平同震形变分量而言,沿断层走向和垂直断层走向的影响最大分别约为10.3%、12.4%;对于垂直同震形变分量而言,最大影响可达约11.9%。反演此次地震断层滑动速率时,若不考虑地形因素的影响,计算结果会低估断层走滑分量和高估倾滑分量。
本文基于平面断层几何模型探究地形对地震同震形变的影响,然而芦山地区断层几何复杂,为了更全面地理解同震形变的影响,后续将进一步收集同震DInSAR数据,并考虑更精细的断层几何模型,以便更准确地研究地形对同震形变的影响。另外,对于复杂的断层几何模型,不同构建方法所得结果的差异也值得进一步探索。
致谢: 感谢Gharti教授提供SPECFEM-X软件。
| [1] |
Langer L, Gharti H N, Tromp J. Impact of Topography and Three-Dimensional Heterogeneity on Coseismic Deformation[J]. Geophysical Journal International, 2019, 217(2): 866-878 DOI:10.1093/gji/ggz060
(  0) 0) |
| [2] |
Lin X G, Sun W K, Zhang H, et al. A Feasibility Study of an FEM Simulation Used in Co-Seismic Deformations: A Case Study of a Dip-Slip Fault[J]. Terrestrial, Atmospheric and Oceanic Sciences, 2013, 24(4): 637-647
(  0) 0) |
| [3] |
林晓光, 孙文科. 地形效应和局部地质构造对计算同震形变的影响——以2011年日本东北大地震(MW9.0)为例[J]. 地球物理学报, 2014, 57(8): 2 530-2 540 (Lin Xiaoguang, Sun Wenke. Effects of Topography and Local Geological Structure on Computing Co-Seismic Deformation——A Case Study of the 2011 Japan Tohoku Earthquake(MW9.0)[J]. Chinese Journal of Geophysics, 2014, 57(8): 2 530-2 540)
(  0) 0) |
| [4] |
Masterlark T. Finite Element Model Predictions of Static Deformation from Dislocation Sources in a Subduction Zone: Sensitivities to Homogeneous, Isotropic, Poisson-Solid, and Half-Space Assumptions[J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B11)
(  0) 0) |
| [5] |
Trasatti E, Kyriakopoulos C, Chini M. Finite Element Inversion of DInSAR Data from the MW6.3 L'Aquila Earthquake, 2009(Italy)[J]. Geophysical Research Letters, 2011, 38(8)
(  0) 0) |
| [6] |
Williams C A, Wallace L M. The Impact of Realistic Elastic Properties on Inversions of Shallow Subduction Interface Slow Slip Events Using Seafloor Geodetic Data[J]. Geophysical Research Letters, 2018, 45(15): 7 462-7 470 DOI:10.1029/2018GL078042
(  0) 0) |
| [7] |
Komatitsch D, Tsuboi S, Tromp J. The Spectral-Element Method in Seismology[M]//Levander A, Nolet G. Seismic Earth: Array Analysis of Broadband Seismograms. Washington D C: American Geophysical Union, 2005
(  0) 0) |
| [8] |
Seriani G. A Parallel Spectral Element Method for Acoustic Wave Modeling[J]. Journal of Computational Acoustics, 1997, 5(1): 53-69 DOI:10.1142/S0218396X97000058
(  0) 0) |
| [9] |
Komatitsch D, Vilotte J P. The Spectral Element Method: An Efficient Tool to Simulate the Seismic Response of 2D and 3D Geological Structures[J]. Bulletin of the Seismological Society of America, 1998, 88(2): 368-392 DOI:10.1785/BSSA0880020368
(  0) 0) |
| [10] |
Aki K, Richards P G. Quantitative Seismology: Theory and Methods[M]. San Francisco: Freeman W H and Company, 1980
(  0) 0) |
| [11] |
Melosh H J, Raefsky A. A Simple and Efficient Method for Introducing Faults into Finite Element Computations[J]. Bulletin of the Seismological Society of America, 1981, 71(5): 1 391-1 400
(  0) 0) |
| [12] |
Jiang Z S, Wang M, Wang Y Z, et al. GPS Constrained Coseismic Source and Slip Distribution of the 2013 MW6.6 Lushan, China, Earthquake and Its Tectonic Implications[J]. Geophysical Research Letters, 2014, 41(2): 407-413 DOI:10.1002/2013GL058812
(  0) 0) |
| [13] |
Duan H R, Chen J Y, Zhang S C, et al. Coseismic Fault Slip Inversion of the 2013 Lushan MS7.0 Earthquake Based on the Triangular Dislocation Model[J]. Scientific Reports, 2022, 12(1)
(  0) 0) |
| [14] |
Amante C, Eakins B W. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis[R]. NOAA, 2009
(  0) 0) |
| [15] |
谈洪波, 申重阳, 玄松柏. 地壳分层和地壳厚度对汶川地震同震效应的影响[J]. 大地测量与地球动力学, 2010, 30(4): 29-35 (Tan Hongbo, Shen Chongyang, Xuan Songbai. Influence of Crust Layering and Thickness on Coseismic Effects of Wenchuan Earthquake[J]. Journal of Geodesy and Geodynamics, 2010, 30(4): 29-35 DOI:10.3969/j.issn.1671-5942.2010.04.006)
(  0) 0) |
| [16] |
徐彦, 邵文丽. 2013年4月20日四川芦山7.0级地震震源破裂特征[J]. 地球物理学报, 2013, 56(10): 3 396-3 403 (Xu Yan, Shao Wenli. Rupture Details of the 20 April 2013 Lushan M7.0 Earthquake[J]. Chinese Journal of Geophysics, 2013, 56(10): 3 396-3 403)
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China
 2024, Vol. 44
2024, Vol. 44


