在数据采集及处理领域,时间是影响分析结果的重要因素。在地震行业,数据采集器可分为地震数据采集器和地球物理观测设备数据采集器,由于观测频带与应用场景不同,对2种数采时间精度的要求差异很大。地震数据采集器主要用来采集地震发生时的振动信号,用于地震波的反演及震源破裂研究,对时间精度要求较高,目前国内外普遍采用GNSS授时的方式。而地球物理观测主要是针对长周期慢变物理量的静态观测,持续时间(或周期)较长,目前采用NTP授时较多,GNSS授时较少。
通常采用2个技术指标来评价数据采集设备的时间精度:授时精度和守时精度[1]。美国SANDIA国家实验室(SNL)通过地震数据采集器采集参考时钟源设备输出的分脉冲(pulse per minute,PPM)或时脉冲(pulse per hour,PPH)信号,分析检验地震数采的相对时钟精度[2-4]。国内对地震数据采集器技术参数和性能的测试已有成熟的行业规范[1],与国外测试方法相似,均采用高精度时间源作为标准源,输出标准分号脉冲或秒号脉冲给地震数据采集器的输入端。地震行业对地球物理观测设备数据采集器时间精度的要求不高(通常是24 h守时精度为1 s),误差精度测量主要通过与UTC时间进行人工比对的方式完成,由于人工目测只在s级,精度较低,结果并不严谨。本文提出一种针对低采样数据采集设备的时间精度测试方法,旨在提高地球物理观测设备数据采集器等低采样设备的时间精度。
1 测量原理与方法评价低采样数据采集设备时间精度的基本思想,是选取一个钟差τ0已知的高采样数据采集设备作比对,将低失真的正弦波信号同时同相加载到高采样数据采集设备和低采样数据采集设备输入端,截取同一时段相同时刻的数据,运用曲线拟合或快速傅里叶变换(FFT)等方法对采集的数据进行处理和运算,计算出各数据采集设备对应的初始相位φ,将2个初始相位间的相位差反映的时间差Δt减去高采样数据采集器已知的钟差τ0,即得到低采样数据采集设备的钟差。
设高采样数据采集器的量程为EH,采样率为fH,低采样数据采集器的量程为EL,采样率为fL。给二者同时加载一个低失真正弦波信号e(t),其中正弦波的幅度满足
| $ e(t)=E \sin \left(2 \pi f_0 t+\varphi_0\right)+d_0 $ | (1) |
式中,φ0为初始相位,d0为信号的直流偏置值。
由于实际的采集数据是一些离散值,因此时间也是离散化的,不同采样率对应的时间离散度不同。设低采样和高采样数据采集设备离散化的时间分别为ti和tj,而相同时段内采集的数据个数也不同,分别设为n和m。低采样数据采集器第i个测量点的时刻为:
| $ t_i=\Delta t_i i=\frac{i}{f_L}, i=1, 2, \cdots, n $ | (2) |
高采样数据采集器第j个测量点的时刻为:
| $ t_j=\Delta t_j j=\frac{j}{f_H}, j=1, 2, \cdots, m $ | (3) |
启动波形采集,获得低采样数据采集器采集的数据xLi(i=1,2,3,…,n)和高采样数据采集器的数据xHj(j=1,2,3,…,m)。低采样数据采集器的输出波形可表示为:
| $ \begin{gathered} a_L\left(t_i\right)=A_L \sin \left(2 \pi f_0 t_i+\varphi_L\right)+d_L= \\ A_L \sin \left(\omega_L i+\varphi_L\right)+d_L \end{gathered} $ | (4) |
式中,ωL=2πf0/fL,-π/2≤φL≤π/2。则φL对应的初始时刻为:
| $ t_{0 L}=\varphi_L / 2 \pi f_0 $ | (5) |
同理,高采样数据采集器的输出波形可表示为:
| $ \begin{gathered} a_H\left(t_j\right)=A_H \sin \left(2 \pi f_0 t_j+\varphi_H\right)+d_H= \\ A_H \sin \left(\omega_H j+\varphi_H\right)+d_H \end{gathered}z $ | (6) |
式中,ωH=2πf0/fH,-π/2≤φH≤π/2。则φH对应的初始时刻为:
| $ t_{0 H}=\varphi_H / 2 \pi f_0 $ | (7) |
通过分析可知,运用曲线拟合或FFT方法均可得到低采样和高采样对应的初始相位φL和φH,将二者对应的时间差减去高采样数据采集设备的钟差τ0,即为低采样数据采集器的授时精度,具体公式为:
| $ \tau_L=t_{0 L}-t_{0 H}-\tau_0=\frac{\varphi_L-\varphi_H}{2 \pi f_0}-\tau_0 $ | (8) |
为保证采集数据的有效性,防止低采样数据采集设备和高采样数据采集设备在采集数据时出现信号混叠和削顶的情况,对输入的标准信号的幅值及频率、高采样数据采集设备的时间精度及适应范围提出相关技术要求:1)标准正弦信号的频率应小于低采样频率的0.5倍,幅值取2种数采量程最小值的0.5倍,且其失真度优于0.01%[1],同时该标准信号应是时间连续的信号;2)高采样数据采集设备的选取应具有较高的授时精度和守时精度,以保证低采样数据采集设备的守时精度测量值;3)本文方法适用于输入与输出具有线性关系的低采样数据采集设备的时间精度测试。
低采样数据采集设备的时间精度获取流程包括4个确定单元、1个获取单元和1个筛选单元。其中,第1确定单元用于确定待测低采样数据采集设备的第1采样频率,应选取低采样数据采集设备最高的采样率作为第1采样率。第2确定单元用于基于低采样数据采集设备所采集数据的维度和第1采样频率,确定采样频率大于第1采样频率的高采样数据采集设备。获取单元用于获取低采样数据采集设备对标准正弦信号利用第1采样频率采集的第1采样数据及高采样数据采集设备对预设信号利用第2采样频率采集的第2采样数据,第2采样频率应大于第1采样率的10倍。采集数据维度的选取要以低采样数据采集器采集的数据可识别标准信号的频率为准,在此基础上,维度越高越好。筛选单元用于基于第1采样数据,在第2采样数据中筛选出第3采样数据。第3确定单元用于根据第1采样数据和第3采样数据,确定低采样数据采集设备和高采样数据采集设备的时间差值。第4确定单元用于将时间差值和高采样数据采集设备的授时误差之差确定为低采样数据采集设备的授时误差。
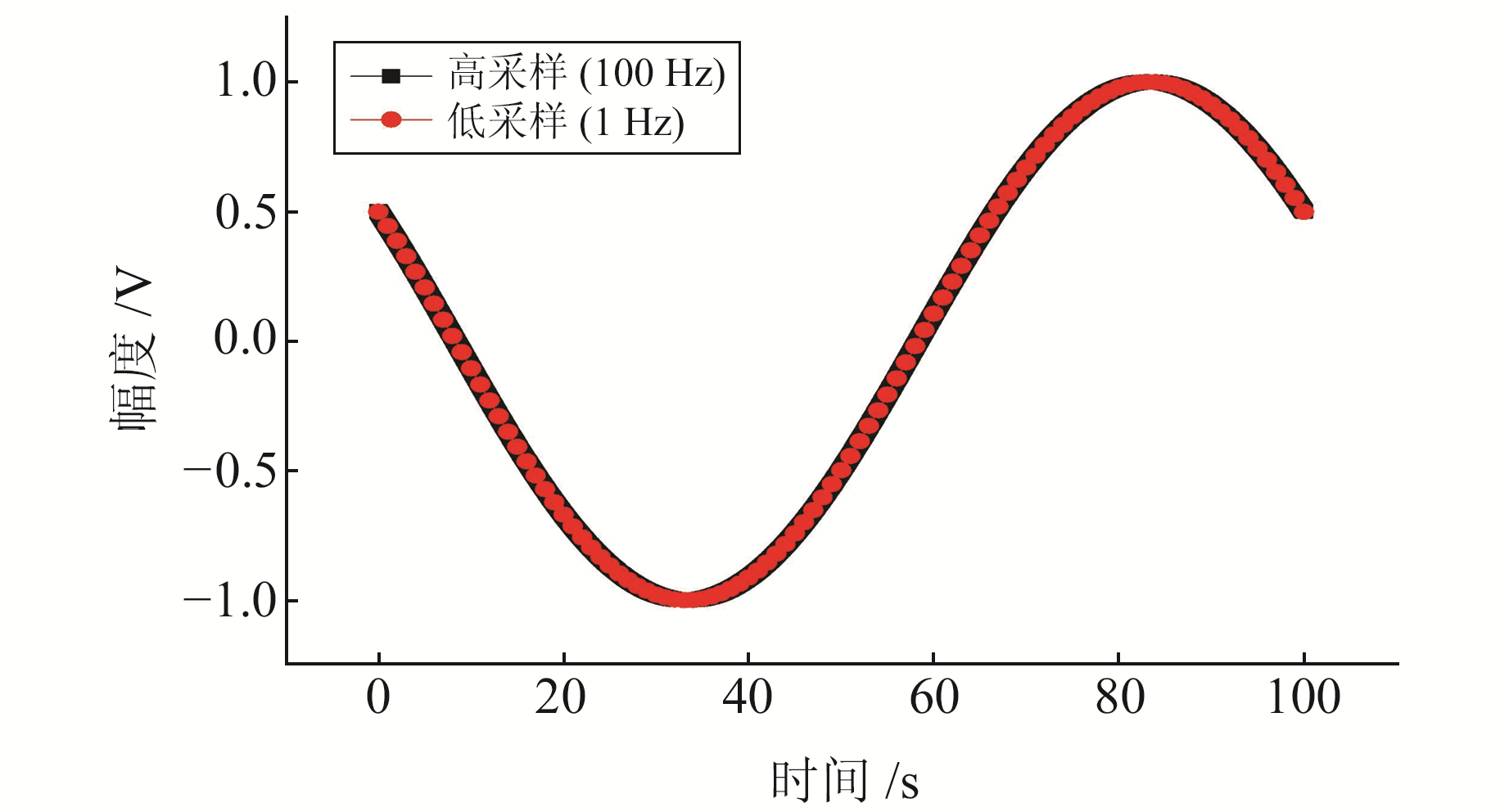
3 仿真验证与实例应用 3.1 仿真实验验证对本文时间精度测量方法进行仿真,取高采样率为100 Hz,低采样率为1 Hz;信号频率为0.01 Hz,幅度为1 V,初始相位为π/3,信号长度为10 000;设低采样比高采样采集时间超前10 ms。仿真波形如图 1所示。
|
图 1 仿真波形 Fig. 1 Simulation waveform |
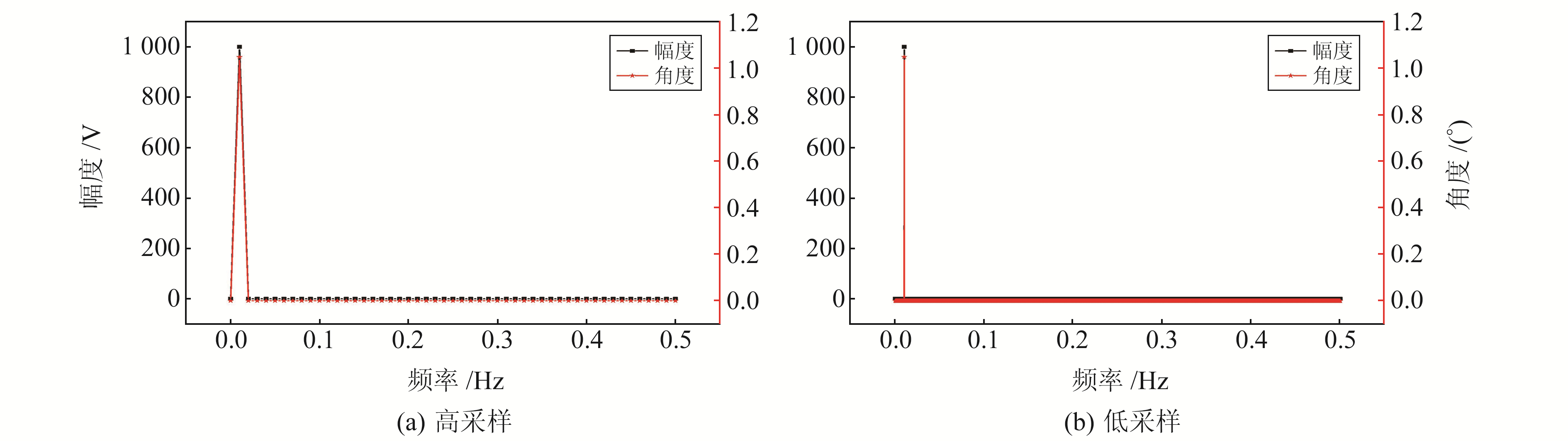
采用FFT方法对数据进行处理,获得2个采样频率下的初始相位,频率特性如图 2所示。图中截取的是0~0.5 Hz范围内的频率特性,由0.01 Hz对应相频特性来看,高采样的初始相位为1.047 2 rad,对应时间为16.676 3 s;低采样的初始相位为1.047 8 rad,对应时间为16.666 7 s, 2种采样率下的时间差为0.009 6 s(与0.01 s存在一定的误差,原因主要是FFT方法的数据处理精度不够高,也与信号长度有关),约为10 ms,验证了本文方法的有效性。
|
图 2 仿真实验频率特性 Fig. 2 Frequency characteristics of simulation experiments |
以地球物理观测设备中的形变数据采集器为例对本文方法进行时间精度的测试和处理,选取地震数据采集器作对比,以DS360作标准器输出标准的正弦信号,其失真度为0.001%。表 1为所用设备的设置参数。
|
|
表 1 参数设置 Tab. 1 Parameter settings |
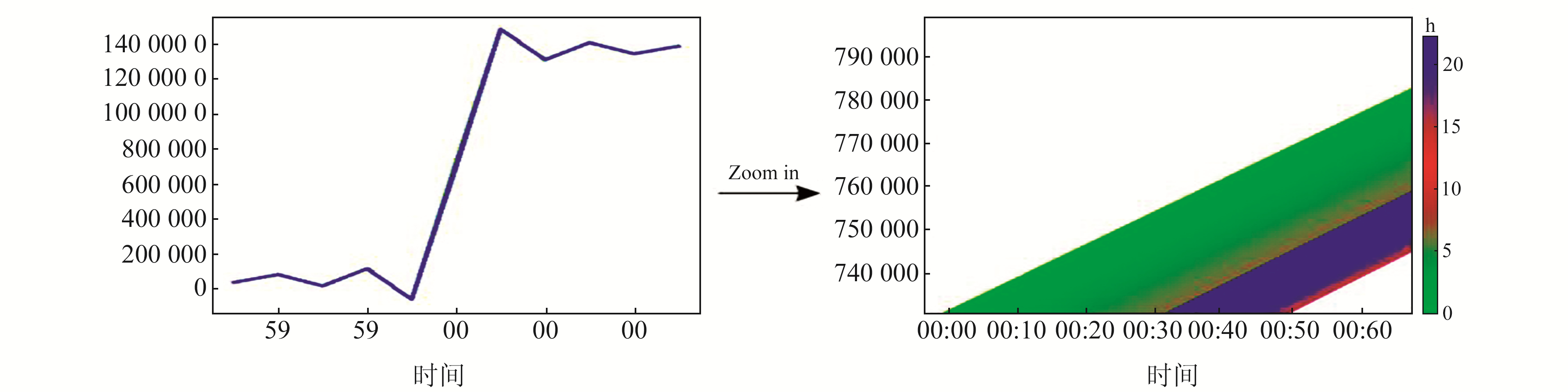
为查看所选参考设备是否符合测试要求,首先对地震数据采集器的授时精度进行测试。测试方法按照《地震观测仪器进网技术要求DB/T 22-2020地震仪》[1]中的方法,得到24 h的GPS授时精度误差如图 3所示。图 3绘制的是分脉冲信号的上升沿,包含1 440 min(24 h)的1 440条曲线,图 3(a)中看不出任何信号差。将上升沿不断放大后,从图 3(b)中可以清晰地看出,24 h的最大钟差为0.05 ms,即τ0为0.05 ms,授时离散度也很小,说明参考数采稳定性很好,满足形变数采24 h时间漂移测试的要求。
|
图 3 地震数据采集器24 h的GPS授时时间同步误差 Fig. 3 24 h GPS time synchronization error of seismic data collector |
对形变数据采集器进行NTP自动授时,待地震数据采集器授时稳定后,将DS360输出的正弦信号同时同向输入地震数据采集器和形变数据采集器输入端,并启动采集,下载相同时间同时段的数据。图 4为2个数采在相同时段20 min数据波形。

|
图 4 数采20 min数据波形 Fig. 4 Data acquisition for 20 min data waveform |
分别采用FFT方法和拟合法对数据进行处理,以获取2个数采的初始相位。形变数据采集器和地震数据采集器的采样率不同,将20 min数据长度作为FFT的信号长度,分别为1 200和120 000个点,因此二者频率特性的频率刻度不同。图 5为0~0.5 Hz范围内的频率特性,可以看出,形变数据采集器的初始相位为-1.199 2 rad,地震数据采集器的初始相位为-1.208 6 rad,通过式(8)计算得到形变数据采集器的钟差为149.75 ms。

|
图 5 实例频率特性 Fig. 5 Instance frequency characteristics |
应用正弦函数四参数拟合进行分析,拟合方法参考文献[5],具体计算结果为:形变数据采集器AL=990.89 mV,fL=0.012 Hz,φL=-1.194 2 rad,dL=-1.67 mV;地震数据采集器AH=993.94 mV,fH=0.012 Hz,φH=-1.204 4 rad,dH=-1.71 mV,通过式(8)计算得到形变数据采集器的钟差为162.33 ms。综合2种方法的计算结果可以看出,无论采用拟合法还是FFT方法,得到的形变数据采集器钟差均在ms级,可识别到μm级,满足地震行业对地球物理观测设备数据采集器时间精度的测试要求。
4 结语本文提出一种针对低采样数据采集设备时间精度的测试方法,首先选用时间精度稳定且授时误差已知的高采样数据采集设备作为参考设备,然后给测试数采和参考数采同时同相输入标准正弦信号,通过计算同时同段波形数据的初始相位差,得到测试的低采样数据采集设备的时间精度,实验验证本文方法具有有效性。通过本文方法可将低采样数据采集设备的时间测试精度提高至ms级甚至μs级,可用于输入与输出具有线性关系的地球物理观测设备数据采集器时间精度的测试。
| [1] |
中国地震局. 地震观测仪器进网技术要求: 地震仪DB/T 22-2020[S]. 北京: 地震出版社, 2020 (China Earthquake Administration. Technical Requirements of Instruments in Network for Earthquake Monitoring —Seismograph. DB/T 22-2020[S]. Beijing: Seismological Press, 2020)
(  0) 0) |
| [2] |
Kromer R P. Ground-Based Monitoring R and E Technology Report: Evaluation of the Kinemetrics/Quanterra Q330HR Remote Seismic System for IRIS/GSN[R]. Sandia National Laboratories, New Mexico, 2006
(  0) 0) |
| [3] |
Kromer R P. Ground-Based Monitoring R and E Technology Report: Evaluation of the Refraction Technology RT130HR Remote Seismic System for IRIS/GSN[R]. Sandia National Laboratories, New Mexico, 2006
(  0) 0) |
| [4] |
Merchant B J, Hart D M. Component Evaluation Testing and Analysis Algorithms[R]. Sandia National Laboratories, New Mexico, 2011
(  0) 0) |
| [5] |
梁志国. 通道间延迟时间差的测量不确定度[J]. 计量学报, 2005(4): 354-359 (Liang Zhiguo. The Measurement Uncertainty of Delay between Channels[J]. Acta Metrologica Sinica, 2005(4): 354-359)
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44

