在地电场观测中，工频干扰(50 Hz)是一种普遍存在的电磁干扰信号，会对正常观测产生严重影响。工频干扰主要由电力系统产生，分为感应电流和漏电电流2种，其中感应电流产生于交流输电线路，包括架空的超高压交流(35 kV以上)输电线路及电气化铁路的电力馈线(高架接触网或供电轨道)等；漏电电流则存在于各类用电设施附近，主要由于三相用电的不平衡，使接地系统产生强度不等的漏电电流^[1]。

为避免工频干扰对地电场观测产生影响，本文首先分析工频干扰的形成机理，探讨共模干扰和串模干扰的抑制方法及存在的缺陷，在此基础上提出利用过采样技术与两级数字滤波的工频串模抑制方法和利用两级浮地方式的工频共模干扰抑制方法，并应用于DCY-Ⅰ型地电场仪器的设计中，有效抑制了工频干扰。

1 地电场观测

我国地电场观测的对象主要为地电场水平分量，通过测量地表各测向之间的电位差获取大地电场、自然电场及其随时间的变化^[2-3]。地电场的观测装置大多采用三角型或十字型布极方式，将不极化电极分别部署在选定的观测场地内，通过外线设施送入观测室内，分别连接到地电场仪器的不同输入通道。根据《地震地电观测方法地电场观测DB/T 34-2009》^[3]的要求，地电场的观测频率范围为DC~0.1 Hz，采样率不大于1次/min，分辨率不大于0.5 mV/km，自然电场的分辨率不大于0.1 mV，因此地电场仪器的电压分辨率和噪声设计应不大于10 μV。

2 工频干扰及其影响 2.1 干扰形式

根据耦合方式，工频干扰可分为共模干扰和串模干扰。在地电场观测中，由于漏电电流等的影响，观测场地与观测仪器地之间会引入一定程度的电位差，从而形成共模干扰；而串模干扰的干扰信号则直接串联(叠加)在被测信号中，主要来自于2个测量电极，但干扰源基本集中在1个电极附近^[4]。

2.2 工频共模干扰对观测的影响

共模干扰对观测的影响可分为以下几种情况：

1) 输入线路完全对称的单端输入。双测量线的其中之一与仪器共地，共模干扰与观测仪器形成2个干扰回路，使仪器的信号地带有电压，最大可达几百V，导致仪器工作不正常甚至损坏。

2) 输入线路完全对称的差分输入。共模电压完全施加在差分输入的两端，与仪器地之间形成干扰电压，根据环境及距离等因素的不同，一般可达几V甚至上百V不等^[1]，很容易损坏观测仪器的元器件。

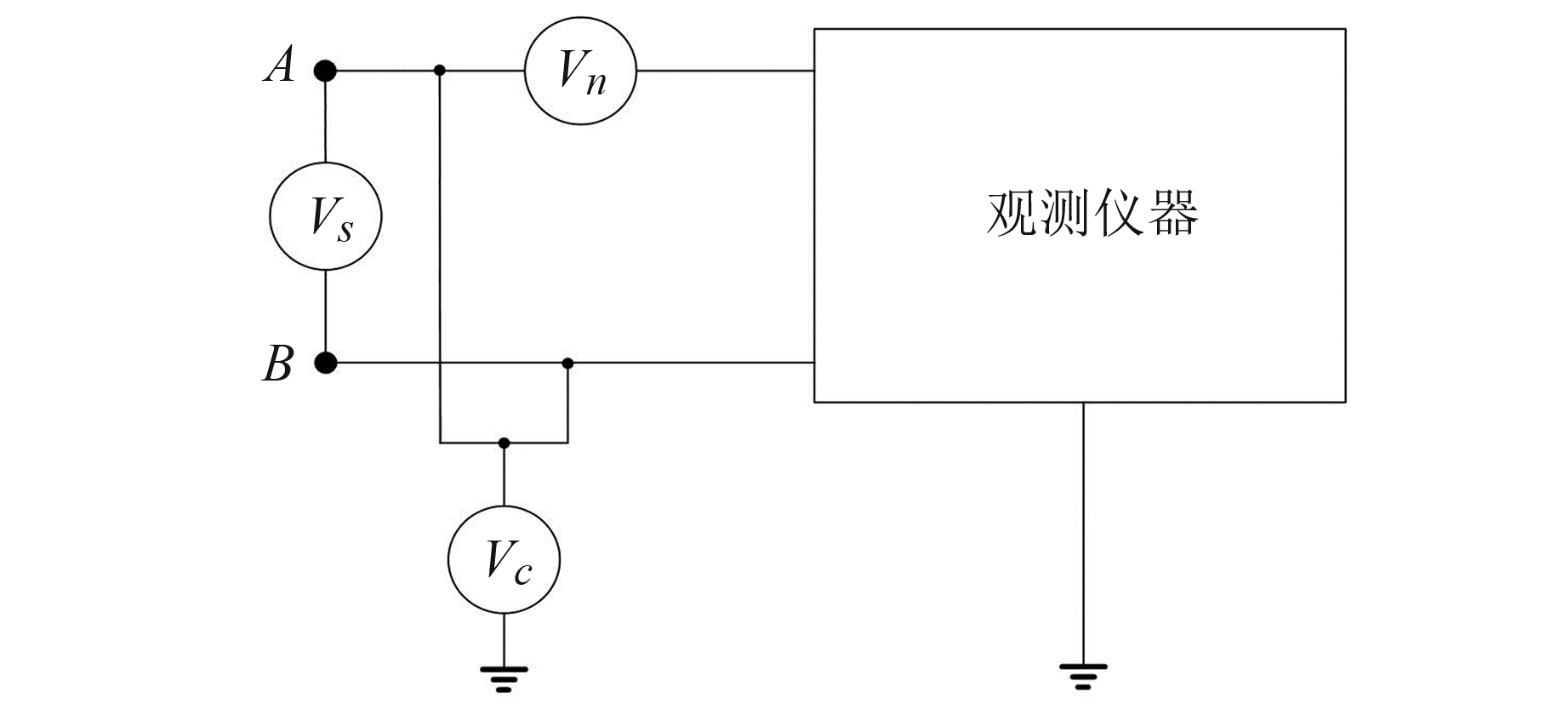
3) 输入线路不完全对称(图 1，图中V_s为被测信号，V_n为串模干扰信号，V_c为共模干扰信号)。作用于电极A的干扰为V_AN=V_n+V_c，作用于电极B的干扰为V_BN=V_c，因两输入端线路不完全对称，导致共模干扰信号转换为差模干扰，出现共模干扰与串模干扰共存的情况。

在地电场观测过程中，由于电极直接接地，通常采用差分输入的采集方式，同时两差分输入线路不能保证完全的对称，因此共模干扰对地电场观测的影响主要表现为第3种情况，即共模干扰与串模干扰共存。

2.3 工频串模干扰对观测的影响

工频串模干扰直接影响观测信号的大小，在采样率不高的情况下，干扰带来的危害主要包括限幅与频谱混叠。限幅是指由于工频干扰叠加在观测信号上，导致混合信号的大小超出观测仪器的正常输入动态范围，出现信号波形被削顶的现象，导致输出信号的幅度失真。根据采样定理^[5]，若从采样信号x(nT_s)中恢复原始信号，必须满足2个条件：1)x(t)为带限信号，其频谱X(ω)在|ω|＞ω_c的各处均为零；2)采样频率f_s不能过低，必须满足f_s≥2f_c，否则就会发生频谱混叠。理想采样及频谱如图 2所示。

图 2中，x(t)为输入带限信号，X(ω)为x(t)的频谱，A为x(t)的信号幅度，δ_Ts(t)为周期为T_s的单位冲激串，x(nT_s)为x(t)的采样结果，即

$ \begin{gathered} x\left(n T_s\right)=x(t) \delta_{T_s}(t)= \\ \sum\limits_{n=-\infty}^{\infty} x(t) \delta\left(t-n T_s\right) \end{gathered} $

(1)

由图 2可以看出，当$f_c<\frac{f_s}{2}$时，可利用x(nT_s)通过低通的方式恢复输入信号x(t)，反之则会出现频谱混叠。由于地电场观测的数据吐出率(1次/min)较低，当观测信号中存在工频串模干扰信号时，频谱混叠效应可能会产生类似直流或低频扰动性干扰^[1]。

3 工频干扰常用处理方法 3.1 工频共模干扰抑制方法

地电场观测的工频共模干扰来源于观测场地与观测仪器地之间存在的电位差，抑制共模干扰常用的方法有共模电感、共模电容、双绞线抗干扰、差分输入及浮地等方式^[6]。各干扰抑制方法的工作原理如下：

1) 共模电感是利用共模电流通过共模电感时，磁环中互相叠加的磁通对共模电流起到抑制作用。

2) 共模电容是利用电容通交流阻直流的特性，将特定频率的交流信号旁路到地，实际应用中多采用LC或RC方式通过调节谐振频率点实现陷波。

3) 双绞线抗干扰通过保证两测量线完全对称，使两测量线终端负载的总干扰电流相互抵消，以抗共模干扰。

4) 差分输入是利用两测量线上电压相减的方式去除共模干扰。

5) 浮地方式通过断开共模干扰的回路通道，形成无穷大的阻抗，使共模电流极其微小，从而起到抑制工频共模干扰的目的^[4]。

3.2 工频串模干扰抑制方法

工频串模干扰的抑制方法除了差模电感及差模电容外，还包括模拟滤波器、积分方法、模数转换器陷波器及数字滤波器等，其中差(共)模电感、电容因体积较大，常被应用于抑制高频干扰。

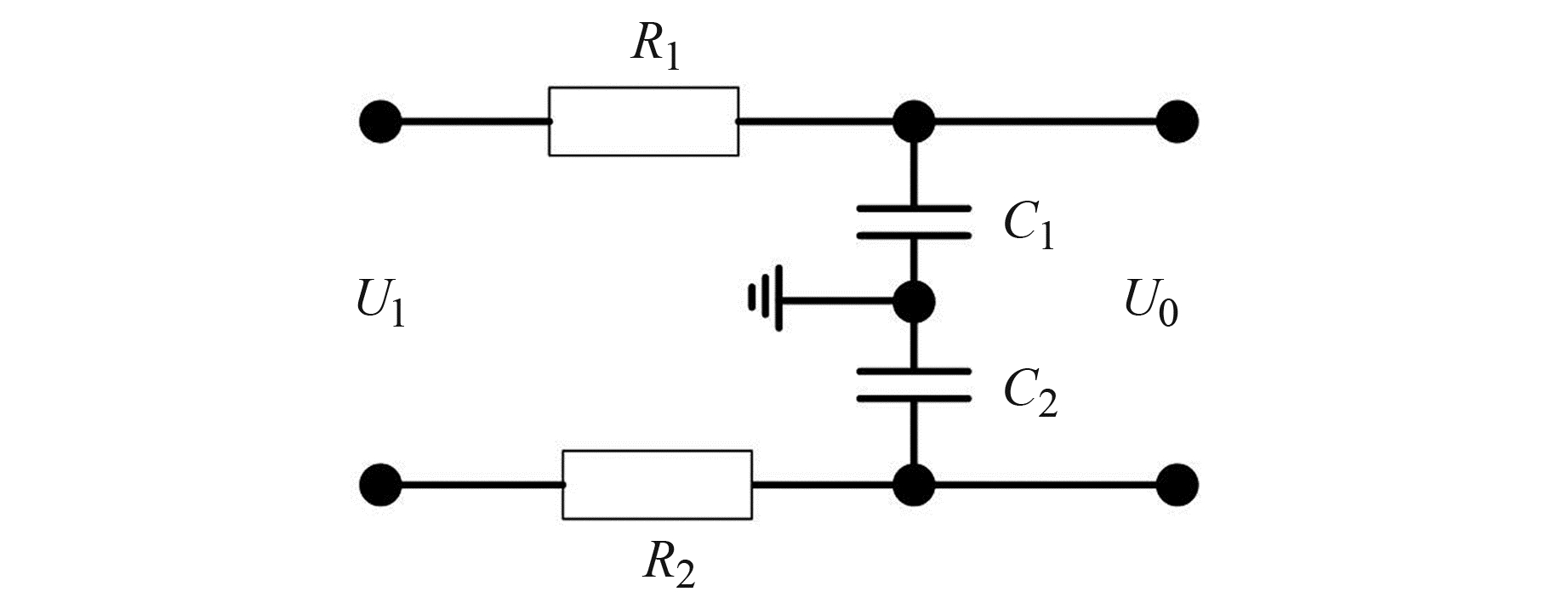
3.2.1 模拟滤波器

工频抑制的模拟滤波器通常包括低通滤波器与陷波器2种，位于模拟信号的处理电路部分。RC无源滤波器是信号处理过程中最常用的一种低通滤波手段，通过在2个信号测量输入端设计对称的RC滤波电路，以降低输入信号的带宽，如图 3所示。

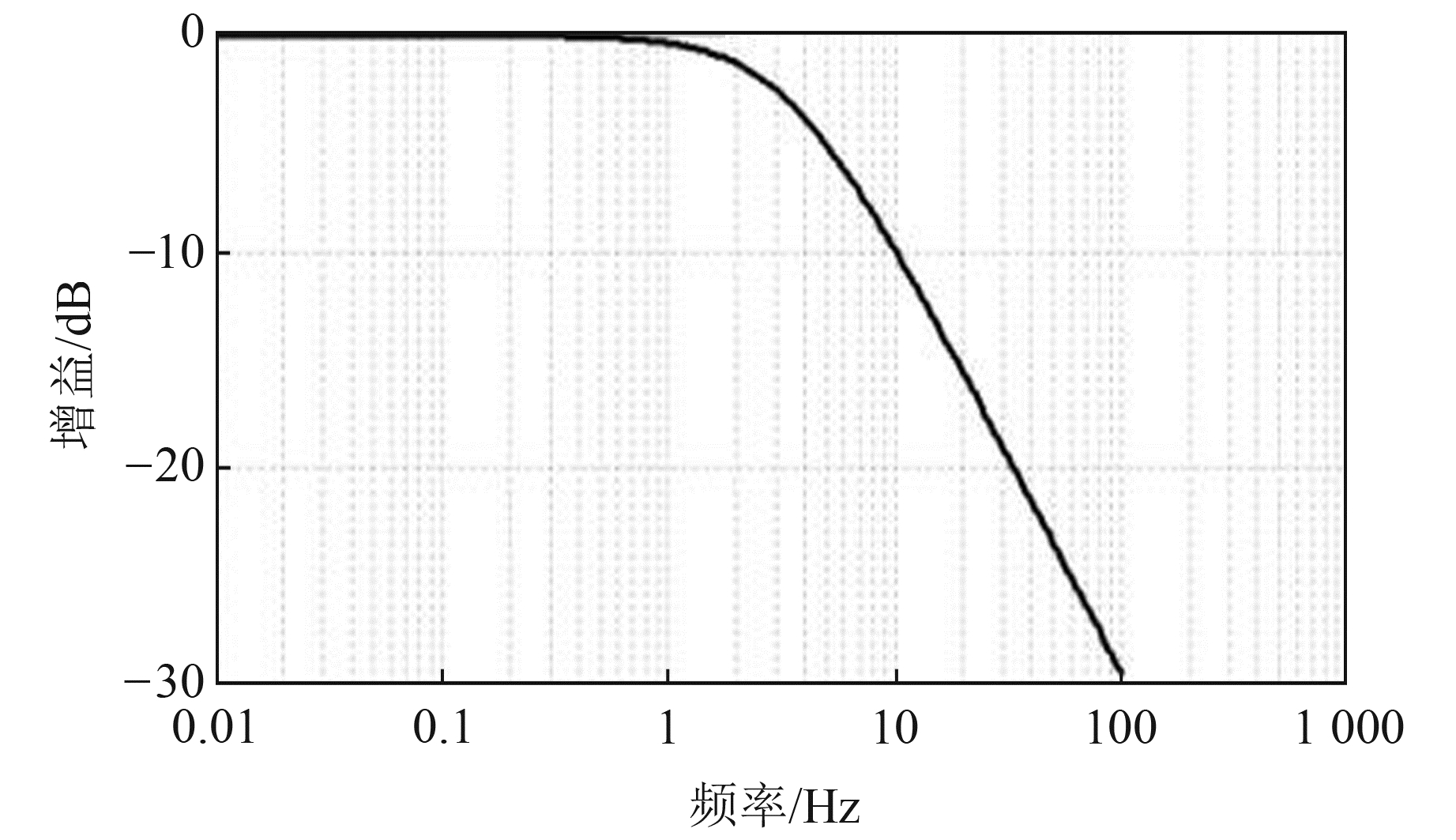
图 3中，R₁=R₂，C₁=C₂，R₁C₁与R₂C₂越大滤波效果越好，但也不能太大，否则会降低系统的响应速度。该RC滤波电路对工频干扰的抑制能力可达30 dB^[4]，即当等效的单端一阶RC低通滤波器中R=10 kΩ、C=4.7 μF时，系统的幅频响应曲线如图 4所示。可以看出，当时间常数τ=0.047时，工频干扰的抑制能力大概在24 dB左右，假如工频干扰信号为500 mV，经一阶滤波器衰减后还有35.55 mV，欠采样后会对观测信号产生很大的干扰。

陷波器是某一小频率范围内的带阻滤波器，如常用的双T型陷波器，该陷波器由一组T型RC低通滤波器与一组T型RC高通滤波器组成，如图 5所示。

图 5中，输入电压为U_i，输出电压为U_o，m点电压为U_m，n点电压为U_n。根据基尔霍夫电流定律，分别得到节点m、节点n与节点k的KCL方程为：

$ \frac{\left(U_i-U_m\right)}{R}=\frac{\left(U_m-U_o\right)}{R}+U_m \cdot s C $

(2)

$ \left(U_i-U_n\right)s C=2 \frac{U_n}{R}+\left(U_n-U_o\right){s C} $

(3)

$ \frac{\left(U_m-U_o\right)}{R}=-\left(U_n-U_o\right){s C} $

(4)

联立式(2)~式(4)，最终得到陷波器的传递函数H(s)为：

$ H(s)=\frac{U_o}{U_i}=\frac{1+(s R C)^2}{1+4 s R C+(s R C)^2} $

(5)

令$s=\mathrm{j} \omega, \omega_0=\frac{1}{R C}$，则有：

$ H(\mathrm{j} \omega)=\frac{1-\left(\frac{\omega}{\omega_0}\right)^2}{1-\left(\frac{\omega}{\omega_0}\right)^2+4\left(\frac{\mathrm{j} \omega}{\omega_0}\right)} $

(6)

当$f_0=\frac{1}{2 \pi R C}=50 \mathrm{~Hz}$时，$R C=\frac{1}{314}$，令C=0.1 μF，则R=31.85 kΩ，传递函数的幅频曲线如图 6所示。由图可见，陷波器对工频抑制的能力较一阶RC低通滤波器有很大提升，理论上可达75 dB左右。虽然阻带越窄陷波效果越好，但电路不稳定会引起振荡，常见衰减为40~50 dB。对于500 mV的工频干扰，经过陷波器滤波后仍有1.6 mV左右，比常规地电场观测信号小0~1个数量级。

3.2.2 积分方法

通过在时间T内对测试信号进行积分，测量其平均值，当积分时间T取为干扰周期(T₁)的整倍数时，即T=nT₁，则在积分的线性范围内，干扰信号的积分平均值为零。该方法理论上对固定频率(工频50 Hz及其谐波)有无限大的抑制能力^[4]，双积分型模数转换器就是基于该原理的。双积分型模数转换器ADC通过利用正反2次积分，将输入的模拟电压信号转换成与之成正比的时间宽度，然后在该时间宽度内对固定频率的时钟脉冲进行计数，计数结果即为正比于输入模拟电压的数字信号。工作原理如图 7所示。

首先，固定T₁对输入信号进行正向积分，T₁的长度通过周期脉冲计数为N₁，不同大小的输入信号其平均值对应不同斜率的积分，如图 7中V_o1与V_o2；然后对－V_ref(参考电压)进行反向积分，由于电压固定，故斜率固定，当2次积分结果为零时，反向积分所用时间脉冲计数为N₂，最终得到$\bar{V}_i=\frac{N_2}{N_1} \times V_{\mathrm{ref}}$。理论上，通过设计积分时间T₁=$n \times\left(\frac{1}{50}\right)$ (n为正整数)可很好地实现抑制固定工频(50 Hz)的目的，但实际应用中由于干扰信号不稳定，该方法目前对工频抑制的能力仅为40 dB左右，即500 mV的工频干扰经积分后仍有5 mV，与常规地电场观测信号的量级基本相当，仍不能满足地电场观测的要求。

3.2.3 模数转换器陷波器

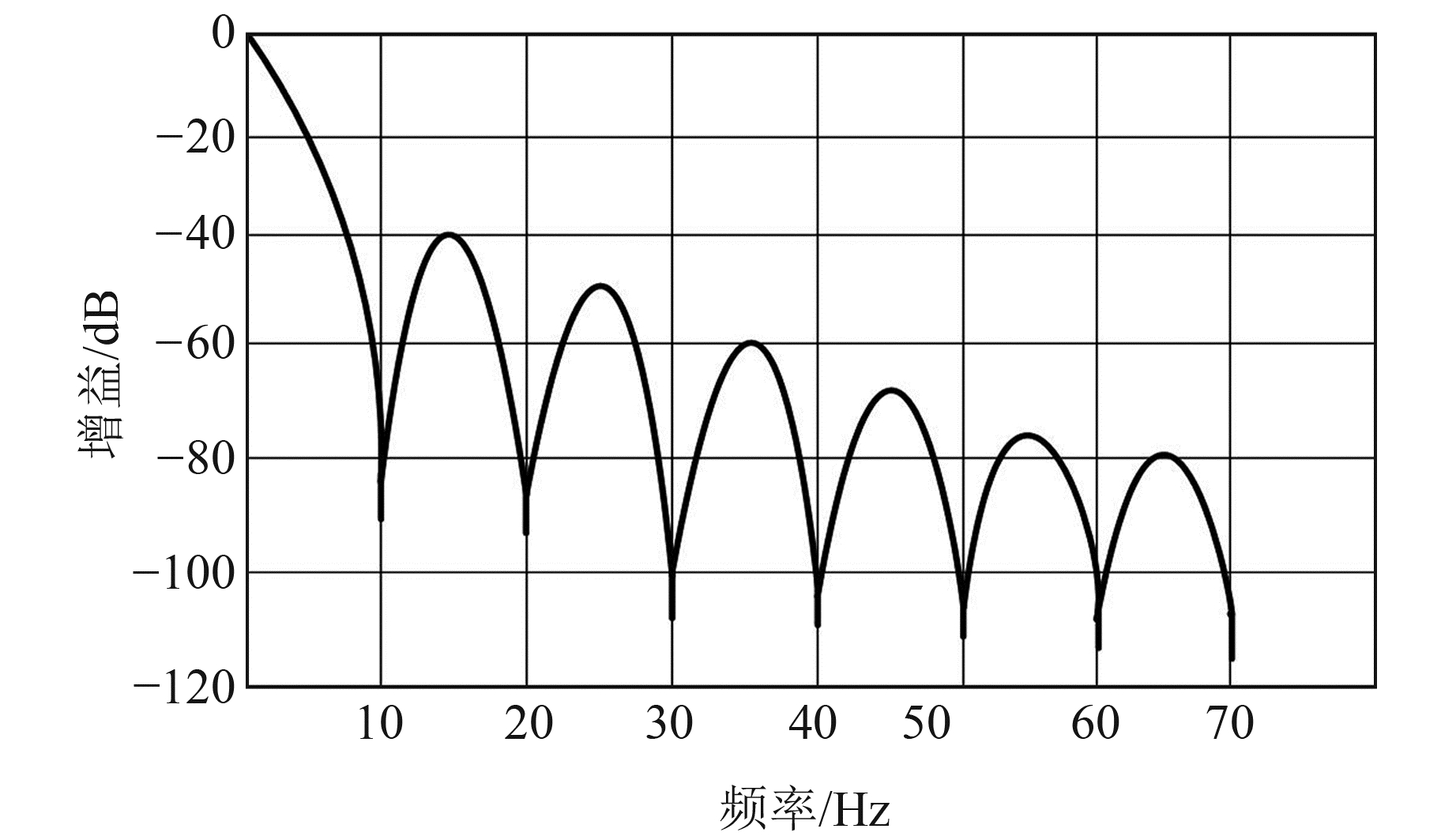
在模数转换阶段，利用模数转换器(ADC)自身提供的陷波器也可实现对工频50 Hz的抑制。常用的高分辨率Σ-ΔADC通常内部都集成SINC滤波器与FIR滤波器，地电场信号属于近直流信号，通过设置其SINC滤波器，利用梳状滤波的各个陷波点，可抑制工频与倍频干扰信号。如AD7710内部集成具备$\left(\frac{\sin x}{x}\right)^3$响应的数字滤波器，通过设置采样频率可改变梳状滤波器的陷波频率点，数据吐出率越低，ADC的有效分辨力越高^[7]。图 8为AD7710在数据吐出率为10 Hz时的SINC3频响曲线，可以看出，其对工频50 Hz的抑制能力理论上可达100 dB，即对于500 mV工频干扰，经SINC滤波后为0.005 mV，比常规地电场观测信号小3~4个数量级。相比而言，该方法对工频串模的抑制能力较好。

3.2.4 数字滤波器

数字滤波器是由数字乘法器、加法器和延时单元组成的一种算法或装置，由具有递推关系的差分方程表示。根据单位冲激响应的不同又分为IIR(无限脉冲响应)与FIR(有限脉冲响应)滤波器，其中IIR滤波器基于有理分式表示的系统函数逼近所需的频率响应，单位冲激响应是无限的，计算量小，但不能实现严格的线性相位。而FIR滤波器基于有理多项式表示的系统函数逼近所需的频率响应，单位冲激响应有限，可实现严格的线性相位，但计算量很大，对于低速处理器来说，很难利用软件的方式实现效果理想的FIR滤波器。其差分方程与传递函数为。

$ y(n)=\sum\limits_{i=0}^{N-1} b_i x(n-i) $

(7)

$ H(z)=\sum\limits_{i=0}^{N-1} b_i z^{-i} $

(8)

若设计可抑制工频干扰的滤波器，根据零、极点相消原理，可先设计一个FIR梳状滤波器，该滤波器的陷波点包含工频及谐波点，然后利用极点抵消零点处的零点^[5]，最终得到具有IIR结构的FIR低通滤波器。该滤波器的输入输出之间具备简单系数关系，可通过计算起到抑制工频干扰的目的。

首先，在Z平面单位圆上均匀设置由M个零点构成的FIR梳状滤波器，得到H(z)的分子为1－z^－M，再利用零、极点相消的原理在z=1处设置一个极点，抵消该处的零点^[5]，得到H(z)的分母为1－z^－1，则系统的传递函数为：

$ H(z)=\frac{1-z^{-M}}{1-z^{-1}} $

(9)

频响应特性H(e^jw)为：

$ H\left(\mathrm{e}^{\mathrm{j} \omega}\right)=\mathrm{e}^{-\mathrm{j} \omega \frac{(M-1)}{2}} \times \frac{\sin \left(\omega \frac{M}{2}\right)}{\sin \left(\frac{\omega}{2}\right)} $

(10)

为更好地起到50 Hz谐波陷波作用，采样率f_s设为工频频率的整数倍，设f_s=250 Hz，取M=250，即|z|=1的单位圆等分为250份，各等分点均设置零点，故梳状滤波器的零点为z_k=$\mathrm{e}^{\mathrm{j} \frac{2 \pi}{M} k}(k=0, 1, 2 \cdots, M-1)$，带宽为1 Hz，在z=1处设置极点抵消零点z_k|_k=0，得到具有线性相位的系统响应函数为：

$ H\left(\mathrm{e}^{\mathrm{j} \omega}\right)=\mathrm{e}^{-\mathrm{j} \omega \frac{249}{2}} \times \frac{\sin \left(\omega \frac{250}{2}\right)}{\sin \left(\frac{\omega}{2}\right)} $

(11)

幅频响应曲线如图 9所示，可以看出，当ω=0时取最大值|H(e^jω)|_ω=0=250。为使该点处幅值为1，则系统函数需衰减1/250，即

$ H\left(\mathrm{e}^{\mathrm{j} \omega}\right)=\mathrm{e}^{-\mathrm{j} \omega \frac{249}{2}} \times \frac{1}{250} \times \frac{\sin \left(\omega \frac{250}{2}\right)}{\sin \left(\frac{\omega}{2}\right)} $

(12)

由此得到：

$ H(z)=\frac{1}{250} \times \frac{1-z^{-250}}{1-z^{-1}} $

(13)

故差分方程为：

$ \begin{gathered} y(n)=y(n-1)+ \\ \frac{1}{250}(x(n)-x(n-250)) \end{gathered} $

(14)

由式(14)可知，该差分方程的计算量很小，且系统在工频频点与倍频处均有一定的抑制作用。

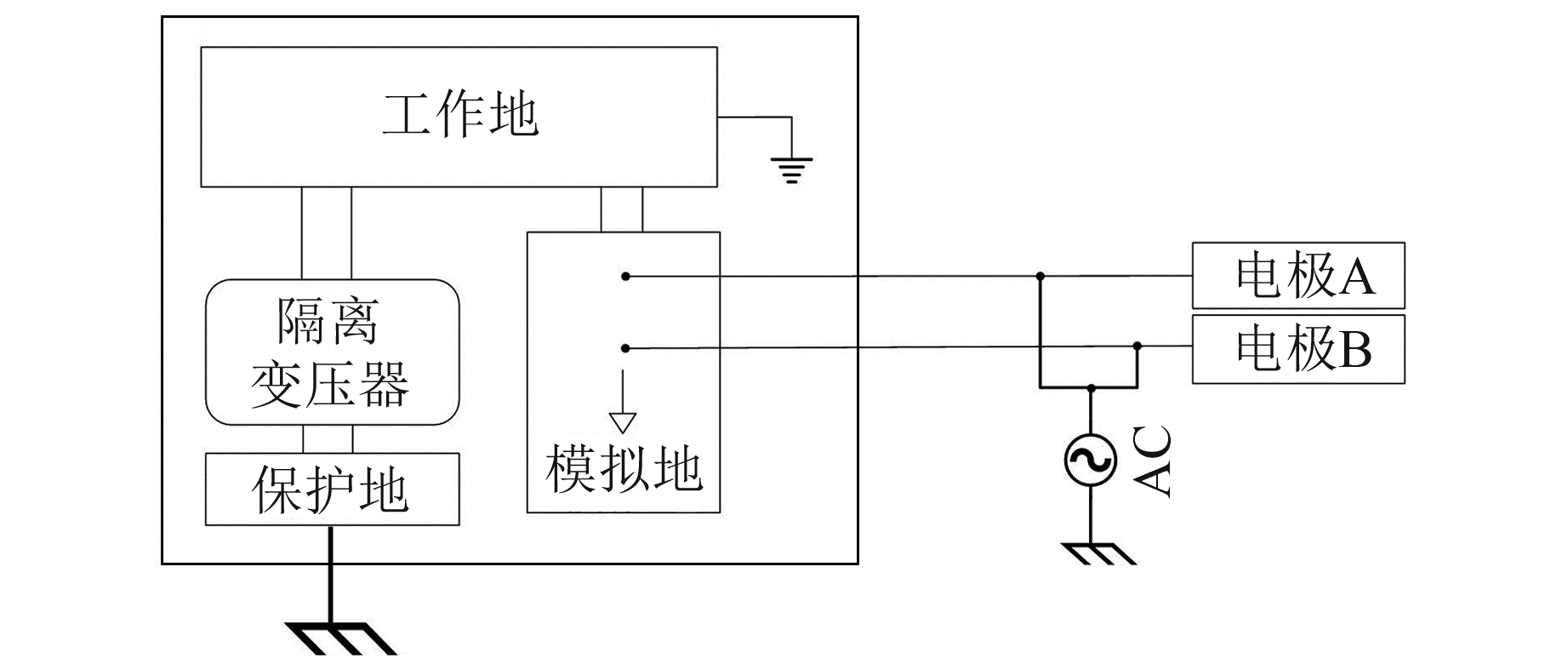
4 DCY-Ⅰ型电场仪工频干扰抑制方法 4.1 工频共模干扰抑制措施

DCY-Ⅰ型地电场仪采用两级浮地的设计方式抑制工频共模干扰。首先是AC/AC隔离，即利用隔离变压器为仪器提供交流供电，将仪器的工作地与保护地完全隔离，保护地接测量仪器外壳并与大地相通，工作地作为后续电路所需电源的回路^[4]；另外是DC/DC隔离，即在采集电路的设计部分采用DC/DC隔离电源模块，将模拟信号的供电回路与其他数字电路的供电回路相互隔离，将仪器的工作地与模拟信号处理电路地断开，如图 10所示。

通过两级浮地的设计方式，可使观测仪器的工频共模抑制能力达到140 dB以上，对220 V交流共模干扰衰减到22 μV以下，比地电场观测信号小3~4个数量级，同时不影响对地电场观测信号的测量。

4.2 工频串模干扰抑制措施

DCY-Ⅰ型地电场仪的工频串模抑制采用硬件数字滤波的方法。随着芯片集成化程度与计算能力的提高，复杂的数字滤波器算法也可通过FPGA或MPU来实现，DCY-Ⅰ型地电场仪即采用FPGA芯片，设计了2级数字滤波器，最终实现由250 Hz采样到1 Hz数据输出。为防止输出信号中存在频谱混叠的现象，模数转换ADC部分采用250 Hz采样，模拟信号处理电路部分3 dB带宽限制在125 Hz以内，通过过采样的方式将50 Hz工频信号完整地采集进来，然后通过数字滤波的方法将高频信号去掉，最终将频带控制在0.1 Hz以下。设计的第1级FIR滤波器通带范围为DC~1 Hz，截止频率为2 Hz，带内波动为0.1 dB，带外衰减140 dB，滤波器阶数为1 288，经重采样后数据吐出率为10 Hz；第2级滤波器通带范围DC~0.05 Hz，截止频率为0.3 Hz，带内衰减0.1 dB，带外衰减140 dB，滤波器阶数为206，3 dB带宽在0.1 Hz，经重采样后数据吐出率为1 Hz。FIR滤波器的幅频响应曲线如图 11所示。通过2级FIR滤波的方式，可完全去除工频与高频干扰信号的影响，相比以前的工频抑制效果更加理想。

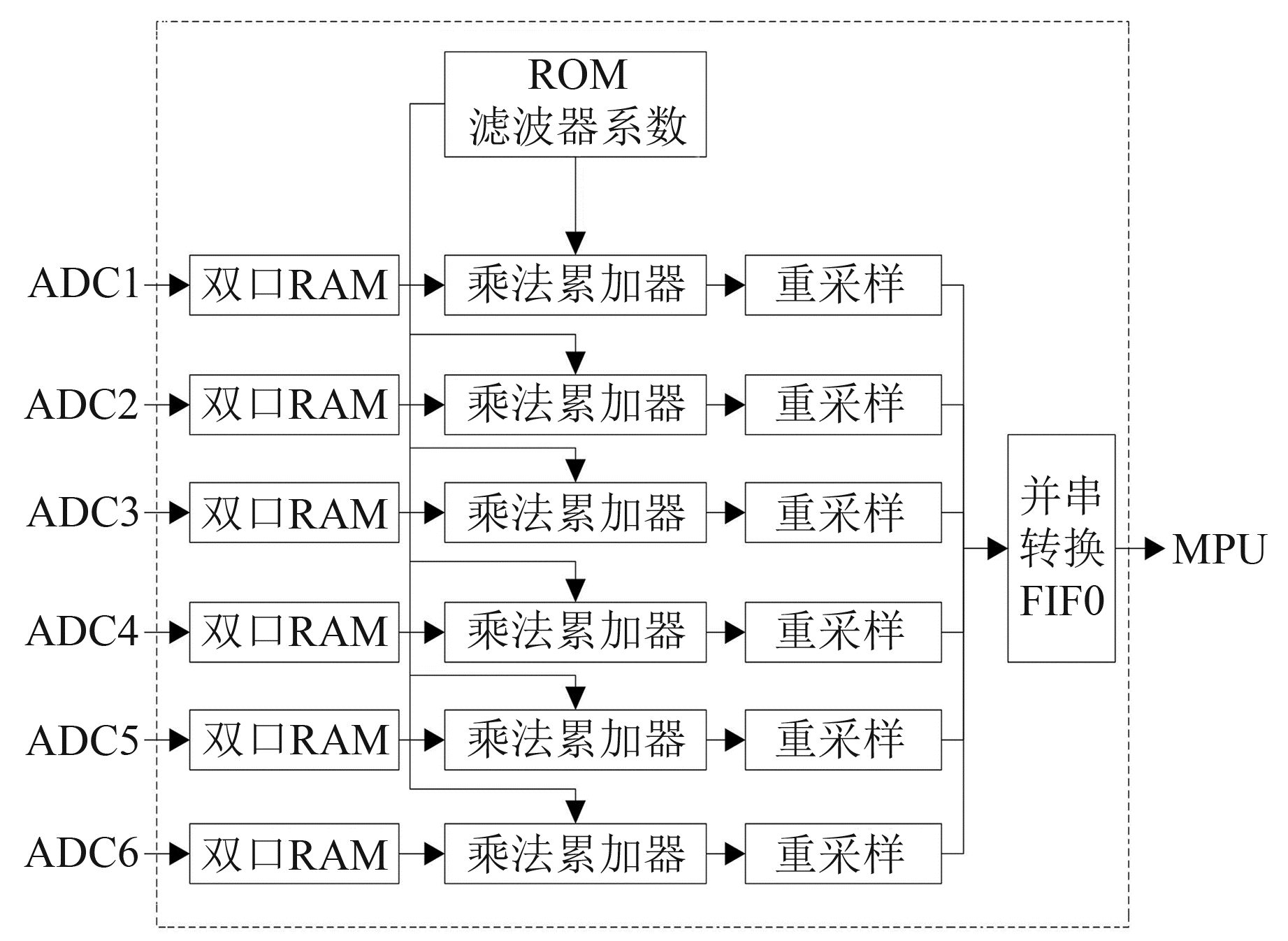
FIR滤波器的FPGA实现原理如图 12所示，图中来自测量装置的6路被测信号分别经ADC以250 Hz的采样率后，首先进入双口RAM单元进行数据缓冲，利用实例化的ROMIP核存放滤波器系数。根据直接型网络结构FIR的差分方程$y(n)=\sum\limits_{i=0}^{N-1} h(i) x(n-i)$读取ROM中的系数进行乘累加操作，得到的数据经截短后重采样，最终得到10 Hz的输出数据，再经通道开关依次送入并/串转换单元，以串行数据的方式提供给MPU。

DCY-Ⅰ型地电场仪采用的FPGA是由Altera公司生产的Cyclone Ⅲ系列芯片EP3C40F484，该芯片具备39 600个逻辑单元，1 134 Kbits RAM，内嵌乘法器126个，锁相环4个，IO端口300多个，经综合后占用逻辑单元6 413个，内存651 264 bits，乘法器72个，锁相环2个，IO端口95个。FPGA的工作时钟为50 MHz，比较容易实现6路采集信号的高阶并行数字滤波，经过第1级数字滤波器后完美地滤除了工频串模干扰信号。结果显示，工频串模抑制能力可达到80 dB(衰减4个数量级)以上，且无需担心发生频谱混叠。

4.3 应用效果

图 13为实验室环境下利用标准信号源提供的指定周期频率信号得到的仪器通频带曲线，可以看出，DCY-Ⅰ地电场仪对工频干扰的抑制能力已达到指标要求的80 dB以上。

在实验室环境，将标准信号源KEYSIGHT 33500B的输出分别加在500 Hz数采与DCY-Ⅰ地电场仪的信号输入端，通过设置不同的工频信号输出参数，测试2 d内仪器的工频抑制情况。表 1为工频(50 Hz)信号设置参数。

图 14为实验室环境下的工频干扰抑制测试曲线，其中曲线1为2023-06-27~28实验室环境下DCY-Ⅰ型地电场仪在不同工频信号输入情况下的秒数据输出曲线；曲线2为第2个工频参数调整时刻前后合计1 000点的500 Hz采样数据曲线；曲线3为第3个工频参数调整时刻前后合计1 000点的500 Hz采样数据曲线；曲线4为第4个工频参数调整时刻前后合计1 000点的500 Hz采样数据曲线。由图 14可以看出，实验室环境下DCY-Ⅰ型地电场仪对工频干扰的抑制效果显著。

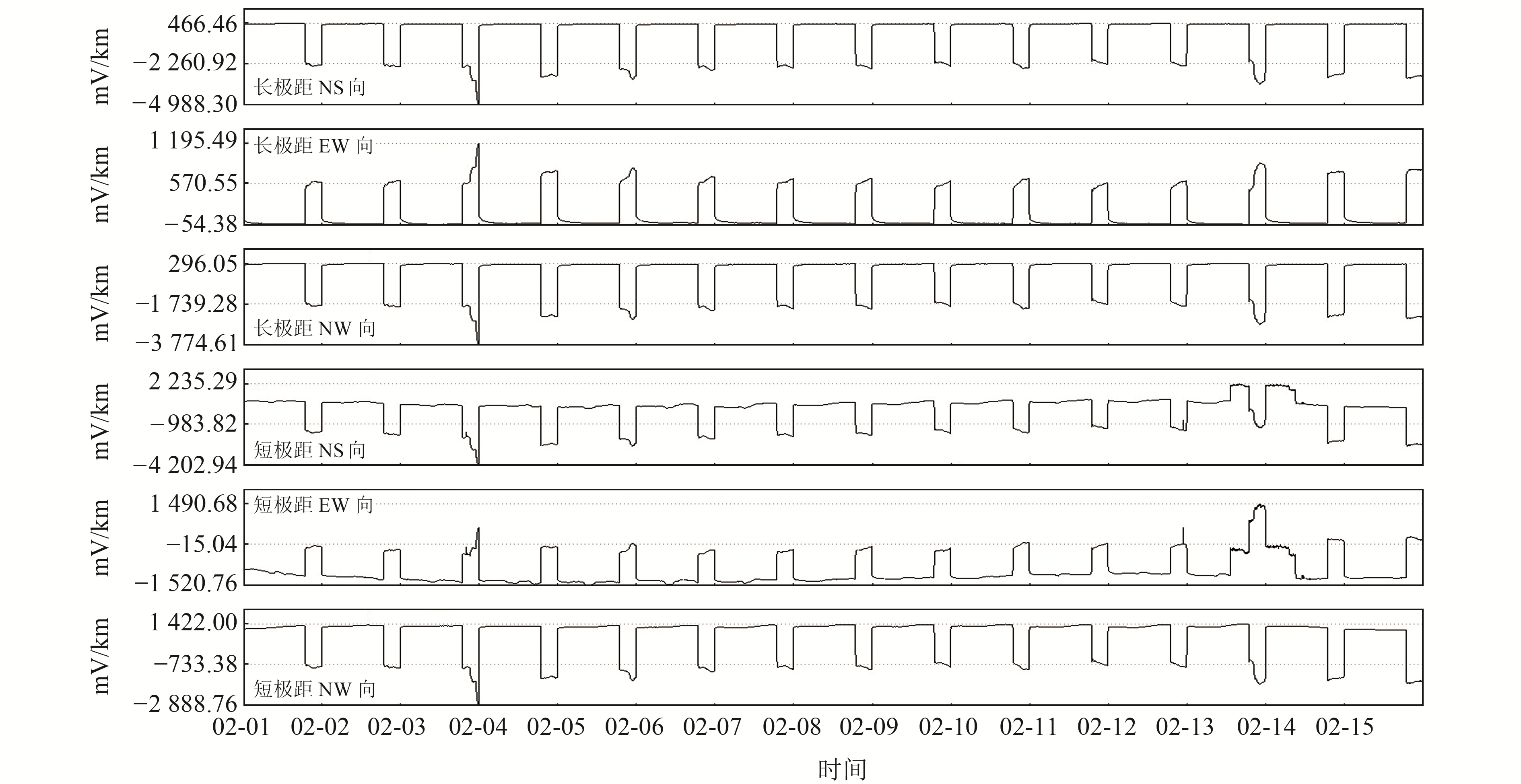
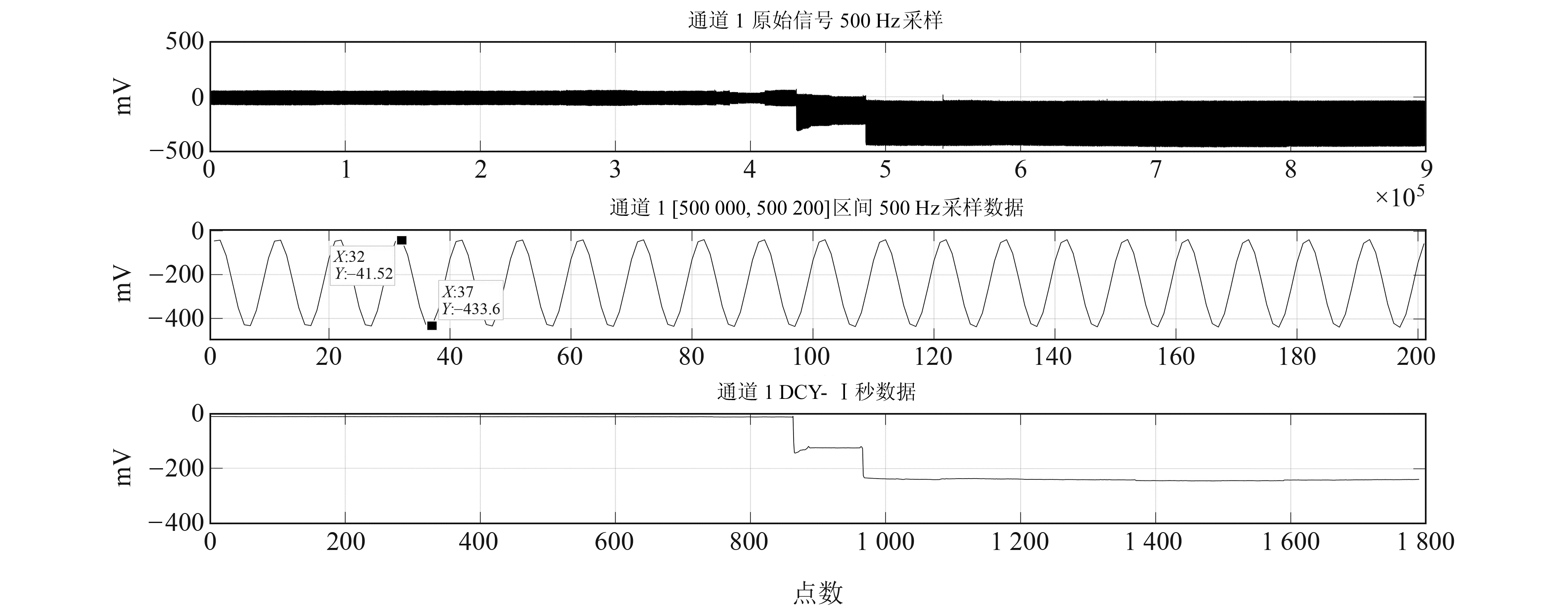
图 15~16为台站环境排查漏电干扰时的相关曲线。其中，图 15为海南琼中台2023-02-01~15地电场受干扰的原始观测数据曲线。可以看出，该观测点每天都会有一个固定时段有较大的漏电干扰，为排查干扰，同时架设DCY-Ⅰ型地电场仪与500 Hz采样的数采进行数据采集。图 16为交流漏电测试对比曲线，图中曲线1为0.5 h的500 Hz原始采样数据；曲线2为曲线1在500 000~500 200点区间展开时的曲线形状，其工频交流干扰成分V_pp约为385 mV；曲线3为DCY-Ⅰ地电场仪的秒数据曲线。可以看出，该漏电干扰中除直流漏电干扰外，还有工频干扰，并且工频交流50 Hz信号得到了很好的抑制，而直流漏电部分是无法消除的。

5 结语

地电场观测信号是通过电极直接获取的观测场地内的低频信号，因此信号中不可避免地会存在工频干扰。在技术条件和计算能力都受限的情况下，前人研制了很多工频抑制手段，包括共(串)模电感电容、模拟滤波器、积分方法、简单数字滤波器及双绞线与浮地等，取得了一定的效果，但仍不能满足地电场观测的需求。随着芯片集成度的提高，在保证时效的前提下，需要大量资源的高阶浮点数字滤波器得到实现，尤其是具有丰富资源及优异并行数据处理能力的FPGA芯片，特别适用于多通道数据处理。DCY-Ⅰ型地电场仪基于过采样方法，利用FPGA实现6通道高阶数字滤波器，既能很好地滤除工频串模干扰，又能避免频谱混叠的发生；同时采用两级浮地设计，确保工频共模干扰回路具有足够大的阻抗，起到抑制工频共模干扰的目的，在台站观测中取得了明显的效果。