2. 南方海洋科学与工程广东省实验室(珠海),广东省珠海市情侣北路,519000;
3. 甘肃省地震局,兰州市东岗西路450号,730000
目前国内正在运行的各类地倾斜观测仪器有300多套,主要有水平摆倾斜仪(SQ系列)、垂直摆倾斜仪(VS、VP)、水管倾斜仪(FSQ、DSQ)和井下摆倾斜仪(CZB)等[1-3],覆盖全国30个省、市、自治区及直辖市,积累了丰富的观测数据。通过对国家地震台网数据库的观测数据进行跟踪分析发现,部分测向的参数存在方位角不准确的问题。而根据技术规范要求,仪器定向方位角的测定精度应优于1°[4],若方位角未经测定或测定不准,都会影响观测资料的精度[5]。
为从整体上对各分量方位角的准确性快速给予定量评价,本文提出地倾斜视方位角及视偏角概念,并根据视偏角大小来区分起始方位角的准确程度。首先利用1 d内的24个时值数据(含理论值和观测值)作为实例,介绍视方位角的计算思路和方法;再基于有准确、稳定方位角及长观测序列的北京西拨子和兰州十里店水管倾斜仪5个测向分量数据,计算长序列视方位角,以大致了解水管倾斜视偏角的长序列动态特征;最后介绍2020年全国地倾斜台网715个测向分量的视偏角及离散误差的统计结果。根据结果,对于视偏角数字大于20°的测向分量的起始方位角应予以重点核查;对于视偏角离散误差MPS>20°的测向分量的观测数据应进行认真筛查。
1 视方位角的定义与计算 1.1 视方位角与NAKAI拟合结果地倾斜的观测对象是地平面与水平面之间(地平面法线与铅垂线)的夹角及其随时间的变化,具有大小和方向,单位为(″),要求观测精度为0.003″;视方位角的单位为(°),要求测定误差≤1°[1]。由日、月等天体引起刚性地球表面任意一点的地倾斜固体潮值称为地倾斜固体潮汐理论值,可以预先计算。在中纬度地区,地倾斜固体潮振幅可达3×10-2″左右,因此正常地倾斜观测都能记录到清晰、稳定的固体潮响应。由NAKAI公式[6-8]可知,地面某观测站在任意时刻t的地倾斜观测值与理论值之间的关系为:
| $ \begin{aligned} v_t & =a R_t+b R_t^{\prime}+\sum\limits_{l=0}^2 k_l t^l-Y_t \\ b & =a \cdot \mathrm{d} t \end{aligned} $ | (1) |
式中,a为观测振幅与理论振幅之比(振幅比),b为观测相位与理论相位之差(滞后因子),Yt为观测站A方向t时刻的观测值,Rt和R′t分别为观测站A方向t时刻的固体潮理论值及其变化率(理论值的一阶微商值)[2-4],
| $ \begin{aligned} & R_t=g_{\mathrm{NS}} \cos A+g_{\mathrm{EW}} \sin A \\ & R_t^{\prime}=g_{\mathrm{NS}}^{\prime} \cos A+g_{\mathrm{EW}}^{\prime} \sin A \end{aligned} $ | (2) |
显然a、b与方位角A有关。将真方位角A代入式(2)计算Rt和R′t,再代入式(1)便可得到a、b的准确结果。
1.2 视方位角的定义与计算将地倾斜观测数据与理论值进行NAKAI拟合,调整理论值的方位角,使其拟合状态达到最佳,此时的方位角即为地倾斜视方位角,以AS表示。为确定最佳拟合状态时的方位角AS,需得到最佳拟合状态时拟合参数a、b的基本特征。
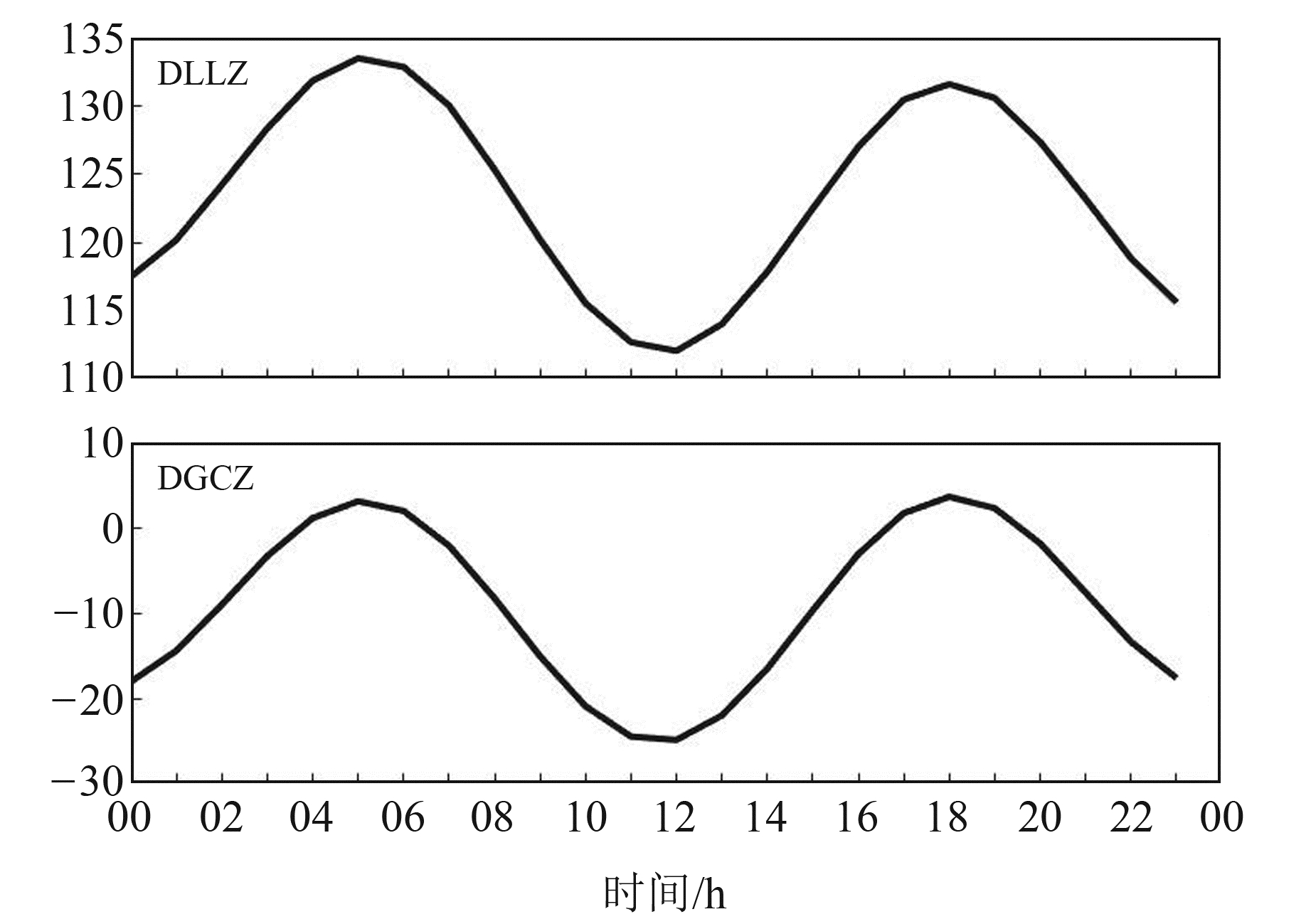
图 1为2018-01-01北京西拨子(λ=115.98°、φ=40.35°、H=640 m)地倾斜NS向(方位角A=0°)整点观测值和理论值的时序曲线,可以看出,二者相关性很好(单位:毫角秒)。
|
图 1 北京西拨子地倾斜理论值和观测值对比曲线 Fig. 1 Comparison curve between theoretical and observed values of ground tilt at Beijing Xibozi |
在0°~360°平面内,方位角A取不同值可得到不同的理论值,图 2为方位角A依次取15°、20°、45°和90°时的观测理论值(单位:毫角秒)。可以看出,随着方位角的增大,理论值曲线与观测值曲线的相位差愈发显著,观测值与理论值的NAKAI拟合状态越来越差。

|
图 2 北京西拨子理论值随方位角变化曲线 Fig. 2 The oretical value variation curve with azimuth at Beijing Xibozi |
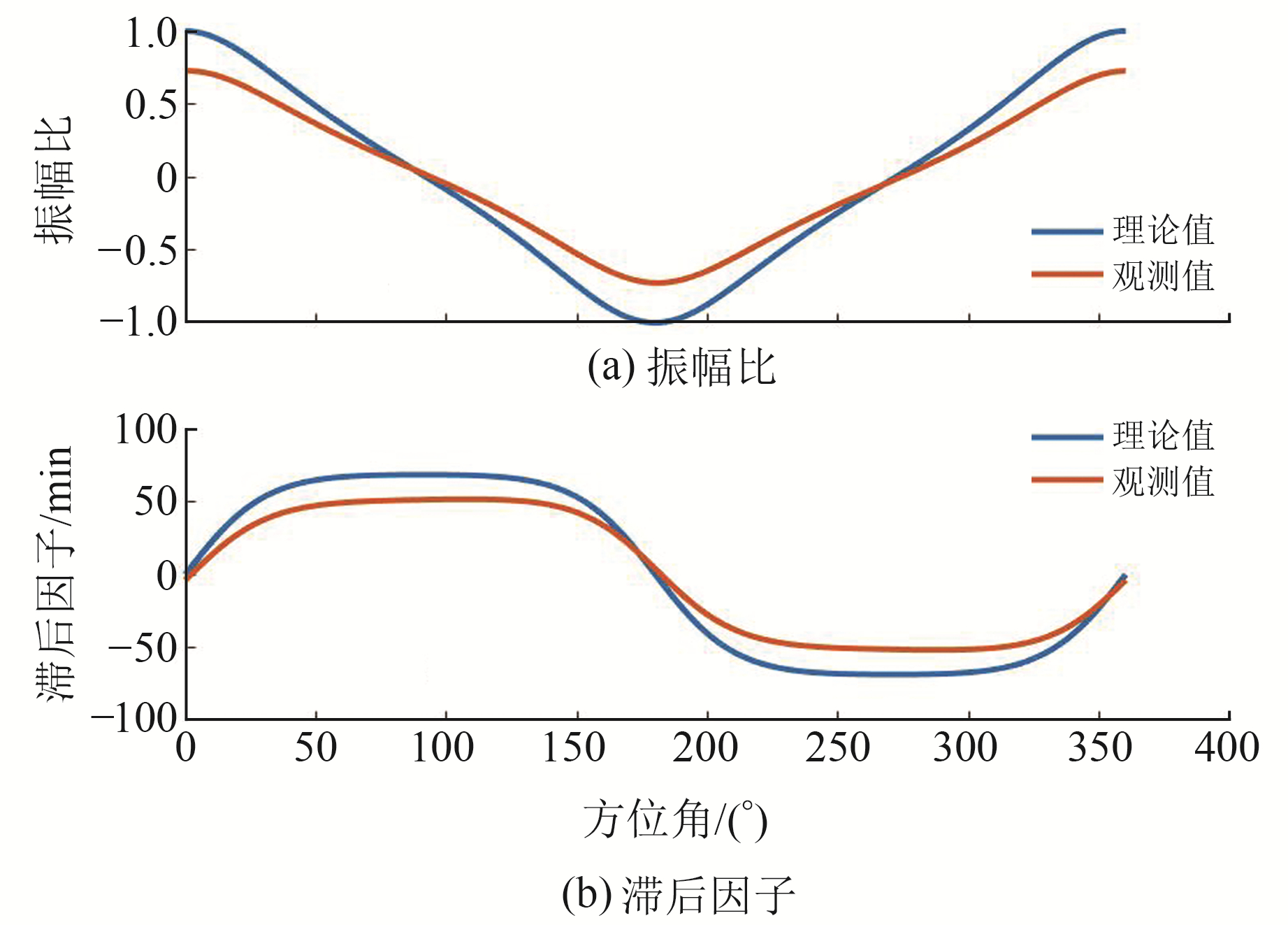
在0°~360°平面内,方位角A依次取0°、1°、2°、…359°将获得360组a、b值,结果见图 3和表 1,其中理论值计算结果以aL、bL表示,观测值计算结果以ag、bg表示。
|
图 3 理论值与观测值振幅比和滞后因子随方位角变化动态曲随线 Fig. 3 The dynamic curve of the amplitude ratio and hysteresis factor between theoretical and observed values as a function of azimuth angle |
|
|
表 1 理论值和观测值拟合结果 Tab. 1 Fitting results of theoretical and observational values |
由于理论值与观测值的真方位角AZ=0°,最佳拟合方位角AS=0°,本文重点分析AS=0°时拟合参数振幅比和滞后因子的特征。
对于理论值,由图 3和表 1可知,0°~360°内aL仅有1个极大值点,即0°时aL=1.0,而离开0°的所有aL值都小于1.0;bL的绝对值有2个极小值点,即0°和180°时bL=0.0。由此可知,NAKAI最佳拟合时aL应具有极大值,bL绝对值具有极小值且靠近aL的极大值点。
对于观测值,由图 3和表 1可知,0°~360°内ag仅有1个极大值点,即1°时ag=0.727;bg有2个极小值点,即2°和182°时bg=0.24。由ag的极大值得到ASA=1°,由靠近ASA的bg极小值点得到ASB=2°,但二者只能选其一,本文选AS=ASB=2°,理由是:在1°附近,ag的梯度绝对值da<0.001/°,表明ASA在1°附近变化非常缓慢,对应的AS将随a值发生变化;而在2°附近,bg的梯度值db≈1.75/°,计算过程收敛快、指向精准。
由此可知,基于NAKAI拟合方法确定视方位角的方法是:将计算理论值的方位角限定在±π内,以足够小的间隔计算出N组理论值,再分别与观测值进行NAKAI计算,给出a、b的N组序列值ag和bg;首先确定ag最大值点的方位角ASA,然后在ASA附近寻找bg的极小值点ASB,ASB即为该组数据的视方位角。
1.3 方位角偏差对NAKAI拟合结果的影响通过表 1方位角偏差理论值对应的拟合结果,进一步了解方位角偏差对NAKAI拟合结果的影响。由理论值拟合结果可知,当方位角偏差为10°时,拟合振幅比偏差约为3%,滞后因子约为20 min;当方位角偏差为20°时,拟合振幅比偏差约为12%,滞后因子约为39 min;当方位角偏差为45°时,拟合振幅比偏差约为44%,滞后因子约为63 min;当方位角偏差为90°时,拟合振幅比偏差约为97%,滞后因子约为68 min。表中观测值结果与理论值结果趋势相同,仅数值有所差别。
1.4 地倾斜视偏角基于理论值计算的视方位角ASL与真方位角AZ完全相等,而基于观测值计算的视方位角ASG与真方位角AZ则不相等,定义地倾斜视偏角为视方位角与真方位角之差,即视偏角PA=AS-AZ。图 1中理论值的视偏角为0°,观测值的视偏角为2°,由于地倾斜视偏角与视方位角之间仅相差一个常数(真方位角),因此视偏角的动态特征等于视方位角的动态特征,而视偏角的离散误差也等于视方位角的离散误差。
2 西拨子和兰州地倾斜视偏角计算结果为考察视方位角的长期稳定性,本文收集整理了北京延庆西拨子和甘肃兰州十里店地震台水管倾斜仪1987~2021年整点值观测数据,具体见表 2,其中2007~2021年数据来源于中国地震台网中心前兆台网部预处理数据库[9]。
|
|
表 2 水管倾斜观测数据概况及测向真方位角 Tab. 2 Overview of water pipe tilt observation data and true azimuth of measurement components |
首先将各测向分量数据按年分组,将每组数据按天分段,基于NAKAI公式每天得出1组结果,约定结果中的视方位角为aI,得到1 a中的N个序列A,再基于算术平均值原理计算出序列A的统计均值AS及统计误差MAS,其中MAS反映了序列A的离散情况,可利用其评价视方位角的稳定性。由于AS与MAS是基于年度序列值的统计结果,因此将其称为视方位角的年度统计均值和年度统计误差。
图 4为1988~2021年北京西拨子水管倾斜仪三分量年度视偏角方差的计算结果,图 5为1987~2020年兰州十里店水管倾斜仪两分量年度视偏角方差计算结果。

|
图 4 西拨子台三分量视偏角对比 Fig. 4 Comparison of the 3 component apparent declination angles of the Xibozi station |
|
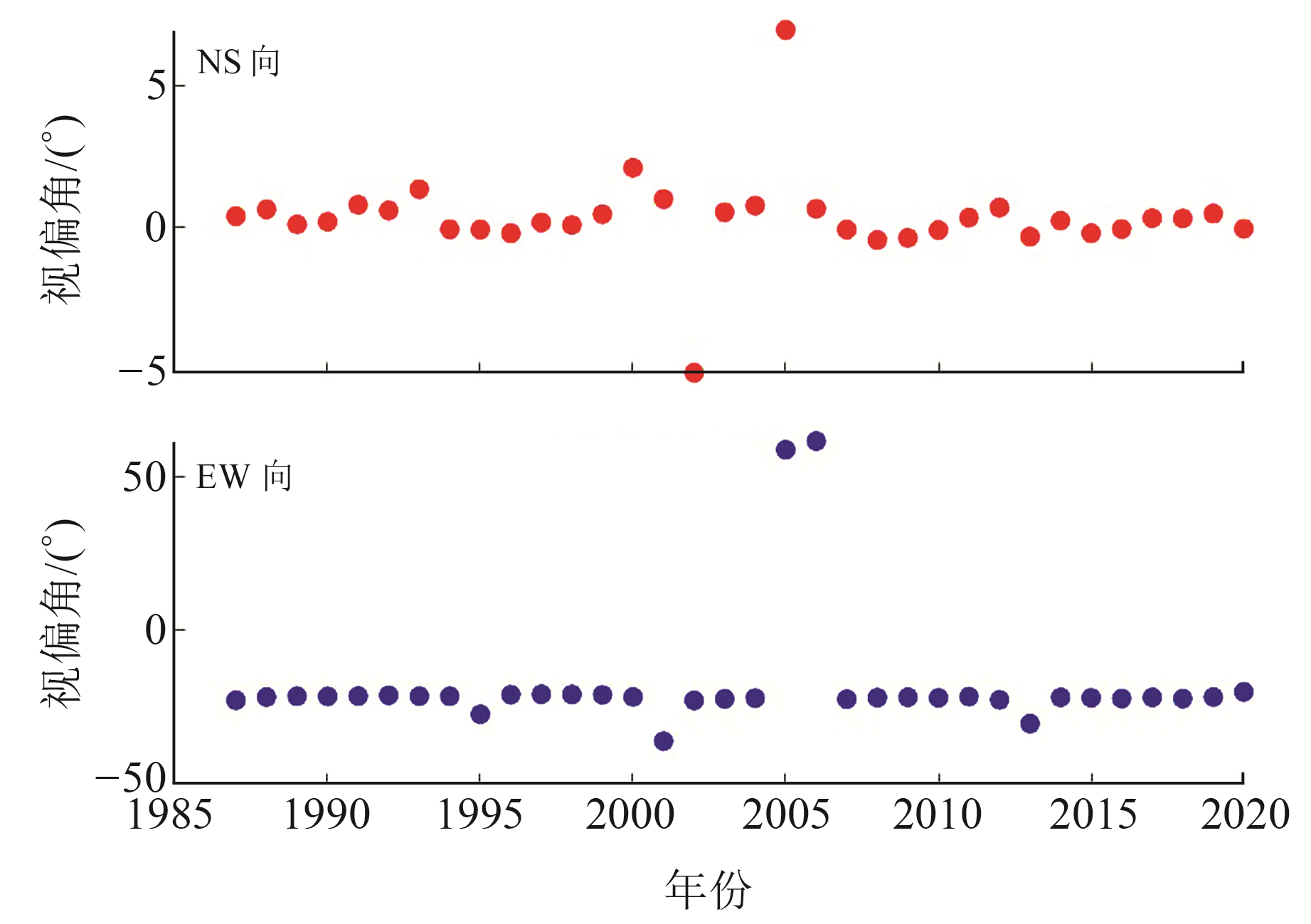
图 5 十里店台站两分量视偏角对比 Fig. 5 Comparison of the 2 component apparent declination angles at the Shilidian station |
图 4结果显示,NS向视偏角除1991年、2011年和2016年明显离群外,其余年度结果的最小值为-1.11°,最大值为3.24°,均值为-0.05°,年度之间的极差为4.35°;EW向除1998年和2021年显著离群外,其余年度结果最小值为-0.61°,最大值为23.2°,均值为9.59°,年度之间的最大极差为23.81°;NW向视偏角除1995年显著离群外,其余年度结果最小值为10.03°,最大值为14.7°,均值为12.22°,年度之间的最大极差为4.67°。
图 5结果显示,NS向视偏角除2002年和2005年显著离群外,其余年度结果最小值为-0.44°,最大值为2.1°,均值为0.33°,年度之间的极差为2.77°;EW向视偏角除2005年和2006年显著离群,其余年度结果最小值为-36.04°,最大值为-19.93°,均值为-22.54°,年度之间的极差为16.11°。
综合2个台站5个测向分量的视偏角结果来看,最大值可达23.2°,最小值为-36.04°,极差可达23.81°;均值最大值可达到12.22°,最小值为-22.54°。2个台均显示出NS向视偏角偏小、EW向和NW向视偏角偏大的特征。
3 全国地倾斜台网2020年度视偏角计算结果 3.1 数据概况为考察全国地倾斜台网视偏角年度结果的分布情况,从中国地震台网中心前兆台网部预处理数据库[9]收集到2020年地震地倾斜台网715个测向分量的整点值观测数据,覆盖全国205个台站,其中包括96个水平摆倾斜仪测向、281个垂直摆倾斜仪测向、259个水管倾斜仪测向及79个井下摆倾斜仪测向。
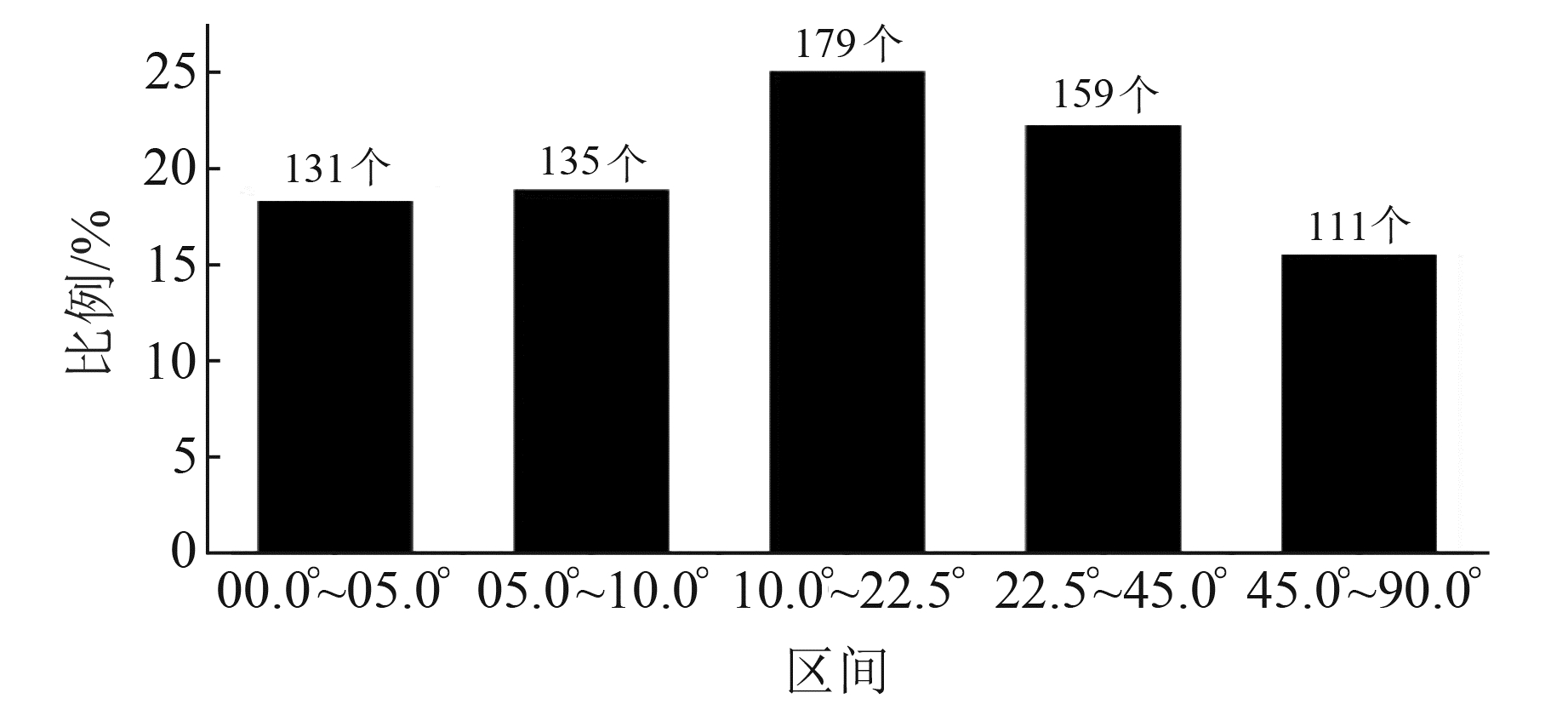
3.2 视偏角PS的大小分区统计结果图 6为各测向分量视偏角PS的大小分区统计结果,可以看出,PS<10°的分量数为265个,占37.20%;PS>22.5°的为270个,占37.76%;PS>45°的为111个,占15.52%。
|
图 6 2020年度视偏角PS的大小分区统计结果 Fig. 6 Size zoning statistics for the 2020 apparent declination PS |
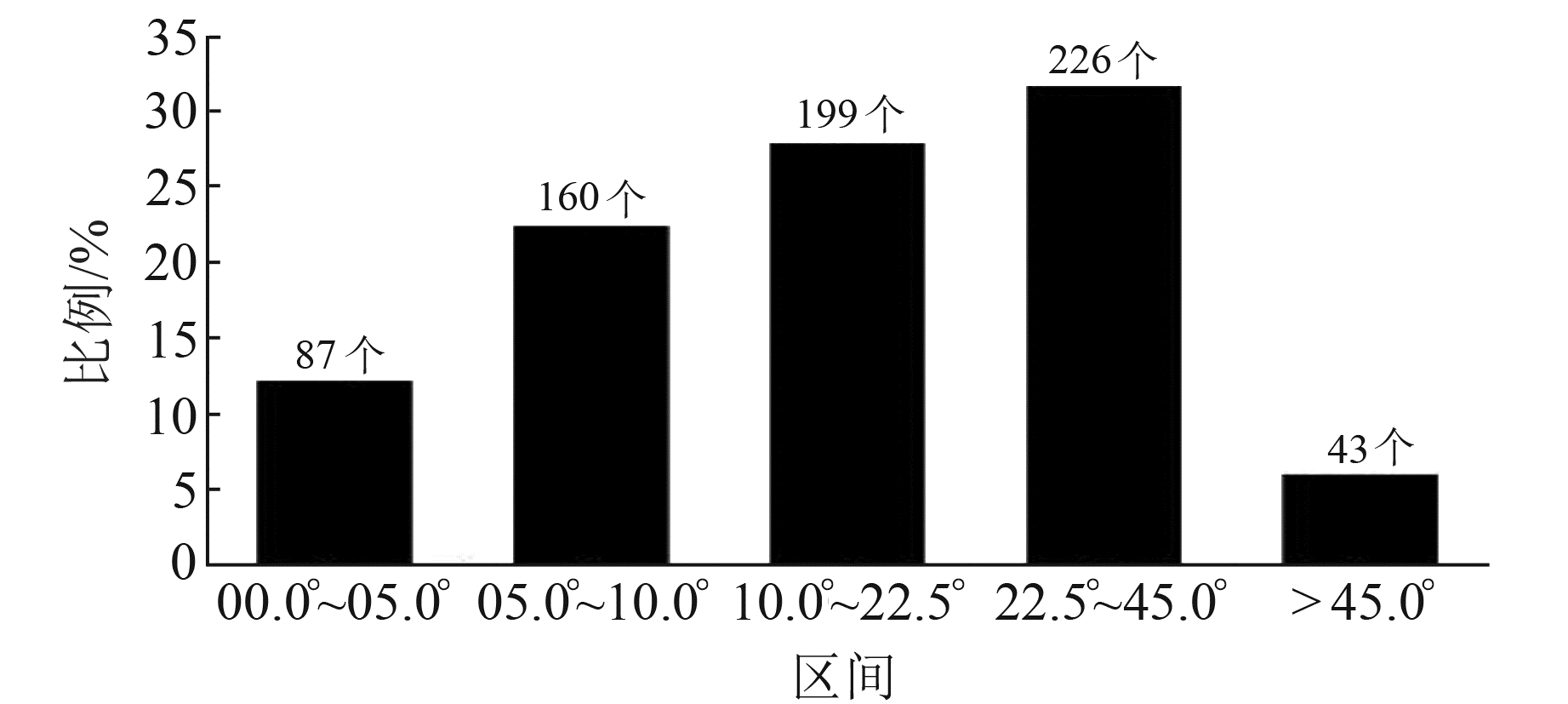
视偏角离散误差MPS反映了年度序列值的离散情况,图 7为视方位角离散误差的分区统计结果。由图可知,MPS<10°的分量数为247个,占34.55%;MPS<22.5°的为446个,占62.38%;MPS>45°的为43个,占6.01%。为直观展示视偏角的空间分布特征,分别绘制地倾斜各测向不同分量视偏角的空间分布(图 8~11),结果显示,4类仪器在NS向的结果优于EW向。
|
图 7 视偏角离散误差MPS的大小分区统计结果 Fig. 7 Statistical results of the size partition of the dispersion error MPS for visual declination |

|
图 8 水平摆倾斜结果分布 Fig. 8 Distribution of tilting results of horizontal pendulum |
|
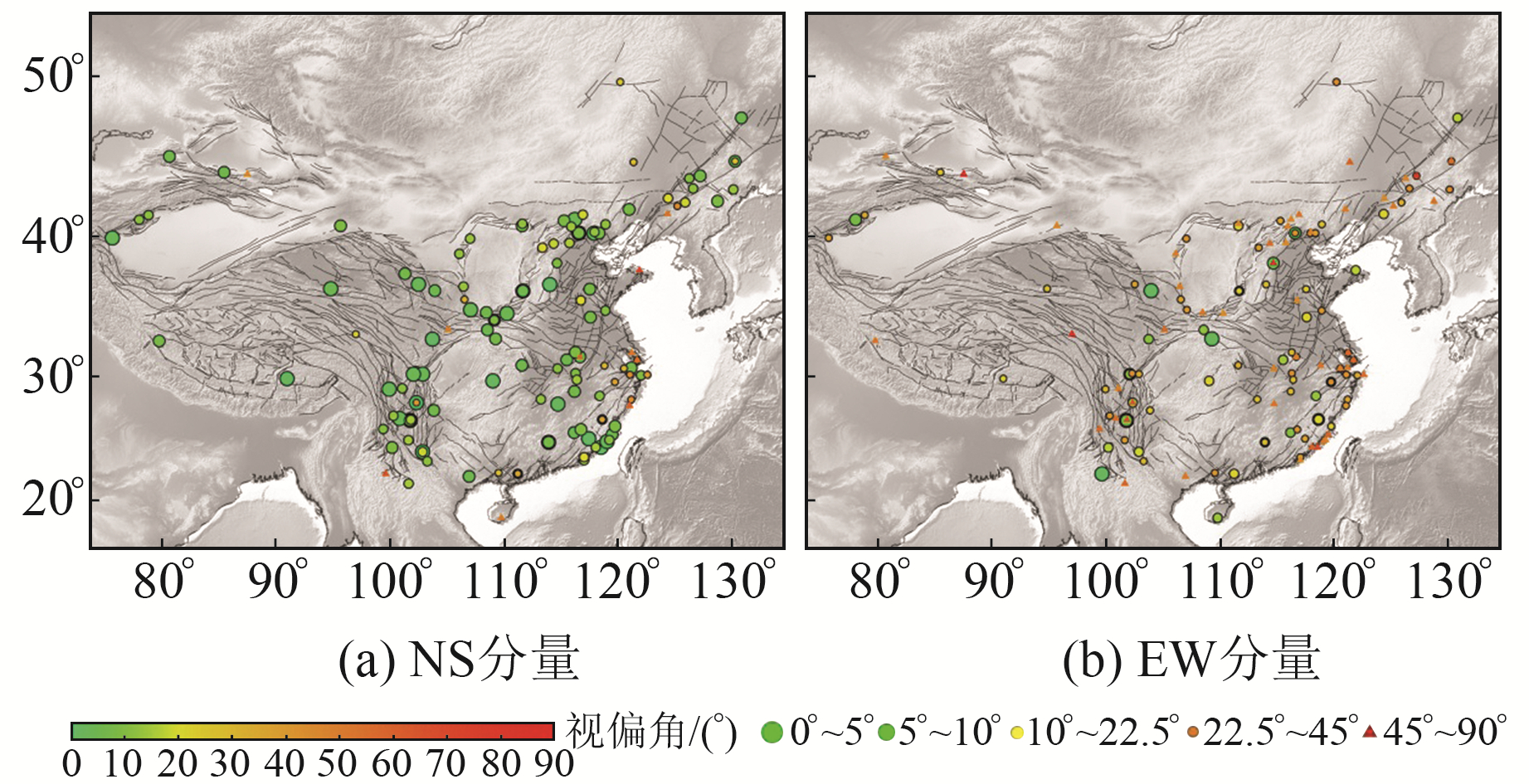
图 9 垂直摆倾斜仪结果分布 Fig. 9 Distribution of vertical pendulum tiltmeter results |

|
图 10 水管倾斜仪结果分布 Fig. 10 Distribution of water pipe tiltmeter results |

|
图 11 井下摆倾斜仪结果分布 Fig. 11 Distribution of underground pendulum tiltmeter results |
表 3为2020年16个视偏角PS>70°的测向分量数据,其中DT1和DT1M为基于方位角AZ0计算的振幅比及离散相对误差,DT2和DT2M为基于视方位角AZ2计算的振幅比及离散相对误差。由表可知,大同台14013J2251SH20的视偏角为87°,14013J2252SH20的视偏角为78.7°,这2个测向分量的DT1和DT1M都不正常,而DT2和DT2M均是正常的,可能是2个分量的输出端接反了;阳霞台情况与大同台类似。除去4个异常测向,其余12个测向分量的DT2及DT2M均优于DT1及DT1M,认为表4中16个测向分量的真方位角A0应当更接近于视方位角AS,而表中方位角A0的数据可能是错误的。结果表明,当视偏角出现异常(PS>45°)时,利用视方位角AS校核真方位角A0有一定的效果。
|
|
表 3 视偏角PS>70°的测向分量 Tab. 3 Measurement components with apparent deviation angle PS > 70° |
1) 基于NAKAI最佳拟合结果确定的地倾斜视方位角AS是地倾斜固体潮观测数据中的重要属性参数,可以判断起始方位角A0的准确性,并检验观测数据内在质量的可靠性;
2) 1987~2020年西拨子和十里店水管倾斜仪观测数据计算结果表明,西拨子NS向视偏角PNS=-0.1°,EW向视偏角PEW=9.6°,NE向视偏角PNE=12.4°;十里店NS向视偏角PNS=0.3°,EW向视偏角PEW=-22.5°。
3) 2020年全国地倾斜台网715个测向分量观测数据计算结果表明,视偏角PS<10°的分量数为266个,占37.20%;PS<22.5°的为445个,占62.24%;PS>45°的为111个,占15.52%;视偏角离散误差MPS<10°的分量数为247个,占34.55%;MPS<22.5°的为446个,占62.38%;MPS>45°的为43个,占6.01%。根据水平摆倾斜仪、垂直摆倾斜仪、水管倾斜仪及井下摆倾斜仪结果分布认为,四类仪器在NS向的结果优于EW向,垂直摆倾斜仪两分量的差异尤其明显,个别仪器的视偏角接近90°,需要重新筛查数据质量。
4) 当视方位角偏差为10°时,拟合振幅比偏差约为3%,滞后因子约为20 min;当视方位角偏差为20°时,拟合振幅比偏差约为12%,滞后因子约为39 min;当视方位角偏差为45°时,拟合振幅比偏差约为44%,滞后因子约为63 min;当视方位角偏差为90°时,拟合振幅比偏差约为97%,滞后因子约为68 min。因此,建议对于视偏角大于20°的测向分量的起始方位角应予以重点核查;对于视偏角离散误差大于20°的测向分量的观测数据应进行认真筛查。
5) 当视偏角出现异常(PS>45°)时,应首先核查使用的真方位角AZ0是否正确,此时利用视方位角AS校核方位角A0有一定的效果。
| [1] |
中国地震局. 地震与地震前兆预测分类与代码DB/T 3-2003[S]. 北京: 地震出版社, 2003 (China Earthquake Administration. Classification and Code for Earthquake and Earthquake Precursor Prediction—DB/T 3-2003[S]. Beijing: Seismological Press, 2003)
(  0) 0) |
| [2] |
中国地震局. 地震台站代码DB/T 4-2003[S]. 北京: 地震出版社, 2004 (China Earthquake Administration. Seismic Station Code-DB/T 4-2003[S]. Beijing: Seismological Press, 2004)
(  0) 0) |
| [3] |
陈德福. 我国的水管仪倾斜固体潮观测[C]. 2004年重力学与固体潮学术研讨会暨祝贺许厚泽院士70寿辰研讨会, 武汉, 2004 (Chen Defu. Inclined Earth Tide Observation with Water Tube Instrument in China[C]. 2004 Academic Conference on Gravity and Earth Tide and Seminar on the 70th Birthday of Academician Xu Houze, Wuhan, 2004)
(  0) 0) |
| [4] |
中国地震局. 地震及前兆数字观测技术规范-地壳形变观测: 试行[S]. 北京: 地震出版社, 2001 (China Earthquake Administration. Technical Specification for Digital Observation of Earthquakes and Precursors-Crustal Deformation Observation: Trial Implementation[S]. Beijing: Seismological Press, 2001)
(  0) 0) |
| [5] |
沈旭章, 唐九安, 高安泰. 固体潮观测数据处理手册[Z]. 广州: 中山大学出版社, 2022 (Shen Xuzhang, Tang Jiuan, Gao Antai. Solid Tide Observation Data Processing Manual[Z]. Guangzhou: Sun Yat-Sen University Press, 2022)
(  0) 0) |
| [6] |
唐九安. 固体潮观测数据的预处理[J]. 西北地震学报, 1981, 3(3): 73-77 (Tang Jiuan. The Pre-Processing Method of the Observation Data of Earth Tides[J]. Northwestern Seismological Journal, 1981, 3(3): 73-77)
(  0) 0) |
| [7] |
唐九安. 天顶距微分公式用于重力、倾斜和应变固体潮资料的拟合检验[J]. 地壳形变与地震, 1990, 10(2): 1-8 (Tang Jiu'an. The Zenith Distance Formulas of the First Order Differential Quotient for the Theoretic Value of the Earth Tides Applied to the Fit-Testing of the Gravity, Tilter and Line Strain Earth Tides[J]. Crustal Deformation and Earthquake, 1990, 10(2): 1-8)
(  0) 0) |
| [8] |
蒋骏, 张雁滨. 固体潮理论值一阶微商的解析表达式及拟合检验[J]. 地球物理学报, 1994, 37(6): 776-786 (Jiang Jun, Zhang Yanbin. A Differential Analytical-Representation of the Theoretical Value of Earth Tide and the Fit-Testing of Earth Tide Data[J]. Chinese Journal of Geophysics, 1994, 37(6): 776-786)
(  0) 0) |
| [9] |
陆忠远, 李胜乐, 邓志辉, 等. 基于GIS的地震分析预报系统[M]. 成都: 成都地图出版社, 2002 (Lu Zhongyuan, Li Shengle, Deng Zhihui, et al. Earthquake Analysis and Prediction System Based on GIS[M]. Chengdu: Chengdu Cartographic Publishing House, 2002)
(  0) 0) |
2. Southern Marine Science and Engineering Guangdong Laboratory(Zhuhai), North-Qinglü Road, Zhuhai 519000, China;
3. Gansu Earthquake Agency, 450 West-Donggang Road, Lanzhou 730000, China
 2024, Vol. 44
2024, Vol. 44


