近年来,水利工程建设得到快速发展,尤其是大坝建设数量日益增多,在带来巨大电能资源的同时,也会不同程度地抬高上游水位,诱发古滑坡复活,对航运安全造成巨大威胁,因此开展古滑坡复活变形特征分析及变形预测研究具有重要的现实意义[1-2]。部分学者[3-5]对古滑坡变形破坏机制及稳定性进行了分析,但未涉及库岸古滑坡的相关研究。一般来说,变形可很大程度上反映滑坡的稳定状态,亦可作为古滑坡复活的重要依据。因此,对古滑坡复活变形特征进行着重分析及预测具有重要意义。
在以往研究中,田倩等[6]通过神经网络构建古滑坡变形预测模型;宁波等[7]对组合预测模型在古滑坡变形预测中的适用性进行分析;赵瑛等[8]通过相关向量机评价古滑坡变形潜势。这些研究进一步说明开展古滑坡变形预测具有必要性,但研究未考虑变形数据的噪声信息,因此对古滑坡变形的预测研究仍有空间。
值得指出的是,在预测过程中,由于滑坡变形数据具有一定的噪声信息,有必要先对其进行分解处理,而小波包变换的数据分解能力强[9],相关向量机[10]、混沌理论[11]在滑坡变形预测中具有良好效果,可通过上述3种方法综合实现滑坡变形预测。本文以库岸古滑坡复活体为工程背景,结合现场调查成果及变形监测资料,依次分析古滑坡变形特征及预测结果,充分掌握其变形发展规律,以期为古滑坡复活防治提供指导。
1 基本原理本文结合滑坡处地质条件及调查成果,首先开展复活特征分析,再以变形监测成果为基础,通过小波包变换、相关向量机(relevance vector machine, RVM)及混沌理论(chaos theory, CT)等构建出预测模型,并以其开展变形预测,掌握其发展规律。
在监测过程中,由于滑坡现场不确定因素相对较多,其变形监测数据大多不能代表滑坡的真实变形值,会含有一定的噪声信息,因此将滑坡变形监测值Yi表示为:
| $ Y_i=Z_i+S_i $ | (1) |
式中,Zi为真实变形分量,代表滑坡真实变形值;Si为噪声,代表滑坡随机变形噪声值,由温度变化、仪器误差、人为因素等造成。
顾及噪声对预测精度具有较大影响[9],在构建变形预测模型前有必要先对其进行剔除处理。WPT是现阶段常用的信号提取方法,其能有效分解低频信号,并兼顾高频信号的分解,具有较优的分解能力。根据WPT的基本原理,可将其分解公式表示为:
| $ \left\{\begin{array}{l} d_{1 k}(j)=\sum\limits_k h_k d_k(j-1) \\ d_{2 k}(j)=\sum\limits_k g_k d_{2 k}(j-1) \end{array}\right. $ | (2) |
式中,d1k(j)、d2k(j)分别为分解后的低频、高频信号;k为平移参量;hk、gk为低频、高频滤波函数。跟据式(2)将滑坡变形数据分解为若干频率信号,再设定滤波界限,筛选出噪声信息,并对其余信号进行重构计算,即可将滑坡变形数据分解为真实变形分量和噪声。同时,提出利用信噪比(SNR)评价数据分解效果,其计算公式为:
| $ \mathrm{SNR}=10 \times\left(\frac{\text { Power }_s}{\text { Power }_n}\right) $ | (3) |
式中,Powers为变形监测数据的功率;Powern为变形监测数据过滤后的功率。由于已对滑坡变形数据进行分解处理,其后续预测模型也应进行针对性构建。
1.1 真实变形分量预测模型相关向量机是支持向量机的改进方法,其改进点主要为:核函数不再受Mercer理论限制,其稀疏性、鲁棒性相对更强。因此,提出利用相关向量机构建真实变形分量的预测模型。结合RVM原理,将其训练函数表示为:
| $ z_i=\sum\limits_{i=1}^N w_i k\left(x_i\right)+w_0+\varepsilon $ | (4) |
式中,zi为真实变形分量预测值;N为训练样本数;xi为输入信息;k(·)为核函数;wi、w0为权值向量;ε为初始高斯噪声。
研究成果表明[9],核函数的限制条件不足会对预测精度产生一定影响,有必要对其进行优化处理。考虑到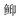
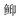
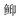
|
|
表 1 不同测试函数的寻优结果 Tab. 1 Optimization results of different test functions |
综合上述分析,将真实变形分量的预测模型确定为ROA-RVM模型。
1.2 噪声预测模型噪声一般具有混沌特征[12-13],因此提出利用混沌理论构建预测模型。先利用Lyapunov指数法计算混沌指数,若最大值大于0,说明可利用混沌理论实现噪声预测;反之,则不能。混沌指数计算公式为:
| $ \lambda=\frac{1}{t_M-t_0} \sum\limits_{i=0}^M \ln \frac{l_i}{L_i} $ | (5) |
式中,λ为混沌指数;M为计算频次;tM、t0为时间参量;li为重构后的距离;Li为初始距离。
在验证噪声存在混沌特征的基础上,引入延迟时间并嵌入维数参数,以实现噪声的空间重构处理。由此可见,延迟时间和嵌入维数参数对噪声预测具有显著影响,结合以往研究成果[14],利用去偏复自相关法和C-C法分别计算参数。
以相空间中ψi节点为中心,将其与相邻点ψj间的距离d表示为:
| $ d=\min\limits_j\left\|\psi_i-\psi_j\right\|=\left\|\psi_i-\psi_l\right\| $ | (6) |
当保证ψi、ψj间距相邻且d值最小时,利用反推计算即可实现对噪声的预测处理。
综上可知,变形预测模型最终设定为WPT-ROA-RVM-CT模型。在预测结果中,利用相对误差评价预测精度,其值越小,说明预测精度越好;反之,预测精度越差。
2 实例分析 2.1 工程概况 2.1.1 项目区工程地质条件1) 地形地貌。滑坡区具侵蚀中低山地貌,高程分布范围介于300~895 m,地形起伏较大,大致呈后缘陡、前缘缓的特征。区内冲沟较发育,走向大致呈NS向,多为季节性冲沟,其切割深度多介于30~60 m,沟道上游陡,具“V”形特征,下游较缓,具“U”形特征。
2) 地层岩性。滑坡区第四系地层成因较多,主要可分为堆积层、冲洪积层、崩坡积层,各类地层性质差异较大。下覆基岩为沙溪庙组泥岩,紫红色,产状为354°∠30°,节理裂隙较发育,地层埋深越浅其裂隙发育相对越多,岩体完整性相对略差;埋深越深,裂隙发育相对越少,岩体完整性也越好。
3) 地质构造。滑坡区位于大型褶皱构造东翼,距滑坡核部约3.4 km。由于构造发育,很大程度上影响区内地层结构的完整性,且据调查成果可知,区内节理一般具网状特征,长度较短,多由泥质物充填。
4) 水文地质条件。区内地表水主要为滑坡前缘常年的河道流水,其水位具有一定的季节性波动特征,即本文实例对象具库岸滑坡特征;除此之外,滑坡地表发育较多冲沟,以季节性流水为主,流量变化差异大。地下水类型主要为孔隙水、裂隙水,其中孔隙水赋存于第四系地层孔隙中,水力联系相对较差,受地形影响,无统一水面;裂隙水赋存于基岩裂隙中,其富水性受构造影响较大,与上部孔隙水具有一定的水力联系。
通过上述分析可知,滑坡区地质条件相对较为一般,为滑坡灾害的发育奠定了基础条件。
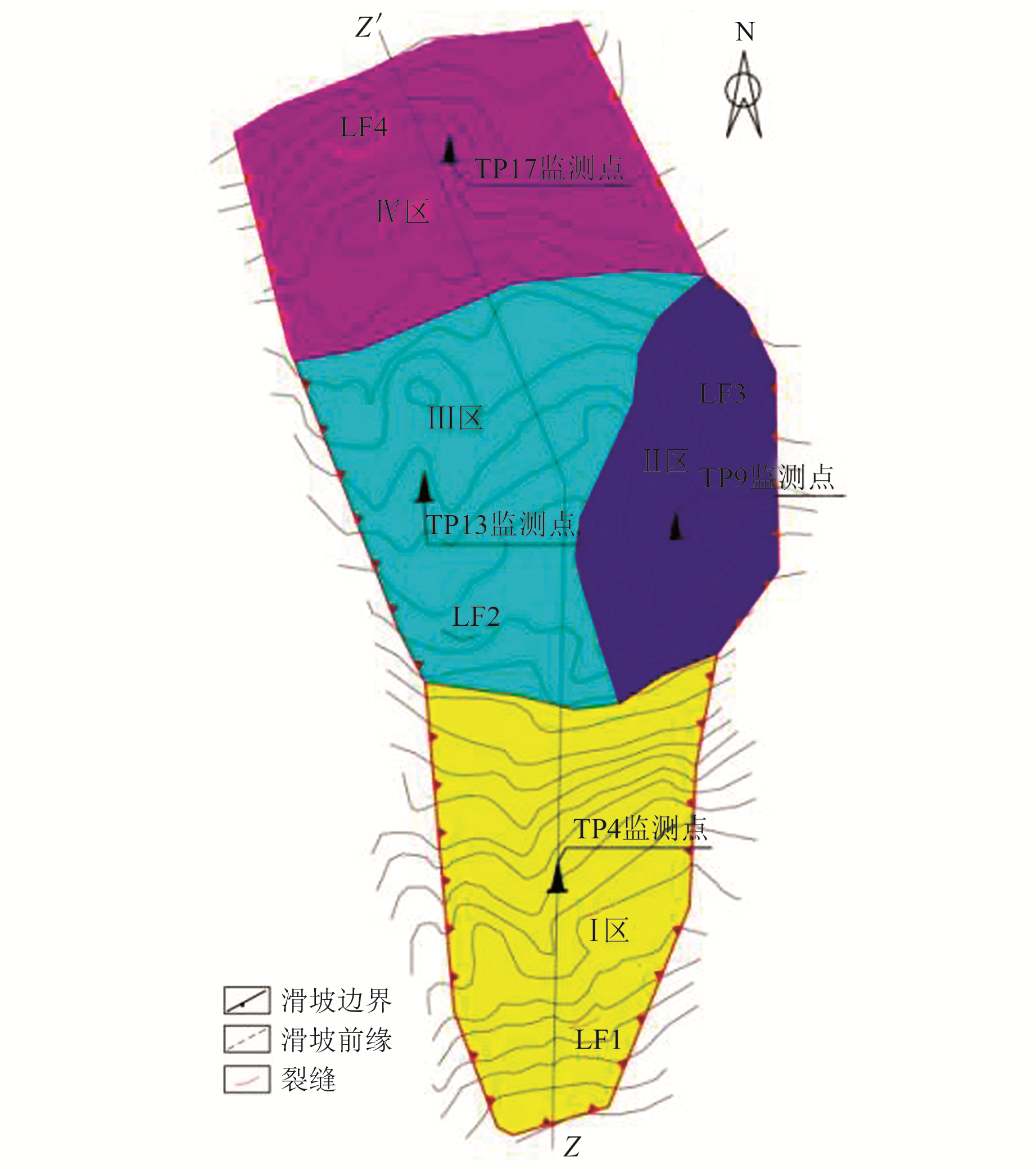
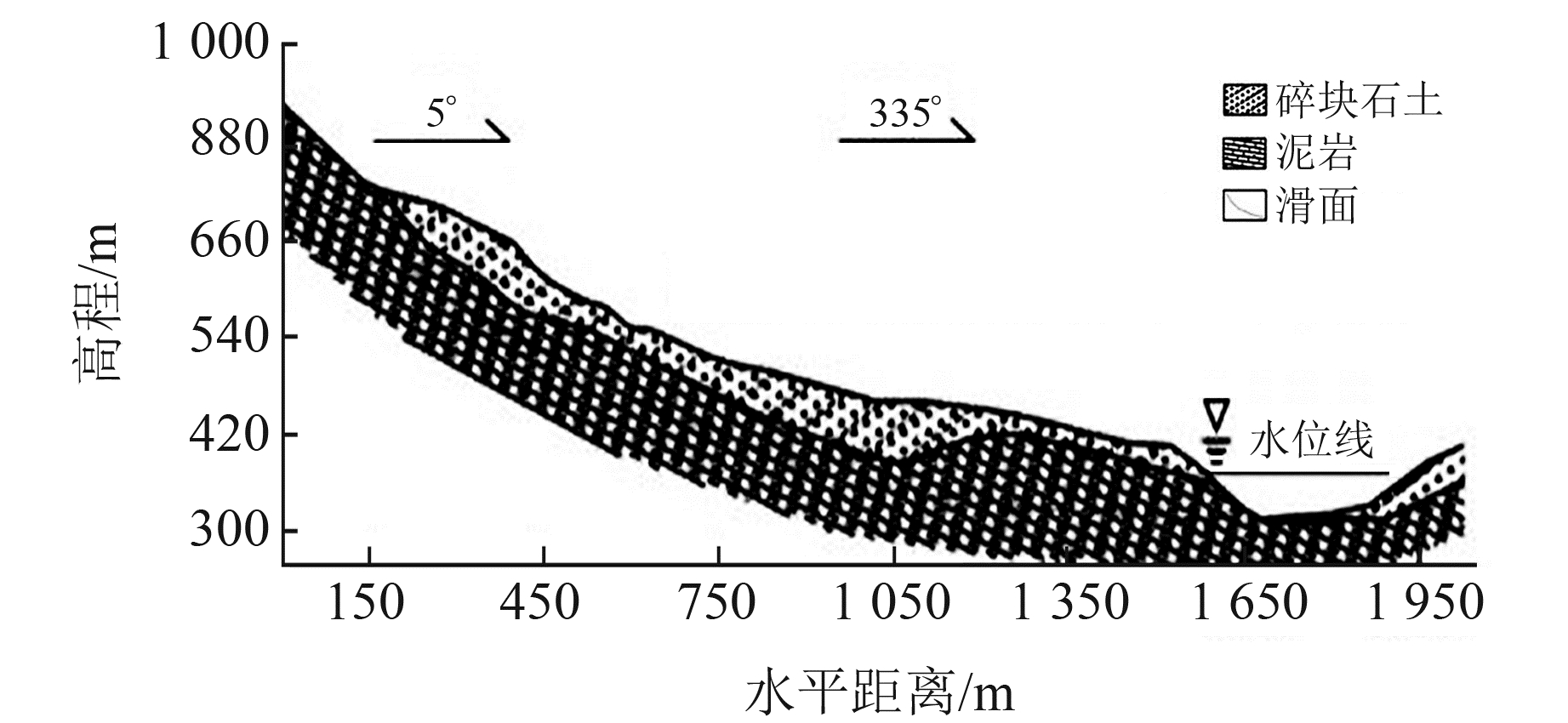
2.1.2 滑坡发育条件通过对滑坡区样品进行14C实验,测得滑坡堆积物形成年代为2 850 a BP,该滑坡属古滑坡范畴。研究区复活部分在平面上具南窄北宽条带状特征(图 1),主滑方向为5°转355°,结合下覆基岩产状,该滑坡具有典型的顺层滑坡特征。滑坡纵向长度约1 500 m,横向宽度介于300~700 m之间,平面面积约75 km2,平均厚度约30 m,体积约2 250×104 m3,因此该滑坡属特大型顺层滑坡。滑坡主滑面(Z-Z′剖面)示意图见图 2。
|
图 1 滑坡平面示意图 Fig. 1 Schematic diagram of landslide |
|
图 2 Z-Z′剖面示意图 Fig. 2 Schematic diagram of Z-Z′ section |
本文研究对象是古滑坡复活体,为进一步掌握古滑坡的复活特征,结合现场变形监测数据和调查结果,重点开展复活体变形特征分析。同时,为便于后续描述,结合复活体特征,将其划分为Ⅰ~Ⅳ区,具体划分见图 1。
2.2.1 地表裂缝发育特征通过现场勘查可知,古滑坡复活变形2011年就已开始,其后历年均有不同规模的裂缝发育,且变形特征并无特殊规律。限于篇幅,从4个区各挑选1个2019年以来最具代表性的裂隙进行描述,裂缝位置见图 1。
LF1:该裂缝位于Ⅰ区,其延伸长度约86 m,延伸方向近EW向,张开宽度约6~14 cm,可见深度约1.6 m,具有明显下错特征,下错高度多介于40~74 cm。
LF2:该裂缝位于Ⅲ区,其延伸长度约65 m,延伸方向也近EW向,张开宽度约10~30 cm,可见深度约2.3 m,下错特征一般,下错高度多介于15~30 cm。
LF3:该裂缝位于Ⅱ区,其延伸长度约122 m,延伸方向近NS向,张开宽度约23~35 cm,可见深度约1.8 m,下错特征较强,下错高度多介于30~67 cm。
LF4:该裂缝位于Ⅳ区,其延伸长度约94 m,延伸方向近似EW向,张开宽度约15~20 cm,可见深度约1.1 m,下错特征一般,下错高度多介于5~15 cm。
总体来说,滑坡区地表裂缝发育特征显著,以张剪性质为主,事件发生时间主要集中在强降雨或持续降雨后,因此降雨是地表裂缝产生的主要诱因。
2.2.2 地表变形特征在滑坡地表布设21个监测点用于监测地表总位移,其中Ⅰ区布设TP1~TP6共6个监测点,Ⅱ区布设TP7~TP11共5个监测点,Ⅲ区布设TP12~TP16共5个监测点,Ⅳ区布设TP17~TP21共5个监测点。将监测时间确定为2020-01~2022-12,对每个区相应监测点数据进行均值求解,并进行水平、垂直位移分解,以便进行后续整体分析。同时,为顾及季节对滑坡变形的影响,将分析过程划分为旱季变形特征和雨季变形特征。
首先,统计得到滑坡地表旱季变形特征参数,结果见表 2。由表可知,4个分区的水平和垂直变形分量具有不同的特征参数值,Ⅰ~Ⅲ区变形值相对最大,Ⅳ区变形值相对最小,且该区与其他区的差异较为明显。因此,在旱季时,滑坡中后部形变相对更大,明显大于滑坡前缘。对比两个方向的变形分量可知,水平变形分量明显大于垂直变形分量,即滑坡变形以水平变形为主。就水平变形分量的方位角变化而言,2020~2022年4个分区的水平变形方向呈现逆时针变化特征。
|
|
表 2 滑坡地表旱季变形特征 Tab. 2 Characteristics of deformation of landslide surface during dry season |
其次,统计得到滑坡地表雨季变形特征参数,结果见表 3。由表可知,Ⅰ区变形量明显最大,其次为Ⅱ区和Ⅲ区,Ⅳ区变形量最小,说明在滑坡地表雨季变形结果中,从滑坡后缘至前缘变形量逐步减小;同时,水平变形分量也明显大于垂直变形分量,且水平变形分量的方位角变化也与旱季相同,具逆时针变化特征。
|
|
表 3 滑坡地表雨季变形特征 Tab. 3 Characteristic of deformation of landslide surface during rainy season |
由滑坡地表旱季及雨季变形特征可知,滑坡具有明显推移式特征,变形特征较为显著,说明古滑坡复活明显,也从侧面验证了开展滑坡后续变形预测研究的必要性。
2.2.3 时间-变形特征为进一步掌握复活体的变形特征,在4个分区中部各选择1个监测点进行时间-变形特征分析,即利用TP4、TP9、TP13及TP17监测点(各监测点分布位置见图 1)进行分析。在滑坡变形监测过程中,统计频率为1次/月,统计时间为2020-01~2022-12,共得到36期地表变形数据。
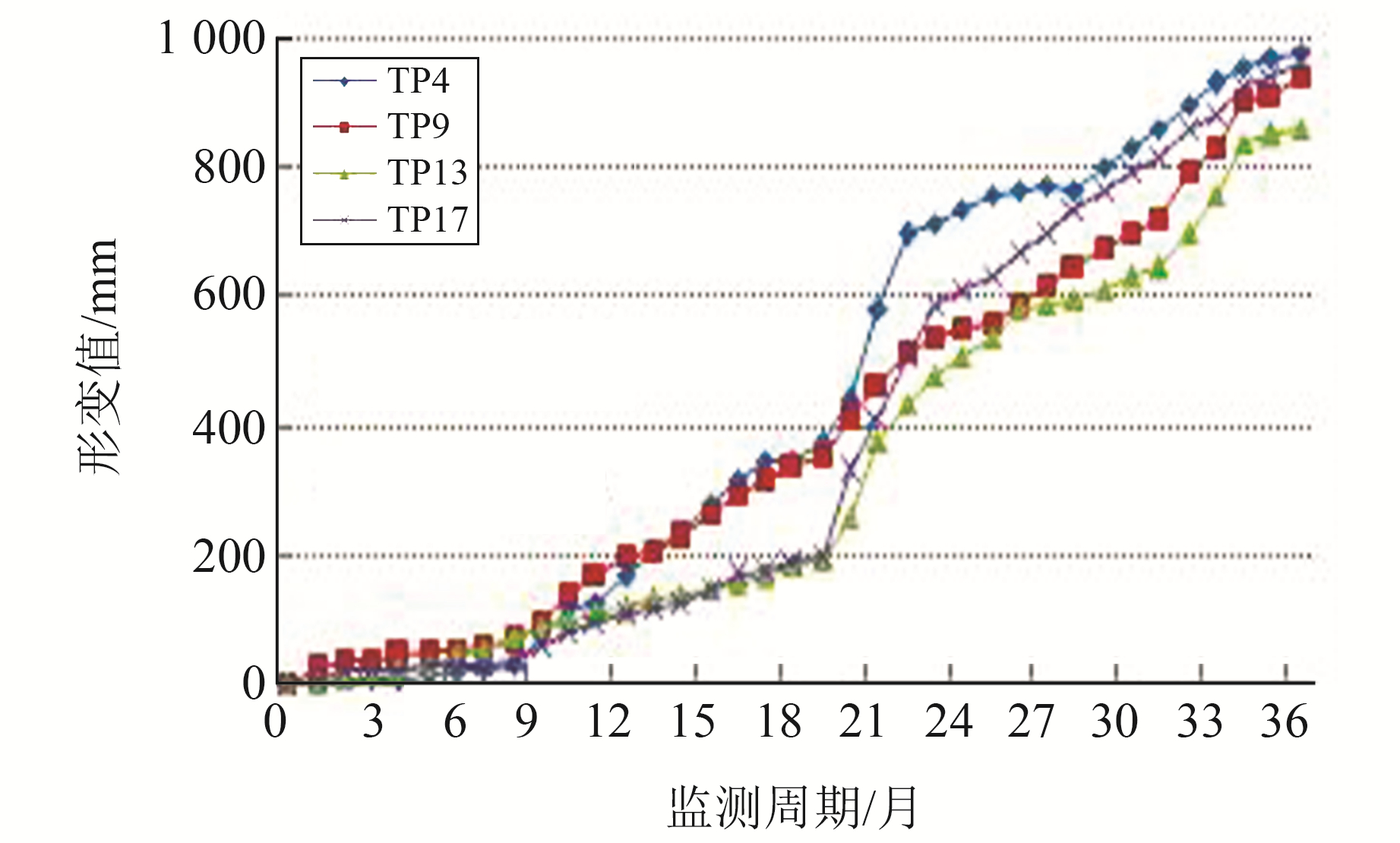
经统计得到4个监测点的时间-变形曲线结果见图 3。由图可知,随着时间的推移,滑坡地表形变呈持续增加特征,仅线型陡缓存在差异,应是受降雨因素的影响。再对4个监测点的变形速率特征值进行统计,得到其特征参数。其中,TP4监测点变形速率介于1.32~144.16 mm/月,平均值为27.26 mm/月;TP9监测点变形速率介于1.14~76.01 mm/月,平均值为26.24 mm/月;TP13监测点变形速率介于1.67~120.92 mm/月,平均值为23.95 mm/月;TP17监测点变形速率介于0.91 mm~126.76 mm/月,平均值为26.69 mm/月。
|
图 3 滑坡地表时间-变形曲线 Fig. 3 Time-deformation curve of landslide surface |
综上可知,在3 a监测过程中,滑坡累积变形量均偏大,且变形速率波动范围较大,进一步说明该滑坡变形特征显著。
2.3 滑坡变形预测研究利用WPT-ROA-RVM-CT模型开展滑坡变形预测研究。在预测过程中,以TP4、TP9、TP13及TP17监测点的监测结果作为后续数据分析来源,将前31期数据作为训练样本,32~36期数据作为验证样本。
首先,利用WPT开展滑坡变形数据的分解处理,且为验证WPT的分解能力,引入EMD、Kalman滤波开展同样的分解处理,得到WPT的SNR值为36.49 dB,EMD的SNR值为30.45 dB,Kalman滤波的SNR值为26.92 dB。WPT的SNR值相对较大,说明其分解效果相对最优,表明将其作为滑坡变形数据的分解处理模型具有合理性。
通过WPT将滑坡变形数据分解为真实变形分量和噪声,再采用ROA-RVM-CT模型开展分项预测,顾及到该模型具有多阶段组合特征,先以TP4监测点为例进行分析。计算统计得到TP4监测点的真实变形分量在优化前后的预测结果(表 4),由表可知,RVM模型的相对误差介于2.98%~3.35%之间,平均值为3.15%;ROA-RVM模型的相对误差介于2.59%~2.82%之间,平均值为2.68%。对比两者结果可知,经ROA优化处理能有效提高预测精度,表明ROA-RVM模型对滑坡真实变形分量具有适用性。
|
|
表 4 TP4监测点的真实变形分量预测结果 Tab. 4 Prediction results of real deformation component of TP4 monitoring point |
在TP4监测点真实变形分量预测的基础上,进一步通过CT开展噪声预测,得到TP4监测点的最终预测结果(表 5)。由表可知,经混沌理论的补充预测,得到预测结果的相对误差介于2.08%~2.16%之间,平均值为2.12%,即混沌理论能进一步提高TP4监测点的预测精度,验证了该方法的有效性。
|
|
表 5 TP4监测点的最终预测结果 Tab. 5 Final prediction results of TP4 monitoring point |
TP4监测点的预测结果充分验证了WPT-ROA-RVM-CT模型的预测能力,再利用其开展其他监测点的变形预测,结果见表 6。TP9监测点的相对误差介于2.06%~2.24%之间,平均值为2.15%;TP13监测点相对误差介于2.08%~2.23%之间,平均值为2.14%;TP17监测点相对误差介于2.02%~2.21%之间,平均值为2.11%。4个监测点的预测精度相当,充分验证了WPT-ROA-RVM-CT模型的变形预测能力。
|
|
表 6 4个监测点的最终变形预测结果 Tab. 6 Final deformation prediction results of four monitoring points |
以表 6中预测结果进行外推,对37~40期预测速率进行均值求解,并将其命名为后续变形速率均值,以掌握滑坡后续变形发展规律。经统计可知,TP4监测点的后续变形速率均值为6.92 mm/月,TP9监测点的后续变形速率均值为4.98 mm/月,TP13监测点的后续变形速率均值为3.76 mm/月,TP17监测点的后续变形速率均值为4.72 mm/月,4个监测点的后续变形速率均为正值且较大。因此,判断滑坡后续变形速率大,具有较大的失稳风险,需要尽快开展防治措施研究。
3 结语通过对特大型顺层古滑坡复活变形特征进行分析并对变形预测进行研究,得出以下结论:
1) 滑坡区地表裂缝发育特征显著,以张剪性质为主,事件发生主要集中在强降雨或持续降雨后,因此降雨是地表裂缝产生的主要诱因。
2) 在本文监测时段内,滑坡具有明显推移式特征,即滑坡中、后缘变形明显大于前缘,且变形方向具有逆时针变化特征,说明古滑坡复活明显,变形特征显著。
3) 变形预测结果验证了WPT-ROA-RVM-CT模型的预测能力,且通过外推预测,滑坡后续变形速率均为正值且较大,判断滑坡后续变形速率较大,具有较大的失稳风险。
| [1] |
孙昊, 李天涛, 裴向军, 等. 青海隆务西山古滑坡群复活机理及威胁范围预测[J]. 工程地质学报, 2022, 30(3): 829-842 (Sun Hao, Li Tiantao, Pei Xiangjun, et al. Revitalization Mechanism and Threat Range Prediction of Longwuxishan Ancient Landslide Group, Qinghai Province[J]. Journal of Engineering Geology, 2022, 30(3): 829-842)
(  0) 0) |
| [2] |
董文萍. 向家坝库区某大型顺层滑坡复活机制研究[D]. 郑州: 华北水利水电大学, 2019 (Dong Wenping. Research on Reactivation Mechanism of a Large Bedding Landslide in Xiangjiaba Reservoir[D]. Zhengzhou: North China University of Water Resources and Electric Power, 2019)
(  0) 0) |
| [3] |
宋国虎, 杨桢贤, 郭朝旭, 等. 成都五家坟滑坡变形破坏特征和复活机制分析[J]. 科学技术与工程, 2022, 22(2): 496-503 (Song Guohu, Yang Zhenxian, Guo Chaoxu, et al. Analysis on Deformation Characteristics and Resurrection Mechanism of Wujiafen Landslide[J]. Science Technology and Engineering, 2022, 22(2): 496-503)
(  0) 0) |
| [4] |
张永双, 吴瑞安, 任三绍. 降雨优势入渗通道对古滑坡复活的影响[J]. 岩石力学与工程学报, 2021, 40(4): 777-789 (Zhang Yongshuang, Wu Ruian, Ren Sanshao. Influence of Rainfall Preponderance Infiltration Path on Reactivation of Ancient Landslides[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(4): 777-789)
(  0) 0) |
| [5] |
刘江伟, 王运生, 金刚, 等. 甘草村古滑坡形成机制及堆积体稳定性分析[J]. 中国科技论文, 2020, 15(9): 1 019-1 025 (Liu Jiangwei, Wang Yunsheng, Jin Gang, et al. Formation Mechanism of Gancaocun Ancient Landslide and Analysis of Accumulation Body Stability[J]. China Sciencepaper, 2020, 15(9): 1 019-1 025)
(  0) 0) |
| [6] |
田倩, 吴健, 赵东. 基于神经网络和多标度特征分析的古滑坡变形预测及趋势评价[J]. 大地测量与地球动力学, 2022, 42(10): 1 056-1 062 (Tian Qian, Wu Jian, Zhao Dong. Deformation Prediction and Trend Evaluation of Paleo-Landslide Based on Neural Network and Multi-Scale Feature Analysis[J]. Journal of Geodesy and Geodynamics, 2022, 42(10): 1 056-1 062)
(  0) 0) |
| [7] |
宁波, 刘玉健, 王安东. 巨型古滑坡的稳定性评价及发展趋势分析[J]. 大地测量与地球动力学, 2022, 42(5): 515-519 (Ning Bo, Liu Yujian, Wang Andong. Stability Evaluation and Development Trend Analysis of Giant Ancient Landslide[J]. Journal of Geodesy and Geodynamics, 2022, 42(5): 515-519)
(  0) 0) |
| [8] |
赵瑛, 王显彪, 陈菊林, 等. 古滑坡活动诱发次级滑坡的稳定性评价及变形潜势分析[J]. 三峡大学学报: 自然科学版, 2022, 44(3): 27-33 (Zhao Ying, Wang Xianbiao, Chen Julin, et al. Stability Evaluation and Deformation Potential Analysis of Secondary Landslide Induced by Ancient Landslide Activity[J]. Journal of China Three Gorges University: Natural Sciences, 2022, 44(3): 27-33)
(  0) 0) |
| [9] |
陈金红, 崔东文. 基于小波包变换的ROA-ELM大坝变形多步预测模型[J]. 三峡大学学报: 自然科学版, 2022, 44(6): 21-27 (Chen Jinhong, Cui Dongwen. Multi-Step Prediction Model of ROA-ELM Dam Deformation Based on Wavelet Packet Transform[J]. Journal of China Three Gorges University: Natural Sciences, 2022, 44(6): 21-27)
(  0) 0) |
| [10] |
李晓斌. 基于极限位移准则和变形预测的滑坡变形潜势分析[J]. 大地测量与地球动力学, 2022, 42(6): 588-593 (Li Xiaobin. Analysis of Landslide Deformation Potential Based on Limit Displacement Criterion and Deformation Prediction[J]. Journal of Geodesy and Geodynamics, 2022, 42(6): 588-593)
(  0) 0) |
| [11] |
黄鑫, 权朝斌, 王辉, 等. 多维关联因素筛选条件下的堆积层滑坡体积预测研究[J]. 河南科学, 2020, 38(4): 645-653 (Huang Xin, Quan Chaobin, Wang Hui, et al. The Prediction of Landslide Volume of Accumulation Layer under the Condition of Multi-Dimensional Correlation Factor Screening[J]. Henan Science, 2020, 38(4): 645-653)
(  0) 0) |
| [12] |
郝付军. 运营桥梁的变形程度评价和预测分析[J]. 噪声与振动控制, 2022, 42(4): 121-126 (Hao Fujun. Evaluation and Prediction Analysis of Deformation Degree of Existing Bridges[J]. Noise and Vibration Control, 2022, 42(4): 121-126)
(  0) 0) |
| [13] |
黄阿岗, 何军, 郝付军. 基于混沌-RF-SVM变形预测模型的隧道运营安全状况分析[J]. 测绘工程, 2022, 31(4): 52-56 (Huang Agang, He Jun, Hao Fujun. Safety Analysis of Tunnel Operation Based on Chaos-RF-SVM Deformation Prediction Model[J]. Engineering of Surveying and Mapping, 2022, 31(4): 52-56)
(  0) 0) |
| [14] |
李锐鹏, 张宁晓, 魏中凯. 顾及混沌特征识别的黄土滑坡变形预测与稳定性评价[J]. 河南科学, 2022, 40(11): 1 802-1 810 (Li Ruipeng, Zhang Ningxiao, Wei Zhongkai. Deformation Prediction and Stability Evaluation of Loess Landslide Considering Chaotic Feature Identification[J]. Henan Science, 2022, 40(11): 1 802-1 810)
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44

