2. 中国地震局地震大地测量重点实验室,武汉市洪山测路40号,430071
钻孔应变仪一般安装于地下数十米深的基岩(或土层)中,可连续观测地层内部应变状态,具有数据精度高、观测频带宽、受地形限制少、安装方便、维护简单等优点,已成为主要的地壳应变观测仪器[1]。1968-09美国卡内基研究所的Sacks和得克萨斯大学的Evertson研制出世界上第一台钻孔(体)应变仪[2],随后钻孔应变仪在中国、日本等国家先后被研制出来,并得到迅速发展和完善,出现了三分量、四分量钻孔应变仪。经过几十年的发展,如今的钻孔应变仪已经能够观测到地震的同震、静态应变变化,被广泛应用于地震预报预警及震级估计等方面[3-6]。
对地震破裂过程的探讨一直都是地震学研究的热点。目前对地震破裂过程反演的研究已相对成熟,所用的数据也从最初的单一(GPS、InSAR和地震仪等)数据发展到多源数据[7]。而钻孔应变观测因其近年来表现出的巨大优势[8],被越来越多的学者应用于地震破裂研究。我国四分量钻孔应变观测技术已相对成熟,观测数据基本满足自洽,站点数量也能满足要求。本文以2022年门源MS6.9地震为例,通过分析四分量钻孔应变仪记录的观测值与计算的应变模拟值之间的相关性,探索钻孔应变观测数据约束地震破裂过程的可行性。
1 同震应变观测数据处理据中国地震台网中心(CENC)测定,北京时间2022-01-08 01:45:27青海省海北藏族自治州门源县(37.77°N,101.26°E)发生MS6.9地震,震源深度10 km。美国地质调查局(USGS)给出的地震初始破裂点为37.828°N、101.290°E,地震矩大小为1.046×1019 Nm,震级为MW6.6,震源深度为11.5 km,震源机制走向为104°、倾角为88°、滑动角为15°。全球矩心矩张量(GCMT)项目给出的地震起始破裂点为37.81°N、101.31°E,震级MW6.7,震源深度13.7 km,震源机制走向为105°、倾角为82°、滑动角为1°。
本文选取门源、湟源等17个钻孔应变仪台站2022-01-08 00:00:00~23:59:59的1 sps(samples per second)采样数据展开研究。为保证数据质量,对原始观测数据的4个分量进行去除突跳和有效插值预处理。
1.1 时间校正时间的准确性直接关系到数据的可信度。当钻孔应变仪台站GPS信号微弱时,难以保证仪器时间与实际时间完全一致,这时就需要对仪器进行时间校正[9]。通常P波的初至时刻比较清晰,本文利用发震后P波走时进行时间校正。
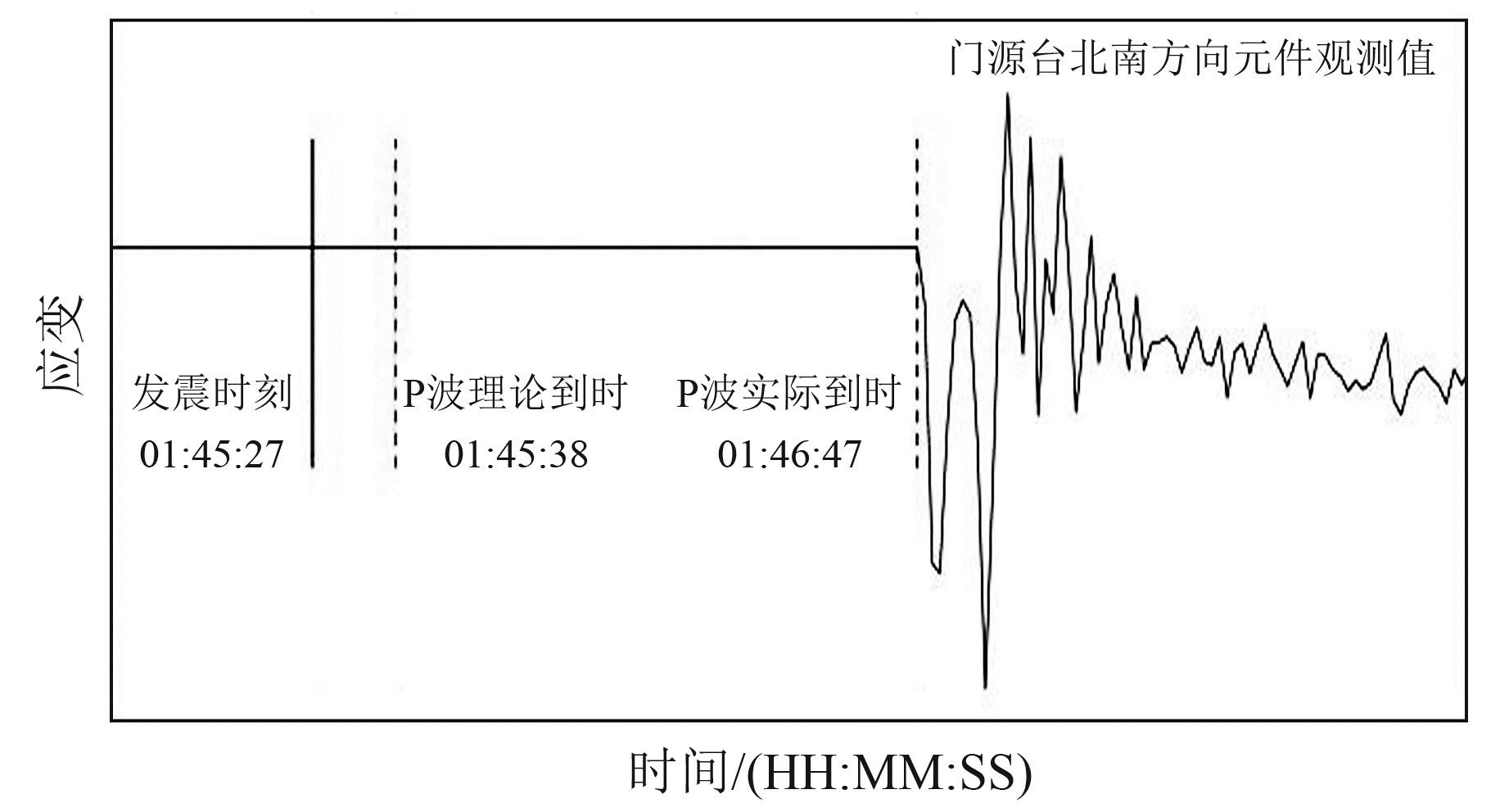
利用TauP软件[10]分别求得17个台站的P波理论走时(表 1),之后将P波实际到时与理论到时进行求差,差值即为台站的时间误差。以门源台NS向的元件观测值为例,发震时刻为01:45:27,P波的理论走时为11 s,即P波的理论到时为01:45:38,但是P波的实际到时却为01:46:47,表明门源台仪器时间滞后了69 s(图 1)。相同的方法分别应用到其余16个台站,确定仪器的误差时间(表 1),完成对仪器时间的校正。
|
|
表 1 各台站时间误差 Tab. 1 Time error of each station |
|
图 1 门源台时间校正 Fig. 1 Menyuan station time correction |
我国四分量钻孔应变仪经多年运行,仪器探头得以改进,最大的亮点就是四元件观测,即元件两两夹角为45°。四元件观测值满足关系式:
| $ S_1+S_3=S_2+S_4 $ | (1) |
式中,Si(i=1,2,3,4)为四元件的观测值,其中S1+S3和S2+S4均为观测面应变,当仪器与围岩的耦合处于理想状况时两者应相等[8]。
自洽程度决定观测数据的可靠程度。为衡量自洽程度,引入面应变相关系数r[11]:
| $ \begin{array}{*{20}{c}} {r=}\\ {\frac{\sum S_{13} S_{24}-\frac{\sum S_{13} \sum S_{24}}{N}}{\sqrt{\left(\sum S_{13}^2-\frac{\left(\sum S_{13}\right)^2}{N}\right)\left(\sum S_{24}^2-\frac{\left(\sum S_{24}\right)^2}{N}\right)}}} \end{array} $ | (2) |
式中,S13和S24分别表示S1+S3和S2+S4,N表示数据个数。r越接近1表明观测数据自洽程度越高,观测数据越可靠。
分别计算17个台站观测数据的面应变相关系数r1(表 2),可以看出,多数台站的观测数据面应变相关系数接近于1,基本符合自洽,证明完整岩石可被看作理想弹性体。数据不十分符合自洽方程时,可能是井下探头中的元件灵敏度发生了不一致的变化。例如,在将探头装入钻孔的过程中,各元件的灵敏度可能因温度等因素的变化而发生不一致的变化。对于这种变化,可以对所有元件的灵敏度变化进行相对实地标定,对观测数据进行校正,具体标定方法见文献[8]。
|
|
表 2 各台站面应变相关系数以及元件灵敏度标定系数 Tab. 2 Strain correlation coefficient of each station and calibration coefficient of element sensitivity |
上述Si(i=1,2,3,4)是钻孔应变仪4个元件直接观测的元件探头套筒内径的相对变化,即元件长度变化量与元件长度之比,因此仪器测量的并不是实际应变变化[12]。同时,仪器元件布设时往往与地理坐标轴存在夹角,为便于后续研究,本文将元件观测值换算为地理坐标轴上NS向和EW向的正应变。
平面应变状态只有3个独立分量,而四分量钻孔应变仪有4个元件,记录4个观测值。一般情况下,令
| $ \left\{\begin{array}{l} s_{13}=S_1-S_3 \\ s_{24}=S_2-S_4 \\ s_a=\left(S_1+S_3+S_1+S_3\right) / 2 \end{array}\right. $ | (3) |
将4个直接观测值转化为3个替代观测值(s13,s24,sa),来求解3个未知分量。3个未知分量的表示方法有多种,最常用的是求解ε1、ε2、φ,其中ε1为最大主应变,ε2为最小主应变,φ为最大主应变方向,其表达的物理意义最清晰,还可进一步转换为其他形式的独立分量。
已知观测值与主应变和主方向(ε1,ε2,φ)的关系为:
| $ \left\{\begin{array}{l} S_1=A\left(\varepsilon_1+\varepsilon_2\right)+B\left(\varepsilon_1-\varepsilon_2\right) \cos 2\left(\theta_1-\varphi\right) \\ S_2=A\left(\varepsilon_1+\varepsilon_2\right)-B\left(\varepsilon_1-\varepsilon_2\right) \sin 2\left(\theta_1-\varphi\right) \\ S_3=A\left(\varepsilon_1+\varepsilon_2\right)-B\left(\varepsilon_1-\varepsilon_2\right) \cos 2\left(\theta_1-\varphi\right) \\ S_4=A\left(\varepsilon_1+\varepsilon_2\right)+B\left(\varepsilon_1-\varepsilon_2\right) \sin 2\left(\theta_1-\varphi\right) \end{array}\right. $ | (4) |
式中,θ1为S1的方位角。联立式(3)和式(4)可求出主应变和主方向(ε1,ε2,φ):
| $ \left\{\begin{array}{l} \varepsilon_1=\frac{1}{4 A} s_a+\frac{1}{4 B} s_s \\ \varepsilon_2=\frac{1}{4 A} s_a-\frac{1}{4 B} s_s \\ \varphi=\frac{1}{2} \arctan \left(\frac{s_{24}}{s_{13}}\right)+\theta_1 \end{array}\right. $ | (5) |
进行钻孔应变观测的应变换算需要知道耦合系数A和B的值,其与套筒的材料和尺寸、水泥的材料和尺寸及周围岩石的性质都有复杂的关系,一般使用实地绝对标定方法确定,具体公式为:
| $ \left\{\begin{array}{l} s_a=2 A\left(\varepsilon_n+\varepsilon_e\right) \\ s_s=2 B\left(\sqrt{\left(2 \varepsilon_{n e}\right)^2+\left(\varepsilon_n-\varepsilon_e\right)^2}\right) \end{array}\right. $ | (6) |
式中,ss=
地理坐标系下平面的3个独立分量表示为εN、εE、εNE,其与ε1、ε2、φ的关系为[8]:
| $ \left\{\begin{array}{l} \varepsilon_N=\frac{\varepsilon_1+\varepsilon_2}{2}+\frac{\varepsilon_1-\varepsilon_2}{2} \cos 2 \varphi \\ \varepsilon_E=\frac{\varepsilon_1+\varepsilon_2}{2}-\frac{\varepsilon_1-\varepsilon_2}{2} \cos 2 \varphi \\ \varepsilon_{N E}=\frac{\varepsilon_1-\varepsilon_2}{2} \sin 2 \varphi \end{array}\right. $ | (7) |
根据式(7)将17个台站的四分量钻孔应变仪原始观测应变值换算为地理坐标系下的NS向正应变εN和EW向正应变εE。
1.4 滤波处理钻孔应变仪原始观测数据中通常包括长周期低频潮汐信号及一些高频干扰信号,这些信息会影响地震信号的识别,一般需要通过滤波处理将其去除[6]。经过应变换算得到的正应变数据存在同样的问题,本文设计通带频率为0.04~0.20 Hz的带通滤波器对NS向和EW向的正应变数据进行滤波处理。
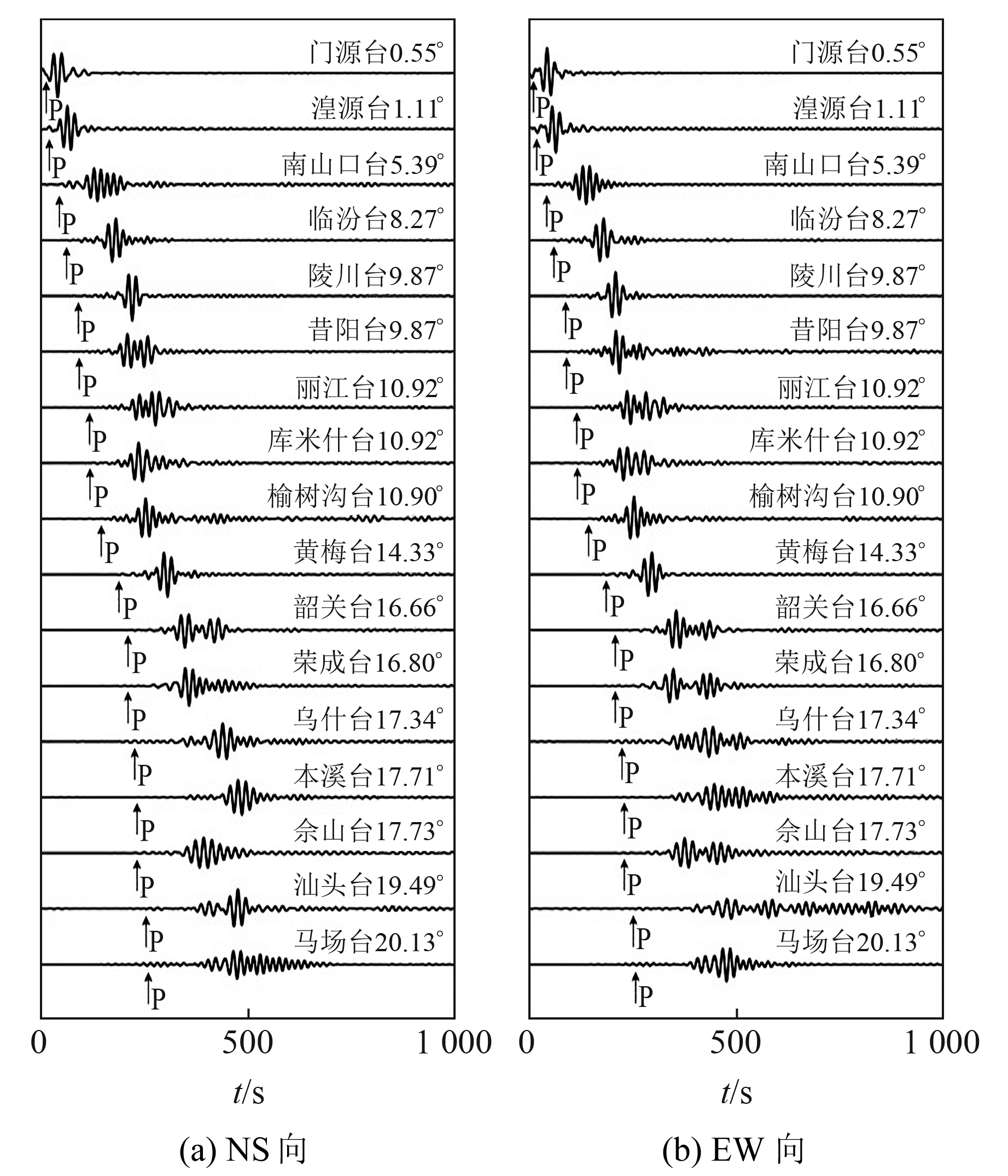
滤波处理后以门源地震发震时刻(01:45:27)为零点,时间长度截取1 000 s,按震中距大小排列,分别得到17个台站NS向和EW向的应变观测值波形(图 2),同时在图中标明P波初至时刻。
|
图 2 应变观测值 Fig. 2 Strain observations |
可以看出,NS向和EW向的观测波形中多数台站的P波初至震相清晰,符合表 1中的P波理论走时,仅有门源、湟源、汕头和马场4个台站的P波初至震相不清晰。可能是由于门源台和湟源台震中距较小,P波和S波到达时间相差不大,经滤波处理后波形叠加导致震相不清晰;而汕头台和马场台震中距较大,应变波存在衰减,经滤波处理后震相识别产生困难。但是,由于前期对观测数据进行了时间校正,P波的实际到时与理论到时一致,因此可根据理论到时对P波初至时刻进行识别。
2 同震应变模拟值计算 2.1 正演软件QSSPQSSP是由德国地学研究中心(GFZ)汪荣江教授基于Fortran编程语言编写的一款计算完整合成地震图的软件,内置具有大气、海洋、地幔、液态外核和固态内核多层结构的球对称自引力地球模型[13],可用于正演计算地震发生后地表任意位置、任意时间范围的应变、应力、速度、位移、重力等参数的同震动态变化值。
2.2 数值模拟QSSP软件由源代码文件、执行文件和参数输入文件3部分组成,正演计算理论模拟数值时需要修改参数输入文件的内容,并在执行文件中运行,具体需要修改的主要参数见表 3,其余参数可根据需求进行修改。
|
|
表 3 QSSP计算时使用的参数 Tab. 3 Parameters used in QSSP calculation |
本文参考美国地质调查局(USGS)提供的断层破裂模型参数修改参数输入文件,分别计算17个台站处的理论模拟应变值,同时为与观测数据的处理方式保持一致,将带通滤波器通带频率设置为0.04~0.2 Hz,地球模型使用AK135模型。计算得到的理论应变值为地理坐标系下的张量形式,为便于研究本文选取NS向和EW向的理论正应变值。
2.3 模拟值波形将NS向和EW向的理论正应变值截取1 000 s,按震中距排列分别得到17个台站NS向和EW向的应变模拟值波形(图 3),同时在图中标出P波初至时刻。从图中可以看出,NS向和EW向的模拟波形中大部分台站的P波初至震相清晰,P波走时符合表 1的理论走时,仅南山口台的模拟波形在发震时刻后存在波动,使P波的初至震相识别产生困难。

|
图 3 应变模拟值 Fig. 3 Strain simulations |
相较于其他震相,P波震相既容易识别,又较为单一,并且前文得到的观测波形和模拟波形基本上都清晰识别到了P波的初至震相,因此本文以初至时刻对齐的方式对观测值和模拟值的P波进行拟合。
3.1 相关系数本文使用式(8)计算相关系数ρ对波形拟合程度进行评价,其中G、M、n分别表示观测值、模拟值和数据个数,相关程度类型按相关系数大小分为4类(表 4),相关系数越接近于1表明相关程度越高,越接近于0则表明相关程度越差:
| $ \begin{array}{*{20}{c}} & \rho= \\ & \frac{\sum G M-\frac{\sum G \sum M}{n}}{\sqrt{\left(\sum G^2-\frac{\left(\sum G\right)^2}{n}\right)\left(\sum M^2-\frac{\left(\sum M\right)^2}{n}\right)}} \end{array} $ | (8) |
|
|
表 4 相关程度的类型 Tab. 4 Types of correlation degree |
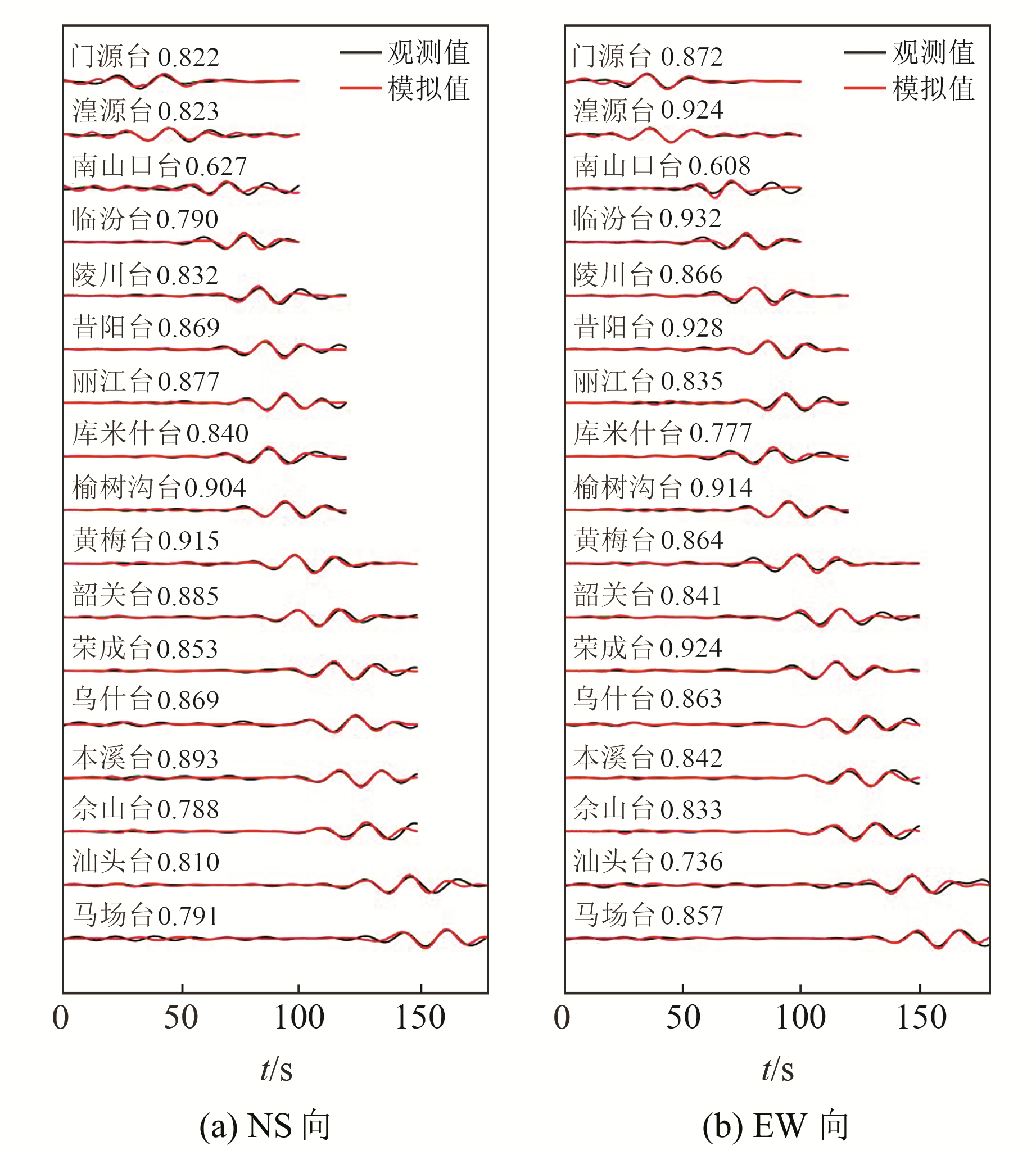
为保证截取到完整的P波波形,需要按照震中距大小选择合适的时间长度(表 5),之后以P波初至时刻为零点,按震中距从小到大的顺序对17个台站NS向和EW向的P波观测值和理论值分别进行拟合并计算其相关系数(表 6),得到二者的拟合波形,拟合相关系数标注于图 4台站名称后面。
|
|
表 5 拟合截取时间长度 Tab. 5 Fitting intercept time length |
|
|
表 6 拟合波形相关系数 Tab. 6 Fitting waveform correlation coefficient |
|
图 4 P波观测值与模拟值拟合 Fig. 4 P wave observations fitting with simulations |
从拟合结果来看,NS向有13个台站的拟合相关系数大于0.8,为高度相关,占台站总数的76.5%;有4个台站为中度相关,占台站总数的23.5%;总的相关系数平均值为0.835,达到了高度相关的标准。EW向有14个台站的拟合相关系数大于0.8,为高度相关,占台站总数的82.4%;有3个台站为中度相关,占台站总数的17.6%;总的相关系数平均值为0.842,也达到高度相关的标准。
综上所述,本文利用USGS提供的断层破裂模型参数,基于QSSP软件计算得到理论应变模拟值与实际应变观测值的P波震相吻合较好,17个台站的波形拟合程度普遍达到了高度相关。结果表明,钻孔应变观测数据可以较好地记录到地震破裂信息,理论上可以作为研究地震破裂过程的数据源。
4 结语本文以2022年门源MS6.9地震为例,将17个台站的四分量钻孔应变仪1 sps采样率的同震应变观测值经时间校正、实地相对标定、应变换算等一系列处理后,与基于USGS断层破裂模型参数通过QSSP软件计算求得的同震应变模拟值的P波进行拟合分析,得到以下结论:
1) 钻孔应变仪仪器时间的准确性直接关系到观测数据的可信度,本文对17个台站的钻孔应变仪利用P波理论走时的计算方法进行时间校正,消除时间偏差。
2) 对钻孔应变仪4个元件的灵敏度进行一致性检验,计算各元件的灵敏度标定系数。利用这个结果对观测数据进行校正,校正后观测数据的自洽程度得到显著提高,作为自洽评价标准的面应变相关系数普遍达到0.9以上。
3) 17个台站的P波观测波形与模拟波形的拟合效果较好,相关程度普遍达到了高度相关,NS向和EW向的拟合相关系数平均值分别为0.835和0.842。拟合结果表明,钻孔应变仪同震观测数据与同震模拟数据具有较好的一致性,说明钻孔应变观测数据可较好地反映地震破裂信息,具备约束地震破裂过程的潜力,进一步验证钻孔应变观测数据可用于地震破裂过程的研究。
| [1] |
李海亮, 李宏. 钻孔应变观测现状与展望[J]. 地质学报, 2010, 84(6): 895-900 (Li Hailiang, Li Hong. Status and Developments of Borehole Strain Observations in China[J]. Acta Geologica Sinica, 2010, 84(6): 895-900)
(  0) 0) |
| [2] |
Sacks I S, Suyehiro S, Evertson D W. Sacks-Evertson Strainmeter, Its Installation in Japan and Some Preliminary Results Concerning Strain Steps[J]. Proceedings of the Japan Academy, 1971, 47(9): 707-712 DOI:10.2183/pjab1945.47.707
(  0) 0) |
| [3] |
Farghal N, Barbour A, Langbein J. The Potential of Using Dynamic Strains in Earthquake Early Warning Applications[J]. Seismological Research Letters, 2020, 91(5): 2 817-2 827 DOI:10.1785/0220190385
(  0) 0) |
| [4] |
李富珍, 张怀, 唐磊, 等. 基于钻孔应变地震波记录确定地震面波应变震级[J]. 地球物理学报, 2021, 64(5): 1 620-1 631 (Li Fuzhen, Zhang Huai, Tang Lei, et al. Determination of Seismic Surface Wave Strain Magnitude Based on Borehole Strain Seismic Wave Records[J]. Chinese Journal of Geophysics, 2021, 64(5): 1 620-1 631)
(  0) 0) |
| [5] |
石耀霖, 尹迪, 任天翔, 等. 首次直接观测到与理论预测一致的同震静态应力偏量变化: 2016-04-07山西原平ML4.7地震的钻孔应变观测[J]. 地球物理学报, 2016, 64(6): 1 937-1 948 (Shi Yaolin, Yin Di, Ren Tianxiang, et al. The Variation of Coseismic Static Stress Deviation Consistent with Theoretical Prediction was Observed for the First Time—Observation of Borehole Strain of the Yuanping ML4.7 Earthquake in Shanxi on April 7, 2016[J]. Chinese Journal of Geophysics, 2016, 64(6): 1 937-1 948)
(  0) 0) |
| [6] |
范智旎, 万永革. 应变仪记录的印尼苏门答腊海域7.8级地震的同震信号研究[J]. 大地测量与地球动力学, 2020, 40(8): 849-853 (Fan Zhini, Wan Yongge. Study on Co-Seismic Signal of the M7.8 Earthquake in Sumatra, Indonesia, Recorded by Strainmeter[J]. Journal of Geodesy and Geodynamics, 2020, 40(8): 849-853)
(  0) 0) |
| [7] |
王洵, 王卫民, 赵俊猛, 等. InSAR、波形资料和GPS联合反演2015年皮山地震震源破裂过程[J]. 中国科学: 地球科学, 2019, 49(2): 383-397 (Wang Xun, Wang Weimin, Zhao Junmeng, et al. Rupture Process of the 2015 Pishan Earthquake from Joint Inversion of InSAR, Teleseismic Data and GPS[J]. Scientia Sinica(Terrae), 2019, 49(2): 383-397)
(  0) 0) |
| [8] |
邱泽华. 钻孔应变观测理论和应用[M]. 北京: 地震出版社, 2017 (Qiu Zehua. Theory and Application of Borehole Strain Observation[M]. Beijing: Seismological Press, 2017)
(  0) 0) |
| [9] |
龚正, 李海兵, 荆燕, 等. 2016年M6.2呼图壁地震发震构造及其对天山构造带隆升的启示: 来自中近场钻孔应变观测的证据[J]. 地球物理学报, 2020, 63(4): 1 386-1 402 (Gong Zheng, Li Haibing, Jing Yan, et al. Seismogenic Structure of the 2016 M6.2 Hutubi Earthquake and Its Implication for the Uplift Process in Tian Shan: Evidence from Borehole Strainmeters in the near to Intermediate Field[J]. Chinese Journal of Geophysics, 2020, 63(4): 1 386-1 402)
(  0) 0) |
| [10] |
Crotwell H P, Owens T J, Ritsema J. The TauP Toolkit: Flexible Seismic Travel-Time and Ray-Path Utilities[J]. Seismological Research Letters, 1999, 70(2): 154-160 DOI:10.1785/gssrl.70.2.154
(  0) 0) |
| [11] |
唐磊, 邱泽华, 樊俊屹, 等. 不同采样率下四分量钻孔应变观测同震变化特征[J]. 大地测量与地球动力学, 2022, 42(11): 1 196-1 201 (Tang Lei, Qiu Zehua, Fan Junyi, et al. Characteristic Analysis of Coseismic Variation of 4-Component Borehole Strain Observation with Different Sampling Rates[J]. Journal of Geodesy and Geodynamics, 2022, 42(11): 1 196-1 201)
(  0) 0) |
| [12] |
邱泽华, 阚宝祥, 唐磊. 四分量钻孔应变观测资料的换算和使用[J]. 地震, 2009, 29(4): 83-89 (Qiu Zehua, Kan Baoxiang, Tang Lei. Conversion and Application of 4-Component Borehole Strainmeter Data[J]. Earthquake, 2009, 29(4): 83-89)
(  0) 0) |
| [13] |
Wang R J, Heimann S, Zhang Y, et al. Complete Synthetic Seismograms Based on a Spherical Self-Gravitating Earth Model with an Atmosphere-Ocean-Mantle-Core Structure[J]. Geophysical Journal International, 2017, 210(3): 1 739-1 764 DOI:10.1093/gji/ggx259
(  0) 0) |
2. Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China
 2024, Vol. 44
2024, Vol. 44


