2. 中国地质大学(武汉)地质探测与评估教育部重点实验室,武汉市鲁磨路388号,430074
准确掌握地下目标分布信息可为合理安全规划利用地下空间、监测预警地质灾害、强化地下国防工程探测与防护能力、消除边境安全隐患等提供技术支撑[1-2]。确定目标的空间位置和形状是地下目标探测的核心任务,基于线性反演方法容易陷入局部最优解的问题[3-5],而属于非线性概率反演方法的贝叶斯推断理论上能得到全局最优解[6-8],近年来在各领域都得到了广泛应用[9]。
基于此,本文针对地下目标形状和位置信息均未知的情况,区分面测量和少量测线测量两种典型应用场景,通过模拟实验对贝叶斯推断探测地下目标的可行性和有效性进行分析。
1 研究方法 1.1 规则形体重力场正演空洞、隧道、地下建筑等一般具有规则形体,可用球体、长方体、水平圆柱体等近似,这样能有效简化问题,且能通过简单规则形体的组合叠加研究更复杂的地下目标[10]。因此,本文以水平长方体为研究对象,模拟分析地下目标引起的重力和重力梯度异常。
假设在空间直角坐标系下观测点的坐标为(xp,yp,zp), 长方体的范围为x1≤x≤x2,y1≤y≤y2,z1≤z≤z2,z轴向下为正,则相应的计算公式[11]为:
| $ \begin{aligned} g_z= & G \Delta \rho[x \ln (y+r)+y \ln (x+r)- \\ & \left.z \arctan \left(\frac{x y}{z r}\right)\right] \left.\left|\begin{array}{l} x_b \\ x_a \end{array}\right| \begin{array}{l} y_b \\ y_a \end{array} \right| \begin{array}{l} z_b \\ z_a \end{array} \end{aligned} $ | (1) |
| $ \left.g_{z z}=G \Delta \rho \arctan \left(\frac{x y}{z r}\right)\left|\begin{array}{l} x_b \\ x_a \end{array}\right| \begin{gathered} y_b \\ y_a \end{gathered} \right| \begin{aligned} & z_b \\ & z_a \end{aligned} $ | (2) |
令ta、tb(t=x、y、z)代表积分上限和下限,则式(1)和式(2)中各参量的积分上、下限可定义为ta=t1-tp、tb=t2-tp。当目标体的走向长度比截面的尺度和埋藏深度大得多,且观测剖面位于目标长轴中部时,可将其视为二度体,无需考虑长轴方向的重力场变化,此时可对式(1)和式(2)进行进一步简化[10]。
如果局部测量坐标系xoy与长方体坐标系uov不重合,即目标体的走向与测线存在如图 1所示的锐角α(逆时针为正)时,应先进行坐标旋转,然后再进行重力和重力梯度计算。水平旋转矩阵定义如下:
| $ \boldsymbol{R}=\left[\begin{array}{cc} \cos \beta & \sin \beta \\ -\sin \beta & \cos \beta \end{array}\right] $ | (3) |
| $ \left[\begin{array}{l} x \\ y \end{array}\right]=\boldsymbol{R}(90-\alpha)\left[\begin{array}{l} u \\ v \end{array}\right] $ | (4) |

|
图 1 测量坐标系与长方体坐标系示意图 Fig. 1 Schematic diagram of measurement coordinate andcuboid coordinate |
贝叶斯公式的密度函数形式定义为[12]:
| $ \pi(\theta \mid \boldsymbol{q})=\frac{f(\boldsymbol{q} \mid \theta) \pi(\theta)}{\int_\mathit{Θ} f(\boldsymbol{q} \mid \theta) \pi(\theta) \mathrm{d} \theta} $ | (5) |
式中,π(θ)为未知参数θ的先验分布,即在抽取样本Q之前对θ的认识,π(θ | q)为θ的后验分布,即给定样本Q=q条件下θ的条件分布,分母称为证据或Q的边缘密度。
为了显式地描述推断过程中依赖的模型M,也可将上式写为:
| $ \begin{gathered} \pi(\theta \mid \boldsymbol{q}, M)=\frac{f(\boldsymbol{q} \mid \theta, M) f(\theta \mid M)}{f(\boldsymbol{q} \mid M)}= \\ \frac{f(\boldsymbol{q} \mid \theta, M) f(\theta \mid M)}{\int_\mathit{Θ} f(\boldsymbol{q} \mid \theta, M) f(\theta \mid M) \mathrm{d} \theta_m} \end{gathered} $ | (6) |
为计算出证据f(q | M),需要边缘化(通过离散求和或积分)所有可能的f(θ | M),即根据给定模型边缘化所有θ的先验[13]。
1.2.2 似然函数测线上第i个点的观测值qi可表示为:
| $ q_i=s_i+n_b+n_{\text {inst }} $ | (7) |
式中,si为目标产生的信号,可由式(1)或式(2)得到,nb为背景场噪声,ninst为测量设备产生的噪声。观测数据与正演模型之间的差异(噪声)序列可视为服从均值为0,协方差为Σ的正态分布,其中协方差Σ=Φb+Φinst由背景场噪声协方差和设备噪声协方差组成。在此基础上,将观测序列的似然函数表示为:
| $ \begin{gathered} p(\boldsymbol{q} \mid \theta, M)=\frac{1}{\sqrt{(2 \pi)^k|\mathit{\Sigma}|}} \\ \exp \left(-\frac{1}{2}(\boldsymbol{q}-\boldsymbol{s})^{\mathrm{T}} \mathit{\Sigma}^{-1}(\boldsymbol{q}-\boldsymbol{s})\right) \end{gathered} $ | (8) |
有了总体信息模型和样本数据,只要获取先验信息,就可根据式(8)的贝叶斯公式推断参数的后验分布。
1.2.3 先验信息如果仅知道地下目标位于测量区域内,且目标呈水平长方体形状,则长方体的形状参数(长、宽、高)、位置信息(中心坐标(x0,y0,z0)和目标深度d、走向α及引起信号异常的剩余密度Δρ均为未知参数。在进行贝叶斯推断之前需要确定这些未知参数的先验信息,具体内容将在实验部分展开介绍。至此,确定了总体模型、似然函数和先验信息,之后可以进行贝叶斯推断,推断过程见图 2。

|
图 2 贝叶斯推断基本流程 Fig. 2 Flowchart of Bayesian inference |
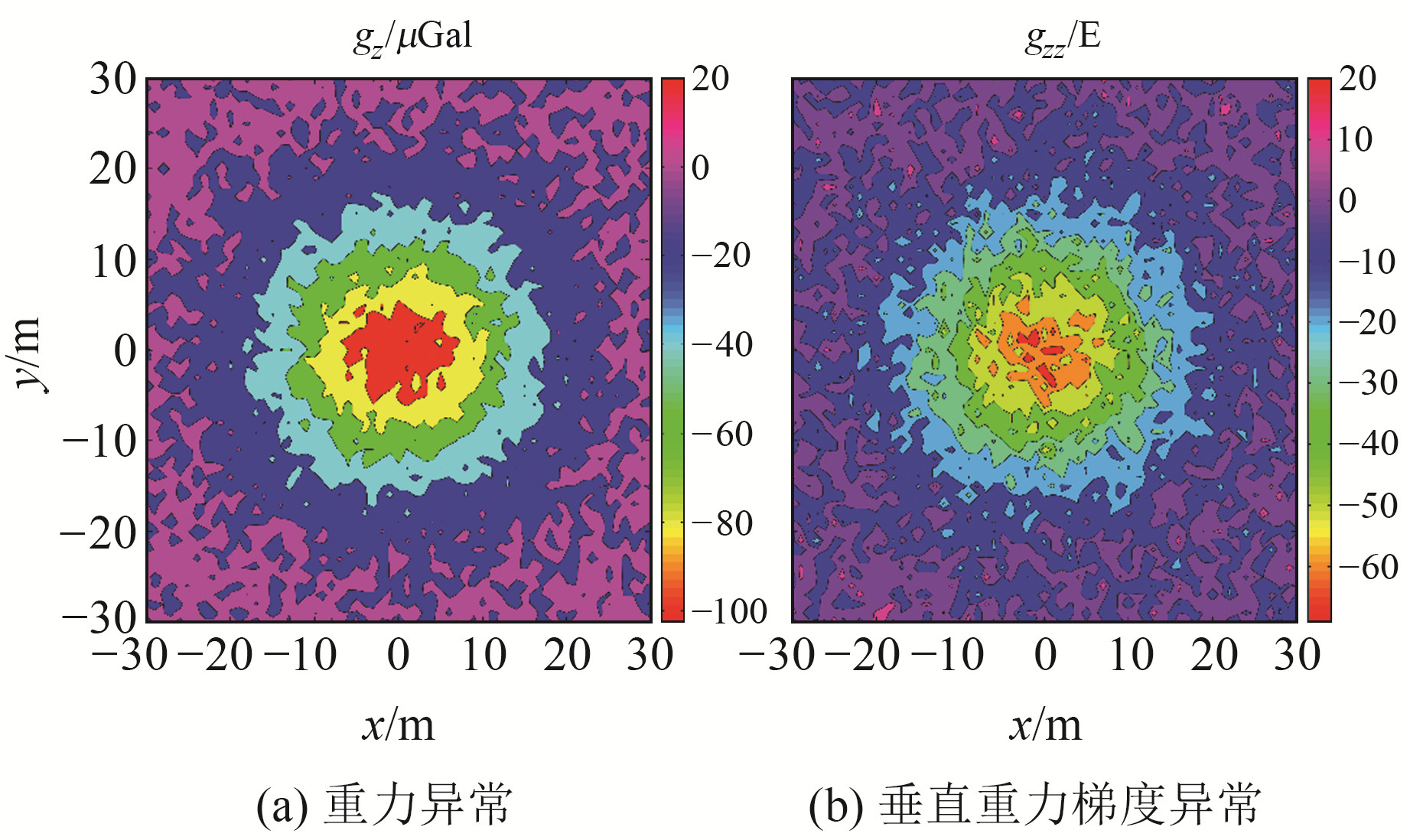
为验证本文方法的可行性,首先用1个20 m×15 m×5 m、顶部位于地面以下15 m、剩余密度为-2 300 kg/m3的长方体模拟地下隧道,同时以长方体为中心在60 m×60 m范围内分别按3 m、6 m、9 m间距进行地面重力、垂直重力梯度测量。假设该区域内无明显的地质干扰和地形起伏,对观测数据分别加入不同程度的高斯白噪声,然后验证探测效果。图 3(a)为加入6 μGal白噪声的重力异常分布,图 3(b)为加入6 E白噪声的垂直重力梯度异常分布。
|
图 3 模拟的区域重力异常和垂直重力梯度异常 Fig. 3 Simulated gravity anomalies and vertical gravity gradients anomalies |
根据上节内容,进行贝叶斯推断前需要确定所有未知参数的先验信息。考虑到长方体的长(l)、宽(w)、高(h)和埋深(d)必须为正值,因此可假设其先验服从伽马分布;长方体中心的水平坐标(x0,y0)不可能位于测区以外且取值可正可负,因此设定其服从正态分布;地下空洞一般因质量亏空才产生异常信号,因此剩余密度的先验可设定为服从均值为负、具有一定标准差的正态分布。表 1详细列举了各参数的定义及先验信息,相应的概率密度分布见图 4。
|
|
表 1 未知参数的定义及先验分布 Tab. 1 Definition and prior distribution function of unknown parameters |

|
图 4 未知参数的先验概率密度分布 Fig. 4 Prior probability density distributions for unknown parameters |
结合表 1的先验信息及图 3的观测数据,在Python中调用PYMC3库函数即可实现贝叶斯推断过程。对采样过程进行收敛性和相关性分析后,最终得到如表 2所示的后验统计信息。
|
|
表 2 根据区域重力/垂直重力梯度数据的贝叶斯推断结果 Tab. 2 Bayesian inference results based on regional gravity/vertical gravity gradient data |
以长度参数为例,从表 2中可以看出,即使以3 m间距、噪声标准差仅为2 μGal的精度进行微重力测量, 反演结果的94% HDI(相应的上下界分别对应表中3% HDI和97% HDI)位于均值为4.1的概率区间(0.1, 9.4)内,概率取值区间不仅分散,且与真值的偏差很大。如果使用9 m间距、噪声标准差为6 E的垂直重力梯度测量,其反演结果的94%概率区间为(18.5, 20.9),94% HDI的均值为19.7 m,概率取值区间不仅相对集中,结果也更接近真值。结合其他参数的反演结果可以看出,微重力反演浅源目标的效果远不如垂直重力梯度。这是因为该目标引起的重力异常信号最大量级也只有百μGal级,接近商用重力仪的精度极限,很容易受外界噪声的干扰;而相应的地面垂直重力梯度异常信号接近100 E,即使加入标准差为6 E的噪声,仍然具有很高的信噪比。另外,从表 2的反演结果可以看出,减小测点间距进行加密测量并没有使反演结果得到明显改善,但测点间距过大时,如采用12 m的测量间距,就会出现反演结果发散的现象(文中未列出实验结果)。
总体来看,水平位置、剩余密度及长、宽等参数的反演效果要明显优于深度、高度等垂向参数。图 5以表 2中9 m测量间距、6 E噪声的结果为例直观地反映了这种差异,其中水平位置、长、宽等参数的75% HDI与真值相差不足1 m;而深度、高度等参数的75% HDI与真值最大相差5 m,这是因为重力/重力梯度数据本身就没有垂向分辨能力,不管真实深度如何,反演结果总是趋于近地表。熊盛青[14]将这一现象称为“趋肤效应”或模型“上漂”,下一步将尝试结合深度加权技术克服该现象。

|
图 5 模型参数的贝叶斯后验概率分布 Fig. 5 Bayesian posterior probability distributions for model parameters |
为验证先验信息对推断结果的影响,将表 1中γ分布函数的参数调整为(3,1)或(4,0.5),并重复上述实验。反演结果与表 2无明显差异,说明先验信息取值范围具有合理性。因此,贝叶斯推断能合理估计探测目标中的未知参数,地面重力梯度观测比重力异常探测更具探测优势。
2.2 基于少量测线重力梯度数据的目标探测实验在一些特殊应用领域,受地形地物特征或观测条件的限制,往往无法进行大面积区域测量,甚至无法进行地面测量。因此,有必要研究低空平台少量测线数据探测地下目标的可行性。针对这一应用场景,顾及上一实验中垂直重力梯度探测效果明显优于微重力的结果,本文仅利用重力梯度数据分析贝叶斯推断的应用效果。
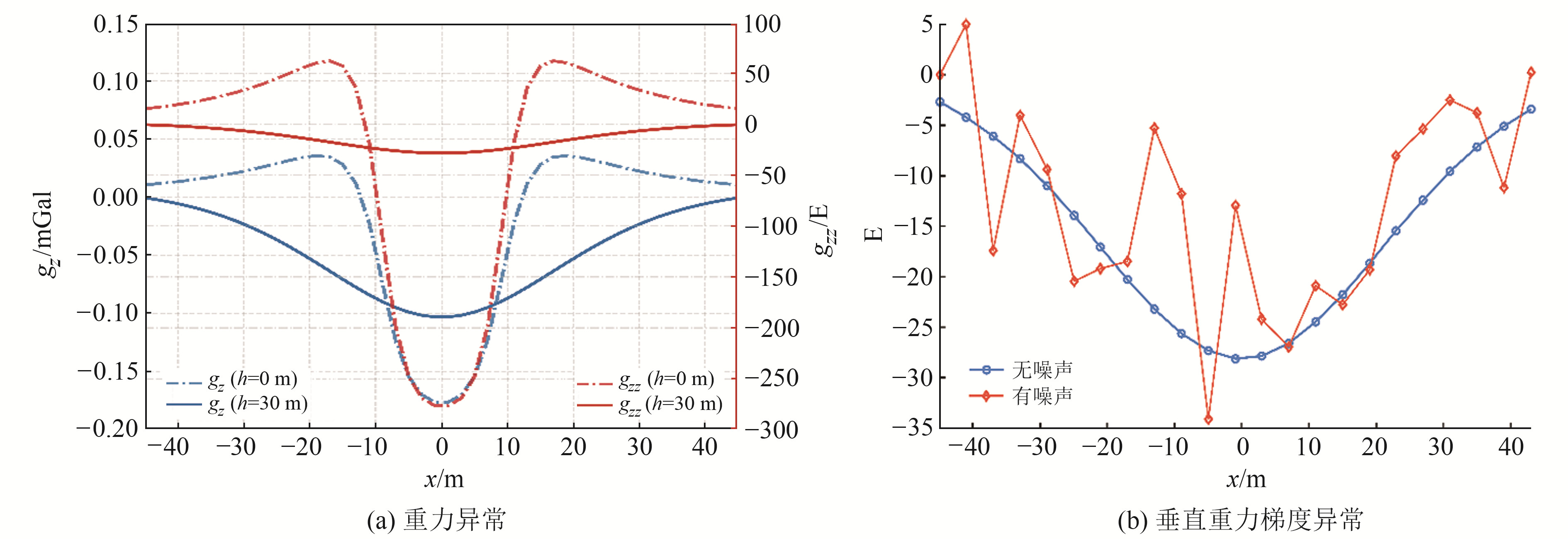
Romaides等[15]曾对一处地下地铁停车场进行地面微重力测量,该地下设施长150 m、宽18.3 m、高8.5 m,顶部距地表 3.7 m。因剩余密度未知,本文取值为-1 900 kg/m3,并在目标中部生成2条与目标体长轴呈35°方向的测线(图 1)。测线长90 m,以长方体长轴为中心,测点间距分别设为2 m、4 m、8 m和12 m,并加入不同程度的白噪声(表 3)。图 6(a)为地面(虚线)及30 m高度上(实线)重力和垂直重力梯度正演结果。尽管地面重力异常(蓝色虚线)量级明显低于文献[15]中的实测值,但较小的剩余密度更有助于验证本文方法的可行性。图 6(b)为30 m高度上的重力梯度正演结果(蓝色曲线)及加入6 E白噪声的结果(红色曲线)。
|
|
表 3 少量测线垂直重力梯度数据的贝叶斯推断结果 Tab. 3 Bayesian inference results based on a few vertical gravity gradient survey lines |
|
图 6 不同高度上的重力异常和重力梯度测线数据 Fig. 6 Survey line data of gravityanomalies and gravity gradient anomalies at different altitudes |
若已知该目标呈长方体状,且可视为水平无限长二度体,那么在目标探测时就无需考虑长轴方向的中心坐标及长度,其余未知参数的先验信息同表 2。此外,因目标体的走向未知,需要增加水平走向参数α,根据定义,其取值在(-90°~90°),可将其先验分布设定为均匀分布U(-90°,90°)。
推断结果如表 3所示,可以看出,只有1条测线时,尽管噪声的标准差达到正演信号最大值的20%左右,但除水平走向α之外,其余参数的真值基本都位于后验的94% HDI内,但参数概率取值区间较上节较为分散,结果不一定真实可靠,加密测量也未能改善推断结果。虽然不能从1条测线的数据推断出水平走向角,但不难发现,94% HDI的上下界(分别对应97% HDI和3% HDI)大致确定了目标走向的可能取值β0。因此,根据1条测线的推断结果,基本能够确定走向角介于±β0之间。
为推断走向角,使用2条测线的数据重复上一实验。从表 3中可以看出,2条测线的观测数据能够很好地推断出包括走向角在内的所有参数信息。若进一步将表 3中剩余密度的先验分布均值设置为-1 600 kg/m3或-2 300 kg/m3,推断结果并未产生明显的变化。由此说明,在信噪比较大的情况下,即使地下目标的剩余密度未知,也可在反演中作出相对合理的估计。
以表 3中2条测线、间距4 m、噪声标准差为3 E的后验结果绘制出参数的边缘分布及y0、z0的联合概率密度分布(图 7)。结合表 3中94% HDI结果可以看出,图 7中各参数的75% HDI和概率区间均值的可靠性更高。因此,在具体应用中可根据需要设定不同的HDI参考值。

|
图 7 模型参数的贝叶斯后验概率分布 Fig. 7 Bayesian posterior probability distributions for model parameters |
以上实验结果表明,即使只有1条与目标相交的测线,也能对地下目标的位置和形状参数作出相对保守、合理的估计;当测线与目标走向不垂直时,至少需要2条与目标相交的测线才能确定地下目标的走向。
3 结语本文通过正演分析计算规则形状的地下目标产生的重力/重力梯度异常信号,进而验证贝叶斯推断用于地下目标探测的可行性和有效性。实验结果表明:
1) 地面垂直重力梯度测量较微重力测量具有更高的信噪比,使用贝叶斯推断能对地下目标的位置、形状、剩余密度等参数作出合理估计。结合测区的坐标范围合理设定目标位置、形状等参数的先验信息,可使反演结果更趋于真值。
2) 对于未知走向的地下目标,至少需要2条与目标相交的测线才能确定目标的走向参数。
本文研究初步验证了贝叶斯推断用于地下目标探测的可行性,但对于实验中出现的深度参数反演结果“上漂”的问题尚未解决。尽管通过模拟实验分析了地下目标在一定高度上的重力场信号及其贝叶斯推断结果,但针对复杂背景场相关噪声及地形起伏影响下地下目标信号的探测识别仍有待进一步研究。
| [1] |
洪开荣. 我国隧道及地下工程发展现状与展望[J]. 隧道建设, 2015, 35(2): 95-107 (Hong Kairong. State-of-Art and Prospect of Tunnels and Underground Works in China[J]. Tunnel Construction, 2015, 35(2): 95-107)
(  0) 0) |
| [2] |
陈家运, 孟醒, 谢伟, 等. 地下工程地球物理探测技术进展与启示[J]. 防护工程, 2022, 44(3): 70-78 (Chen Jiayun, Meng Xing, Xie Wei, et al. Progress and Enlightenment of Underground Engineering Geophysical Survey Technologies[J]. Protective Engineering, 2022, 44(3): 70-78)
(  0) 0) |
| [3] |
Jekeli C, Abt T L. The Statistical Performance of the Matched Filter for Anomaly Detection Using Gravity Gradients[R]. Ohio Stote University, Ohio, 2010
(  0) 0) |
| [4] |
Lockerbie N A. The Location of Subterranean Voids Using Tensor Gravity Gradiometry[J]. Classical and Quantum Gravity, 2014, 31(6)
(  0) 0) |
| [5] |
McKenna J R, Rim H, Li Y G. Feasibility and Limitations of Void Detection Using Gravity Gradiometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 881-891 DOI:10.1109/TGRS.2015.2468731
(  0) 0) |
| [6] |
Brown G. Bayesian Mass Anomaly Estimation with Measurements of Gravity[C]. 2nd IET International Conference on Intelligent Signal Processing, London, 2015
(  0) 0) |
| [7] |
Brown G, Ridley K, Rodgers A, et al. Bayesian Signal Processing Techniques for the Detection of Highly Localised Gravity Anomalies Using Quantum Interferometry Technology[C]. Emerging Imaging and Sensing Technologies, Edinburgh, 2016
(  0) 0) |
| [8] |
Stray B, Lamb A, Kaushik A, et al. Quantum Sensing for Gravity Cartography[J]. Nature, 2022, 602(7 898): 590-594
(  0) 0) |
| [9] |
蒋星达, 张伟, 杨辉. 地球物理反演问题中的贝叶斯方法研究[J]. 地球与行星物理论评, 2022, 53(2): 159-171 (Jiang Xingda, Zhang Wei, Yang Hui. The Research on Bayesian Inference for Geophysical Inversion[J]. Reviews of Geophysics and Planetary Physics, 2022, 53(2): 159-171)
(  0) 0) |
| [10] |
曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005 (Zeng Hualin. Gravity Field and Gravity Exploration[M]. Beijing: Geological Publishing House, 2005)
(  0) 0) |
| [11] |
Nagy D, Papp G, Benedek J. The Gravitational Potential and Its Derivatives for the Prism[J]. Journal of Geodesy, 2000, 74(7-8): 552-560
(  0) 0) |
| [12] |
韦来生, 张伟平. 贝叶斯分析[M]. 合肥: 中国科学技术大学出版社, 2021 (Wei Laisheng, Zhang Weiping. Bayesian Analysis[M]. Hefei: University of Science and Technology of China Press, 2021)
(  0) 0) |
| [13] |
Martin O. Bayesian Analysis with Python[M]. Birmingham: Packt Publishing, 2016
(  0) 0) |
| [14] |
熊盛青. 航空地球物理综合探测理论技术方法装备应用[M]. 北京: 地质出版社, 2018 (Xiong Shengqing. Application of Theory, Technology, Method and Equipment of Aviation Geophysical Comprehensive Detection[M]. Beijing: Geological Publishing House, 2018)
(  0) 0) |
| [15] |
Romaides A J, Battis J C, Sands R W, et al. A Comparison of Gravimetric Techniques for Measuring Subsurface Void Signals[J]. Journal of Physics D: Applied Physics, 2001, 34(3): 433-443
(  0) 0) |
2. Key Laboratory of Geological Survey and Evaluation of Ministry of Education, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China
 2024, Vol. 44
2024, Vol. 44

