合理地利用先验约束信息可以提高单传感器系统和多传感器系统的导航定位服务精度及可靠性。目前，将约束信息纳入到卡尔曼滤波中来处理单传感器导航数据的研究较多^[1]，而在多传感器导航系统中加入先验状态约束信息的研究较少。相较于单传感器系统，多传感器系统的观测量明显增多，但不同传感器的定位原理不同，受干扰的情形也不同。如在由捷联惯导(strapdown inertial navigation system，SINS)、GNSS和里程计(odometer，ODO)组成的SINS/GNSS/ODO组合导航系统^[2]中，GNSS信号易受高楼、树木等遮挡^[3]，车载体侧滑、滑行等现象易导致ODO的数据无效^[4]。此外，即便在所有传感器都正常工作的情况下，仍有必要考虑约束信息，因为约束通常是一个硬性界限，是必须满足的条件。

本文基于对传统联邦卡尔曼滤波算法(federated Kalman filter，FKF)^[5]的研究，将状态约束下的卡尔曼滤波扩展到联邦滤波中，提出状态约束下的联邦滤波(federated filtering with state constraints，CON-FKF)算法。另外，针对载体处于复杂环境时传感器可能出现故障或数据异常的情形，本文还对状态约束下的联邦滤波进行了改进。首先，在各个子滤波器中加入Huber抗差方法^[6]，以抵制观测异常对导航精度的影响；其次，在信息分配阶段加入基于马氏距离的自适应信息分配因子^[7-8]，得到一种状态约束下的自适应抗差联邦滤波算法(a robust adaptive federated filtering algorithm with state constraints，CON-RAFKF)，以进一步减小子滤波器的不准确估计对全局估计的影响；最后，基于SINS/GNSS/ODO组合导航系统，利用仿真实验验证本文算法的有效性。

1 SINS/GNSS/ODO组合导航数学模型 1.1 状态方程

在多传感器组合导航中，基于SINS误差方程建立状态方程，其线性状态方程可表示为^[9]：

$ \boldsymbol{X}_k=\mathit{\boldsymbol{\varPhi}}_k \boldsymbol{X}_{k-1}+\boldsymbol{w}_k $

(1)

式中，$\boldsymbol{X}_k=\left[\delta \boldsymbol{\psi}, \delta \boldsymbol{v}, \delta \boldsymbol{p}, b_\omega, b_f\right]^{\mathrm{T}}$为15维状态误差向量，δψ、δv、δp分别为姿态误差、速度误差和位置误差，b_ω、b_f分别为陀螺零偏和加速度计零偏，可被建模为随机常数^[10]；Φ_k为系统状态转移矩阵；w_k为状态过程噪声向量，其协方差矩阵为Σ_wk。

1.2 观测方程

1) GNSS/SINS观测方程。GNSS/SINS的观测值为GNSS输出的位置与SINS计算的位置之差，观测方程为^[10]：

$ \boldsymbol{Z}_{1 k}=\boldsymbol{P}_{\mathrm{GNSS}}-\boldsymbol{P}_{\mathrm{SINS}}=\boldsymbol{H}_{1 k} \boldsymbol{X}_k+\boldsymbol{\tau}_{1 k} $

(2)

式中，Z_1k为k时刻滤波位置观测值；P_GNSS为GNSS位置观测值；P_SINS为SINS位置计算值；H_1k为观测矩阵；τ_1k为观测噪声，满足高斯白噪声特性，其协方差矩阵为R_1k。

2) ODO/SINS观测方程。ODO/SINS的观测值为ODO输出的速度与SINS计算的速度之差，观测方程为^[2]：

$ \boldsymbol{Z}_{2 k}=\boldsymbol{V}_{\text {ODO }}-\boldsymbol{V}_{\mathrm{SINS}}=\boldsymbol{H}_{2 k} \boldsymbol{X}_k+\boldsymbol{\tau}_{2 k} $

(3)

式中，Z_2k为k时刻滤波速度观测值；V_ODO为ODO速度观测值；V_SINS为SINS速度计算值；H_2k为观测矩阵；τ_2k为观测噪声，满足高斯白噪声特性，其协方差矩阵为R_2k。

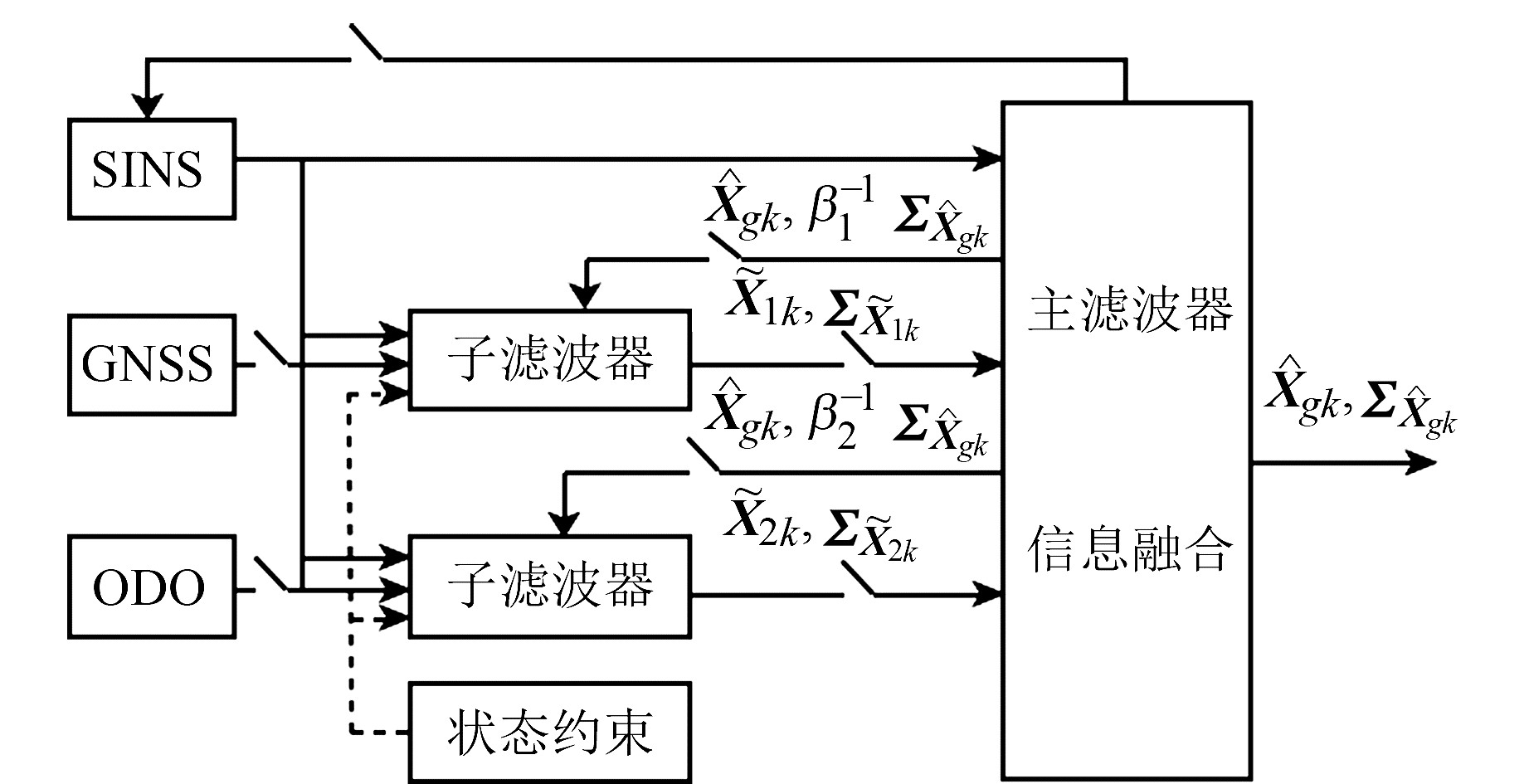
2 CON-FKF算法

CON-FKF算法具有2层结构。在第1层中，SINS分别与GNSS和ODO组合，并通过并行的方式获得状态约束下SINS/GNSS和SINS/ODO的局部状态估计值；在第2层中，将各个子滤波器的状态估计进行融合，获得SINS/GNSS/ODO组合导航系统的全局状态估计。算法结构如图 1所示。

2.1 信息融合和信息分配过程

如图 1所示，$\hat{\boldsymbol{X}}_{g k}$、$\mathit{\boldsymbol{\varSigma}}_{\hat{\boldsymbol{x}}_{g k}}$表示全局状态估计值和相应的协方差矩阵；$\widetilde{\boldsymbol{X}}_{i k}$、$\mathit{\boldsymbol{\varSigma}}_{\tilde{\boldsymbol{X}}_{i k}}$表示状态约束下第i个子滤波器的状态估计值和相应的协方差矩阵。设全局估计的权矩阵和子滤波器估计的权矩阵分别为$\boldsymbol{P}_{\hat{\boldsymbol{X}}_{g k}}=\mathit{\boldsymbol{\varSigma}}_{\hat{\boldsymbol{X}}_{g k}}^{-1}$、$\boldsymbol{P}_{\tilde{\boldsymbol{X}}_{i k}}=\mathit{\boldsymbol{\varSigma}}_{\tilde{\boldsymbol{X}}_{i k}}^{-1}$，则FKF的全局状态估计值和权矩阵^[2]为：

$ \boldsymbol{P}_{\hat{\boldsymbol{X}}_{g k}}=\sum\limits_{i=1}^r \boldsymbol{P}_{\hat{\boldsymbol{X}}_{i k}} $

(4)

$ \hat{\boldsymbol{X}}_{g k}=\mathit{\boldsymbol{\varSigma}}_{\tilde{x}_{i k}} \sum\limits_{i=1}^r \boldsymbol{P}_{\tilde{\boldsymbol{X}}_{i k}} \widetilde{\boldsymbol{X}}_{i k} $

(5)

式中，r=2为子滤波器的个数。

根据信息守恒原理，将全局估计值$\hat{\boldsymbol{X}}_{g k}$和权矩阵$\boldsymbol{P}_{\hat{\boldsymbol{X}}_{g k}}$通过信息分配因子β_i分配到子滤波器^{[2, 10]}：

$ \widetilde{\boldsymbol{X}}_{i k}=\hat{\boldsymbol{X}}_{g k} $

(6)

$ \boldsymbol{P}_{\tilde{\boldsymbol{X}}_{i k}}=\beta_i \hat{\boldsymbol{P}}_{g k} $

(7)

$ \mathit{\boldsymbol{\varSigma}}_{\boldsymbol{w}_{i k}}=1 / \beta_i \mathit{\boldsymbol{\varSigma}}_{\boldsymbol{w}_{g k}} $

(8)

$ \sum\limits_{i=1}^r \beta_i=1 $

(9)

式中，Σ_wgk、Σ_wik分别为主滤波器和第i个子滤波器的状态噪声协方差矩阵。

2.2 子滤波器状态估计

在SINS/GNSS/ODO组合导航系统中，2个子滤波器的状态方程与主滤波器的状态方程均如式(1)所示，而第i个子滤波器的观测方程可以统一表达为：

$ \boldsymbol{Z}_{i k}=\boldsymbol{H}_{i k} \boldsymbol{X}_k+\boldsymbol{\tau}_{i k} $

(10)

式中，Z_ik为第i个子滤波器的观测量；H_ik为观测矩阵；τ_ik为第i个子滤波器的观测噪声，其协方差矩阵为Σ_ik，i=1, 2。则各子滤波器的时间更新和观测更新为：

$ \overline{\boldsymbol{X}}_{i k}=\mathit{\boldsymbol{\varPhi}}_k \tilde{\boldsymbol{X}}_{i k-1} $

(11)

$ \mathit{\boldsymbol{\varSigma}}_{\bar{\boldsymbol{X}}_{i k}}=\mathit{\boldsymbol{\varPhi}}_{i k} \mathit{\boldsymbol{\varSigma}}_{\tilde{\boldsymbol{X}}_{i k}-1} \mathit{\boldsymbol{\varPhi}}_{i k}^{\mathrm{T}}+\mathit{\boldsymbol{\varSigma}}_{\boldsymbol{w}_{i k}} $

(12)

$ \boldsymbol{K}_{i k}=\mathit{\boldsymbol{\varSigma}}_{\overline{\boldsymbol{X}}_{i k}} \boldsymbol{H}_{i k}^{\mathrm{T}}\left(\boldsymbol{H}_{i k} \mathit{\boldsymbol{\varSigma}}_{\overline{\boldsymbol{X}}_{i k}} \boldsymbol{H}_{i k}^{\mathrm{T}}+\mathit{\boldsymbol{\varSigma}}_{i k}\right)^{-1} $

(13)

$ \hat{\boldsymbol{X}}_{i k}=\overline{\boldsymbol{X}}_{i k}+\boldsymbol{K}_{i k}\left(\boldsymbol{Z}_{i k}-\boldsymbol{H}_{i k} \overline{\boldsymbol{X}}_{i k}\right) $

(14)

$ \mathit{\boldsymbol{\varSigma}}_{\hat{\boldsymbol{X}}_{i k}}=\mathit{\boldsymbol{\varSigma}}_{\overline{\boldsymbol{X}}_{i k}}-\boldsymbol{K}_{i k} \boldsymbol{H}_{i k} \mathit{\boldsymbol{\varSigma}}_{\overline{\boldsymbol{X}}_{i k}} $

(15)

式中，$\overline{\boldsymbol{X}}_{i k}$和$\mathit{\boldsymbol{\varSigma}}_{\overline{\boldsymbol{X}}_{i k}}$分别为预测状态向量和预测状态协方差矩阵；$\hat{\boldsymbol{X}}_{i k}$和$\mathit{\boldsymbol{\varSigma}}_{\hat{\boldsymbol{X}}_{i k}}$分别为Kalman滤波的状态估计值和状态协方差矩阵；K_ik为Kalman滤波增益。

高精度电子地图的普及使事先获取载体运动轨迹成为可能。通过高精度电子地图可以获取道路的走向、节点坐标等信息，而实际中载体的运动轨迹又可以看成由多个直线段组合的折线。因此，当在具有道路先验信息的场合运动时，载体平面位置坐标之间存在内在约束关系^[11]，本文基于此来考虑状态约束下各个子滤波的状态估计。设某一段直线道路的起点平面坐标为(r₀^E, r₀^N)，道路的走向为北偏东θ_k度，k时刻载体运动的真实平面位置和速度分别为$\left(\widetilde{r_k^E}, \widetilde{r_k^N}, \widetilde{v}_k^E, \widetilde{v}_k^N\right)$，则存在如下约束信息：

$ \frac{\widetilde{r_k^E}-r_0^E}{\widetilde{r_k^N}-r_0^N}=\tan \theta_k $

(16)

$ \frac{\widetilde{v}_k^E}{\widetilde{v}_k^N}=\tan \theta_k $

(17)

由于本文以大地坐标系位置误差[δL, δλ, δh]作为滤波的状态量，而式(16)为导航坐标系(ENU)下的位置约束，因此还需进行误差扰动和转换。对于第i个传感器，可得如下约束方程：

$ \left[ {\begin{array}{*{20}{r}} {{{\mathbf{0}}_{1 \times 6}}}&{\left[ {\begin{array}{*{20}{r}} {1 - \tan {\theta _k}}&0 \end{array}} \right]{\mathit{\boldsymbol{C}}_{ik}}}&{{{\mathbf{0}}_{1 \times 6}}} \\ {{{\mathbf{0}}_{1 \times 3}}}&{\begin{array}{*{20}{c}} {1 - \tan {\theta _k}}&0 \end{array}}&{{{\mathbf{0}}_{1 \times 9}}} \end{array}} \right]{\mathit{\boldsymbol{X}}_{ik}} = {\mathit{\boldsymbol{d}}_{ik}} $

(18)

式中，$\boldsymbol{C}_{i k}=\left[0, \left(R_N+H\right) \cos (L), 0 ; R_M+H, 0, \right.0 ; 0, 0, 1]$，R_M和R_N分别为沿地球子午圈和卯酉圈的主曲率半径，H为当地高程，L为当地纬度。

为便于推导，将式(18)简化为：

$ \boldsymbol{D}_{i k} \boldsymbol{X}_{i k}=\boldsymbol{d}_{i k} $

(19)

式中，D_ik为s×n维行满秩约束矩阵，s为约束方程个数，n为状态估计量个数；d_ik为s维约束向量。设W_ik为任意对称的正定矩阵，则对含有等式约束的状态估计问题变成对式(20)的求解问题，即寻求满足下列方程的状态估计值$\widetilde{\boldsymbol{X}}_{i k}$：

$ \left\{\begin{array}{l} \min J\left(\tilde{\boldsymbol{X}}_{i k}\right)=\left(\tilde{\boldsymbol{X}}_{i k}-\hat{\boldsymbol{X}}_{i k}\right)^{\mathrm{T}} \boldsymbol{W}_{i k}\left(\tilde{\boldsymbol{X}}_{i k}-\hat{\boldsymbol{X}}_{i k}\right) \\ \text { s. t. } \boldsymbol{D}_{i k} \widetilde{\boldsymbol{X}}_{i k}=\boldsymbol{d}_{i k} \end{array}\right. $

(20)

通过最优化中的Lagrange乘子法求解式(20)：

$ \tilde{\boldsymbol{X}}_{i k}=\hat{\boldsymbol{X}}_{i k}-\boldsymbol{W}_{i k}^{-1} \boldsymbol{D}_{i k}^{\mathrm{T}}\left(\boldsymbol{D}_{i k} \boldsymbol{W}_{i k}^{-1} \boldsymbol{D}_k^{\mathrm{T}}\right)^{-1}\left(\boldsymbol{D}_{i k} \hat{\boldsymbol{X}}_{i k}-\boldsymbol{d}_{i k}\right) $

(21)

由式(19)可知$\boldsymbol{D}_{i k} \boldsymbol{X}_{i k}-\boldsymbol{d}_{i k}=0$，则：

$ \begin{gathered} \boldsymbol{X}_{i k}-\tilde{\boldsymbol{X}}_{i k}=\boldsymbol{X}_{i k}-\hat{\boldsymbol{X}}_{i k}+\boldsymbol{W}_{i k}^{-1} \boldsymbol{D}_{i k}^{\mathrm{T}}\left(\boldsymbol{D}_{i k} \boldsymbol{W}_{i k}^{-1} \boldsymbol{D}_{i k}^{\mathrm{T}}\right)^{-1} \\ {\left[\boldsymbol{D}_{i k} \hat{\boldsymbol{X}}_{i k}-\boldsymbol{d}_{i k}-\left(\boldsymbol{D}_{i k} \boldsymbol{X}_{i k}-\boldsymbol{d}_{i k}\right)\right]=} \\ \left(\boldsymbol{I}-\boldsymbol{W}_{i k}^{-1} \boldsymbol{D}_{i k}^{\mathrm{T}}\left(\boldsymbol{D}_{i k} \boldsymbol{W}_{i k}^{-1} \boldsymbol{D}_{i k}^{\mathrm{T}}\right)^{-1} \boldsymbol{D}_{i k}\right)\left(\boldsymbol{X}_{i k}-\hat{\boldsymbol{X}}_{i k}\right) \end{gathered} $

(22)

令$\boldsymbol{G}_{i k}=\boldsymbol{W}_{i k}^{-1} \boldsymbol{D}_{i k}^{\mathrm{T}}\left(\boldsymbol{D}_{i k} \boldsymbol{W}_{i k}^{-1} \boldsymbol{D}_{i k}^{\mathrm{T}}\right)^{-1} \boldsymbol{D}_{i k}$，则经过约束信息修正后的状态协方差可写为：$\mathit{\boldsymbol{\varSigma}}_{\tilde{\boldsymbol{X}}_{i k}}$

$ \begin{aligned} \mathit{\boldsymbol{\varSigma}}_{\tilde{\boldsymbol{X}}_{i k}}= & E\left[\left(\boldsymbol{X}_{i k}-\tilde{\boldsymbol{X}}_{i k}\right)\left(\boldsymbol{X}_{i k}-\widetilde{\boldsymbol{X}}_{i k}\right)^{\mathrm{T}}\right]= \\ & \left(\boldsymbol{I}-\boldsymbol{G}_{i k}\right) \mathit{\boldsymbol{\varSigma}}_{\hat{\boldsymbol{X}}_{i k}}\left(\boldsymbol{I}-\boldsymbol{G}_{i k}\right)^{\mathrm{T}} \end{aligned} $

(23)

通过式(21)和式(23)可以求出状态约束下子滤波器的状态估计值和估计协方差矩阵，通常情况下对称正定矩阵W_ik可以选择为单位矩阵I或者后验估计权矩阵$\mathit{\boldsymbol{\varSigma}}_{\hat{\boldsymbol{X}}_{i k}}^{-1}$^[1]。

求出各子滤波器在状态约束下的状态估计值及其协方差矩阵后，按照式(4)和式(5)融合，即可得到状态约束下联邦滤波的全局状态估计值及其协方差矩阵。

3 CON-RAFKF算法

当载体处于一些复杂环境时，传感器可能会出现观测数据缺失或因受到外界干扰使观测量出现异常的情况。为进一步提高导航系统的定位精度和可靠性，对上节提出的CON-FKF算法进行改进。首先，在各个子滤波器中加入Huber抗差方法，以抵制观测异常对导航精度的影响；其次，在信息分配阶段加入基于马氏距离的自适应信息分配因子，以进一步减小子滤波器的不准确估计对全局估计的影响^[8]。

3.1 Huber抗差方法

Huber抗差方法通过结合l₁、l₂两种范数来构建代价函数，其抗差性优于基于l₂范数的估计方法。Huber代价函数表达式为^[6]：

$ \rho\left(v_j\right)=\left\{\begin{array}{l} 0.5 v_j^2, \left|v_j\right| \leqslant \gamma \\ \gamma\left|v_j\right|-0.5 \gamma^2, \left|v_j\right|>\gamma \end{array}\right. $

(24)

式中，γ为调节因子，取值范围为^{[1, 2]}，一般取1.345^[6]；v_j为第i个传感器的观测残差，可由v_k$=\left(\mathit{\boldsymbol{\varSigma}}_{i k}\right)^{-0.5}\left[\boldsymbol{Z}_{i k}-\boldsymbol{H}_{i k}\left(\overline{\boldsymbol{X}}_{i k}\right)\right]$获得，其中j=1, 2, …, m，m为观测量的维数。

Huber权值函数表达式如下^[11]：

$ \psi\left(v_j\right)=\frac{\varphi\left(v_j\right)}{v_j}=\left\{\begin{array}{l} 1, \left|v_j\right| \leqslant \gamma \\ \frac{\gamma}{\left|v_j\right|}, \left|v_j\right|>\gamma \end{array}\right. $

(25)

式中，φ(v_j)由ρ(v_j)求导所得。

$ \tilde{\boldsymbol{\psi}}\left(v_j\right)=\operatorname{diag}\left(\psi\left(v_j\right)\right) $

(26)

利用上式对观测噪声矩阵Σ_ik进行修正，以提高系统的抗差性，修正公式为：

$ \hat{\mathit{\boldsymbol{\varSigma}}}_{i k}=\sqrt{\mathit{\boldsymbol{\varSigma}}_{i k}}\tilde{\boldsymbol{\psi}}\left(v_j\right)^{-1} \sqrt{\mathit{\boldsymbol{\varSigma}}_{i k}} $

(27)

式中，Σ_ik为第i个子滤波器的观测噪声矩阵，为对角矩阵，$\sqrt{\mathit{\boldsymbol{\varSigma}}_{i k}}$即Σ_ik对角线上元素的平方根。加入Huber抗差方法的具体滤波步骤为：1)由式(11)和式(12)计算预测状态向量和预测状态协方差矩阵；2)将式(27)修正的观测噪声矩阵$\hat{\mathit{\boldsymbol{\varSigma}}}_{i k}$替换式(13)中的Σ_ik；3)根据式(14)、(15)、(21)和(23)，计算子滤波的状态估计值和状态协方差矩阵。

3.2 计算信息分配因子

在传统的联邦滤波中，信息分配因子被设置为固定值，当子滤波器出现异常情况时，其错误的估计信息会被带入到主滤波器中，导致系统的容错性降低。因此，自适应确定信息分配因子对提高系统性能具有重要意义^{[10, 12]}。本文选取第i个子滤波的状态估计和融合后的状态估计的马氏距离作为评价子滤波器滤波效果的指标，并以此来计算信息分配因子。具体公式为：

$ \boldsymbol{M}_{i k}=\sqrt{\left(\hat{\boldsymbol{X}}_{g k}-\tilde{\boldsymbol{X}}_{i k}\right)^{\mathrm{T}} \mathit{\boldsymbol{\varSigma}}_{\hat{\boldsymbol{X}}_{g k} \overline{\boldsymbol{X}}_{i k}}\left(\hat{\boldsymbol{X}}_{g k}-\tilde{\boldsymbol{X}}_{i k}\right)} $

(28)

式中，$\mathit{\boldsymbol{\varSigma}}_{\tilde{\boldsymbol{X}}_{g k} \tilde{\boldsymbol{X}}_{i k}}$为$\hat{\boldsymbol{X}}_{g k}$和$\tilde{\boldsymbol{X}}_{i k}$的协方差矩阵。当M_ik越小时，子滤波器的状态估计值和主滤波器的估计值越接近，表示该子滤波器的状态估计效果越好，因此可以分配更多的信息给该子滤波器。信息分配因子β_i为：

$ \beta_i=\frac{M_{i k}^{-1}}{\sum\limits_i^r M_{i k}} $

(29)

4 仿真实验及分析

仿真生成SINS/GNSS/ODO数据，设置车辆的初始位置为30.46°N、114.47°E，高度22 m。IMU的陀螺零偏为0.5°/h，加速度计零偏为2 000 μ g，角度随机游走0.05°$\sqrt{\mathrm{h}}$，速度随机游走200 $\mu\;g / \sqrt{\mathrm{Hz}}$，采样频率为100 Hz。GNSS定位误差为σ_P=[5 m, 5 m, 10 m]，ODO速度误差为σ_v=[0.1 m/s, 0.1 m/s, 0.1 m/s]，采样频率均为1 Hz，仿真时长为600 s。由于复杂的运动轨迹可以看成由多个直线段组成的折线，因此本文仅针对某个直线段进行分析。设置车辆运动轨迹为北偏东30°方向的一条直线。

初始误差协方差矩阵和过程噪声矩阵设置为：

$ \begin{gathered} \mathit{\boldsymbol{\varSigma}}_{\boldsymbol{X}_0}=\operatorname{diag}\left[\left(1^{\prime}\right)^2, \left(1^{\prime}\right)^2, \left(1.5^{\prime}\right)^2, \right. \\ (0.2 \mathrm{~m} / \mathrm{s})^2 \boldsymbol{I}_{3 \times 3}, (10 \mathrm{~m})^2, (10 \mathrm{~m})^2, (20 \mathrm{~m})^2 \\ \left.\left.0.5\left({ }^\mathit{{\circ}}\right) / \mathrm{h}\right)^2 \boldsymbol{I}_{3 \times 3}, (2000 \mu \mathrm{g})^2 \boldsymbol{I}_{3 \times 3}\right] \end{gathered} $

(30)

$ \begin{gathered} \boldsymbol{Q}_k=\operatorname{diag}\left[\left(0.05^\mathit{{\circ}} / \sqrt{\mathrm{h}}\right)^2 \boldsymbol{I}_{3 \times 3}, \right. \\ \left.\quad(200 \mu\;\mathrm{g} / \sqrt{\mathrm{Hz}})^2 \boldsymbol{I}_{3 \times 3}, \mathbf{0}_{9 \times 9}\right] \end{gathered} $

(31)

观测噪声设置为：

$ \boldsymbol{R}_{1 k}=\operatorname{diag}\left[(5 \mathrm{~m})^2, (5 \mathrm{~m})^2, (10 \mathrm{~m})^2\right] $

(32)

$ \begin{aligned} & \boldsymbol{R}_{2 k}=\operatorname{diag}\left[(0.1 \mathrm{~m} / \mathrm{s})^2,\right. \\ & \left.(0.1 \mathrm{~m} / \mathrm{s})^2, (0.1 \mathrm{~m} / \mathrm{s})^2\right] \end{aligned} $

(33)

4.1 测试1

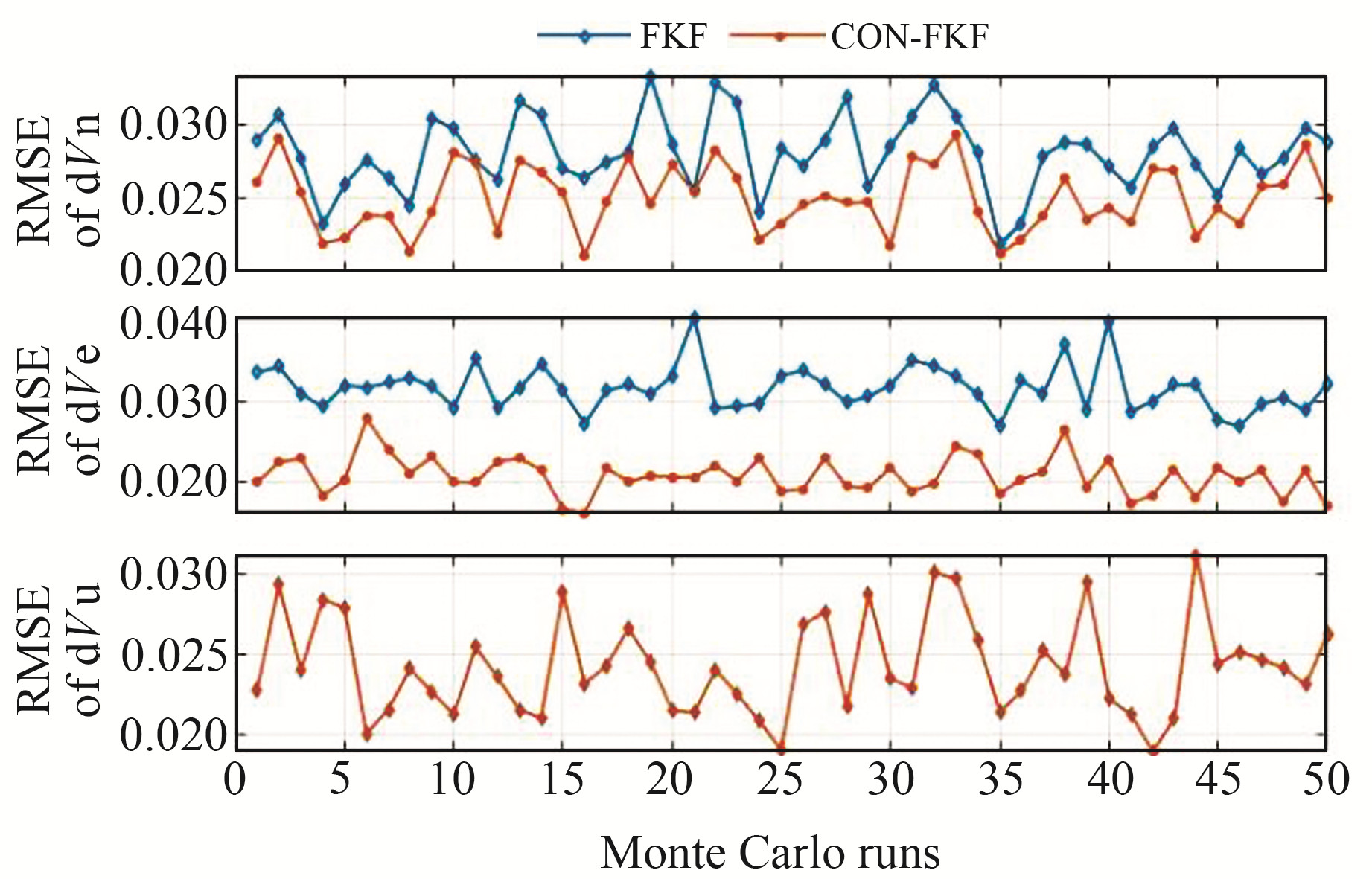
测试1主要分析加入约束条件对FKF状态估计的影响。由图 2和3可知，加入约束条件后，状态估计精度有所提高。为了防止随机性，对该系统进行50次蒙特卡洛仿真，计算50次仿真的RMSE，得到图 4和5。可以看出，加入约束条件后，水平方向位置的平均RMSE分别下降12.46%、34.27%，速度的平均RMSE分别下降10.87%、34.80%；高程方向CON-FKF与FKF相比，位置和速度的RMSE变化都很小，这是由于本文采用的约束信息仅针对水平方向，在高程方向没有约束信息。

4.2 测试2

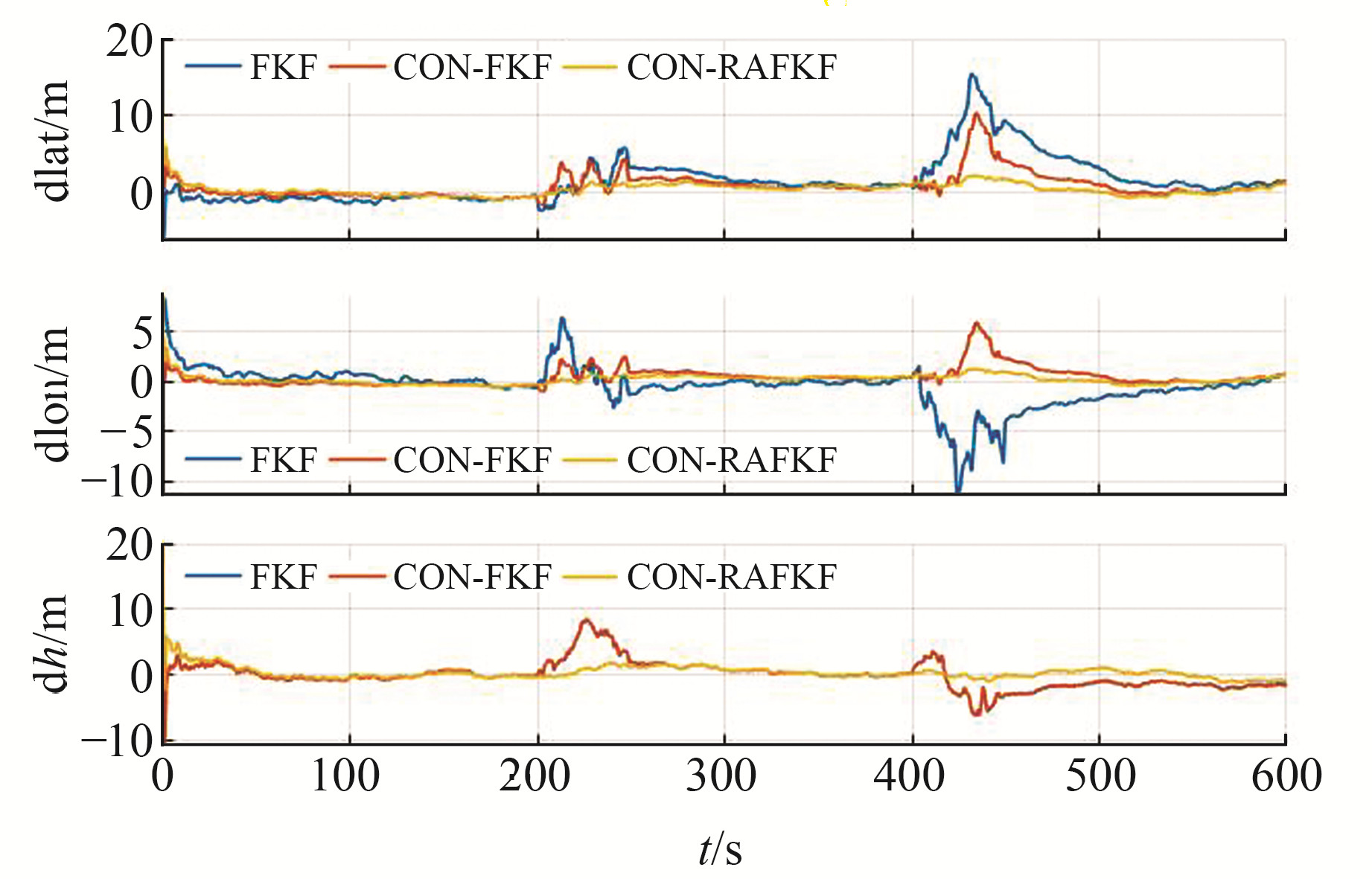
测试2主要是分析本文算法在SINS/GNSS/ODO组合导航系统出现异常时的性能(图 6和7)。在200~250 s，模拟ODO观测异常，将10σ_v加入到ODO观测的速度上，σ_v=[0.1 m/s, 0.1 m/s, 0.1 m/s]；在400~450 s，模拟GNSS观测异常，将10σ_p加入GNSS观测的位置上，σ_p=[5 m, 5 m, 10 m]。

由图 6和7可知，FKF无法处理观测情况，会把误差信息带入到最终融合解中，致使导航系统的准确性下降；CON-FKF由于加入了先验约束信息，在一定程度上抑制了观测异常；CON-RAFKF在CON-FKF的基础上进一步加入了Huber抗差方法和自适应信息分配因子，与前2种算法相比，能够更好地应对观测异常的情况。

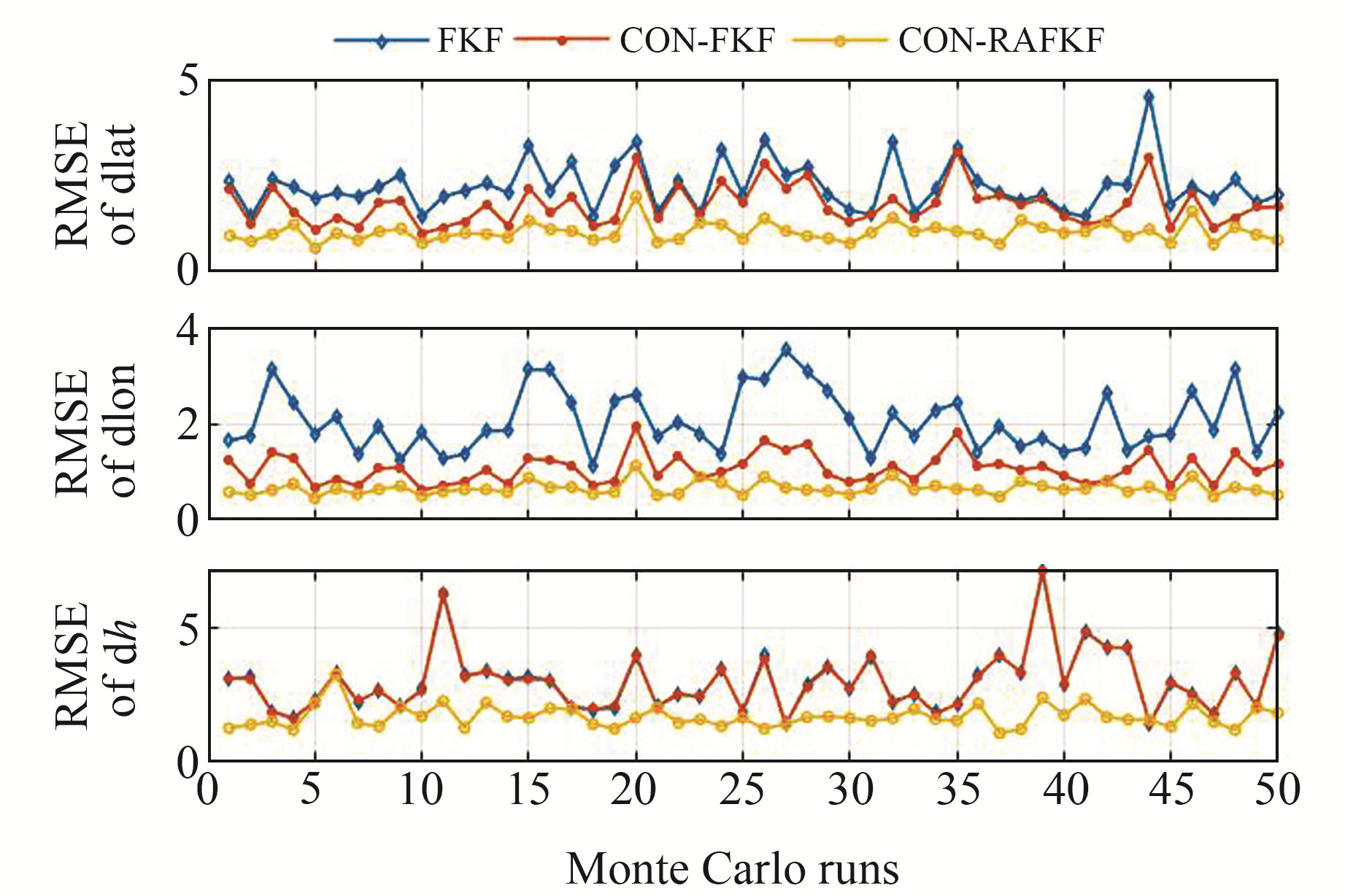
同样，对观测异常情况下的导航系统进行50次蒙特卡洛仿真，其RMSE结果见图 8和9，平均RMSE统计结果见表 1。可以看出，与FKF相比，CON-RAFKF三方向的位置平均RMSE分别下降53.84%、68.12%、43.37%，速度平均RMSE分别下降40.05%、62.25%、39.21%；与CON-FKF相比，CON-RAFKF三方向的位置平均RMSE分别下降40.58%、38.60%、43.30%，速度平均RMSE分别下降26.11%、44.75%、39.07%，可见CON-RAFKF显著提高了系统的定位精度和可靠性。

5 结语

针对多传感器导航系统中状态量之间存在先验约束信息的情形，本文提出一种状态约束的联邦卡尔曼滤波算法。此外，当观测量出现异常时，本文将Huber抗差方法及自适应信息分配策略加入到状态约束下的联邦卡尔曼滤波中。理论分析和仿真实验表明，在联邦卡尔曼滤波中，考虑先验约束条件能够有效提高组合导航系统的定位精度；在带有约束条件的联邦卡尔曼滤波中，加入Huber抗差方法及自适应信息分配策略能够进一步提高复杂环境下组合导航系统的定位精度和可靠性。