随着微机电系统(MEMS)惯性测量单元(IMU)的发展,低成本GNSS/MEMS IMU组合导航系统被广泛应用到车载导航中。GNSS/INS组合导航能够输出连续的三维位置、速度和姿态信息,GNSS和INS通常采用卡尔曼滤波进行数据融合,以GNSS和INS输出的位置差值作为观测量,以导航误差和惯性传感器误差作为系统状态。惯性传感器的典型误差包括零偏误差和比例因子误差等,在构建系统状态模型时,部分学者仅考虑了陀螺仪和加速度计的零偏误差[1],也有学者研究增广了陀螺仪和加速度计的比例因子误差(以下简称比例因子误差)[2-3]。Godha[4]研究了比例因子误差对GNSS/MEMS IMU车载组合导航的影响,结果发现,增广比例因子误差能够明显减小水平和高程误差。然而,Godha仅使用一款比例因子误差为10-2的MEMS IMU,并未评估不同大小的比例因子误差对车载导航精度的影响。由于EKF算法的计算量与系统状态维数的三次方成正比[5],增广比例因子误差会显著增加组合导航计算量。因此,需要在同时考虑计算量和精度提升两方面因素的前提下,研究增广比例因子误差的必要性,在保证导航精度的前提下降低系统状态的维数。部分学者提出了降维状态模型,但没有考虑系统状态中的比例因子误差[6-7]。
基于此,本文围绕卡尔曼滤波的系统状态模型,分析比例因子误差对导航精度和组合导航计算量的影响。同时,通过分析车载动态下比例因子误差的可观测性,提出一种仅保留航向陀螺仪、水平加速度计比例因子误差的降维状态模型,通过半物理仿真实验评估比例因子误差对导航精度的影响及状态模型降维的效果。
1 卡尔曼滤波的系统状态模型GNSS/INS组合导航卡尔曼滤波的状态微分方程可表示为:
| $ \delta \dot{\boldsymbol{x}}(t)=\boldsymbol{F}(t) \delta \boldsymbol{x}(t)+\boldsymbol{G}(t) \boldsymbol{n}(t) $ | (1) |
式中,δx为系统状态变量,F为反馈矩阵,G为噪声驱动矩阵。系统状态中包含导航状态误差和IMU测量误差。导航状态误差包含三维位置误差、三维速度误差、三维姿态误差。IMU测量误差建模为:
| $ \delta \boldsymbol{\omega}_{i b}^b=\boldsymbol{b}_g+\boldsymbol{s}_g \boldsymbol{\omega}_{i b}^b+\boldsymbol{n}_g $ | (2) |
| $ \delta \boldsymbol{f}^b=\boldsymbol{b}_a+\boldsymbol{s}_a \boldsymbol{f}^b+\boldsymbol{n}_a $ | (3) |
式中,bg为陀螺仪零偏误差,ba为加速度计零偏误差,sg为陀螺仪比例因子误差,sa为加速度计比例因子误差,ng为陀螺仪噪声,na为加速度计噪声,ωibb为b系下陀螺仪输出的理论角速度,fb为b系下加速度计感知的理论比力。若仅考虑陀螺仪和加速度计的零偏误差,则卡尔曼滤波的系统状态为15维(以下简称15维状态模型):
| $ \delta \mathit{\boldsymbol{x}} = {\left[ \left(\delta \boldsymbol{r}^n\right)^{\mathrm{T}} \quad\left(\delta \boldsymbol{v}^n\right)^{\mathrm{T}} \quad(\boldsymbol{\varphi})^{\mathrm{T}} \quad\left(\boldsymbol{b}_g\right)^{\mathrm{T}} \quad\left(\boldsymbol{b}_a\right)^{\mathrm{T}} \right]^{\rm{T}}} $ | (4) |
若同时考虑陀螺仪和加速度计的比例因子误差,则卡尔曼滤波的系统状态为21维(以下简称21维状态模型):
| $ \begin{array}{l} \delta \boldsymbol{x}=\left[\begin{array}{llll} \left(\delta \boldsymbol{r}^n\right)^{\mathrm{T}} \left(\delta \boldsymbol{v}^n\right)^{\mathrm{T}} (\boldsymbol{\varphi})^{\mathrm{T}} \left(\boldsymbol{b}_g\right)^{\mathrm{T}} \end{array}\right. \\\;\;\;\;\;\;\;\;\;\;\; \left.\left(\boldsymbol{b}_a\right)^{\mathrm{T}} \quad\left(\boldsymbol{s}_g\right)^{\mathrm{T}}\left(\boldsymbol{s}_a\right)^{\mathrm{T}}\right]^{\mathrm{T}} \\ \end{array} $ | (5) |
由于MEMS IMU的比例因子误差较大[8],车辆运动时角度和速度变化较为剧烈,陀螺仪和加速度计有较大输出,理论上比例因子误差会对导航精度产生较大影响。
组合导航滤波运算的数据一般以双精度浮点形式存储,可以采用浮点运算次数来衡量滤波的计算量。组合导航卡尔曼滤波的浮点运算次数C与系统状态维数n的关系式为[9]:
| $ C=10 n^3-8 n^2+64 n+54 $ | (6) |
由式(6)可知,15维状态模型的卡尔曼滤波(以下简称15维滤波)浮点运算次数为32 964次,21维状态模型的卡尔曼滤波(以下简称21维滤波)浮点运算次数为90 480次。因此,增广比例因子误差会导致计算量增加约170%。
2 降维的系统状态模型Davison[10]研究表明,不可观测的状态对系统的影响极小,因此本文忽略车载运动中部分观测性较弱的比例因子误差,以实现21维状态模型的降维。此外,在车载动态下,部分比例因子误差与零偏误差具有强相关性,忽略此类比例因子误差也有助于降维。
2.1 sg,x与sg,y的观测性分析载体的姿态可以用一组姿态角表示,车载运动的俯仰角和横滚角近似为0,车辆姿态的变化与陀螺仪三轴输出的关系可表示为:
| $ \left[\begin{array}{l} \dot{\varphi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right]=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} \boldsymbol{\omega}_{n b, x}^b \\ \boldsymbol{\omega}_{n b, y}^b \\ \boldsymbol{\omega}_{n b, z}^b \end{array}\right]=\left[\begin{array}{l} \boldsymbol{\omega}_{n b, x}^b \\ \boldsymbol{\omega}_{n b, y}^b \\ \boldsymbol{\omega}_{n b, z}^b \end{array}\right] $ | (7) |
式中,φ为横滚角,θ为俯仰角,ψ为航向角。若忽略地球自转角速度ωien、牵连角速度ωenn及车辆的安装角,ωnb,xb近似为陀螺仪x轴(横滚陀螺仪)角速度测量输出,ωnb,yb近似为陀螺仪y轴(俯仰陀螺仪)角速度测量输出,ωnb,zb近似为陀螺仪z轴(航向陀螺仪)角速度测量输出。由式(7)可知,陀螺仪x轴输出真值积分近似为横滚角,陀螺仪y轴输出真值积分近似为俯仰角。由于车载运动的俯仰角和横滚角近似为0,因此陀螺仪x轴和y轴输出的真值近似为0。由于横滚陀螺仪比例因子误差sg,x与俯仰陀螺仪比例因子误差sg,y为乘性干扰,对陀螺仪x轴和y轴输出的影响较小,二者可观测性较弱,因此在21维状态模型中可以忽略sg,x和sg,y。
2.2 ba,z与sa,z的强相关性分析由于车载运动的俯仰角θ和横滚角φ近似为0,因此INS系统中加速度计三轴的输出为:
| $ \left[\begin{array}{l} \boldsymbol{f}_x^b \\ \boldsymbol{f}_y^b \\ \boldsymbol{f}_z^b \end{array}\right]=\left[\begin{array}{c} \boldsymbol{a}_{e b, x}^b \\ \boldsymbol{a}_{\phi, y}^b \\ \boldsymbol{a}_{t b, z}^b-\boldsymbol{g}_l^b \end{array}\right] $ | (8) |
式中,aebb为载体坐标系(b系)相对于地球坐标系(e系)的加速度在b系下的投影,glb为当地的重力加速度在b系下的投影。由式(8)可知,在车载运动中,加速度计z轴(高程加速度计)的输出在-glb左右波动,且比例因子误差与常值输出的乘积可以等效为零偏误差。因此,在车载运动中,高程加速度计零偏误差ba,z和高程加速度计比例因子误差sa,z具有强相关性,在21维状态模型中可忽略sa,z。
上述分析表明,在顾及精度的情况下,理论上可以将21维状态模型降维为18维状态模型,即
| $\begin{array}{c} \delta \boldsymbol{x}=[ \left(\delta \boldsymbol{r}^n\right)^{\mathrm{T}} \quad\left(\delta \boldsymbol{v}^n\right)^{\mathrm{T}} \quad(\boldsymbol{\varphi})^{\mathrm{T}} \quad\left(\boldsymbol{b}_g\right)^{\mathrm{T}} \quad\left(\boldsymbol{b}_a\right)^{\mathrm{T}}\\ \begin{aligned} & \left.\begin{array}{lll} \boldsymbol{S}_{g, z} & \boldsymbol{S}_{a, x} & \boldsymbol{S}_{a, y} \end{array}\right]^{\mathrm{T}} \end{aligned}\end{array} $ | (9) |
式中,sg,z为航向陀螺仪比例因子误差,sa,x与sa,y为水平2轴加速度计比例因子误差。
由式(9)可知,18维状态模型的卡尔曼滤波(以下简称18维滤波)浮点运算次数为56 934次,18维滤波相对于15维滤波仅增加约70%的计算量。
3 仿真实验验证为了评估比例因子误差对导航精度的影响及模型降维的效果,本文使用武汉大学多源智能导航实验室的组合导航仿真平台进行仿真实验。该仿真软件使用真实轨迹输入,可反映真实运动状态,具有较高可信度。实验过程如下:1)查阅多款MEMS IMU数据手册,确定10组不同大小的比例因子误差用于仿真,最小为2×10-3,最大为2×10-2;2)使用导航级GNSS/INS组合导航系统POS-A15,采集真实车载运动轨迹与GNSS观测数据;3)利用车载运动轨迹反推出IMU真值,并添加仿真IMU误差,得到不同比例因子误差的10组仿真数据。仿真时,各种误差正负随机(为简化描述,后文陈述误差时使用其绝对值),各组除比例因子外的其他误差相同,误差确定参考一款典型的MEMS IMU(ICM20602,InvenSense)。
3.1 比例因子误差影响分析为评估比例因子误差对导航精度的影响,使用仿真数据与GNSS观测数据进行组合导航解算,每组仿真数据分别使用15维滤波和21维滤波解算2次,通过统计各组GNSS模拟中断漂移量,评估导航精度。GNSS模拟中断的周期为180 s,每个周期中断60 s。中断漂移的均方值(RMS)如表 1(单位m)所示。
|
|
表 1 中断漂移的RMS值 Tab. 1 The RMS value of interruption drift |
由表 1可见,水平漂移均明显大于高程漂移,水平误差是主要误差因素,因此本文使用水平漂移评估导航精度。当比例因子误差大于等于5×10-3时,21维滤波相对于15维滤波的水平漂移减小比例最大仅5.05%,而计算量却增加170%;当比例因子误差大于6×10-3时,21维滤波相对于15维滤波的水平漂移减小比例超过10%。因此,只有当比例因子误差大于6×10-3时,才有必要增广比例因子误差。
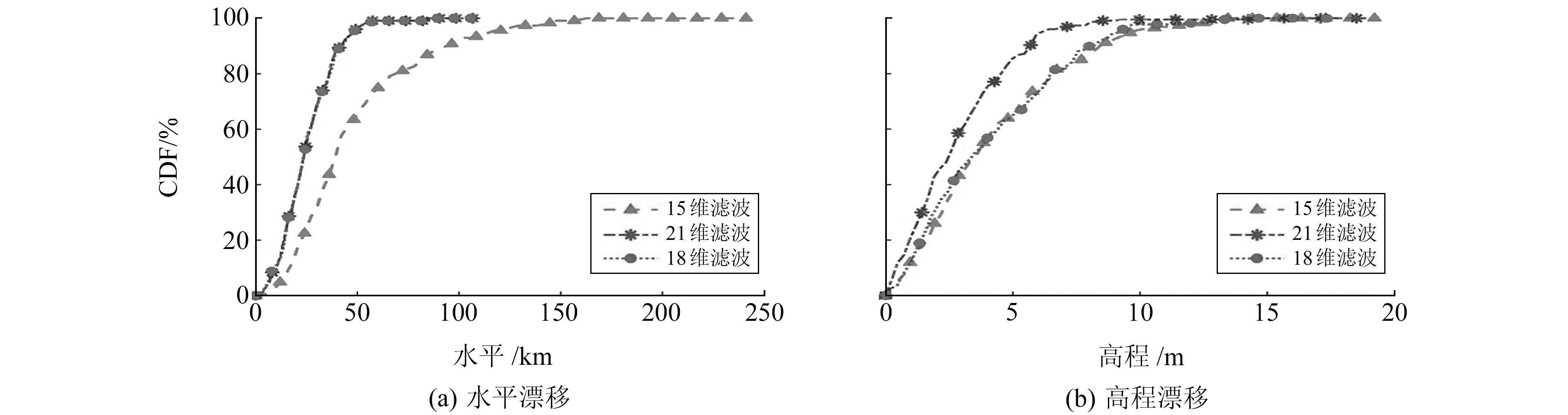
3.2 模型降维的效果分析在§3.1的基础上,使用比例因子误差为2×10-2的数据进行18维滤波处理,并统计其中断漂移结果。15维滤波、18维滤波和21维滤波的中断漂移累积分布函数曲线(CDF曲线)如图 1所示。
|
图 1 15、18和21维滤波中断漂移CDF曲线 Fig. 1 Filter interruption drift CDF curves of 15, 18, and 21-dimensional filter |
由图 1(a)可知,18维滤波和21维滤波的水平漂移CDF曲线几乎一致,均优于15维滤波;由图 1(b)可知,18维滤波和15维滤波的高程漂移CDF曲线接近,稍差于21维滤波。由于车载导航主要关心水平方向位置精度,因此可认为18维状态模型和21维状态模型导航精度相当。
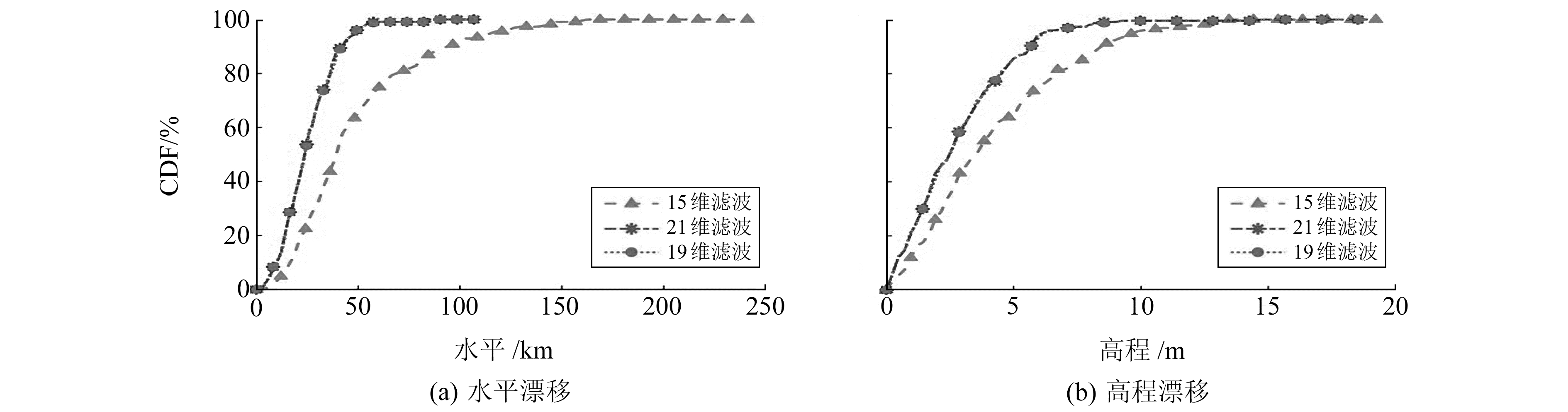
此外,高程误差主要受加速度计z轴误差的影响,忽略sa,z会造成18维滤波的高程误差较大。如需关注高程精度,则可忽略sg,x、sg,y,保留sg,z,得到19维状态模型。使用比例因子误差为2×10-2的仿真数据进行19维状态模型的卡尔曼滤波(以下简称19维滤波)处理,并统计其中断漂移结果。15维滤波、19维滤波与21维滤波的中断漂移CDF曲线如图 2所示,由图可见,19维滤波的水平、高程漂移CDF曲线与21维滤波几乎完全重合,均明显优于15维滤波。
|
图 2 15、19和21维滤波中断漂移CDF曲线 Fig. 2 Filter interruption drift CDF curves of 15, 19, and 21-dimensional filter |
本文围绕IMU比例因子误差对GNSS/MEMS IMU车载组合导航的影响,提出一种忽略弱可观测比例因子误差的降维模型。半物理仿真实验表明:1)当比例因子误差大于6×10-3时才有必要增广比例因子误差,但会使计算量增加约170%;2)比例因子误差中仅有航向陀螺仪和水平加速度计比例因子误差强可观测;3)忽略弱可观测比例因子误差的降维模型与保留全部比例因子误差的高维模型导航精度相当,计算量相比于不增广比例因子误差时仅增加70%。
| [1] |
Chen C, Chang G B. Low-Cost GNSS/INS Integration for Enhanced Land Vehicle Performance[J]. Measurement Science and Technology, 2020, 31(3)
(  0) 0) |
| [2] |
章红平, 常乐, 汪宏晨, 等. GNSS/INS紧组合算法实时性改进与嵌入式验证[J]. 东南大学学报: 自然科学版, 2016, 46(4): 695-701 (Zhang Hongping, Chang Le, Wang Hongchen, et al. Improvement and Verification of Real-Time Performance of GNSS/INS Tightly Coupled Integration in Embedded Platform[J]. Journal of Southeast University: Natural Science Edition, 2016, 46(4): 695-701)
(  0) 0) |
| [3] |
Moussa M, Moussa A, Elhabiby M, et al. Wheel-Based Aiding of Low-Cost IMU for Land Vehicle Navigation in GNSS Challenging Environment[C]. 2020 IEEE 92nd Vehicular Technology Conference, Victoria, 2021
(  0) 0) |
| [4] |
Godha S. Performance Evaluation of Low Cost MEMS-Based IMU Integrated with GPS for Land Vehicle Navigation Application[J]. UCGE Report, 2006
(  0) 0) |
| [5] |
秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2015 (Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Kalman Filter and Integrated Navigation Principle[M]. Xi'an: Northwestern Polytechnical University Press, 2015)
(  0) 0) |
| [6] |
胡彬, 杨新民, 王胜红. 基于降阶卡尔曼滤波算法在组合导航上的应用[J]. 电子设计工程, 2017, 25(15): 98-101 (Hu Bin, Yang Xinmin, Wang Shenghong. The Application of Reduced Order Kalman Filter Algorithm in Integrated Navigation[J]. Electronic Design Engineering, 2017, 25(15): 98-101)
(  0) 0) |
| [7] |
Banerjee S, Chattaraj S. Performance Evaluation of a Reduced Order Kalman Filter for Running Train Localization Problem[C]. 2017 International Conference on Computer, Electrical and Communication Engineering(ICCECE), Kolkata, 2018
(  0) 0) |
| [8] |
Quinchia A G, Falco G, Falletti E, et al. A Comparison between Different Error Modeling of MEMS Applied to GPS/INS Integrated Systems[J]. Sensors, 2013, 13(8): 9 549-9 588 DOI:10.3390/s130809549
(  0) 0) |
| [9] |
周翟和, 刘建业, 赖际舟, 等. 混合高斯粒子滤波在组合导航中应用的计算量分析[J]. 中国惯性技术学报, 2010, 18(5): 595-599 (Zhou Zhaihe, Liu jianye, Lai jizhou, et al. Computational Complexity of Mixture Gaussian Particle Filter about Application in Integrated Navigation[J]. Journal of Chinese Inertial Technology, 2010, 18(5): 595-599)
(  0) 0) |
| [10] |
Davison E. A Method for Simplifying Linear Dynamic Systems[J]. IEEE Transactions on Automatic Control, 1966, 11(1): 93-101 DOI:10.1109/TAC.1966.1098264
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44


