2. 国能宝日希勒能源有限公司,内蒙古自治区呼伦贝尔市神宝路751号,021599;
3. 扎赉诺尔煤业有限责任公司,内蒙古自治区呼伦贝尔市育林街17号,021410
在工程测量中,GPS测量所取得的大地高是地面点沿法线到WGS-84参考椭球面的距离。为了将大地高转化为工程测量中所需要的正常高,就需要进行GPS高程拟合,通常情况下采取拟合的方式对高程异常值进行求解。目前主要采取的方法有多项式拟合、多面函数拟合、BP神经网络、Kriging插值及分区拟合等[1-2]。由于BP神经网络法能够极大降低模型误差的干扰,近年来得到广泛应用,但该方法也存在一定弊端。首先,BP神经网络权值是沿局部方向逐渐调整,容易陷入局部极值;其次,由于其依靠梯度下降机制进行信息传递,当网络结构复杂、隐含层数目设定较多时容易出现梯度消失,导致收敛速度缓慢[3]。基于上述问题,本文提出一种改进的鲸鱼算法(chaotic mapping adaptive inertia weight whale optimization algorithm,CIWOA)优化BP神经网络,采用混沌映射和自适应惯性权重相结合的策略提升标准鲸鱼算法(WOA)的收敛速度和全局寻优能力,利用改进鲸鱼算法求得BP神经网络各层级间的网络权值和阈值的最优解,在此基础上建立改进鲸鱼算法优化BP神经网络的GPS高程异常拟合预测模型,并通过两组不同地形工程实例中的GPS数据对模型精度和稳定性进行检验。
1 改进鲸鱼算法 1.1 鲸鱼算法鲸鱼算法是Mirgalili等[4]模仿自然界中座头鲸独有的捕猎方式而诞生的一种元启发式群体智能优化算法。该算法包括收缩包围、释放气泡、随机搜索3个阶段。
1) 收缩包围。鲸鱼算法中每头鲸鱼的位置向量代表一个解,随迭代次数的增加,鲸鱼个体不断更新位置朝猎物靠近,实现收缩包围猎物[5]。用数学公式表示为:
| $ X(t+1)=X_b(t)-A \cdot D $ | (1) |
式中,Xb为当前鲸鱼种群内最优个体的位置;t为当前迭代次数;A和D为系数参数,用数学公式分别表示为:
| $ A=2 a r_1-a $ | (2) |
| $ D=\left|C \cdot X_b(t)-X_b(t)\right| $ | (3) |
式中,C=2r2, r1和r2为[0, 1]内的随机数,$a=2-\frac{2 t}{T_{\max }}$, Tmax为最大迭代次数。参数a与迭代次数遵循线性递减的关系,实现对猎物的收缩包围。
2) 释放气泡。当A<1、P<0.5时,按式(1)更新位置,P>0.5时释放气泡按螺旋轨迹上升的方式更新位置,P为[0, 1]内均匀分布的概率因子。数学公式为:
| $ X(t+1)=D^{\prime} \cdot e^{b l} \cdot \cos (2 \pi l)+X_b(t) $ | (4) |
式中,D′=Xb(t)-X(t)表示当前最优鲸鱼个体位置与猎物位置之间的距离,l为[-1, 1]内的随机数,b为螺旋线状常数,本文取1。
3) 随机搜索。当A≥1时,设定鲸鱼以随机搜索的方式进行捕猎:
| $ D_{\text {rand }}=\left|C \cdot X_{\text {rand }}(t)-X(t)\right| $ | (5) |
| $ X(t+1)=X_{\text {rand }}(t)-A \cdot D_{\text {rand }} $ | (6) |
式中,Xrand为种群内随机个体位置;Drand为鲸鱼彼此之间的距离,且随机更新,此时鲸鱼将改变之前的移动方向,随机向其他方向移动并更新位置。
1.2 Logistic-Tent映射种群初始化初始种群的优劣是影响该算法精度和收敛速度的关键因素,多样性较好的初始种群可提升算法的性能[6]。标准鲸鱼算法的设定是以一个随机方式产生初始种群,由于随机性较大导致初始种群的多样性较差,初始种群无法均匀分布在搜索空间内,限定了算法的寻优范围。
为加强标准鲸鱼算法的种群多样性,并提高算法的寻优效率,CIWOA算法采用混沌映射初始化种群策略。利用混沌变量的随机性、遍历性特点,生成多样性较好的混沌初始种群,选择迭代速度更快、遍历性和均匀性更好的Logistic-Tent混沌映射初始化种群。将混沌映射生成的混沌序列映射到解空间内得到多样性更好的初始鲸鱼种群,从而扩大算法寻优搜索范围。
Logistic-Tent映射鲸鱼初始种群步骤如下:
1) 根据所要优化的BP神经网络设置初值y0的取值范围,生成此范围内的N个值,确定参数r的值。
2) N0=y0(i), i=1, 2, …, N。
3) y(1)=N0, yi+1由式(7)求得:
| $ y_{i+1}=\left\{\begin{array}{l} {\rm{mod}} \left[r y_i\left(1-y_i\right)+\frac{4-r}{2} y_i, 1\right], \\\;\;\;\; y_i \in[0, 0, 5] \\ {\rm{mod}} \left[r y_i\left(1-y_i\right)+\frac{(4-r)\left(1-y_i\right)}{2}, 1\right], \\ \;\;\;\; y_i \in[0, 5, 1] \end{array}\right. $ | (7) |
式中,r为控制参数,r∈(0, 4),yi∈[0, 1]。混沌序列产生,即在yi∈[0, 1)内生成第i个混沌值,由式(7)共生成N个混沌值,组成混沌序列。根据式(8)将混沌序列映射到初始种群搜索空间内:
| $ x_{i j}=l_{b_j}+y_{i j}\left(u_{b_j}-l_{b_j}\right) $ | (8) |
式中,xij表示个体i在j维度初始种群空间内的位置,ub、lb分别表示初始种群的上、下边界。
4) 保存y序列并映射到解空间内得到鲸鱼初始种群,进入鲸鱼算法主循环。
1.3 自适应惯性权重权重对群体智能优化算法的全局探索和局部搜索能力的平衡起着重要作用,对算法的收敛速度和寻优能力有较大影响。WOA算法在进行寻优时权重设计为定值,并不能满足WOA算法优化过程中复杂的非线性变化。受PSO算法的启发[7],考虑到当前鲸鱼个体适应度值和鲸鱼种群平均适应度值的关系,本文提出一种非线性自适应权重的策略,其数学模型为:
| $ w=\left\{\begin{array}{l} w_s+\left(w_b+w_s\right) \cdot \mathrm{e}^{\left(-\frac{t}{T_{\max }}\right)}, f \geqslant f_{\text {avg }} \\ w_s+\frac{w_b+w_s}{T_{\max }} \cdot \mathrm{e}^{f_{\text {avg }}-f}, f <f_{\text {avg }} \end{array}\right. $ | (9) |
式中,wb、ws分别为初始最大惯性权重和初始最小惯性权重,Tmax为最大迭代次数,t为当前迭代次数,f为当前鲸鱼个体适应度值,favg为当前鲸鱼种群平均适应度值。
由式(9)得到,当鲸鱼个体适应度值大于或等于所有鲸鱼个体平均适应度值时,w值较大,使算法可在全局空间内进行大范围搜索,加快算法的收敛速度;当鲸鱼个体适应度值小于鲸鱼种群平均适应度值时,w值较小,目的使算法在最优目标附近进行小范围仔细搜索,避免陷入局部最优。
本文采用BP神经网络的均方误差函数作为CIWOA算法的适应度值函数。当高程拟合值与真实值越接近,训练误差(鲸鱼个体适应度值)越小。当训练误差达到预设目标时,可认为当前适应度值最小的鲸鱼个体的位置向量即为最优目标解,记录其空间位置向量并输出结果。
根据式(9)调整鲸鱼个体更新位置方式的公式,如式(10)~式(12)所示:
| $ X(t+1)=w \cdot X_b(t)-A \cdot D $ | (10) |
| $ \begin{gathered} X(t+1)= \\ D^{\prime} \cdot e^{b l} \cdot \cos (2 \pi l)+w \cdot X_b(t) \end{gathered} $ | (11) |
| $ X(t+1)=w \cdot X_{\text {rand }}(t)-A \cdot D_{\text {rand }} $ | (12) |
其中,w值会随着当前个体适应度值和种群平均适应度值进行自适应变化调整,以提高标准鲸鱼算法的全局搜索寻优、跳出局部最优的能力,加快算法收敛速度。
1.4 算法步骤CIWOA算法步骤如下:
1) 种群规模为N,最大迭代次数为Tmax,当前迭代次数t=0,初始最大惯性权重为wb,初始最小惯性权重为ws;
2) 计算当前所有鲸鱼个体的适应度值,记录适应度值最小的鲸鱼个体及其对应的空间位置向量;
3) 随算法迭代计算更新种群内每个鲸鱼个体的A、C、W、l值;
4) 若A≥1,鲸鱼个体根据式(12)更新下一代位置;若A<1, 鲸鱼个体根据式(10)和式(11)更新下一代位置;
5) 判断算法是否满足终止循环条件,若满足,则进入步骤6),否则返回步骤2);
6) 终止循环,输出最优目标解。
2 CIWOA-BP高程异常拟合预测模型 2.1 CIWOA优化BP神经网络原理BP神经网络作为一种多层前馈神经网络,其网络结构由输入层、隐含层、输出层构成。BP神经网络训练结果精度的高低与其初始化权值和阈值的设定有着密不可分的联系。不同的初始化权值和阈值会出现不同的结果,同时由于初始化权值和阈值具有随机性,因此难以取得理想的结果[8-9]。
本文利用CIWOA算法在全局寻优的特性,优化BP神经网络初始权值和阈值,将得到的最优神经网络权值和阈值传递给BP神经网络训练模型,从而达成BP神经网络收敛速度和精度提升的目的。将该方法称为CIWOA-BP。
2.2 建立CIWOA-BP的GPS高程异常拟合预测模型以CIWOA-BP建立GPS高程拟合模型参数设置的步骤如下:
1) 确定BP神经网络结构, 得到初始化BP神经网络的权值和阈值;
2) 对输入样本数据归一化处理,防止出现“大数吃小数”的情况;
3) 利用CIWOA算法完成初始化种群,将步骤1)得到的初始化网络权值和阈值转化为鲸鱼个体的空间位置向量,以BP神经网络的均方误差函数作为改进鲸鱼算法的适应度函数;
4) 计算种群内所有鲸鱼个体的适应度值,找出当前最优适应度值个体,记录其位置向量并作为当前最优个体;
5) 根据A的值决定鲸鱼个体更新位置的方式,当A<1时按公式(10)和式(11)更新下一代位置;当A≥1时按公式(12)更新下一代位置;
6) 当达到最大迭代次数Tmax时停止寻优算法,将当前最优权值和阈值赋值给BP神经网络。
CIWOA-BP算法流程如图 1所示。
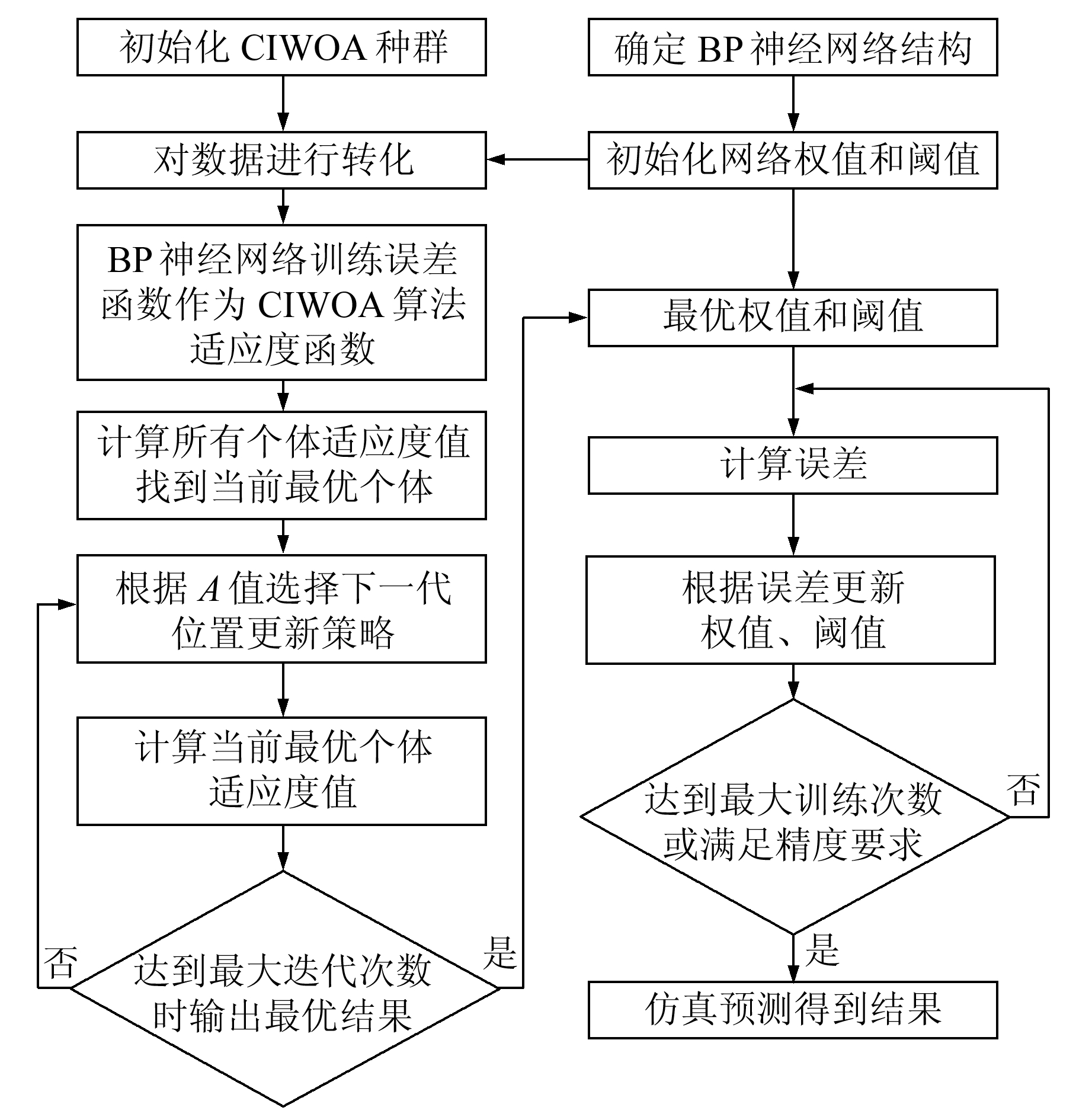
|
图 1 CIWOA算法优化BP流程 Fig. 1 Flow of CIWOA algorithm to optimize BP |
根据本文GPS高程拟合模型的特点确定BP神经网络结构为2-5-1,输入层、输出层节点个数由GPS高程拟合特点决定,通过对比分析确定隐含层节点个数。根据确定的BP神经网络结构求得CIWOA算法鲸鱼种群规模为20,CIWOA算法其他参数设置见表 1。
|
|
表 1 CIWOA-BP参数设置 Tab. 1 CIWOA-BP parameter settings |
当建模点位置均匀分布于整个测区时,所取得的高程拟合精度更高[10]。本文实验中建模点的选取遵循这一准则,即参与GPS高程拟合的建模点应均匀地分布在整个测区中。
本文采用两组不同地形测区的实测GPS水准点数据验证CIWOA-BP模型的高程拟合精度和稳定性。工程实例1为沿海狭长带状区域,地形较为平坦;工程实例2为高原内陆面状区域,地形起伏较大。为充分验证CIWOA-BP模型的精度及稳定性,在两组不同地形工程实例数据的基础上增加BP模型和WOA-BP模型,并分别从以下两个方面进行对比验证:
1) 对WOA-BP、CIWOA-BP两种模型的收敛速度和最佳适应度分别进行比较,最佳适应度即模型的均方误差,以最佳适应度大小检验两种模型的精度。
2) 将BP、WOA-BP、CIWOA-BP三种模型进行5次独立实验,对各模型的拟合残差平均值及外符合精度平均值进行评定,以检验不同模型的稳定性。
3.2 沿海狭长带状测区数据来源于杭州跨海大桥工程项目[10]中的实测GPS控制网数据。测区长约36 km,宽约30 m,共有38个GPS水准重合点(满足三等及以上水准精度要求)。在高程拟合过程中选取28个均匀分布在测区内的点作为建模点组,剩余10个点作为验证点组。点位分布情况如图 2所示。
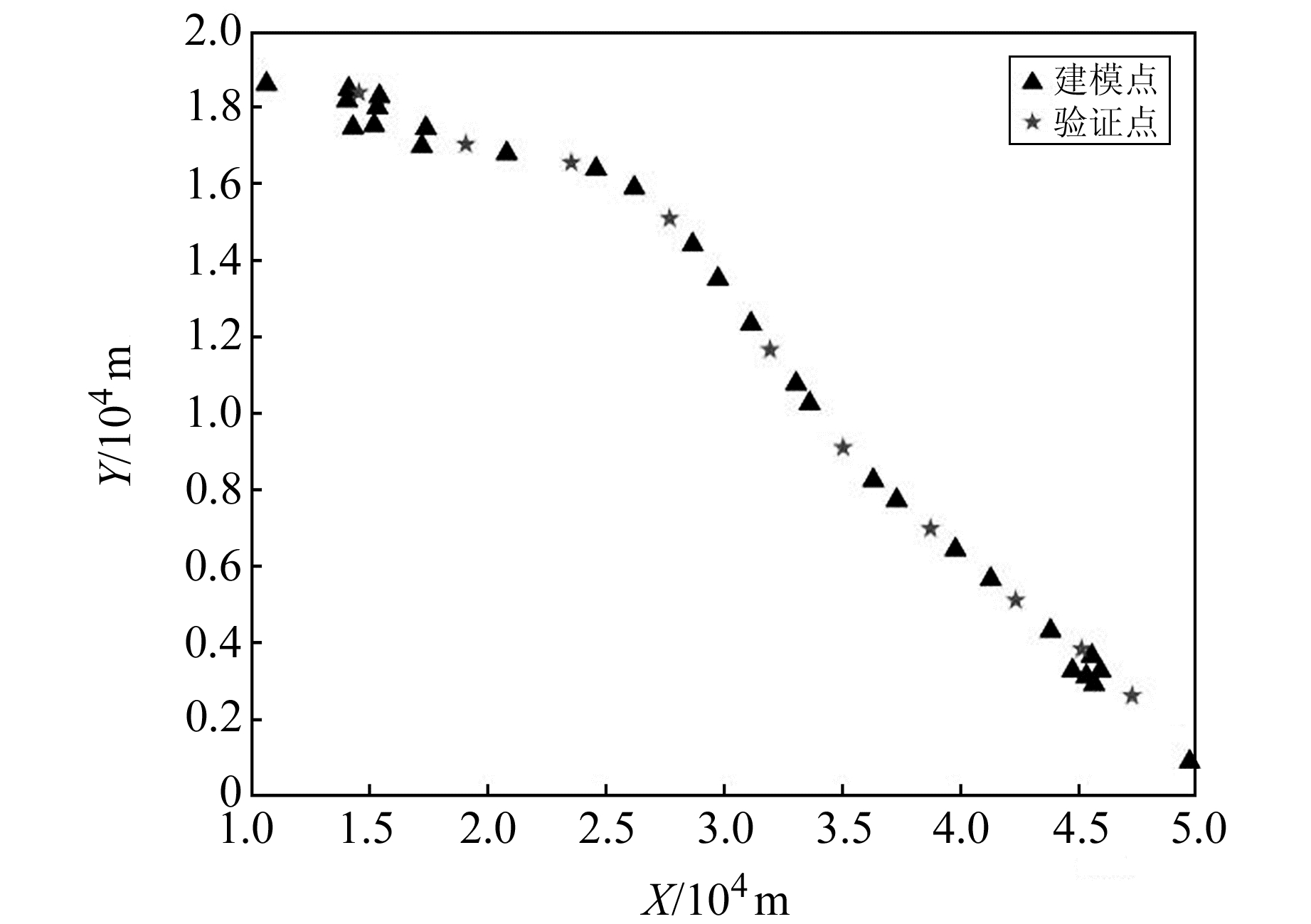
|
图 2 点位分布 Fig. 2 Point distribution |
分别采用CIWOA算法及WOA算法对BP模型进行优化,优化后模型所取得的最佳适应度随迭代次数变化的收敛曲线如图 3所示。

|
图 3 收敛曲线 Fig. 3 Convergence curves |
由图 3分析可知, CIWOA-BP、WOA-BP两种模型收敛时迭代次数分别为24、34。相比于WOA-BP模型,CIWOA-BP模型收敛时所取得的最佳适应度更小,说明在收敛时CIWOA-BP模型相比WOA-BP模型的精度效果更好,由此可知CIWOA-BP模型的寻优能力更强、收敛速度更快。
3种模型拟合残差及外符合精度平均值结果如表 2所示。由表可知,BP模型最大拟合残差为3.14 cm, 外符合精度为2.09 cm, 拟合精度和稳定性均低于WOA-BP、CIWOA-BP模型。WOA-BP、CIWOA-BP模型最大拟合残差分别为1.72 cm和-1.18 cm, 最小拟合残差分别为0.78 cm和0.52 cm,外符合精度分别为1.24 cm和0.96 cm。
|
|
表 2 拟合结果 Tab. 2 Fitting results |
3种模型拟合残差波动曲线如图 4所示,其中CIWOA-BP模型的拟合残差在-1.18~1.03 cm区间波动,WOA-BP模型拟合残差在-1.27~1.72 cm区间波动,相比之下CIWOA-BP模型的精度和稳定性更好。
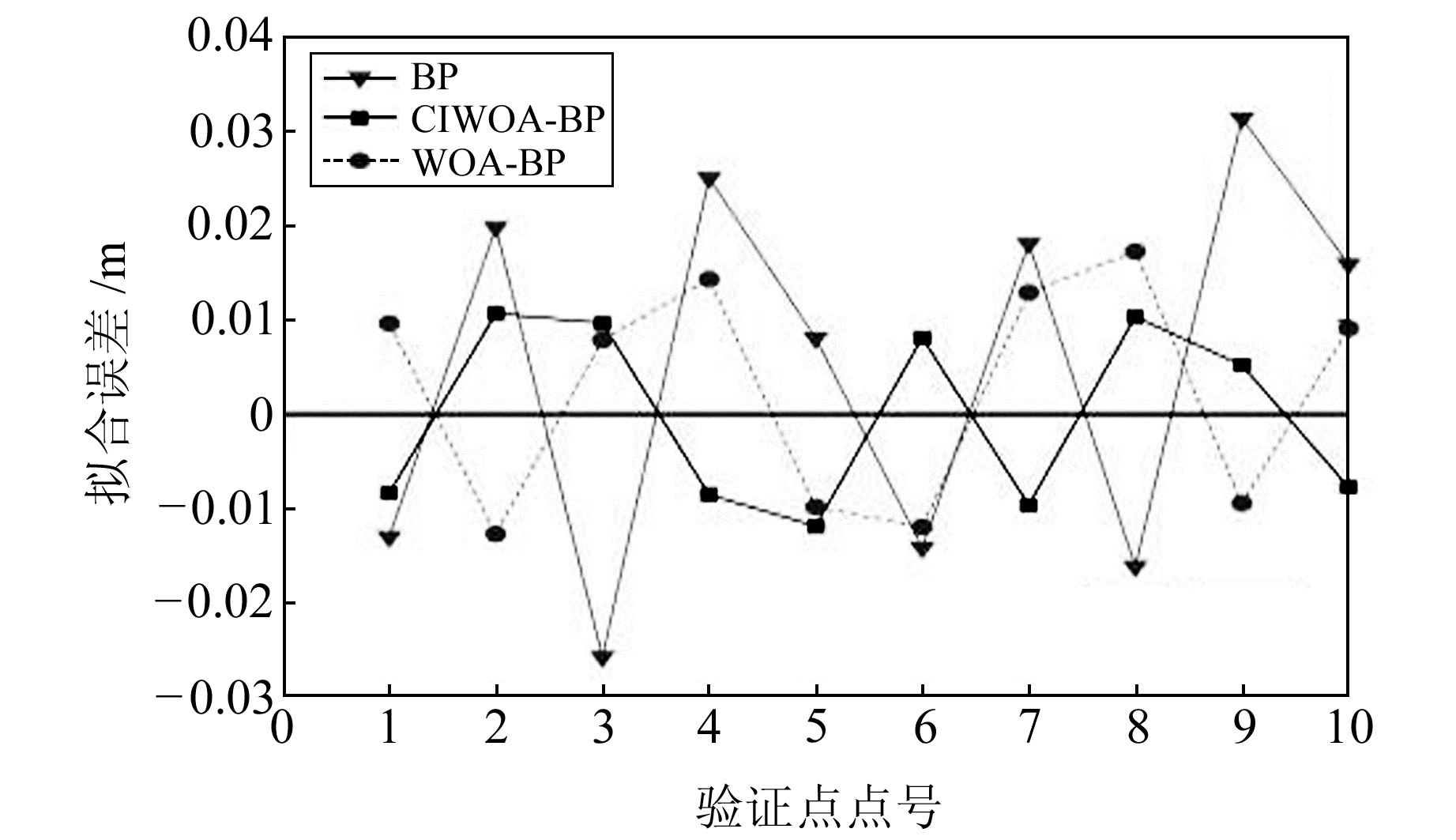
|
图 4 不同模型拟合残差 Fig. 4 Different model fitting residuals |
选取我国北部高原某矿区实测GPS控制网数据。该矿区覆盖面积约120 km2,测区内地形起伏较大,借此验证CIWOA-BP模型应对复杂地形时的精度和稳定性。采用测区内19个满足三等水准精度要求的GPS水准点,选取11个分布均匀的点作为建模点组,其余8个点作为验证点组。点位在测区分布情况如图 5所示。
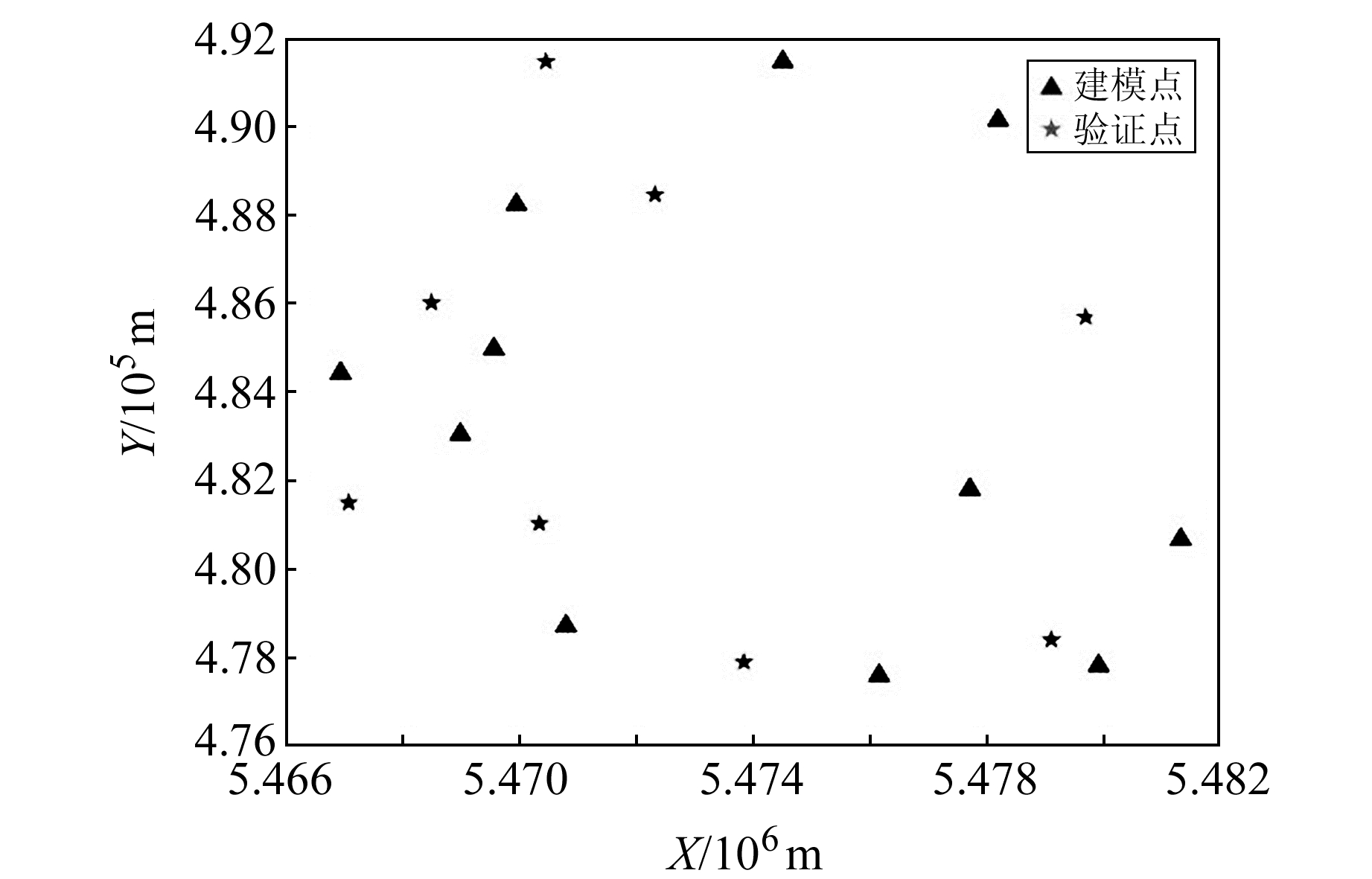
|
图 5 点位分布 Fig. 5 Point distribution |
结合表 3分析可知,当测区地形复杂、面积较大时BP模型的拟合残差效果最差,最大拟合残差为6.41cm,外符合精度为4.01 cm。CIWOA-BP模型和WOA-BP模型的最大拟合残差分别为-1.45 cm和-3.34 cm,外符合精度分别为1.12 cm和1.92 cm。CIWOA-BP模型的拟合精度和稳定性均高于WOA-BP模型。
|
|
表 3 各模型拟合结果 Tab. 3 Fitting results of each model |
从图 6可以看出,较BP模型,CIWOA-BP模型和WOA-BP模型的残差曲线波动更小,其中CIWOA-BP模型的拟合残差曲线波动最平稳,与实际值更接近,拟合效果最好。

|
图 6 不同模型拟合残差 Fig. 6 Different model fitting residuals |
本文采用改进的鲸鱼算法优化BP神经网络, 建立CIWOA-BP模型进行GPS高程异常拟合预测。加入BP、WOA-BP两种模型,并采取两组具有典型地形特征的工程实例数据进行对比实验。结果表明, CIWOA-BP模型与WOA-BP模型在沿海带状测区和高原内陆面状测区的拟合精度和稳定性均高于BP模型,其中CIWOA-BP模型的拟合精度最高、稳定性最好,验证了改进鲸鱼算法优化BP神经网络在应对不同地形GPS高程拟合问题中的有效性及适用性。
| [1] |
唐丽娟. GPS高程转换方法研究及精度分析[J]. 全球定位系统, 2017, 42(6): 88-91 (Tang Lijuan. Research Analysis of GPS Elevation Fitting Method[J]. GNSS World of China, 2017, 42(6): 88-91)
(  0) 0) |
| [2] |
王昶, 王旭. GPS高程拟合分区方法研究[J]. 大地测量与地球动力学, 2016, 36(1): 26-29 (Wang Chang, Wang Xu. Research on GPS Height Fitting Partition Method[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 26-29)
(  0) 0) |
| [3] |
王小辉, 王琪洁, 丁元兰, 等. 基于二次曲面和BP神经网络组合模型的GPS高程异常拟合[J]. 大地测量与地球动力学, 2012, 32(6): 103-105 (Wang Xiaohui, Wang Qijie, Ding Yuanlan, et al. Combined Model in Height Anomaly Fitting[J]. Journal of Geodesy and Geodynamics, 2012, 32(6): 103-105)
(  0) 0) |
| [4] |
Mirjalili S, Lewis A. The Whale Optimization Algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67 DOI:10.1016/j.advengsoft.2016.01.008
(  0) 0) |
| [5] |
刘威, 郭直清, 王东, 等. 改进鲸鱼算法及其在浅层神经网络搜索中的权值阈值优化[J]. 控制与决策, 2023, 38(4): 1 144-1 152 (Liu Wei, Guo Zhiqing, Wang Dong, et al. Improved Whale Optimization Algorithm and Its Weights and Thresholds Optimization in Shallow Neural Architecture Search[J]. Control and Decision, 2023, 38(4): 1 144-1 152)
(  0) 0) |
| [6] |
王坚浩, 张亮, 史超, 等. 基于混沌搜索策略的鲸鱼优化算法[J]. 控制与决策, 2019, 34(9): 1 893-1 900 (Wang Jianhao, Zhang Liang, Shi Chao, et al. Whale Optimization Algorithm Based on Chaotic Search Strategy[J]. Control and Decision, 2019, 34(9): 1 893-1 900)
(  0) 0) |
| [7] |
张晓莉, 王秦飞, 冀汶莉. 一种改进的自适应惯性权重的粒子群算法[J]. 微电子学与计算机, 2019, 36(3): 66-70 (Zhang Xiaoli, Wang Qinfei, Ji Wenli. An Improved Particle Swarm Optimization Algorithm for Adaptive Inertial Weights[J]. Microelectronics and Computer, 2019, 36(3): 66-70)
(  0) 0) |
| [8] |
魏宗海. 几种改进的BP神经网络在GPS高程拟合中的应用比较[J]. 全球定位系统, 2016, 41(5): 99-103 (Wei Zonghai. Comparison of Several Improved BP Neural Network in GPS Height Fitting[J]. GNSS World of China, 2016, 41(5): 99-103)
(  0) 0) |
| [9] |
蒙金龙, 唐诗华, 张炎, 等. 基于MVO优化神经网络的GNSS高程异常拟合方法[J]. 大地测量与地球动力学, 2022, 42(12): 1 233-1 238 (Meng Jinlong, Tang Shihua, Zhang Yan, et al. GNSS Height Anomaly Fitting Method Based on MVO Optimized Neural Network[J]. Journal of Geodesy and Geodynamics, 2022, 42(12): 1 233-1 238)
(  0) 0) |
| [10] |
杨天宇. 基于BP神经网络的GPS高程拟合及其在杭州湾跨海大桥中的应用[D]. 成都: 西南交通大学, 2006 (Yang Tianyu. GPS Height Fitting Based on BP Neural Network and Its Application in Hangzhou Bay Bridge[D]. Chengdu: Southwest Jiaotong University, 2006)
(  0) 0) |
2. Guoneng Baorixile Energy Co Ltd, 751 Shenbao Road, Hulun Buir 021599, China;
3. Jalainur Coal Industry Co Ltd, 17 Yulin Street, Hulun Buir 021410, China
 2024, Vol. 44
2024, Vol. 44

