多路径误差是GNSS高精度定位的重要误差源,可通过选择合适的观测站位置、改进接收机硬件设备、数据后处理建模方法进行抑制。通过数据后处理建模方式消弱多路径误差可以归纳为时间域和空间域两种。其中,时间域建模方法利用多路径时域周期重复性特点削弱多路径效应的影响,也被称为恒星日滤波;空间域建模方法包括格网法[1]、球谐函数法[2]等。应用恒星日滤波有两个关键的步骤:首先需建立多路径提取模型,广泛使用的有经验模态分解(EMD)[3]、小波滤波[4]、Vondrak滤波[5]、Kalman滤波[6]等技术;其次是确定多路径误差的重复时间(multipath repeat time,MRT)[7]。
针对BDS系统星座特性[8],本文提出一种正则化与恒星日滤波的多路径误差削减方法,基于重构后的载波相位单差残差,利用Tikhonov正则化提取多路径误差序列,对每颗BDS卫星分别进行多路径误差改正,在自举法的基础上进一步优化正则化参数,并通过实验验证该方法的正确性和有效性。
1 理论模型 1.1 单差残差重构在短基线载波相位差分定位过程中,经过站间、星间差分后,认为卫星轨道误差、卫星钟差、接收机钟差、电离层误差、对流层误差等可忽略不计。载波双差观测方程可表示为:
| $ \nabla \Delta \mathit{\Phi}_{\mathrm{rb}}^{\mathrm{jk}}=\nabla \Delta \rho_{\mathrm{rb}}^{\mathrm{jk}}+\lambda \nabla \Delta N_{\mathrm{rb}}^{\mathrm{jk}}+\nabla \Delta m+\nabla \Delta \varepsilon $ | (1) |
式中,
在静态短基线场景下,多路径误差具有周期特征,可以使用恒星日滤波对多路径误差进行改正。恒星日滤波方法采用双差残差的算法更为成熟,但使用双差的过程中需要解决参考卫星变化或丢失的问题;单差残差则没有这么多的限制,只涉及到站间差分的残差,并且在进行多路径改正时,只需参考自身卫星多路径的重复周期。
因此,在获取双差残差的基础上,采用Alber提出的“零均值”理论[9],求取单差残差:
| $ \mathit{\boldsymbol{Ds}}{{ = }}\mathit{\boldsymbol{d}} $ | (2) |
式中,D为系数矩阵,s为单差残差组成的向量,d为双差残差组成的向量。为保证矩阵D可逆,需要对单差残差附加额外的条件方程,即
| $ \begin{gathered} {\left[\begin{array}{ccccc} \omega_1 & \omega_2 & \omega_3 & \cdots & \omega_n \\ 1 & -1 & 0 & \cdots & 0 \\ 1 & 0 & -1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 0 & 0 & \cdots & -1 \end{array}\right]\left[\begin{array}{c} s_{\mathrm{rb}}^1 \\ s_{\mathrm{rb}}^2 \\ s_{\mathrm{rb}}^3 \\ \vdots \\ s_{\mathrm{rb}}^n \end{array}\right]=} \\ {\left[\begin{array}{c} \sum \omega_i s_{\mathrm{rb}}^i \\ s_{\mathrm{rb}}^1-s_{\mathrm{rb}}^2 \\ s_{\mathrm{rb}}^1-s_{\mathrm{rb}}^3 \\ \vdots \\ s_{\mathrm{rb}}^1-s_{\mathrm{rb}}^n \end{array}\right]=\left[\begin{array}{c} 0 \\ d_{\mathrm{rb}}^{12} \\ d_{\mathrm{rb}}^{13} \\ \vdots \\ d_{\mathrm{rb}}^{1 n} \end{array}\right]} \end{gathered} $ | (3) |
式中,ωi为基准站、流动站上卫星i的权重系数。通常认为,多路径误差的大小受卫星高度角的影响,权重系数ωi由卫星i的高度角来确定,即可用ωi=sin2(θ)定权。
1.2 Tikhonov正则化建模 1.2.1 Tikhonov正则化建模提取多路径由前文可知,转换后的单差残差即为多路径建模的原始数据,由多路径误差m和观测噪声ε组成。可以表示为:
| $ \varphi_i=m_i+\varepsilon_i, i=1, 2, \cdots, n $ | (4) |
式中,下标i为观测历元,φi为转换后的单差残差序列,mi为需要提取的多路径序列,εi为观测噪声。为分离多路径序列mi,构造正则化目标函数:
| $ \begin{gathered} J\left(m_i\right)= \\ \sum\limits_{i=1}^n \omega_i\left(\varphi_i-m_i\right)^2+\alpha \sum\limits_{i=1}^{n-1}\left(m_{i+1}-m_i\right)^2 \end{gathered} $ | (5) |
式中,ωi为由卫星高度角确定的权重系数,α为正则化参数。式(5)为Tikhonov正则化一阶差分模型,相关文献对不同形式的目标函数进行了探讨[10],其结果没有明显区别。本文仅利用一阶差分模型,因此式(5)可用矩阵形式表示为:
| $ \boldsymbol{J}=(\boldsymbol{\varphi}-\boldsymbol{m})^{\mathrm{T}} \boldsymbol{W}(\boldsymbol{\varphi}-\boldsymbol{m})+\alpha \boldsymbol{m}^{\mathrm{T}} \boldsymbol{R} \boldsymbol{m} $ | (6) |
式中,W为权阵,W=diag(ω1, ω2, …, ωn),R为正则化矩阵,m为多路径误差。
要得到式(6)中的多路径序列,其极值需满足的必要条件可表示为:
| $ (\boldsymbol{W}+\alpha \boldsymbol{R}) \hat{\boldsymbol{m}}=\boldsymbol{W} \boldsymbol{\varphi} $ | (7) |
式中,
正则化矩阵采用选取相邻两个多路径误差之差的平方和确定,即
| $ \boldsymbol{m}^{\mathrm{T}} \boldsymbol{R} \boldsymbol{m}=\sum\limits_{i=1}^{n-1}\left(m_{i+1}-m_i\right)^2 $ | (8) |
则有:
| $ \boldsymbol{R}=\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G} $ | (9) |
其中,
通过式(7)可以估计出相应的多路径序列。而在实际处理过程中,通常采用高斯消元法等矩阵分解算法提高数据处理效率。
1.2.3 正则化参数α的确定正则化参数α用来调节残差与约束项之间的平衡,参数值的选取对解的优劣性是敏感的,因此选择合适的正则化参数显得尤为重要。采用自举法(bootstrap)对多路径建模误差进行评估,来获得正则化参数[11]。候选正则化参数的集合为α={0.1, 1, 10, 50, 100, …},对于集合中的每个正则化参数,通过式(7)分别确定其对应的多路径序列。定义以下归一化残差(载波相位单差残差的残差)为:
| $ \eta_i=\omega_i\left(\varphi_i-\hat{m}_i\right), i=1, 2, \cdots, n $ | (10) |
式中,
从归一化残差序列ηi中有放回地抽样,得到新的序列
| $ \hat{m}(\alpha)=\frac{1}{B+1} \sum\limits_{b=0}^B \hat{m}_b(\alpha) $ | (11) |
当b=0时,φ为原始载波相位单差残差。定义误差统计方法为:
| $ \begin{aligned} E(\alpha)= & \frac{1}{n B} \sum\limits_{b=0}^B\left[\hat{m}_b(\alpha)-\hat{m}(\alpha)\right]^{\mathrm{T}} \\ & {\left[\hat{m}_b(\alpha)-\hat{m}(\alpha)\right] } \end{aligned} $ | (12) |
正则化参数确定为:
| $ \hat{\alpha}=\operatorname{argmin} E(\alpha), \alpha \in\{0.1, 1, 10, 50, 100, \cdots\} $ | (13) |
为进一步优化正则化参数,本文提出一种循环选取正则化参数的方法(circle-bootstrap)。具体计算流程为:
1) 采用自举法选取正则化参数
2) 代入公式(7),计算对应的多路径误差
3) 循环计算以0.1
4) 重复步骤2),计算每个αi值对应的多路径误差
5) 输出min{E(αi)}对应的正则化参数αopt。
2 数据处理与分析为验证北斗卫星轨道周期和多路径周期的一致性及正则化方法的可行性,计算单差残差并提取每颗卫星的多路径模型,对基线结果进行评估。本文使用Curtin大学CUT0、CUTC站采集的观测数据,测站距离7.99 m,接收机型号为TRIMBLE NETR9,时间为2022-08-19~26(doy231~238),采样间隔为30 s,截止高度角设置为10°。利用GNSS数据处理软件RTKLIB和MATLAB平台实现本文方法。
在北斗卫星导航定位系统中,由于GEO与IGSO卫星独特的地球同步运行方式,致使其运行轨迹在相邻2 d具有较好的重复性,这两类卫星对应的轨道重复周期约为1个恒星日;MEO卫星的运行轨迹在相邻2 d内没有重复,而在间隔7 d后,此类卫星的运行轨迹却存在着较强的相关性,所以MEO卫星对应的轨道重复周期约为7个恒星日。图 1展示了部分卫星在前后2个周期(doy237~238、doy231~238)的载波相位残差,可以看出,对于GEO与IGSO卫星在doy237和doy238的载波相位单差残差具有极大的相似性,这种相似性表现为相同卫星在相邻2 d同一观测时段内,第2天的单差残差曲线以一定的时间提前量,与该卫星在第1天的单差残差曲线表现出重复性。同样,MEO卫星在doy231和doy238的载波相位单差残差具有极大的相似性,但所对应的时间提前量明显与GEO与IGSO卫星存在差异。

|
图 1 部分卫星在前后2个周期(doy237~238、doy231~238)的载波相位单差残差 Fig. 1 Residual of carrier phase single difference at doy237-238 and doy231-238 for partial satellites |
恒星日滤波的关键之一是准确估计多路径重复时间。本文在轨道重复时间法(ORTM)基础上,根据广播星历将1 d分为24个时段,利用每h的轨道参数分段估计多路径误差的重复时间(multipath repeat time,MRT),分段改正。图 2展示了所有卫星对应的平均MRT和各时段对应的MRT估计值可以看出,GEO和IGSO卫星单差残差在相应周期内对应的多路径误差重复时间各不相同,平均MRT约为239 s;每h分段的最大MRT出现在C02卫星处,达到258 s,差值为19 s。对于MEO卫星来说,在相应周期内,此类卫星的单差残差对应的平均MRT约为1 698 s;每h分段的最大MRT出现在C24卫星处,达到1 709 s,差值为11 s。因此,仅利用平均MRT并不能完全适应每个时段,这就体现出利用分段思想估计MRT的优越性。

|
图 2 所有卫星对应的平均和分段多路径误差重复时间 Fig. 2 Mean MRT estimates and hourly MRT estimates for all satellites |
在正则化提取过程中,由于在目标函数里加入了平方残差项,在本质上对异常值不是鲁棒的。因此采用三次样条插值对单差残差进行预插值,以替换异常值和填充缺失的数据值,为后续提取多路径提供高质量的数据。本文将利用自举法选取正则化参数的方法记作TB方法,利用循环选取正则化参数的方法记作TC方法。图 3展示了C01(左)、C07(中)于doy237,C28(右)于doy231利用TB(图 3(a))、TC(图 3(b))和小波滤波(图 3(c))方法提取的多路径误差。从图 3(a)和3(b)可以看出,通过Tikhonov正则化方法提取多路径信号是正确可行的,多路径信号比原始载波相位单差残差更具平滑性。利用TC方法提取的多路径误差略优于TB方法,即在利用Tikhonov正则化方法提取多路径误差时,应尽可能地获取最优正则化参数,其结果更准确。

|
图 3 C01、C07于doy237,C28于doy231利用TB、TC和小波滤波方法提取的多路径误差 Fig. 3 Multipath error extracted by C01, C07 at doy237, C28 at doy231 using TB, TC and wavelet filtering method |
为体现方法的有效性,同时采用小波滤波方法进行数据分析,直观地比较本文方法的相对性能。所选小波基函数为sym6,分解级数为4,滤波阈值使用MATLAB提供的默认阈值。从图 3(b)和3(c)可知,本文方法的去噪效果较好,提取的系统性多路径误差与残差波动性一致,具有较好的保真度。同时,与经典的小波滤波相比,该方法提取的多路径误差曲线与小波滤波近似,滤波前后的载波相位残差改善效果比小波滤波更优。
经上述过程后,就完成了恒星日滤波的2个关键步骤,即重复时间的计算和多路径误差的提取。因此,能够将上一周期数据应用到当前周期,利用计算得到的时间提前量,从当前周期中减去前一周期建立的多路径误差。图 4展示了doy238对C04(左)、C06(中)、C19(右)应用TB、TC和小波滤波方法的恒星日滤波前后载波相位的SD残差。由图 4(a)和4(b)可以观察到,多路径误差得到有效抑制,滤波后的后验单差残差已经剔除原始单差残差中的系统误差,表现出随机特性,效果较好的部分接近于白噪声。从图 4(b)和4(c)中可以看出,正则化方法的效果略优于小波方法,进一步验证了本文方法的有效性。

|
图 4 C04、C06和C19于doy238应用TB、TC和小波滤波方法恒星日滤波前后的载波相位SD残差 Fig. 4 Carrier phase SD residual of C04, C06 and C19 before and after sidereal filtering by applying TB, TC and wavelet filtering method on doy238 |
doy238恒星日滤波缓解多路径误差前后载波相位单差残差的均方根和改进量如图 5所示,可以看出,所有可见卫星对TB、TC和小波滤波的平均改进百分比分别为33.9%、40.5%和32.6%。鉴于BDS独特的星座特性,分别统计每类卫星的改进量:对于GEO卫星,采用TB、TC和小波滤波方法,平均改进量分别为37.9%、45.9%、36.7%;对于IGSO卫星,采用3种方法的平均改进量依次为30.5%、38.2%、26.4%;对于MEO卫星,采用3种方法平均改进33.3%、37.5%、34.5%。由此可以得出,采用TC方法应用恒星日滤波后,改进效果最佳。另外,对于GEO卫星的多路径改进的效果较其他两类卫星更为显著。
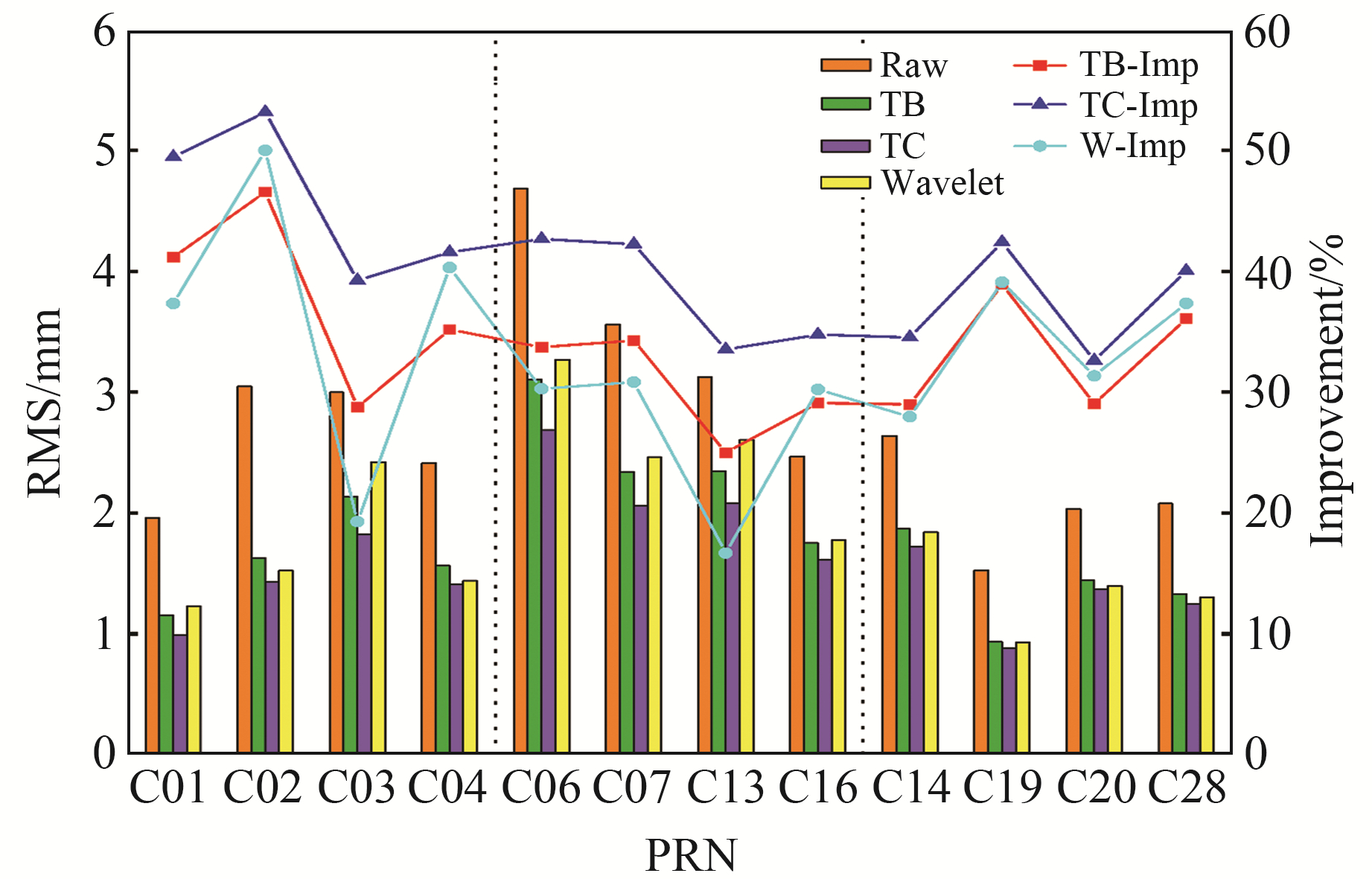
|
图 5 doy238恒星日滤波前后载波相位单差残差的均方根和改进量 Fig. 5 RMS and improvement of carrier phase SD residual before and after sidereal filtering on doy238 |
多路径缓解后模糊度固定成功率的提高将进一步证明本文方法的优越性。doy238多路径误差改进前后的模糊度固定成功率如表 1所示,经过恒星日滤波多路径缓解后,TB、TC和小波滤波方法的模糊度固定成功率分别提高7.9%、8.2%、8.1%。
|
|
表 1 doy238多路径误差改正前后模糊度固定成功率对比 Tab. 1 Comparison of success rate of ambiguity fixing before and after multipath error correction on doy238 |
doy238多路径误差改正前后均方根如表 2所示,可以看出,N、U方向定位精度较E方向高,定位结果较优。3种方法改正效果都非常显著,经过TB、TC和小波滤波后,E、N、U方向改进分别为23%、26.3%、41.7%,24.8%、26.3%、42.7%和22.4%、23.7%、41.7%。总体上TC方法的多路径误差改正效果更优。
|
|
表 2 doy238多路径误差改正前后均方根对比 Tab. 2 Comparison of RMS before and after multipath error correction on doy238 |
在静态或准静态场景中,多路径误差在某种程度上是具有系统性的,而不纯粹是随机的,应该将其视为一种信号,而非噪声。基于这一事实,可以借助重复性特征对其进行经验性建模。本文针对北斗卫星独特的运行方式,基于重构后的载波相位单差残差,利用Tikhonov正则化提取多路径误差序列,对每颗BDS卫星分别进行多路径误差改正,进一步优化正则化参数,并通过实验验证该方法的正确性和有效性。准确估计多路径重复时间是恒星日滤波的关键步骤之一。利用每h轨道参数分段估计的多路径误差重复时间略优于ORTM方法。利用Tikhonov正则化方法正确提取多路径信号是可行的,多路径误差与原始残差相比更具平滑性,并且利用TC方法提取的多路径误差要优于TB方法,这意味着应用Tikhonov正则化方法时,应尽可能估计出最优正则化参数。对于载波相位单差残差,采用本文方法后,所有可见卫星在第2天的RMS平均提高40.5%;坐标残差E、N、U方向分别提高24.8%、26.3%和42.7%。
| [1] |
Dong D, Wang M, Chen W, et al. Mitigation of Multipath Effect in GNSS Short Baseline Positioning by the Multipath Hemispherical Map[J]. Journal of Geodesy, 2016, 90(3): 255-262 DOI:10.1007/s00190-015-0870-9
(  0) 0) |
| [2] |
Guo J Y, Li G W, Kong Q L, et al. Modeling GPS Multipath Effect Based on Spherical Cap Harmonic Analysis[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(6): 1 874-1 879 DOI:10.1016/S1003-6326(14)63266-0
(  0) 0) |
| [3] |
罗飞雪, 戴吾蛟, 伍锡锈. 基于交叉证认的EMD滤波及其在GPS多路径效应中的应用[J]. 武汉大学学报: 信息科学版, 2012, 37(4): 450-453 (Luo Feixue, Dai Wujiao, Wu Xixiu. EMD Filtering Based on Cross-Validation and Its Application in GPS Multipath[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 450-453)
(  0) 0) |
| [4] |
Xiong Y L, Huang D F, Shun C K. GPS Phase Measure Cycle-Slip Detecting and GPS Baseline Resolution Based on Wavelet Transform[J]. Survey Review, 2003, 37(289): 200-207 DOI:10.1179/sre.2003.37.289.200
(  0) 0) |
| [5] |
Ping Z. Separation of Structural Vibrations and GPS Multipath Signals Using Vondrak Filter[J]. Journal of Central South University(Science and Technology), 2006, 37(6): 1 189-1 195
(  0) 0) |
| [6] |
戴吾蛟, 伍锡锈, 罗飞雪. 一种利用增广参数Kalman滤波的GPS多路径效应处理方法[J]. 武汉大学学报: 信息科学版, 2012, 37(4): 423-427 (Dai Wujiao, Wu Xixiu, Luo Feixue. GPS Multipath Effect Processing Method Based on Augmented Parameters Kalman Filtering[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 423-427)
(  0) 0) |
| [7] |
Wang M H, Wang J X, Dong D N, et al. Comparison of Three Methods for Estimating GPS Multipath Repeat Time[J]. Remote Sensing, 2018, 10(2)
(  0) 0) |
| [8] |
Ye S R, Chen D Z, Liu Y Y, et al. Carrier Phase Multipath Mitigation for Beidou Navigation Satellite System[J]. GPS Solutions, 2015, 19(4): 545-557 DOI:10.1007/s10291-014-0409-1
(  0) 0) |
| [9] |
Alber C, Ware R, Rocken C, et al. Obtaining Single Path Phase Delays from GPS Double Differences[J]. Geophysical Research Letters, 2000, 27(17): 2 661-2 664 DOI:10.1029/2000GL011525
(  0) 0) |
| [10] |
Chang G B, Chen C, Yang Y X, et al. Tikhonov Regularization Based Modeling and Sidereal Filtering Mitigation of GNSS Multipath Errors[J]. Remote Sensing, 2018, 10(11)
(  0) 0) |
| [11] |
Efron B, Tibshirani R J. An Introduction to the Bootstrap[M]. New York: Chapman and Hall, 1993
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44


