2. 中国测绘科学研究院,北京市莲花池西路28号,100036
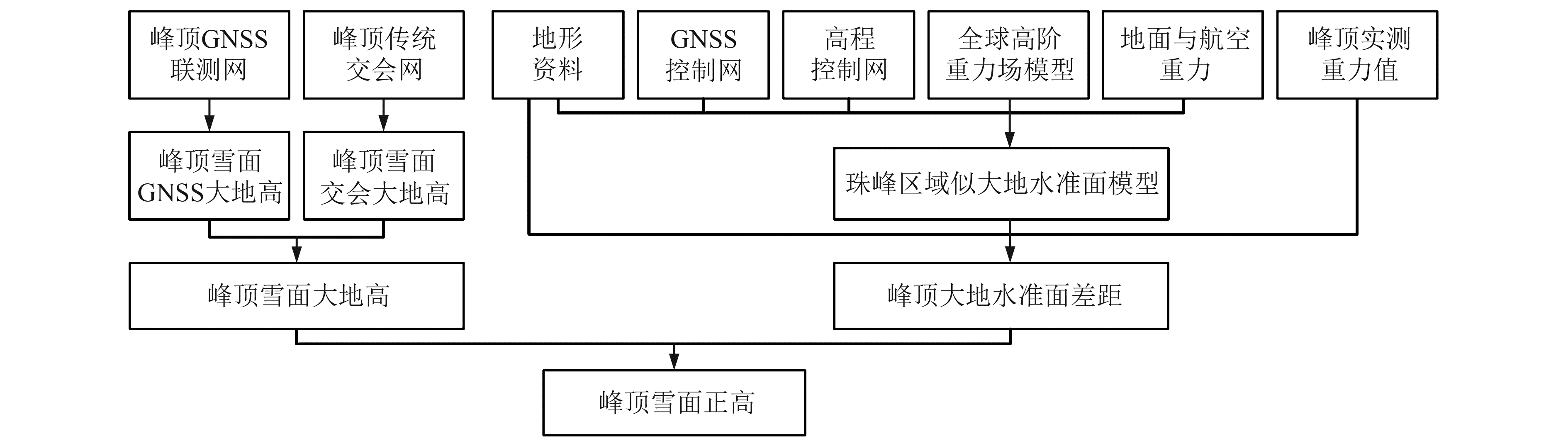
珠穆朗玛峰(简称珠峰)位于中尼边境,是地球最高峰。国内外学者曾多次对珠峰高程进行测量:陈俊勇等[2-3]及郭春喜等[4-5]曾对2005年中国珠峰测高大地测量数据的获取和数据处理进行详细介绍;张江齐等[6]及柳建乔[7]对珠峰测量历史进行详细的研究与综述,介绍了2019年以前历次珠峰测量的方案、设备及最终产出的成果;张赤军[8]围绕珠峰高程精度、雪层厚度、大地水准面精度、地壳垂直运动及如何将似大地水准面转换到大地水准面等进行研究后认为,采用正常高加转换公式中的重力或地形资料求取珠峰正高(海拔高)较为合适;党亚民等[9-10]对2020年珠峰高程测量的整个技术流程进行了阐述,但并未对数据处理流程作详细解析。基于此,本文着重介绍2020年珠峰高程测量数据处理过程中资料的使用情况、详细的数据处理技术流程(图 1)和中尼联合发布的2020年珠峰高程成果,并总结2020年珠峰高程测量数据处理成果特点,阐述其可靠性与精度。
|
图 1 2020年珠峰高程测量数据处理整体流程 Fig. 1 The data processing flow chart of 2020 mount Qomolangma height measurement |
GNSS网包括以下4种观测数据:
1) 基准站网:选取西藏、新疆、青海3省范围内较为稳定的105个国家GNSS基准站(含2个IGS站)[9]、10个尼泊尔境内GNSS基准站、2个临时基准站,共计117个站点形成珠峰地区GNSS基准站网。
2) 地壳运动监测网:珠峰高程测量地壳运动监测网共观测21个B级GNSS站点,每个站点观测3个时段,长约24 h。观测数据含GPS、北斗2种观测信号。
3) 局部控制网:珠峰高程测量局部控制网共观测61个C级GNSS站点,每个站点观测1~2个时段,长约8~14 h。观测数据含GPS、北斗2种观测信号。
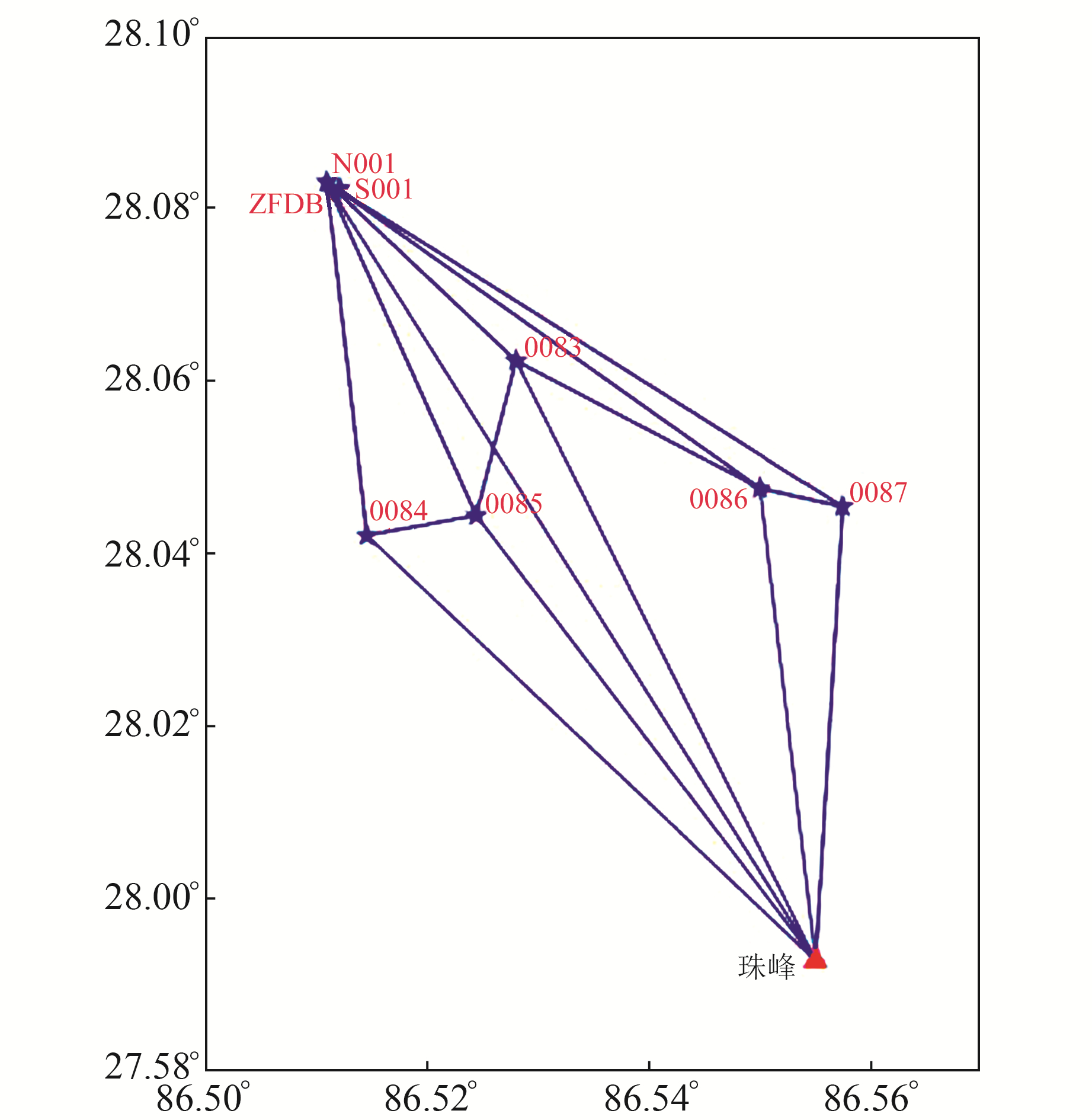
4) 峰顶联测网:珠峰高程测量峰顶联测网共计10个点,包括峰顶1个点、5个交会点、2个大本营微网点及2个临时基准站,采样间隔为1 s。其中,峰顶点采用国产与进口2台设备同时观测,观测数据含GPS、北斗2种观测信号,点位分布见图 2。
|
图 2 峰顶GNSS联测网点位分布 Fig. 2 Distribution of summit GNSS network points |
珠峰高程测量高程控制网包括3个等级的水准路线、测距高程导线和跨河水准路线,其中一等水准路线3条,共520.0 km;二等水准路线5条,共253.1 km;三等水准路线5条,共8.6 km。采用电磁波测距高程导线的方法完成几何水准测量中的困难点位高程传递,包括垂直角与距离测量,共计18.5 km[9];采用测距三角高程法完成中绒和西绒两交会点共计3.4 km的跨河水准测量。
1.3 峰顶交会网2020-05-27成功在峰顶竖立测量觇标后,分别从大本营、Ⅲ7、西绒、中绒、东绒2、东绒3六个交会点对峰顶觇标进行交会观测,测量水平角、垂直角和距离[9]。同时,在2020-05-27~29进行珠峰交会测量时,每日07:00~21:00在海拔高度为4 301.2 m的西藏日喀则市定日县探空站每隔2 h施放一组探空气球,气球每上升100 m测定1次气象数据[11],如气温、气压、相对湿度等。
1.4 重力观测 1.4.1 绝对重力点选择日喀则(ZF01)、珠峰(ZF04)2个点,其点位与日喀则(XZRK)、珠峰(ZF04)2个连续运行基准站并址,联测二等水准。
1.4.2 加密重力网对水准路线和登山路线上1个基本点、5个二等重力点、202个加密重力点进行测量,点位分布见图 3。

|
图 3 珠峰地区新测重力点分布 Fig. 3 Distribution of new ground gravity point in the area of mount Qomolangma |
首次在珠峰地区开展航空重力测量[9],其中有39条EW向数据测线、9条NS向交叉测线,测线间距为5 km。成果共计83 803点,其中测线数据58 992点、控制数据25 811点,测线点平均航高约10 250 m,数据采样率为2 Hz。
1.4.4 收集重力资料为提高珠峰地区实测重力数据的分辨率,收集9 319个重力点成果,其中国外重力点1 232个、国内重力点8 087个,包括中尼重力剖面成果及我国历年在珠峰地区观测的重力成果等。
1.5 天文观测于2020-04-24、2020-05-09分别完成大本营、东绒2两个交会点的天文观测,获得其天文经纬度。同时,从国家测绘档案资料馆大地测量档案分馆收集珠峰地区8个往期实测天文点成果。
1.6 地形资料收集珠峰地区1 ∶50 000分幅的全球测图数据1 173幅、国家西部1 ∶50 000地形图空白区测图工程数据1 132幅和整个珠峰地区的SRTM3数据(航天雷达测绘任务获得的地形数据),将3种数据分别与珠峰测区的加密重力测量数据进行匹配性分析,并结合生产3种数字地形模型时的资料来源、生产方式、生产工艺,最终确定采用国家西部1 ∶50 000地形图空白区测图工程数据和SRTM3数据生成的珠峰地区3″×3″、30″×30″、1.5′×1.5′分辨率的地形数据。
2 峰顶雪面大地坐标计算为获得峰顶雪面大地坐标,同时进行GNSS和传统三角网的外业观测,数据处理时将2种观测数据分别计算得到的大地坐标加权平均,获得最终成果。
2.1 峰顶GNSS联测网峰顶GNSS联测网解算时选取峰顶联测的同步交会点与1个大本营临时基准站作为峰顶GNSS联测网的起算点,求解峰顶坐标。
数据处理基本思路为:首先利用GNSS观测数据分别获取峰顶不同设备(国产设备与进口设备)的GPS与北斗系统坐标;然后依据点位中误差,采用基于结果融合的方法获得2套设备的单卫星导航定位系统(GPS与北斗)融合结果,将GPS与北斗的单卫星导航定位系统结果进行融合,最终获得峰顶大地坐标。
2.2 峰顶传统三角网 2.2.1 探空气球气象数据整理与处理从每组探空气球记录的原始探空气象数据中提取几个时间段的距地高度、气温、气压、相对湿度、施放时间等要素信息,整理形成探空气象数据文件,计算大气气温、气压的垂直梯度,为计算各测站的大气垂直折光系数K值提供参考,也为用光电测距方法测定测站与珠峰顶的距离提供气象改正数据。
2.2.2 交会点垂线偏差计算垂线偏差主要用于对传统测量方法获取的观测值进行归算。首先采用珠峰地区1.5′×1.5′格网重力异常数据作为地面重力垂线偏差计算的输入数据,采用国内外广泛应用的移去-恢复技术和先进的高阶次地球重力位模型EIGEN-6C4完成珠峰附近大地点地面重力垂线偏差的计算;然后采用珠峰附近实测天文大地点基于参考椭球的垂线偏差对地面重力垂线偏差进行系统改正,获得珠峰附近大地点相应于参考椭球的地面垂线偏差。
2.2.3 边角网确定峰顶大地坐标通过边角网间接平差法,将归算到参考椭球面上的方向和边长值作为观测元素,计算珠峰峰顶在参考椭球面上的大地坐标[11]。
2.2.4 三角高程网确定大地高基于6个交会点至珠峰的观测垂直角,利用6个交会点和珠峰平面坐标反算大地线长度,考虑大地折光与地球曲率的影响,采用严密的三角高程计算公式,推算6点至珠峰的大地高差,计算基于不同交会点的峰顶大地高,对6个峰顶大地高加权平均获得最终成果。
2.3 峰顶雪面大地坐标综合确定对GNSS技术和交会观测技术计算的珠峰峰顶雪面大地坐标按照各自成果精度定权,并采用加权平均法综合确定最终成果,详情见表 1。
|
|
表 1 峰顶大地坐标成果精度统计 Tab. 1 Statistic of precision for summit's geodetic coordinates |
充分利用各类观测数据与收集的资料,基于地球物理理论与算法,计算得到珠峰峰顶1985国家高程基准大地水准面差距及全球高程基准大地水准面差距。
3.1 GNSS网解算按照分级解算、逐级控制的原则,逐一解算基准站网、地壳运动监测网、局部控制网的ITRF2014参考框架、瞬时历元坐标,结果见表 2(单位mm)。其中,地壳运动监测网、局部控制网需采用GPS、北斗2类导航定位观测数据分别进行数据处理,并将计算结果进行融合,获得最终成果。
|
|
表 2 各级GNSS网成果精度统计 Tab. 2 Statistic of precision for GNSS network results |
按照分级解算、逐级控制的原则,逐一解算各等级水准数据。一等水准利用“国家现代测绘基准数据处理国家高程控制网成果表”的“日喀则基岩点北”作为起算点,该点已经过检测且合限;二等水准利用此次一等水准测量成果作为起算;三等水准利用此次一、二等水准测量成果作为起算;测距高程导线及跨河水准测量利用此次二、三等水准测量成果作为起算。采用结点平差法,基于测站定权列误差方程,以经过各项改正后的高差均值为元素,以待定结点高程为未知数。平差计算完成后,按照附合路线平差的方法推出其他各水准点的高程,直接基于起算点高程和经过各项高差改正数校正后的往返测高差中数推算待定点高程。
3.3 GNSS水准点匹配基于GNSS控制网和高程控制网成果,共匹配到珠峰地区61个GNSS水准点,采用最小二乘配置法对重力似大地水准面进行初步拟合纠正,检验GNSS水准点的可靠性,避免粗差数据对似大地水准面产生畸变等不良影响。经计算分析未发现异常点,61个GNSS水准点分布见图 4。利用GNSS水准点可以将重力似大地水准面拟合适配于我国1985年国家高程基准,根据2020年珠峰高程测量中尼双方多次谈判后达成的协议,仅公布基于全球高程基准的珠峰海拔高,本文不再介绍基于1985年国家高程基准的珠峰海拔高。

|
图 4 珠峰地区GNSS水准点分布 Fig. 4 Distribution of GNSS-leveling points in the area of mount Qomolangma |
1) 绝对重力。包含日喀则(ZF01)和珠峰(ZF04)2个绝对重力点。数据处理时,点位大地坐标采用连续运行的基准站坐标成果,高程采用二等水准联测成果,极移改正数采用IERS公布的最终值。绝对重力值计算过程包括固体潮改正、海潮负荷改正、气压改正、极移改正、光速改正及高度改正。对每组重力值求平均获取组平均重力值,对组平均重力值求平均获取总平均重力值,计算墩面和距离墩面高1.3 m处的重力值。
2) 加密重力。数据处理时,首先将绝对重力点作为起算,对高等级的基本点、二等点重力测量进行数据处理;然后将绝对重力点和高等级点作为起算对加密重力测量进行数据处理。数据处理时加入的改正项包括固体潮改正、气压改正、仪器高改正、零漂改正、比例因子改正等。
3.4.2 航空重力航空重力原始数据为空中离散点上经调平后的重力加速度值、大地高值及点位大地坐标等,测线数据按5 s进行抽稀后参加航空重力的数据处理。基于对原始数据的参数分析及多种延拓方法的试算分析,并遵循尽量减少边缘效应导致的信息量损失、确保充分发挥珠峰地区航空重力数据作用的原则,最终采用梯度延拓法实现航空重力数据向地面的解析延拓,得到地面重力异常值。
3.5 珠峰地区重力似大地水准面确定利用珠峰区域及周边的地面与航空重力成果、数字高程模型,采用Molodensky公式及EGM2008、EIGEN-6C4、XGM2019e_2159[12-13]参考重力场模型,计算各模型不同积分半径的区域重力似大地水准面。利用GNSS水准点实测似大地水准面,对基于不同参考重力场模型和积分半径构建的重力似大地水准面进行精度评定,经反复分析比较,最终选定采用EIGEN-6C4、积分半径为57 km计算的重力似大地水准面,其检核精度为±4.8 cm。基于该重力似大地水准面,采用双线性内插法得到峰顶似大地水准面差距。
3.6 峰顶大地水准面与似大地水准面之间的距离计算珠峰峰顶雪面正常高HQr与正高(海拔高)HQg的换算公式为:
| $ H_Q^g=\frac{\gamma_m}{g_m} H_Q^r $ | (1) |
式中,γm、gm分别为沿正常重力场力线上各点的正常重力和实测重力的平均值。计算中考虑到力线上重力值的非线性变化,将海水面至珠峰峰顶端分为n个分点,综合利用峰顶实测重力值和周边重力与地形资料,采用移去-恢复技术,经严密计算得到γm和gm值,再结合基于珠峰地区重力似大地水准面得到的峰顶正常高,计算得到峰顶正高。将正高与正常高作差,得到峰顶大地水准面与似大地水准面之间的距离。
3.7 基于IHRS峰顶大地水准面的差距计算依据国际大地测量协会2015年在捷克布拉格发布的关于国际高程参考系统(IHRS)[14-15]的定义和官方决议,采用IHRS定义的重力位值和本次采用的参考椭球建立珠峰地区重力大地水准面模型,计算得到珠峰峰顶的大地水准面差距,作为IHRS基准的珠峰海拔高起算基准[9]。
基于IHRS的峰顶大地水准面差距主要通过计算大地水准面差距的零阶项实现,需要考虑IHRS全球高程基准在峰顶的重力位W0与本次采用的参考椭球正常重力位U0及不同基准的地心引力常数的差异。计算公式如下:
| $ N_0=\frac{\left(G M-G M_0\right)}{r_{p_0} \cdot \gamma_{Q_0}}-\frac{W_0-U_0}{\gamma_{Q_0}} $ | (2) |
式中,N0为大地水准面差距的零阶项,GM为IHRS定义的地心引力常数,GM0为GRS80参考椭球的地心引力常数,W0为IHRS定义的重力位值,U0为GRS80参考椭球的正常重力位,rp0为大地水准面上相应点的地心距离,γQ0为椭球面上相应点的正常重力值。
基于IHRS的峰顶大地水准面差距N为:
| $ N=\zeta+\Delta+N_0 $ | (3) |
式中,ζ为峰顶高程异常。
4 结语根据峰顶雪面大地高、峰顶基于IHRS的大地水准面差距,中尼共同宣布珠峰基于IHRS的珠峰峰顶雪面海拔高(正高)为8 848.86 m。
2020年珠峰高程测量数据处理成果特点有:
1) 大地水准面精度由2005年的14.6 cm提高到2020年的4.8 cm,其中航空重力数据的引入使大地水准面精度提升约40%;峰顶实测重力值显著提升了峰顶大地水准面差距的可靠性。
2) 峰顶雪面大地高北斗成果与GPS成果精度相当,高程方向精度约为±2 cm,融合后精度提升至±0.9 cm,2005年高程方向精度约为±3 cm,本次峰顶雪面大地高精度大幅度提升。
3) 高精度、高可靠性国产仪器的使用及更加可靠的气象数据共同提升了峰顶三角高程网成果与GNSS成果的一致性,二者在高程方向上的差异由29 cm缩小至2.6 cm。
4) 中尼首次构建全球高程基准,两国全球高程基准符合性较好,为两国共同构建一致的全球高程基准奠定了坚实的基础。
| [1] |
常吉庆. 历次珠峰高程测量情况简介[J]. 测绘通报, 2005(10): 2-6 (Chang Jiqing. An Introduction to All Previous Measurements of Height of Mount Qomolangma[J]. Bulletin of Surveying and Mapping, 2005(10): 2-6)
(  0) 0) |
| [2] |
陈俊勇, 庞尚益, 张骥, 等. 对我国35年来珠峰高程测定成果的思考[J]. 测绘学报, 2001, 30(1): 1-5 (Chen Junyong, Pang Shangyi, Zhang Ji, et al. The Height Determination of Qomolangma Peak in China: Review and Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 1-5)
(  0) 0) |
| [3] |
陈俊勇, 张燕平, 岳建利, 等. 2005珠峰高程测定[J]. 测绘学报, 2006, 35(1): 1-3 (Chen Junyong, Zhang yanping, Yue jianli, et al. 2005 Height Determination of Qomolangma[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 1-3)
(  0) 0) |
| [4] |
郭春喜, 宁津生, 陈俊勇, 等. 珠峰地区似大地水准面精化与珠峰顶正高的确定[J]. 地球物理学报, 2008, 51(1): 101-107 (Guo Chunxi, Ning Jinsheng, Chen Junyong, et al. Improvement of Regional Quasi-Geoid in Qomolangma(Mt. Everest) and Determination of Orthometric Elevation[J]. Chinese Journal of Geophysics, 2008, 51(1): 101-107)
(  0) 0) |
| [5] |
郭春喜, 王斌, 程传录, 等. 珠穆朗玛峰高程测量[J]. 地球科学与环境学报, 2009, 31(1): 106-110 (Guo Chunxi, Wang Bin, Cheng Chuanlu, et al. Qomolangma Height Surveying in 2005[J]. Journal of Earth Sciences and Environment, 2009, 31(1): 106-110)
(  0) 0) |
| [6] |
张江齐, 张燕平. 求证珠峰新高[J]. 自然杂志, 2005, 27(5): 283-286 (Zhang Jiangqi, Zhang Yanping. Re-Measurement of New Altitude of Mount Qomolangma[J]. Chinese Journal of Nature, 2005, 27(5): 283-286)
(  0) 0) |
| [7] |
柳建乔. 珠峰测量工作综述[J]. 地理空间信息, 2020, 18(6): 1-5 (Liu Jianqiao. Review about Surveying and Mapping of Mount Qomolangma[J]. Geospatial Information, 2020, 18(6): 1-5)
(  0) 0) |
| [8] |
张赤军. 珠峰高程测定中的有关问题及思考[J]. 武汉大学学报: 信息科学版, 2003, 28(6): 675-678 (Zhang Chijun. Relative Problems and Thoughts on Qomolangma Elevation Determination[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 675-678)
(  0) 0) |
| [9] |
党亚民, 郭春喜, 蒋涛, 等. 2020年珠峰测量与高程确定[J]. 测绘学报, 2021, 50(4): 556-561 (Dang Yamin, Guo Chunxi, Jiang Tao, et al. 2020 Height Measurement and Determination of Mount Qomolangma[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(4): 556-561)
(  0) 0) |
| [10] |
党亚民, 程传录, 杨强, 等. 珠峰及周边地区强震影响垂直形变特征研究[J]. 武汉大学学报: 信息科学版, 2022, 47(1): 26-35 (Dang Yamin, Cheng Chuanlu, Yang Qiang, et al. Vertical Deformation Characteristics Affected by Strong Earthquakes in Mount Qomolangma and Surrounding Areas[J]. Geomatics and Information Science of Wuhan University, 2022, 47(1): 26-35)
(  0) 0) |
| [11] |
王文利, 王斌, 马新莹, 等. 2020年珠峰三角高程测量数据处理与结果分析[J]. 测绘科学, 2022, 47(10): 96-104 (Wang Wenli, Wang Bin, Ma Xinying, et al. 2020 Mount Everest Triangle Elevation Survey Data Processing and Result Analysis[J]. Science of Surveying and Mapping, 2022, 47(10): 96-104)
(  0) 0) |
| [12] |
Förste C, Bruinsma S, Abrykosov O, et al. EIGEN-6C4: The Lasted Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 2190 of GFZ Potsdam and GRGS Toulouse[J]. GFZ Data Service, 2014
(  0) 0) |
| [13] |
Zingerle P, Pail R, Gruber T, et al. The Combined Global Gravity Field Model XGM2019e[J]. Journal of Geodesy, 2020, 94(7): 66 DOI:10.1007/s00190-020-01398-0
(  0) 0) |
| [14] |
蒋涛, 党亚民, 郭春喜, 等. 国际高程参考系统在珠峰地区的实现[J]. 测绘学报, 2022, 51(8): 1 757-1 767 (Jiang Tao, Dang Yamin, Guo Chunxi, et al. Realization of the International Height Reference System in the Region of Mount Qomolangma[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(8): 1 757-1 767)
(  0) 0) |
| [15] |
Sánchez L, Ågren J, Huang J, et al. Basic Agreements for the Computation of Station Potential Values as IHRS Coordinates, Geoid Undulations and Height Anomalies within the Colorado 1 cm Geiod Experiment[R]. Technical University of Munich, Munich, 2018
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100036, China
 2024, Vol. 44
2024, Vol. 44


