2. 中国地震局地震研究所,武汉市洪山侧路40号,430071;
3. 武汉引力与固体潮国家野外观测研究站,武汉市洪山侧路40号,430071
我国是一个地质灾害频发的国家,破坏性的地震往往会造成巨大的人员伤亡和经济损失。预测震后死亡人数对救援工作和物资分配都起着十分关键的作用,而预测地震死亡人数的影响因素错综复杂,传统的方法难以解释地震死亡人数的关键影响因素。张莹等[1]利用层次分析方法构建以地震震级、人口密度、地震烈度、建筑物抗震性能以及发震时刻等主要影响指标形成的指标体系,为后续的震后死亡人数预测提供了重要的参考。
随着机器学习的盛行,许多学者将其应用到地震死亡人数预测中。Tang等[2]采用经验回归法快速估计中国地震伤亡人数;杨帆等[3]和吴昊昱等[4]建立BP神经网络对震后伤亡人数进行快速预测;周德红等[5]将传统的BP神经网络和遗传算法优化的BP神经网络对地震伤亡人数预测模型效果进行对比,结果表明后者精度更高;Li等[6]提出支持向量回归(SVR)的分区伤亡预测方法;王晨晖等[7]和刘立申等[8]分别建立PCA-GSM-SVM和PCA-PSO-SVM模型对地震死亡人数进行预测,并取得良好的效果;Cui等[9]建立集成学习方法分别对地震受伤和死亡人数进行预测。上述研究主要是利用机器学习的不同方法对地震死亡人数进行建模,虽然均有良好的非线性拟合效果,但训练速度慢,网络易陷入局部最优。针对该问题,Huang等[10]提出一种新型的单层前馈神经网络(single-hidden layer feedforward neural network, SLFN),该算法被称为极限学习机(extreme learning machine, ELM)。相比于传统的神经网络,ELM具有学习速度快、精度高、参数设置简单等优势。景国勋等[11]加入预报水平作为影响指标,构建PCA-ELM的地震死亡人数评估模型,并对比ELM和传统的BP神经网络模型,结果表明PCA-ELM模型准确率更高。
基于此,本文对PCA-ELM模型进行改进,引入粒子群优化算法对ELM进行参数优化,构建PCA-PSO-ELM地震死亡人数预测模型。首先对影响指标进行主成分分析降维;然后通过粒子群智能算法对ELM网络权重进行训练优化,避免网络陷入局部最优,得到网络最佳参数;最后对比ELM、PCA-ELM、PCA-PSO-ELM三个模型的预测精度。
1 基本原理和算法流程 1.1 主成分分析(PCA)原理主成分分析本质上是通过线性变换方式将高维数据变换成一组各维度线性无关的数据,其具体计算过程参考文献[12]。主成分分析算法步骤如下:
1) 对数据进行标准化,消除不同量纲和量级的影响。
2) 计算相关系数矩阵。
3) 计算特征值和与之对应的特征向量。通过求解特征方程,计算特征根,按从大到小依次排序,同时得到对应的特征向量。
4) 计算贡献率和累积贡献率。
5) 综合分析。当累积贡献率达到85%~95%时,取前n个主成分作为新的综合指标变量替代原来的高维特征变量。
1.2 粒子群优化算法(PSO)原理在粒子群优化算法模型中,粒子通过群体信息的共享和更新不断优化目标。粒子速度、位置计算公式以及更新公式参考文献[13-14]。
由于惯性权重的大小对算法的搜索能力具有显著影响,其值较大时,有利于全局搜索; 其值较小时,有利于局部搜索。因此,为有效平衡全局搜索与局部搜索能力,使用线性递减权重公式[15]:
| $ \omega(t)=\omega_{\max }-\frac{\left(\omega_{\max }-\omega_{\min }\right)}{T_{\max }} \times t $ | (1) |
式中,ωmax和ωmin分别为惯性权重系数的最大值和最小值,Tmax为粒子群优化算法的最大迭代次数。
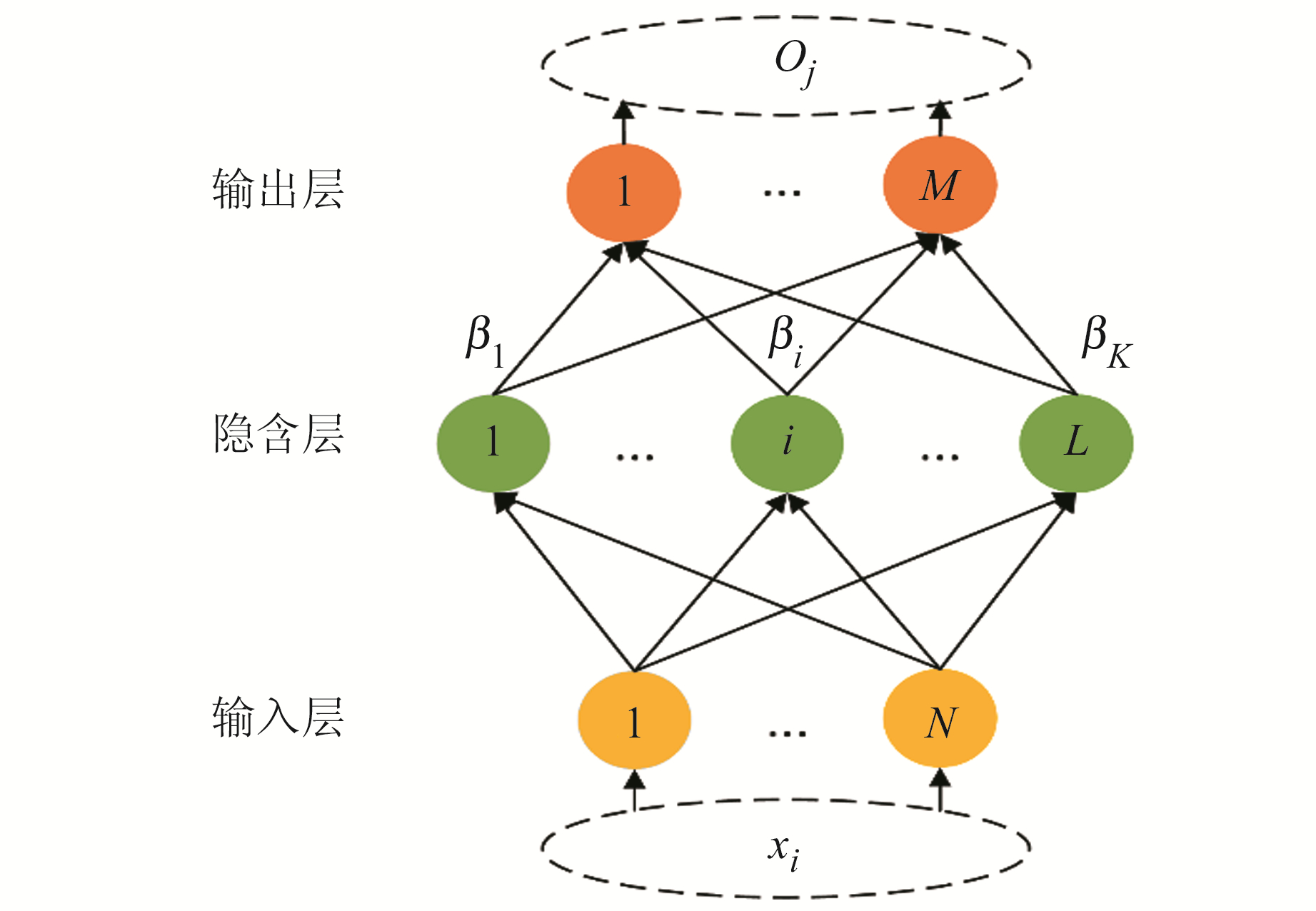
1.3 极限学习机(ELM)原理ELM本质上是一种单隐含层的前馈神经网络,其输入权重和偏置项权重均采用随机生成的方法进行赋值,且其训练方式不采用传统的梯度下降方式,而是在最小二乘法架构下,通过解算对应的广义逆矩阵计算最优输出权值。因此,ELM具有收敛速度快且不易陷入局部最优等优点。ELM网络具体计算过程可参考文献[10],其网络拓扑结构见图 1。
|
图 1 极限学习机网络拓扑结构 Fig. 1 Topological structure of extreme learning machine network |
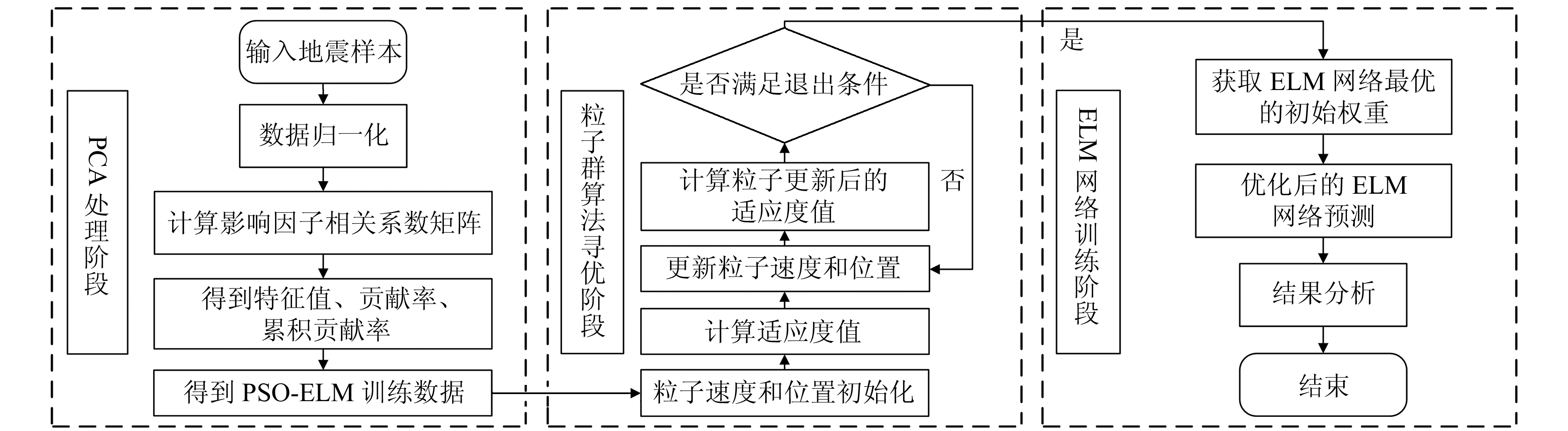
本文提出的PCA-PSO-ELM预测模型流程分为3个阶段:1)PCA处理阶段。通过PCA对影响地震死亡人数的7个影响因子进行降维处理,消除各个影响因子之间的相关性、冗余性。2)粒子群算法寻优阶段。将PCA计算的主成分得分作为PSO-ELM预测模型的输入,设置PSO优化算法的粒子速度、位置等参数和模型终止条件,并进行模型训练。3)ELM网络训练阶段。将PSO优化好的初始权重代入ELM模型进行测试并分析其结果。模型处理流程见图 2。
|
图 2 PCA-PSO-ELM模型流程 Fig. 2 The flow chart of PCA-PSO-ELM model |
影响地震死亡人数的指标错综复杂,本文从数据获取难易程度和重要性角度综合考虑,选取地震震级、震源深度、震中烈度、抗震设防烈度、震中烈度与抗震设防烈度之差(ΔL)、人口密度以及发震时刻等7个影响因素作为模型输入。
地震震级是表示地震强弱的度量,地震震级越大,其对建筑物的破坏力越强,造成的死亡人数也越多。震源深度表示震源在地面上的垂直投影距离,一般来说,震源越靠近地面,对地表的破坏力越强。震中烈度是指地面受到地震震动作用的强烈程度,在同等震级大小条件下,震源深度越浅,震中烈度也越大。抗震设防烈度是在工程建设时对建筑物进行抗震设计的地震烈度,通常情况下,抗震设防水平越高的地区,同等地震条件下造成的人员死亡越少。震中烈度和抗震设防烈度之差(ΔL)可体现建筑物抵御地震破坏的能力,如果ΔL>0且两者差值越大,则说明建筑物抗震能力越弱,地震造成的死亡人数也越多;如果ΔL<0且两者差值的绝对值越小,说明建筑物破坏程度越严重,地震造成的死亡人数也越多。此外,人口密度和发震时间也是直接影响地震死亡人数的重要指标。若地震发生在人口密度大的地区,所造成的人员死亡数远大于人烟稀少地区;若发震时间为夜晚,由于缺少反应时间,死亡人数也会增加。
2.2 数据来源本文从相关文献[5, 7, 11]中筛选42个历史地震震例数据(表 1),选取地震震级、震源深度、震中烈度、抗震设防烈度、震中烈度与抗震设防烈度之差(ΔL)、人口密度以及发震时刻7个影响因子作为网络模型的输入数据,实际死亡人数作为模型的输出数据。
|
|
表 1 地震震例信息 Tab. 1 Information of earthquake cases |
由于抗震设防烈度[16]与发震区域有关,本文选取的是发震地区抗震设防烈度的最大值。发震时刻分为2个时间段:发震时刻“1”表示白天(07:00~19:00),“0”表示夜晚(19:00~次日07:00)。
2.3 主成分分析对原始数据的7个影响因子进行PCA降维处理。表 2为影响因子的特征值、贡献率和累积贡献率,由表可知,前4个主成分累积贡献率达88.607%,说明其包含原始数据的绝大多数信息,满足替代条件。主成分得分是由因子载荷矩阵与原始数据线性组合,计算公式如下:
| $ \left\{\begin{array}{l} Z_1=0.588 S_1+0.167 S_2+0.606 S_3+ \\ \;\;\;\;0.208 S_4+0.438 S_5-0.1 S_6-0.116 S_7 \\ \ Z_2=0.111 S_1+0.345 S_2-0.081 S_3+ \\ \;\;\;\; 0.688 S_4-0.551 S_5+0.079 S_6-0.28 S_7 \\ Z_3=-0.074 S_1+0.587 S_2+0.035 S_3- \\ \;\;\;\;0.146 S_4+0.134 S_5+0.734 S_6+0.267 S_7 \\ Z_4=-0.009 S_1+0.249 S_2+0.032 S_3+ \\ \;\;\;\;0.19 S_4+0.1 S_5-0.447 S_6+0.831 S_7 \end{array}\right. $ | (2) |
|
|
表 2 特征值、贡献率和累积贡献率 Tab. 2 Eigenvalues, contribution rates and cumulative contribution rates |
式中,S1为地震震级,S2为震源深度,S3为震中烈度,S4为抗震设防烈度,S5为震中烈度与抗震设防烈度之差(ΔL),S6为人口密度,S7为发震时刻。将降维后的4个主成分替代原始数据的7个影响因子,并对主成分得分进行归一化处理,公式如下:
| $ X_i^*=\frac{X_i-X_{\min }}{X_{\max }-X_{\min }} $ | (3) |
式中,Xmax、Xmin分别表示每个主成分的最大值、最小值;Xi、Xi*分别表示每个主成分第i个数据和对应的归一化后的数据,最终得到归一化后的主成分得分数据,结果见表 3。
|
|
表 3 主成分得分归一化结果 Tab. 3 Normalized result of principal components |
选取经过PCA处理后的37个震例数据作为训练样本,其余5个数据(样本2、9、15、29、38)作为测试样本。由于地震死亡人数数值离散且跨度较大,为了更直观地对比预测值与真实值,本文采用自然对数对地震死亡人数进行处理。
将4个归一化后的主成分作为输入层节点,取完对数后的地震死亡人数作为输出层节点,构建一个4输入、1输出的3层网络结构,隐含层节点个数采用经验公式[17]
建立好网络模型后,将37个震例数据分别输入到ELM、PCA-ELM和PCA-PSO-ELM模型中进行训练,经过多次实验,得到粒子群优化算法的最佳参数设置和3个模型的训练集预测值与实际值对比结果,具体见表 4和图 3。
|
|
表 4 PSO-ELM网络参数 Tab. 4 PSO-ELM network parameters |
|
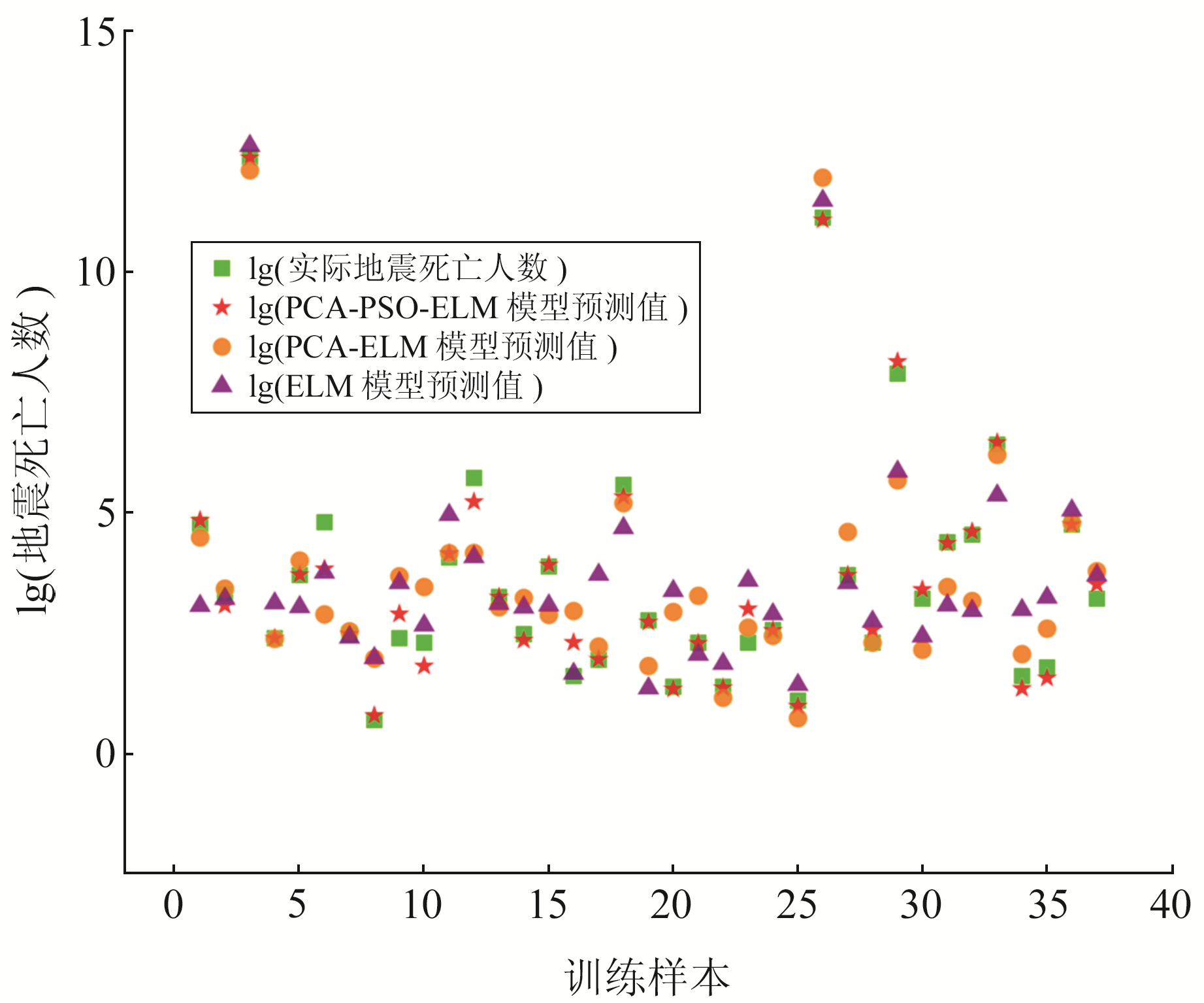
图 3 不同模型训练集预测值与实际值对比 Fig. 3 Comparison between predicted values and actual values of different models |
由图 3可知,除个别样本数据是ELM或PCA-ELM预测值更接近实际值,从整体上看,PCA-PSO-ELM模型的拟合效果最好,其预测值和实际值非常接近,该模型可用于测试样本数据进行预测。
3.2 实验结果及分析选取样本2、9、15、28、36作为测试样本数据检验模型的准确度。将5个测试数据分别代入到ELM、PCA-ELM和PCA-PSO-ELM模型中进行实验,可得到3个模型的预测值和平均误差率结果(表 5)。
|
|
表 5 不同模型结果对比 Tab. 5 Comparison of results of different models |
由表 5可知,未经PCA处理的ELM模型平均误差率为29.25%,而经过PCA处理的ELM模型平均误差率相较前者减少8.70个百分点,说明采用PCA对数据进行预处理十分必要,可以去除原始数据的冗余性。本文提出的PCA-PSO-ELM模型的平均误差率为10.87%,比PCA-ELM模型提高9.68个百分点,说明经过优化的模型可避免网络陷入局部最优,并找到最优的模型参数,进而提高模型的预测精度。因此,该组合模型可为地震死亡人数预测提供新方法。
4 结语本文利用主成分分析对原始数据特征进行降维,再通过粒子群优化极限学习机网络对数据进行仿真实验,对比3个模型的实验结果,得到以下结论:
1) 在众多影响地震死亡人数的因素中,构建以地震震级、震源深度、震中烈度、抗震设防烈度、震中烈度与抗震设防烈度之差(ΔL)、人口密度以及发震时刻为主的影响指标体系。
2) 经过PCA降维处理,能够极大地去除原始数据之间的相关性和冗余性,可强化模型的泛化性,提升模型的预测精度。
3) 对比ELM模型和PCA-ELM模型,本文提出的PCA-PSO-ELM模型不仅能避免网络陷入局部最优,而且模型的预测值与实际值的平均误差率最低,可为地震死亡人数预测提供一种新的评估方法。
然而,由于收集的历史震例数据还不够丰富,构建影响地震死亡人数的评估体系还不够完善,此外模型精度和稳定性仍有进一步提高的空间,这将是未来研究的重点。
| [1] |
张莹, 尹文刚, 郭红梅, 等. 地震灾害人员伤亡关键影响因素指标体系构建[J]. 防灾减灾学报, 2017, 33(4): 87-94 (Zhang Ying, Yin Wengang, Guo Hongmei, et al. The Construction of Earthquake Disaster Casualties Key Influence Factors Index System[J]. Journal of Disaster Prevention and Reduction, 2017, 33(4): 87-94)
(  0) 0) |
| [2] |
Tang B H, Chen Q, Liu X, et al. Rapid Estimation of Earthquake Fatalities in China Using an Empirical Regression Method[J]. International Journal of Disaster Risk Reduction, 2019, 41
(  0) 0) |
| [3] |
杨帆, 郑宝柱, 剡亮亮. 基于BP神经网络的地震伤亡人数评估体系研究[J]. 震灾防御技术, 2009, 4(4): 428-435 (Yang Fan, Zheng Baozhu, Yan Liangliang. System of Earthquake Casualty Assessment Based on BP Neural Network[J]. Technology for Earthquake Disaster Prevention, 2009, 4(4): 428-435 DOI:10.3969/j.issn.1673-5722.2009.04.008)
(  0) 0) |
| [4] |
吴昊昱, 吴新燕, 李宏伟. 基于神经网络的地震死亡人数快速评估研究[J]. 科技通报, 2017, 33(4): 241-244 (Wu Haoyu, Wu Xinyan, Li Hongwei. Research on Rapid Assessment of Earthquake Death Toll Based on Neural Network[J]. Bulletin of Science and Technology, 2017, 33(4): 241-244)
(  0) 0) |
| [5] |
周德红, 冯豪, 程乐棋, 等. 遗传算法优化的BP神经网络在地震死亡人数评估中的应用[J]. 安全与环境学报, 2017, 17(6): 2 267-2 272 (Zhou Dehong, Feng Hao, Cheng Leqi, et al. Earthquake Casualty Assessment Based on the BP Neural Network of the Optimized Genetic Algorithm[J]. Journal of Safety and Environment, 2017, 17(6): 2 267-2 272 DOI:10.13637/j.issn.1009-6094.2017.06.043)
(  0) 0) |
| [6] |
Li B Y, Gong A D, Zeng T T, et al. A Zoning Earthquake Casualty Prediction Model Based on Machine Learning[J]. Remote Sensing, 2021, 14(1)
(  0) 0) |
| [7] |
王晨晖, 袁颖, 刘立申, 等. 基于PCA-GSM-SVM的地震伤亡人数预测[J]. 华北地震科学, 2019, 37(3): 25-30 (Wang Chenhui, Yuan Ying, Liu Lishen, et al. Earthquake Casualties Prediction Based on PCA-GSM-SVM[J]. North China Earthquake Sciences, 2019, 37(3): 25-30)
(  0) 0) |
| [8] |
刘立申, 王晨晖, 王利兵, 等. 基于PCA-PSO-SVM的地震死亡人数预测模型研究[J]. 地震地磁观测与研究, 2019, 40(5): 41-47 (Liu Lishen, Wang Chenhui, Wang Libing, et al. Earthquake Casualties Prediction Model Based on PCA-PSO-SVM[J]. Seismological and Geomagnetic Observation and Research, 2019, 40(5): 41-47)
(  0) 0) |
| [9] |
Cui S Z, Yin Y Q, Wang D J, et al. A Stacking-Based Ensemble Learning Method for Earthquake Casualty Prediction[J]. Applied Soft Computing, 2021, 101
(  0) 0) |
| [10] |
Huang G B, Zhu Q Y, Siew C K. Extreme Learning Machine: A New Learning Scheme of Feedforward Neural Networks[C]. 2004 IEEE International Joint Conference on Neural Networks, Budapest, 2004
(  0) 0) |
| [11] |
景国勋, 邢丽华, 邓奇根. 基于PCA-ELM的地震死亡人数评估[J]. 安全与环境学报, 2020, 20(2): 617-623 (Jing Guoxun, Xing Lihua, Deng Qigen. Evaluation of the Earthquake Death Toll Based on the PCA-ELM Analysis[J]. Journal of Safety and Environment, 2020, 20(2): 617-623)
(  0) 0) |
| [12] |
王炜, 林命週, 马钦忠, 等. 主成分分析法在地震预测中的应用研究[J]. 中国地震, 2005, 21(3): 409-416 (Wang Wei, Lin Mingzhou, Ma Qinzhong, et al. The Primary Component Analysis Method and Its Application in Earthquake Prediction[J]. Earthquake Research in China, 2005, 21(3): 409-416)
(  0) 0) |
| [13] |
Kennedy J, Eberhart R. Particle Swarm Optimization[C]. ICNN'95-International Conference on Neural Networks, Perth, 2002
(  0) 0) |
| [14] |
Eberhart R, Kennedy J. A New Optimizer Using Particle Swarm Theory[C]. The Sixth International Symposium on Micro Machine and Human Science, Nagoya, 2002
(  0) 0) |
| [15] |
韩亚鹏, 弓旭峰, 高有山, 等. 利用PSO-GA算法的桥式起重机结构轻量化设计[J]. 起重运输机械, 2020(20): 125-131 (Han Yapeng, Gong Xufeng, Gao Youshan, et al. Lightweight Design of Bridge Crane Structure Based on PSO-GA Algorithm[J]. Hoisting and Conveying Machinery, 2020(20): 125-131)
(  0) 0) |
| [16] |
中华人民共和国住房和城乡建设部. GB50011-2010建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010 (Ministry of Housing and Urban-Rural Construction of the People's Republic of China. GB50011-2010 Code for Seismic Design of Buildings[S]. Beijing: China Architecture and Building Press, 2010)
(  0) 0) |
| [17] |
沈花玉, 王兆霞, 高成耀, 等. BP神经网络隐含层单元数的确定[J]. 天津理工大学学报, 2008, 24(5): 13-15 (Shen Huayu, Wang Zhaoxia, Gao Chengyao, et al. Determining the Number of BP Neural Network Hidden Layer Units[J]. Journal of Tianjin University of Technology, 2008, 24(5): 13-15)
(  0) 0) |
2. Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China;
3. Wuhan Gravitation and Solid Earth Tides, National Observation and Research Station, 40 Hongshance Road, Wuhan 430071, China
 2024, Vol. 44
2024, Vol. 44

