工业机器人具有可靠性高、重复精度高、适用性强等特点,作为制造业发展的“催化剂”,其在军事、医疗、数控加工等领域应用广泛[1]。通常,工业机器人重复精度较高,但绝对精度较低[2],制约了其在精密加工、航天装配等先进制造领域的应用。实际使用中,可通过标定来提高工业机器人的绝对定位精度,获取激光跟踪仪与机器人基坐标系的转换关系是进行标定的基础,进而将不同的坐标测量数据统一到相同坐标系下。目前,常用的机器人末端位姿测量设备有视觉测量系统、球杆仪、激光跟踪仪等[3-4],其中激光跟踪仪最为常用。
文献[5]采用基于平面拟合的转换方法,利用机器人自身的结构关系求解转换关系,但因机器人基座安装平面较大,受制于加工安装精度,安装平面与机器人基坐标系平面不完全重合;文献[6]需要控制机器人作3次单轴旋转,而后根据空间几何关系和位置关系反推转换关系;文献[7]通过控制机器人沿机器人基坐标系运动,拟合得到方向向量,而后再进一步求解平移参数。
上述方法现场操作复杂,容易受到场地和安装因素的影响,拟合精度不高,且需要采集足够多的点去提高拟合精度,效率较低。为此,本文提出一种工具坐标系标定与公共点转换相结合的坐标转换方法,只需控制机器人采集较少的点,具有操作简单、使用范围广等优点,适合工业现场使用。
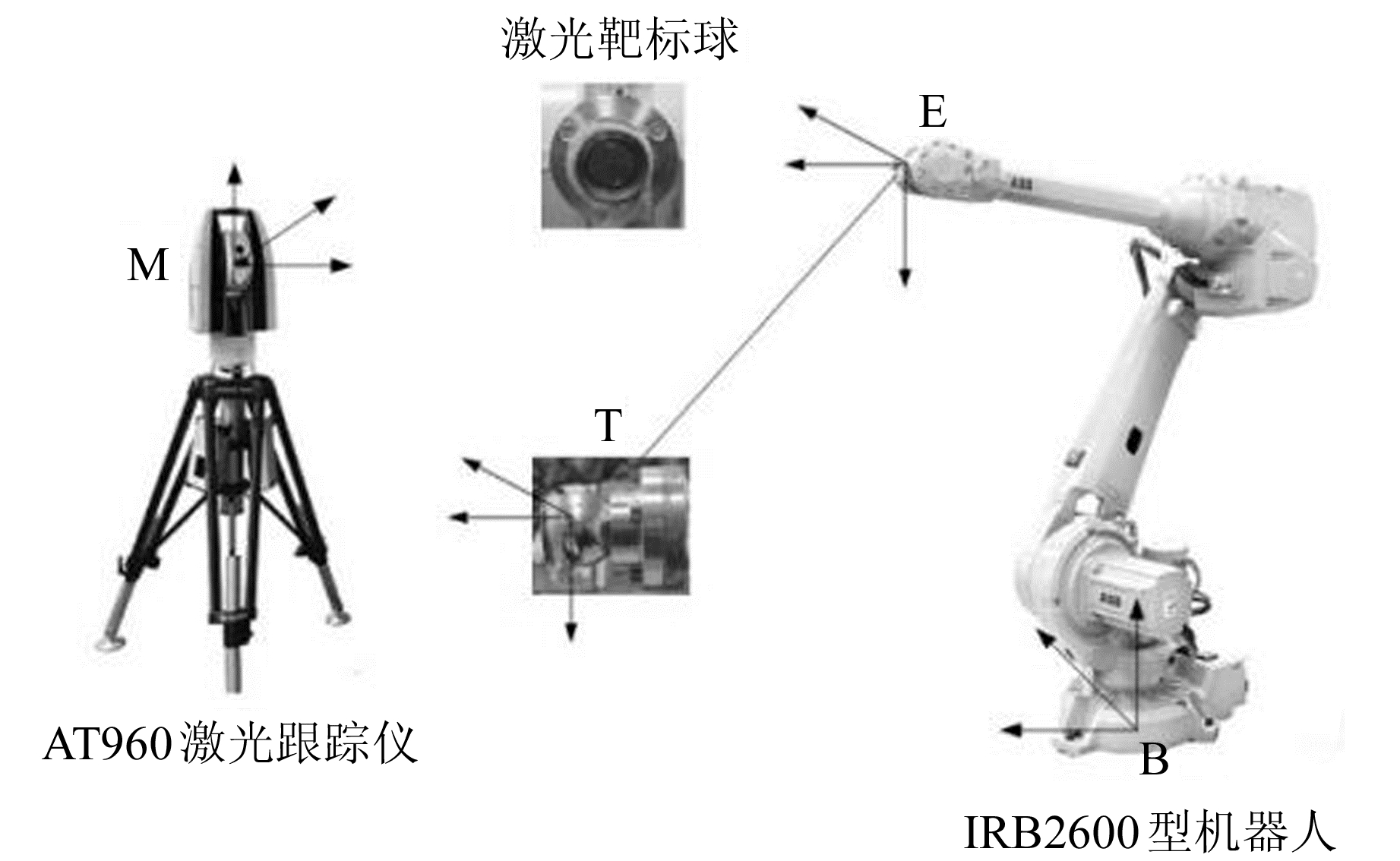
1 坐标系转换方法坐标系转换系统包含工业机器人、激光跟踪仪、靶标球和控制系统,如图 1所示,在机器人末端固定靶标基座放置激光靶球。其中,{B}为机器人基坐标系,位于机器人安装底座平面,它是其他坐标系的参考基准;{E}为法兰末端坐标系,固连在机器人连杆末端;{M}为激光跟踪仪坐标系;{T}为工具坐标系,固定在机器人末端夹具上,用来描述工具中心点的位置和工具姿态。
|
图 1 坐标系转换实验系统示意图 Fig. 1 Experimental system for coordinate transformation |
坐标系之间的转换关系可以用齐次变换矩阵来表示,机器人法兰末端坐标系{E}到机器人基坐标系{B}的位姿变换关系用EBT来表示。同理,工具坐标系{T}到机器人基坐标系{B}的位姿变换用TBT表示,工具坐标系{T}到法兰末端坐标系{E}的位姿变换用TET表示。位姿变换矩阵为:
| $\begin{gathered} { }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}=\left[\begin{array}{cc} {}_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{R} & { }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{P} \\ 0 & 1 \end{array}\right], { }_{\mathrm{T}}^{\mathrm{B}} \boldsymbol{T}=\left[\begin{array}{cc} { }_{\mathrm{T}}^{\mathrm{B}} \boldsymbol{R} & { }_{\mathrm{T}}^{\mathrm{B}} \boldsymbol{P} \\ 0 & 1 \end{array}\right], \\ { }_{\mathrm{T}}^{\mathrm{E}} \boldsymbol{T}=\left[\begin{array}{cc} { }_{\mathrm{T}}^{\mathrm{E}} \boldsymbol{R} & { }_{\mathrm{T}}^{\mathrm{E}} \boldsymbol{P} \\ 0 & 1 \end{array}\right] \end{gathered}$ | (1) |
式中,R为两个坐标系之间的旋转变换矩阵,P为两个坐标系之间的平移变换矩阵。
上述坐标系转换关系满足:
| ${ }_{\mathrm{T}}^{\mathrm{B}} \boldsymbol{T}={ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}_{\mathrm{T}}^{\mathrm{E}} \boldsymbol{T}$ | (2) |
结合位姿变换矩阵可表示为:
| $\left[\begin{array}{cc} { }_{\mathrm{T}}^{\mathrm{B}} \boldsymbol{R} & { }_{\mathrm{T}}^{\mathrm{B}} \boldsymbol{P} \\ 0 & 1 \end{array}\right]=\left[\begin{array}{cc} { }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{R} & { }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{P} \\ 0 & 1 \end{array}\right]\left[\begin{array}{cc} { }_{\mathrm{T}}^{\mathrm{E}} \boldsymbol{R} & { }_{\mathrm{T}}^{\mathrm{E}} \boldsymbol{P} \\ 0 & 1 \end{array}\right]$ | (3) |
由式(2)可得:
| ${ }_{\mathrm{T}}^{\mathrm{B}} \boldsymbol{R}={ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{R}_{\mathrm{T}}^{\mathrm{E}} \boldsymbol{R} $ | (4) |
| ${ }_{\mathrm{T}}^{\mathrm{B}} \boldsymbol{P}={ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{R}_{\mathrm{T}}^{\mathrm{E}} \boldsymbol{P}+{ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{P}$ | (5) |
工具坐标系固定在连杆末端,其相对于法兰末端坐标系的位姿变换关系TET是不变的,工具坐标系的标定实质就是确定矩阵TET中的参数值。本文中,O点表示光学靶标球中心点(tool center point,TCP),标定TCP在法兰末端坐标系的位置后,通过式(5)可求得其在机器人基坐标系{B}中的位置。O点相对于跟踪仪坐标系{M}的位置坐标可以通过激光跟踪仪测得,根据公共点转换即可求得机器人坐标系与激光跟踪仪坐标系的转换关系。算法流程如图 2所示。

|
图 2 坐标系转换算法流程 Fig. 2 Flow chart of coordinate system transformation algorithm |
光学TCP位置O点在机器人基坐标系{B}中可表示为:
| ${ }_{\mathrm{T}}^{\mathrm{B}} \boldsymbol{P}(i)={ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}(i){ }_{\mathrm{T}}^{\mathrm{E}} \boldsymbol{P}$ | (6) |
式中,i为TCP在空间中的位置点号,EBT为机器人法兰末端坐标系{E}到机器人基坐标系{B}的位姿变换矩阵,TEP为TCP在法兰末端坐标系中的位置。在空间中不同的测量位置点(m,n),TCP在机器人基坐标系下的坐标差为:
| $\begin{aligned} \Delta \boldsymbol{P}_{\mathrm{B}}^{m m} & ={ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}(m){ }_{\mathrm{E}}^{\mathrm{T}} \boldsymbol{P}-{ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}(n)_{\mathrm{E}}^{\mathrm{T}} \boldsymbol{P}= \\ & \left({ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}(m)-{ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}(n)\right)_{\mathrm{E}}^{\mathrm{T}} \boldsymbol{P} \end{aligned}$ | (7) |
在激光跟踪仪坐标系下的坐标差为:
| $\Delta \boldsymbol{P}_M^{m m}=\boldsymbol{P}_T^M(m)-\boldsymbol{P}_T^M(n)$ | (8) |
空间中任意两点在不同坐标系下的距离相等(假设坐标系之间尺度因子为1),对于光学TCP在空间中的任意两点,尽管其在跟踪仪坐标系和机器人基坐标系的坐标值不同,但这两个点之间的距离相等,即
| $\left\|\Delta \boldsymbol{P}_B^{n m}\right\|_2=\left\|\Delta \boldsymbol{P}_M^{m n}\right\|_2$ | (9) |
从而可以得到:
| $\begin{gathered} \left\|\left({ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}(m)-{ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}(n)\right)_{\mathrm{E}}^{\mathrm{T}} \boldsymbol{P}\right\|_2= \\ \left\|\boldsymbol{P}_T^{\mathrm{M}}(m)-\boldsymbol{P}_T^M(n)\right\|_2 \end{gathered}$ | (10) |
令
| $\begin{gathered} { }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}(m)-{ }_{\mathrm{E}}^{\mathrm{B}} \boldsymbol{T}(n)=\left[\begin{array}{cccc} t_{11}^{m n} & t_{12}^{m n} & t_{13}^{m n} & t_{14}^{m n} \\ t_{21}^{m n} & t_{22}^{m n} & t_{23}^{m n} & t_{24}^{m n} \\ t_{31}^{m n} & t_{32}^{m n} & t_{33}^{m n} & t_{34}^{m n} \\ 0 & 0 & 0 & 0 \end{array}\right], \\ { }_{\mathrm{E}}^{\mathrm{T}} \boldsymbol{P}=\left[\begin{array}{c} t_x \\ t_y \\ t_z \\ 1 \end{array}\right], \boldsymbol{P}_T^M(m)-\boldsymbol{P}_T^M(n)=\left[\begin{array}{c} p M_0 \\ p M_1 \\ p M_2 \\ 1 \end{array}\right] \end{gathered}$ | (11) |
式中,tijmn为在机器人基坐标系下两点末端位姿对应位置元素的差值,ETP为光学TCP相对于末端法兰坐标系的平移变换矩阵。
可以得到:
| $\left\|\left[\begin{array}{cccc} t_{11}^{m n} & t_{12}^{m n} & t_{13}^{m m} & t_{14}^{m n} \\ t_{21}^{m n} & t_{22}^{m n} & t_{23}^{m m} & t_{24}^{m n} \\ t_{31}^{m n} & t_{32}^{m m} & t_{33}^{m n} & t_{34}^{m n} \\ 0 & 0 & 0 & 0 \end{array}\right]\left[\begin{array}{c} t_x \\ t_y \\ t_z \\ 1 \end{array}\right]\right\|=\left\|\left[\begin{array}{c} p M_0 \\ p M_1 \\ p M_2 \\ 1 \end{array}\right]\right\|$ | (12) |
展开可得:
| $\begin{gathered} \sum\limits_{j=1}^3\left(t_{j 1}^{m m} x+t_{j 2}^{m n} y+t_{j 3}^{m n} z+t_{j 4}^{m n}\right)^2- \\ \left(p M_0^2+p M_1^2+p M_2^2\right)=0 \end{gathered}$ | (13) |
公式(8)是非线性方程,对其进行线性化,一阶泰勒展开后,忽略高阶项整理得到:
| $\begin{gathered} 2 \sum\limits_{j=1}^3\left(t_{j 1}^{m n} x_0+t_{j 2}^{m n} y_0+t_{j 3}^{m n} z_0+t_{j 4}^{m n}\right) \cdot \\ \quad\left(t_{j 1}^{m n} x+t_{j 2}^{m n} y+t_{j 3}^{m n} z\right)+l=0 \end{gathered}$ | (14) |
式中,
| $\begin{gathered} l=\sum\limits_{j=1}^3\left(t_{j 1}^{m n} x_0+t_{j 2}^{m n} y_0+t_{j 3}^{m n} z_0+t_{j 4}^{m n}\right)^2- \\ \left(p M_0^2+p M_1^2+p M_2^2\right)- \\ 2 \sum\limits_{j=1}^3\left(t_{j 1}^{m n} x_0+t_{j 2}^{m n} y_0+t_{j 3}^{m n} z_0+t_{j 4}^{m n}\right) \cdot \\ \left(t_{j 1}^{m n} x_0+t_{j 2}^{m n} y_0+t_{j 3}^{m n} z_0\right) \end{gathered}$ | (15) |
整理化简可得:
| $\left[\begin{array}{lll} a_{i 1} & a_{i 2} & a_{i 3} \end{array}\right]\left[\begin{array}{l} t_x \\ t_y \\ t_z \end{array}\right]=-l$ | (16) |
式中,
| $\begin{aligned} & a_{i 1}=2 \sum\limits_{j=1}^3 t_{j 1}^{m n}\left(t_{j 1}^{m n} x_0+t_{j 2}^{m n} y_0+t_{j 3}^{m n} z_0+t_{j 4}^{m n}\right) \\ & a_{i 2}=2 \sum\limits_{j=1}^3 t_{j 2}^{m n}\left(t_{j 1}^{m n} x_0+t_{j 2}^{m n} y_0+t_{j 3}^{m n} z_0+t_{j 4}^{m n}\right) \\ & a_{i 3}=2 \sum\limits_{j=1}^3 t_{j 3}^{m n}\left(t_{j 1}^{m n} x_0+t_{j 2}^{m n} y_0+t_{j 3}^{m n} z_0+t_{j 4}^{m n}\right) \end{aligned}$ | (17) |
观察方程参数个数可知,至少需要机器人运动到3个位置(不共线),才能使得方程有唯一解。通常为了减少实验过程中随机误差的影响,采集的观测点数远大于3。根据建立的方程组,通过最小二乘法即可得到TCP在法兰末端坐标系下的位置,完成光学TCP位置标定。
1.2 重心化配置进行坐标系转换,需要在不同的测量坐标系下观测同一组公共点。在不同的坐标系下,可将公共观测点组合起来等效为刚体,坐标系之间的变换关系可等效为刚体之间的位姿变换。
由刚体运动理论可知,在进行刚体变换时,其内部各点的相对位置保持不变,即两个刚体上的各公共点到质心的距离保持不变。本文将公共观测点组合等效为刚体,根据重心不变理论,对机器人基坐标系和激光跟踪仪坐标系下的公共观测点进行重心化配置,各公共点到重心的距离不变,相同点对应距离相等:
| $\boldsymbol{P}_g^{\mathrm{B}}=\left[\begin{array}{c} x_{\mathrm{B}g}=\frac{\sum\limits_{i=1}^n x_i}{n} \\ y_{\mathrm{B}g}=\frac{\sum\limits_{i=1}^n y_i}{n} \\ z_{\mathrm{B}g}=\frac{\sum\limits_{i=1}^n z_i}{n} \end{array}\right], \boldsymbol{P}_g^{\mathrm{M}}=\left[\begin{array}{c} X_{\mathrm{M}g}=\frac{\sum\limits_{i=1}^n X_i}{n} \\ Y_{\mathrm{M}g}=\frac{\sum\limits_{i=1}^n Y_i}{n} \\ Z_{\mathrm{M}g}=\frac{\sum\limits_{i=1}^n Z_i}{n} \end{array}\right]$ | (18) |
式中,PgB和PgM分别为采样点在机器人基坐标系和激光跟踪仪坐标系下的等效刚体重心,(xi, yi, zi)为观测点在机器人基坐标系下的坐标值,(Xi, Yi, Zi)为观测点在激光跟踪仪坐标系下的坐标值,n为公共点的个数。
对各观测点进行等效刚体的空间重心化配置,可得:
| $\boldsymbol{P}_{g_i}^{\mathrm{B}}=\boldsymbol{P}_i^{\mathrm{B}}-\boldsymbol{P}_g^{\mathrm{B}}=\left[\begin{array}{c} x_i-x_{\mathrm{B}g} \\ y_i-y_{\mathrm{B}g} \\ z_i-z_{\mathrm{B}g} \end{array}\right]=\left[\begin{array}{c} x_{g_i} \\ y_{g_i} \\ z_{g_i} \end{array}\right]$ | (19) |
| $\boldsymbol{P}_{g_i}^{\mathrm{M}}=\boldsymbol{P}_i^{\mathrm{M}}-\boldsymbol{P}_g^{\mathrm{M}}=\left[\begin{array}{c} X_i-X_{\mathrm{M}g} \\ Y_i-Y_{\mathrm{M}g} \\ Z_i-Z_{\mathrm{M}g} \end{array}\right]=\left[\begin{array}{c} X_{g_i} \\ Y_{g_i} \\ Z_{g_i} \end{array}\right]$ | (20) |
式中,PgiB和PgiM分别为第i个公共点在机器人基坐标系和激光跟踪仪坐标系下的等效重心化位置点坐标。
重心化空间配置消去了坐标系变换的平移变换,减小了参与计算的坐标数值,能在一定程度上降低机器人绝对定位误差和测量误差造成的影响,增强数值计算的可靠性。
1.3 坐标系转换坐标系转换模型用来描述两个坐标系之间的转换关系,包含四参数、七参数等转换模型[8-11]。本文采用三维七参数转换模型,不考虑尺度因子。重心化配置坐标后消去了平移参数,姿态变换矩阵即为机器人基坐标系到跟踪仪坐标系的旋转矩阵。假设光学TCP位置点O在机器人基坐标系{B}中的等效重心化坐标为(xgi, ygi, zgi),在激光跟踪仪坐标系{M}中等效重心化的坐标为(Xgi, Ygi, Zgi),两个坐标系之间的转换关系为:
| $\left[\begin{array}{l} X_{g_i} \\ Y_{g_i} \\ Z_{g_i} \end{array}\right]=\boldsymbol{R}\left[\begin{array}{l} x_{g_i} \\ y_{g_i} \\ z_{g_i} \end{array}\right]$ | (21) |
式中,R为机器人基坐标系{B}到跟踪仪坐标系{M}的齐次变换旋转矩阵:
| $\boldsymbol{R}=R(\gamma) R(\beta) R(\alpha)$ | (22) |
式中,(γ, β, α)为旋转参数。
选取3个以上的公共点代入式(21)可构成超定方程组,采用迭代最小二乘法求解,可以得到机器人基坐标系到跟踪仪坐标系的旋转矩阵 R。而后通过式(23)可求得机器人基坐标系相对于跟踪仪坐标系的齐次变换平移矩阵 T:
| $\boldsymbol{T}=\left[\begin{array}{c} T_x \\ T_y \\ T_z \end{array}\right]=\frac{1}{n} \sum\limits_{i=1}^n\left(\left[\begin{array}{l} X_{g_i} \\ Y_{g_i} \\ Z_{g_i} \end{array}\right]-\boldsymbol{R}\left[\begin{array}{c} x_{g_i} \\ y_{g_i} \\ z_{g_i} \end{array}\right]\right)$ | (23) |
考虑到测量误差和机器人定位误差的存在,O点从机器人基坐标系{B}经坐标转换后在激光跟踪仪坐标系{M}中的坐标(X′, Y′, Z′)与其目标点坐标(X0, Y0, Z0)存在差异,转换后的坐标残差为:
| $\left\{\begin{array}{l} v_X=X_0-X^{\prime} \\ v_Y=Y_0-Y^{\prime} \\ v_Z=Z_0-Z^{\prime} \end{array}\right.$ | (24) |
本文实验系统由ABB IRB2600型工业机器人、激光跟踪仪、光学靶标球和控制系统组成。将光学靶标球的工件固定于机器人末端法兰盘上,实验过程中确保机器人和激光跟踪仪相对位置不变。实验中用到的激光跟踪仪型号为Lecia AT960,测量精度为±(15 μm+6 μm/m),配合使用的靶标球为直径38.1 mm的RRR1.5″精密靶球,在10 m的工作范围内点位精度优于75 μm。IRB2600型工业机器人重复定位精度为0.1 mm,绝对定位精度为1 mm左右。为了验证本文方法的有效性,与文献[6]的方法进行对比。实验时按照文献[6]所述方法控制机器人作单轴旋转运动,按照一定的角度值停止单轴运动并记录激光跟踪仪点位读数。
2.1 光学TCP位置标定实验首先对光学TCP位置进行标定。将机器人运动到初始零位,在机器人工作空间中,随机选取25个点位,各位置点尽可能分布均匀,控制机器人分别运动到这25个位置。用激光跟踪仪观测25个点位的坐标,同时记录下机器人运动到相应点位时的法兰末端位姿。
根据文献[3]可知,尽管求解线性方程最低只需要3组数据,但由于机器人存在定位误差,会对非线性方程组系数矩阵产生较大影响,导致求解结果不稳定。为提高求解精度,本文从采集的点集中选取10组数据点进行光学TCP位置标定。表 1为观测点在激光跟踪仪测量坐标系下的位置坐标。
|
|
表 1 观测点在激光跟踪仪中的测量坐标 Tab. 1 Measurement coordinates of observation points in laser tracker |
选取的10个观测点相应地在机器人坐标系中测得的法兰末端位姿如表 2所示,其中(X, Y, Z)表示法兰末端坐标系相对于机器人基坐标系的平移量,(Q1, Q2, Q3, Q4)表示法兰末端坐标系相对于机器人基坐标系的旋转变换四元数。根据实验数据,采用上文所述的距离约束法原理计算求得光学TCP在法兰末端坐标系下的位置为(0.357 2, 0.278 9, 39.430 6)T,进一步可以计算得到这10个观测点在机器人基坐标系的位置坐标(表 3)。
|
|
表 2 观测点末端法兰位姿 Tab. 2 Pose of the end Flange of the observation point |
|
|
表 3 观测点在机器人基坐标系中的坐标 Tab. 3 Coordinates of the observation points in the robot base system |
根据文献[6]方法,采集数据点进行拟合,通过计算得到的机器人基坐标系相对于激光跟踪仪坐标系的齐次变换矩阵为:
| $ { }_{\mathrm{B}}^{\mathrm{M}} \boldsymbol{T}_1=\left[\begin{array}{rrrr} -0.723000 & 0.690826 & -0.005570 & 3517.036 \\ -0.690820 & -0.723020 & -0.003700 & 2551.458 \\ -0.006580 & 0.001171 & 0.999978 & -1454.8310 \end{array}\right] $ |
根据已经标定光学TCP位置的10个点,采用本文方法进行公共点转换求解,10个观测点在机器人基坐标系的坐标值如表 3所示。经计算,求解得到的机器人基坐标系相对于激光跟踪仪坐标系的齐次变换矩阵为:
| $ { }_{\mathrm{B}}^{\mathrm{M}} \boldsymbol{T}_2=\left[\begin{array}{cccc} -0.723000 & 0.690826 & -0.005697 & 3517.201 \\ -0.690820 & -0.723020 & -0.003701 & 2551.910 \\ -0.006580 & 0.001170 & 0.999977 & -1453.650 \\ 0 & 0 & 0 & 1 \end{array}\right] $ |
为对比两种方法的转换精度,在前期采集的点集中随机选取10个点,根据标定的光学TCP位置计算靶球在机器人基坐标系中的位置,如表 4所示。分别通过本文方法和文献[9]方法求解得到坐标转换齐次矩阵,将10个测试点在机器人基坐标系下的位置坐标转换到激光跟踪仪坐标系下,与相应点的激光跟踪仪实测坐标数值进行对比,两种方法的坐标转换较差如表 5和表 6所示。
|
|
表 4 测试点在机器人基坐标系中的坐标 Tab. 4 Coordinates of test points in the robot base system |
|
|
表 5 测试点在文献[9]算法下的坐标转换数据 Tab. 5 The coordinate conversion data of the test points under the algorithm in literature [9] |
|
|
表 6 测试点在本文算法下的转换数据 Tab. 6 The coordinate conversion data of the test points under the algorithm in this paper |
本文采用MAE作为精度评价指标,其具体计算如下:
| $\text { MAE }=\frac{1}{n} \sum\limits_{i=1}^n\left|O_{\text {test }}^{(i)}-O_{\text {test }}^{\prime(i)}\right|$ | (25) |
式中,Otest(i)表示第i个测试点TCP在跟踪仪坐标系中的测量值,O′test(i)表示该点TCP在机器人基坐标系下的坐标转换到跟踪仪坐标系下的值,n表示测试点的个数。
统计两种方法3个坐标轴分量的转换精度MAE和点位综合转换精度MAE(表 7)可知,相比于传统的拟合法,采用本文方法进行坐标转换后,在X轴、Y轴、Z轴方向的MAE分别减小18.83%、36.86%和44.87%,综合MAE减小35.44%。坐标转换结果的较差受采样点坐标测量的影响,文献[9]算法需要控制机器人作多次单轴旋转运动,拟合精度取决于每个停顿位置采集靶标球球心的测量坐标值,机器人定位误差会造成圆的拟合精度损失,最终影响坐标系转换的精度。相对而言,本文算法可有效避免拟合误差的影响,测试点经转换后的转换误差有所减小,转换精度较文献[9]算法一定程度的提高,证明了本文方法的有效性。
|
|
表 7 测试点坐标转换精度整体统计 Tab. 7 Test point coordinate conversion accuracy |
本文提出一种工具坐标系标定与公共点转换相结合的求解机器人基坐标系与激光跟踪仪坐标系转换关系的新方法,与传统基于拟合的坐标转换方法相比,本文方法能有效避免传统方法的拟合误差,减小因测量误差和定位误差对坐标转换关系的影响,提高坐标转换精度。且该方法操作简单,只需要移动机器人采集少量的点,不需要作单轴旋转运动或者沿机器人基坐标系轴线作直线运动,简化了操作流程,测量效率高,适合工业现场使用。
| [1] |
冯旭, 宋明星, 倪笑宇, 等. 工业机器人发展综述[J]. 科技创新与应用, 2019(24): 52-54 (Feng Xu, Song Mingxing, Ni Xiaoyu, et al. Overview of Industrial Robot Development[J]. Technology Innovation and Application, 2019(24): 52-54)
(  0) 0) |
| [2] |
温秀兰, 芮平, 张颖, 等. 工业机器人几何参数标定综述[J]. 南京工程学院学报: 自然科学版, 2017, 15(4): 1-7 (Wen Xiulan, Rui Ping, Zhang Ying, et al. Survey on Industry Robot Geometry Parameters Calibration[J]. Journal of Nanjing Institute of Technology: Natural Science Edition, 2017, 15(4): 1-7)
(  0) 0) |
| [3] |
周炜, 廖文和, 田威. 基于空间插值的工业机器人精度补偿方法理论与试验[J]. 机械工程学报, 2013, 49(3): 42-48 (Zhou Wei, Liao Wenhe, Tian Wei. Theory and Experiment of Industrial Robot Accuracy Compensation Method Based on Spatial Interpolation[J]. Journal of Mechanical Engineering, 2013, 49(3): 42-48)
(  0) 0) |
| [4] |
刘常杰, 段宇, 王一, 等. 机器人柔性坐标测量系统现场校准技术研究[J]. 机械工程学报, 2010, 46(18): 1-6 (Liu Changjie, Duan Yu, Wang Yi, et al. Study on the Field Calibration Technology of Robot Flexible Coordinate Measurement System[J]. Journal of Mechanical Engineering, 2010, 46(18): 1-6)
(  0) 0) |
| [5] |
任永杰, 邾继贵, 杨学友, 等. 利用激光跟踪仪对机器人进行标定的方法[J]. 机械工程学报, 2007, 43(9): 195-200 (Ren Yongjie, Zhu Jigui, Yang Xueyou, et al. Method of Robot Calibration Based on Laser Tracker[J]. Chinese Journal of Mechanical Engineering, 2007, 43(9): 195-200)
(  0) 0) |
| [6] |
张博, 魏振忠, 张广军. 机器人坐标系与激光跟踪仪坐标系的快速转换方法[J]. 仪器仪表学报, 2010, 31(9): 1 986-1 990 (Zhang Bo, Wei Zhenzhong, Zhang Guangjun. Rapid Coordinate Transformation between a Robot and a Laser Tracker[J]. Chinese Journal of Scientific Instrument, 2010, 31(9): 1 986-1 990)
(  0) 0) |
| [7] |
齐立哲, 陈磊, 王伟, 等. 基于激光跟踪仪的机器人误差测量系统标定[J]. 制造技术与机床, 2012(10): 90-94 (Qi Lizhe, Chen Lei, Wang Wei, et al. The Calibration for Industrial Robot's Position Error Measuring System Based on the Laser Tracker[J]. Manufacturing Technology and Machine Tool, 2012(10): 90-94)
(  0) 0) |
| [8] |
陈义, 沈云中. 非线性三维基准转换的稳健估计[J]. 大地测量与地球动力学, 2003, 23(4): 49-53 (Chen Yi, Shen Yunzhong. Robust Estimation of Three Dimensional Nonlinear Datum Transformation[J]. Journal of Geodesy and Geodynamics, 2003, 23(4): 49-53 DOI:10.3969/j.issn.1671-5942.2003.04.010)
(  0) 0) |
| [9] |
潘国荣, 赵鹏飞. 基于空间向量的三维基准转换模型[J]. 大地测量与地球动力学, 2009, 29(6): 79-82 (Pan Guorong, Zhao Pengfei. 3D Datum Transformation Model Based on Space Vector[J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 79-82)
(  0) 0) |
| [10] |
潘国荣, 周跃寅. 两种坐标系转换计算方法的比较[J]. 大地测量与地球动力学, 2011, 31(3): 58-62 (Pan Guorong, Zhou Yueyin. Comparison between Two Ways of Calculation of Coordinate Transfer[J]. Journal of Geodesy and Geodynamics, 2011, 31(3): 58-62)
(  0) 0) |
| [11] |
郭迎钢, 李宗春, 何华, 等. 三维坐标转换公共点最优权值的单纯形搜索算法[J]. 测绘学报, 2020, 49(8): 1 004-1 013 (Guo Yinggang, Li Zongchun, He Hua, et al. Simplex Search Algorithm for Optimal Weights of Common Points in Three-Dimensional Coordinate Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(8): 1 004-1 013)
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44


