2. 中建新疆建工(集团)有限公司西北分公司,西安市科技西路2528号,710086
区域参考框架是全球参考框架的加密和延伸,选择合适的平差基准对区域参考框架的建立和维持至关重要。利用GNSS技术建立和维持区域参考框架时,通常选择区域内部及周边均匀分布的IGS站作为起算点,并利用国际地球自转服务(International Earth Rotation Service, IERS)组织发布的国际地球参考框架(international terrestrial reference frame, ITRF)的坐标和线性速度成果,计算指定历元下的IGS站坐标作为先验坐标。然而,随着IGS站的长期运行,受地壳变化、地震和更换天线等因素影响,该方法计算的ITRF坐标常包含粗差[1]。因此,使用合适的基准约束消除或削弱起算点的粗差对保证框架维持成果的可靠性至关重要。
GNSS自由网是秩亏的,为获取可靠的框架成果,需要附加合适的基准约束条件转换到指定的参考框架[2]。常用的GNSS网平差方法有参数加权法和最小约束法。参数加权法是给予起算点坐标指定的约束,将整网结果强制约束到由起算点构成的坐标框架,是我国工程领域应用最普遍的方法[3],大多数测绘工程均采用该方法实现全球框架到区域框架的转换工作。然而,该方法需要给予起算点合适的坐标精度,实践中常凭经验给予坐标约束。当起算站点存在粗差时,会造成网形扭曲,严重影响待解点的定位结果[3-4]。最小约束法是利用相似变换方法构建起算点网形与自由网网形最优符合的约束条件[4],该方法附加的条件数为秩亏数,能有效保留控制网本身的基准信息。但当起算点坐标存在粗差时,仍然会造成整网存在系统误差。采用IGS官网发布的站点瞬时框架坐标,对其进行参数约束平差是最常用且能有效消除粗差影响的框架维持方法[5]。然而,该方法依赖于IGS官网发布的瞬时框架坐标成果,会大大影响框架维持的时效性。
在已有研究基础上,为解决起算点粗差对框架成果的影响,本文提出基于Helmert转换模型的基准约束方法。首先对自由网解进行最小约束平差,然后利用Helmert转换法识别并剔除存在粗差的起算点,最后利用最优起算点的先验坐标构建相似变换约束条件,平差得到GNSS框架网的坐标成果。同时设计对比实验,采用IGS站ITRF2014坐标分别构建参数加权约束、最小约束、顾及IGS站先验坐标误差的Helmert模型约束解算中国大陆构造环境监测网络(下文简称陆态网)框架成果,分析成果的精度和一致性,以验证本文所提算法的性能。
1 区域参考框架的基准约束方法 1.1 参数加权约束法现代大地测量中不存在完全未知的参数,在确定GNSS网的起算基准时,通常采用全球IGS站的先验坐标和精度,平差数学模型如下[2]:
| $\left\{\begin{array}{l} E(\boldsymbol{L})=\underset{n \times t}{\boldsymbol{A}}\ \underset{t \times 1}{\boldsymbol{X}} \\ D(\boldsymbol{L})=\mathit{\boldsymbol{\varSigma}}=\sigma_0^2 \boldsymbol{Q}=\sigma_0^2 \boldsymbol{P}^{-1} \\ D(\boldsymbol{X})=\mathit{\boldsymbol{\varSigma}}_X=\sigma_0^2 \boldsymbol{Q}_X=\sigma_0^2 \boldsymbol{P}_X^{-1} \\ E(\boldsymbol{X})=\boldsymbol{\mu}_X \\ \mathit{\boldsymbol{\varSigma}}_{X L}=0 \end{array}\right.$ | (1) |
式中,L为观测值,E(L)为L的期望值,D(L)为L的方差,μX为参数X的先验值,ΣX为参数X的先验方差-协方差阵,QX为参数X的先验单位协方差矩阵,PX为参数X的先验单位权阵,ΣXL为X与L的协方差且为正定矩阵。取X的近似坐标为X0=μX,列出误差方程:
| $\boldsymbol{V}=\boldsymbol{A} \hat{\boldsymbol{x}}-\boldsymbol{l}, \boldsymbol{l}=\boldsymbol{A} \boldsymbol{X}_0-\boldsymbol{L}$ | (2) |
式中,V为观测值改正数,
按最小二乘原理
| $\left\{\begin{array}{l} \hat{\boldsymbol{x}}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}+\boldsymbol{P}_X\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{l}=\left(\boldsymbol{N}+\boldsymbol{P}_X\right)^{-1} \boldsymbol{W} \\ \boldsymbol{Q}_{\dot{x}}=\left(\boldsymbol{N}+\boldsymbol{P}_X\right)^{-1}\left(\boldsymbol{Q}+\boldsymbol{A} \boldsymbol{Q}_X \boldsymbol{A}^{\mathrm{T}}\right)\left(\boldsymbol{N}+\boldsymbol{P}_X\right)^{-1} \end{array}\right.$ | (3) |
式中,
考虑到
| $\boldsymbol{Q}_{\hat{X}}=\left(\boldsymbol{N}+\boldsymbol{P}_X\right)^{-1}=\boldsymbol{Q}_X-\boldsymbol{Q}_{\dot{x}}$ | (4) |
式中,
参数加权法能解决GNSS自由网平差的秩亏问题,可获得网的绝对定位结果。在实际使用中,究竟要给予何种程度的约束,在很大程度上需要凭经验确定,尤其是当起算点坐标中存在粗差时,会导致整个网形的扭曲,严重影响框架成果的可靠性[6]。
1.2 最小约束法最小约束的含义是在处理观测量得到点位坐标时,仅包含定义其自身参考框架的必需数据或约束[6]。因此,需要在式(2)上附加秩亏数d(d=μ-t)个约束条件,其中,μ为待解参数个数,t为必要观测个数。通常在GNSS网中,确定两个参考框架的转换关系是利用7个参数构成的相似转换模型进行描述[7],即
| $\boldsymbol{X}_2=\boldsymbol{X}_1+\boldsymbol{D} \boldsymbol{\theta}$ | (5) |
式中,X1、X2分别为两个坐标系中的坐标;θ为转换参数,包括3个平移参数、1个尺度参数和3个旋转参数;D由基准点站坐标(…, x0i, y0i, z0i,…)构成,1<i<n,n为点位数目,D具体形式可表示为[7]:
| $\boldsymbol{D}=\left[\begin{array}{ccccccc} \cdot & \cdot & . & . & . & \cdot & \cdot \\ 1 & 0 & 0 & x_0^i & 0 & z_0^i & -y_0^i \\ 0 & 1 & 0 & y_0^i & -z_0^i & 0 & x_0^i \\ 0 & 0 & 1 & z_0^i & y_0^i & -x_0^i & 0 \\ . & . & . & . & . & . & . \end{array}\right]$ | (6) |
已知两个坐标系下3个以上的公共点,利用最小二乘法可解得 θ:
| $\boldsymbol{\theta}=\left(\boldsymbol{D}^{\mathrm{T}} \boldsymbol{P}_X \boldsymbol{D}\right)^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{P}_X\left(\boldsymbol{X}_2-\boldsymbol{X}_1\right)$ | (7) |
设B=(DTPXD)-1DTPX,式(7)可转化为:
| $\boldsymbol{\theta}=\boldsymbol{B}\left(\boldsymbol{X}_2-\boldsymbol{X}_1\right)$ | (8) |
为消除式(2)的秩亏问题,附加约束如下:
| $\boldsymbol{B}\left(\hat{\boldsymbol{X}}-\boldsymbol{X}_0\right)=0, \left(\mathit{\boldsymbol{\varSigma}}_\theta\right)$ | (9) |
上式的条件数等于式(2)的秩亏数;Σθ为对角矩阵,对角线为转换参数的方差。通常选择的点位均为稳定站点,已知点坐标值准确,因此转换参数的方差较小,即可实现相似变换约束。
| $\left(\boldsymbol{B}^{\mathrm{T}} \mathit{\boldsymbol{\varSigma}}_\theta^{-1} \boldsymbol{B}\right)\left(\hat{\boldsymbol{X}}-\boldsymbol{X}_0\right)=0$ | (10) |
因此,附加最小约束的法方程为:
| $\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}+\boldsymbol{B}^{\mathrm{T}} \mathit{\boldsymbol{\varSigma}}_\theta^{-1} \boldsymbol{B}\right) \hat{\boldsymbol{x}}=\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{l}+\left(\boldsymbol{B}^{\mathrm{T}} \mathit{\boldsymbol{\varSigma}}_\theta^{-1} \boldsymbol{B}\right) \boldsymbol{x}_0$ | (11) |
式中,x0为转换点的坐标差。合并式(10)和(11),得:
| $\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}+\boldsymbol{B}^{\mathrm{T}} \mathit{\boldsymbol{\varSigma}}_\theta^{-1} \boldsymbol{B}\right) \hat{\boldsymbol{x}}=\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{l}$ | (12) |
由式(12)可知,相似变换约束实质上是将待定点的控制网转换到已知点所在的框架下。因为最小约束法附加的条件数等于法方程的秩亏数,因此不干扰控制网本身的基准信息。该方法可为秩亏自由网提供充分必要的起算条件,平差结果不改变由观测信息所确定的内在网形,可最大限度地保留观测精度[8]。
2 Helmert转换基准约束方法由于受地壳变化、地震、更换天线等因素影响,基准点可能存在粗差,这种粗差在解算前可能并不清楚。起算点的坐标粗差会扭曲网平差结果,引起观测网的变形[9]。本文提出的Helmert转换法可以有效剔除存在粗差的起算点,并实现平差后网形与自由网网形的最佳符合。Helmert转换法的具体解算流程如图 1所示。其中,Helmert相似变换模型为[7]:
| $\begin{aligned} & {\left[\begin{array}{c} X_1 \\ Y_1 \\ Z_1 \end{array}\right]=\left[\begin{array}{c} T_X \\ T_Y \\ T_Z \end{array}\right]+\left(1+T_S\right) \cdot} \\ & {\left[\begin{array}{ccc} 1 & R_Z & -R_Y \\ -R_Z & 1 & R_X \\ R_Y & -R_X & 1 \end{array}\right]\left[\begin{array}{l} X_0 \\ Y_0 \\ Z_0 \end{array}\right]} \end{aligned}$ | (13) |

|
图 1 Helmert转换法网平差流程 Fig. 1 Flow chart of network adjustment by Helmert conversion method |
式中,TX、TY、TZ为3个平移参数,RX、RY、RZ为3个旋转参数,TS为尺度参数。利用IGS站先验坐标构建的最小约束条件,平差得到整网结果,即(X0, Y0, Z0)、(X1, Y1, Z1)均为已知量,建立7个转换参数的误差方程:
| $\begin{array}{c} & \boldsymbol{V}=\left[\begin{array}{ccccccc} \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ 1 & 0 & 0 & x_0^i & 0 & z_0^i & -y_0^i \\ 0 & 1 & 0 & y_0^i & -z_0^i & 0 & x_0^i \\ 0 & 0 & 1 & z_0^i & y_0^i & -x_0^i & 0 \\ . & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \end{array}\right] \cdot \\ & {\left[\begin{array}{c} \hat{T}_X \\ \hat{T}_Y \\ \hat{T}_Z \\ \hat{T}_S \\ \hat{R}_X \\ \hat{R}_Y \\ \hat{R}_Z \end{array}\right]-\left[\begin{array}{c} X_1-X_0 \\ Y_1-Y_0 \\ Z_1-Z_0 \end{array}\right] } \\ & V=\boldsymbol{D} \hat{\boldsymbol{x}}-\boldsymbol{l} \end{array}$ | (14) |
式中,(x0i, y0i, z0i)为所有点的坐标,(X0, Y0, Z0)为IGS站的先验坐标,(X1, Y1, Z1)为最小约束法解算的IGS站的坐标。法方程可表示为:
| $\boldsymbol{D}^{\mathrm{T}} \boldsymbol{D} \hat{\boldsymbol{x}}=\boldsymbol{D}^{\mathrm{T}} \boldsymbol{l}$ | (15) |
利用上式计算得到转换参数
实验选取中国境内和周边15个IGS站和249个陆态网GNSS基准站,观测时间为2020-08-17~23,采用高精度GNSS数据处理软件GAMIT/GLOBK 10.70分区解算获取单天的自由网解,然后合并子区获取整个区域的单天自由网解,最终合并单天解获取周自由网解SINEX文件。SINEX文件中IGS基准站的先验坐标由IERS发布的ITRF2014框架的坐标和线性速度成果归算获取。利用GAMIT进行基线解算时,主要的控制参数设置见表 1,基线解算结果见表 2。
|
|
表 1 主要控制参数 Tab. 1 The main control parameters |
|
|
表 2 基线解算精度 Tab. 2 Baseline solution accuracy |
区域参考框架的可靠性至关重要,将其与ITRF参考框架联系起来是实现区域参考框架最有效的手段。本文采用不同的基准约束方案解算陆态网在ITRF2014框架下的坐标,利用Python编程实现3种平差方法,并构建4种基准约束条件进行整网平差。
方案1:以15个IGS站为起算点,N、E、U方向上的坐标先验精度分别为1 mm、1 mm、2 mm。
方案2:以15个IGS站构建七参数相似变换,7个参数先验精度分别为10-5 m、10-5 m、10-5 m、10-3 ppb、10-6″、10-6″、10-6″。
方案3:采用本文提出的Helmert转换法,将15个IGS站作为起算点构建相似变换,解算整网成果。利用Helmert坐标转换模型,计算IGS站的成果与先验坐标的偏差值,将误差超限最大的IGS站作为待解点,利用剩余IGS站重新构建七参数相似变换,迭代计算,直至不存在误差超限的IGS站。其中,7个参数的先验精度分别为10-5 m、10-5 m、10-5 m、10-3 ppb、10-6″、10-6″、10-6″。
方案4:以方案3中满足限差的IGS站为起算点,N、E、U方向上的坐标先验精度分别为1 mm、1 mm、2 mm。
为了验证解算结果的精度和可靠性,下载IGS官网发布的周解igs20P2119.ssc文件,提取中国境内及周边15个IGS站的坐标及解算精度作为起算基准进行整网平差。将解算的成果作为参考值,对比不同方案解算成果的精度和可靠性:
| $\left\{\begin{array}{l} \text { MEAN }=\frac{1}{N} \sum\limits_1^N\left(\boldsymbol{X}_i-\boldsymbol{X}_i^{\mathrm{ref}}\right) \\ \mathrm{RMS}=\sqrt{\frac{1}{N} \sum\limits_1^N\left(\boldsymbol{X}_i-\boldsymbol{X}_i^{\mathrm{ref}}\right)^2} \end{array}\right.$ | (16) |
式中,Xi为不同方案的站点解算成果;Xiref为参考方案的解算成果;N表示整网站点数;平均偏差MEAN可衡量不同方案的偏离程度,均方根误差RMS可衡量解算方案的成果精度和稳定性。
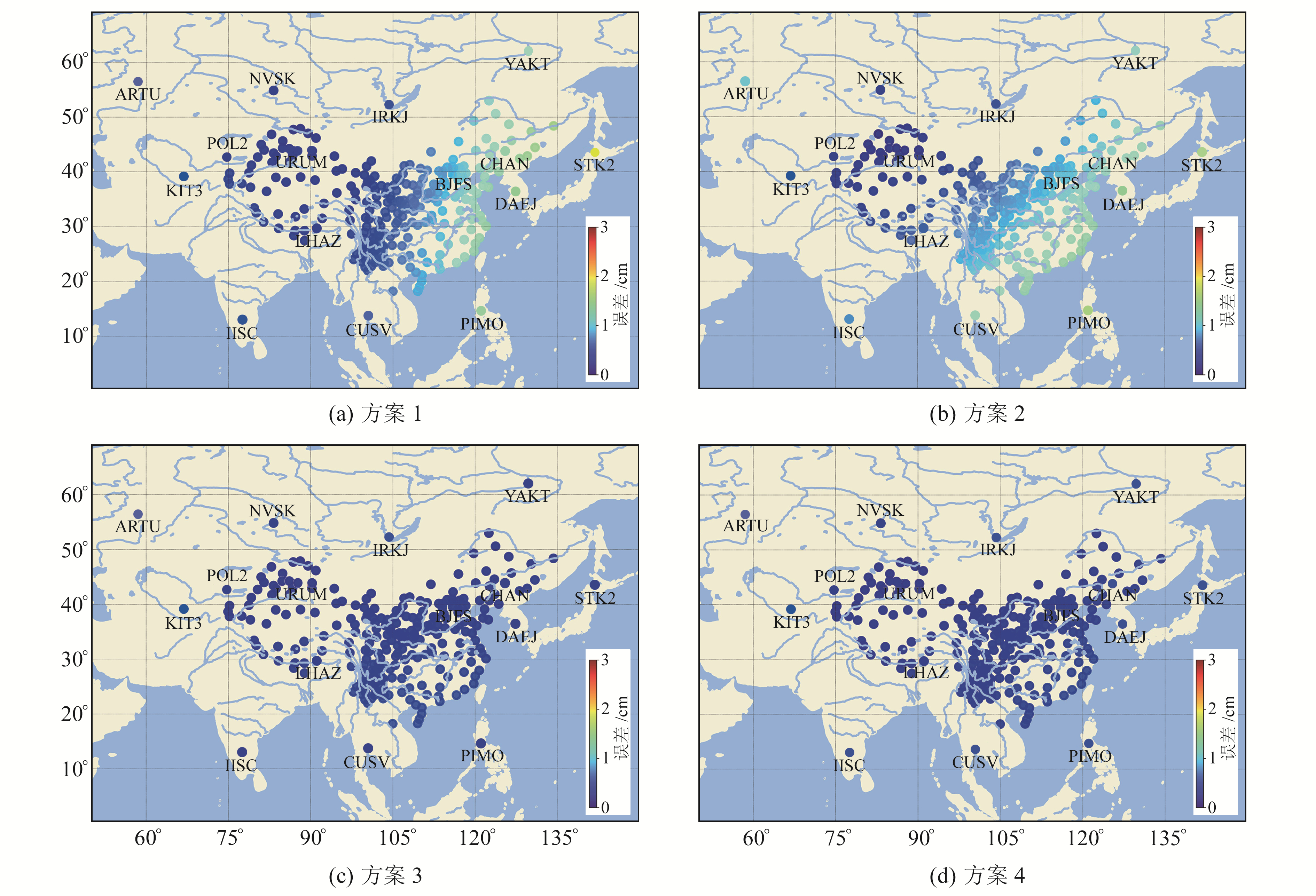
分别采用4种基准约束平差方案获取陆态网的ITRF2014框架成果,计算4种方案结果与参考值的误差值(误差的绝对值),图 2为平面方向误差值分布结果,图 3为大地高方向误差值分布结果。
|
图 2 平面解算误差分布 Fig. 2 Distribution of plane error |

|
图 3 大地高解算误差分布 Fig. 3 Distribution of ellipsoidal error |
由图 2可知,方案1和2平面坐标误差较大,方案3和4平面误差较小。方案1设定所有IGS站1 mm的平面坐标精度约束,但CHAN、DAEJ、STK2和URUM站平面的先验坐标与周解的误差超过3 cm,导致网形扭曲,且距离误差点越近,站点的误差值越大。方案2采用最小约束法,保证了解算前后网形的一致性,但起算点粗差同样会代入整网,影响平差结果。方案3解算误差分布均匀,且均优于1 cm,说明该方法可有效削弱起算点粗差对解算结果的影响。方案4与方案3解算结果相近,说明利用方案3选取的起算点的平面坐标不再包含粗差,满足1 mm先验坐标精度。
由图 3可知,方案1和4大地高误差较大,方案2和3大地高误差较小。方案1大地高误差分布不均匀,IGS站大地高误差较大,陆态网站大地高误差较小。方案2大地高误差分布均匀,IGS站和陆态网站大地高误差均较小,说明最小约束法能有效削弱大地高方向的误差。方案3大地高误差分布均匀且最小,说明Helmert转换法能削弱粗差对平差结果的影响,是最优的区域框架基准约束方法。方案4中部分IGS站大地高误差较大,且中国东部的陆态网站大地高误差较大。
为进一步分析不同方案定位结果的精度和可靠性,分别统计4种基准约束平差方案的站点误差,表 3(单位cm)和表 4(单位cm)分别为15个IGS站和249个陆态网站点坐标的误差统计结果(最大值为绝对值的最大值)。
|
|
表 3 IGS基准站坐标误差 Tab. 3 Positioning error of IGS reference stations |
|
|
表 4 陆态网基准站坐标误差 Tab. 4 Positioning error of reference stations in Crustal Movement Observation Network of China |
由表 3和表 4可知,方案3中IGS站和陆态网站的解算误差均优于1 cm,各方向RMS值均优于5 mm,是4种方案中的最优方案。方案1中IGS站的误差较大,原因为部分站点存在未知的粗差,因此给定的先验精度不合理会造成网形扭曲。方案2相对于方案1大地高方向误差较小,说明最小约束法能在一定程度上降低网形扭曲造成的误差。方案3利用Helmert转换法可有效识别并剔除存在粗差的站点,同时利用最小约束法确保解算前后网形的一致性,实现整网平差成果的高精度和高可靠性。方案4相对于方案3大地高方向误差较大,其原因为剔除的IGS站大地高方向限差为3 cm,当选定的IGS站采用2 mm精度约束时,高程方向的粗差同样会造成网形扭曲。
由表 2可知,基线解算结果满足mm级精度,保持网形的情况下引入合适的基准约束,即可获取高精度的框架成果。因此,解算前后单位权方差的一致性与网形变化强相关。为分析不同解算方案对网形的影响,分别对解算前后单位权方差进行卡方检验(χ2)。卡方检验的相关系数可表征两个变量之间的相关程度,相关系数绝对值越大,相关性越强;反之,相关系数越接近于0,相关度越弱。相关强度可以通过表 5进行判断[10]。
|
|
表 5 相关系数 Tab. 5 Correlation coefficient |
由表 6可知,方案3的χ2值最小,说明解算前后单位权方差变化小,即网形一致性最好,实现了解算前后站点间相对关系不变。方案1和方案4的χ2值超过0.4,说明解算前后单位权方差变化大,给定的基准约束造成网形变化较大。采用方案3解算时,利用Helmert模型计算出未超限的11个IGS站的先验坐标到平差结果的转换参数,结果见表 7。
|
|
表 6 χ2检验结果 Tab. 6 The results of chi-square test |
|
|
表 7 Helmert转换法的转换参数 Tab. 7 Conversion parameters of Helmert conversion method |
当起算站点先验坐标存在未知误差时,采用方案3的平差算法可以有效识别先验坐标存在较大粗差的站点。同时,最小约束平差方法可保证整网间站点相对关系的可靠性,利用转换参数吸收起算点的小粗差,获取高精度和高可靠性的区域框架成果。
4 结语为解决起算点IGS站的坐标粗差对区域框架维持的影响,本文提出基于Helmert转换法的基准约束方法。该算法基于高精度的GNSS自由网成果,利用Helmert转换模型保持解算前后网形的一致性,然后迭代计算起算点的坐标误差,实现粗差点的识别与剔除。实验结果表明,本文提出的Helmert转换法与传统的参数加权法、最小约束法相比,定位精度优于传统策略,且能有效削弱起算点坐标粗差对网形结构的影响,提高框架成果的可靠性。
致谢: 本文使用的GNSS数据为中国地震局提供的陆态网基准站观测数据,数据处理采用GAMIT/GLOBK软件,在此一并表示感谢。
| [1] |
王穗辉. 顾及起算数据误差的附加基准平差[J]. 大地测量与地球动力学, 2005, 25(1): 72-75 (Wang Suihui. Adjustment Method of Appending Datums Taking Initial Data Errors into Account[J]. Journal of Geodesy and Geodynamics, 2005, 25(1): 72-75 DOI:10.3969/j.issn.1671-5942.2005.01.014)
(  0) 0) |
| [2] |
刘根友, 郝晓光, 柳林涛. 参数约束平差法[J]. 大地测量与地球动力学, 2006, 26(4): 5-9 (Liu Genyou, Hao Xiaoguang, Liu Lintao. Method of Parameter Constraint Adjustment[J]. Journal of Geodesy and Geodynamics, 2006, 26(4): 5-9 DOI:10.3969/j.issn.1671-5942.2006.04.002)
(  0) 0) |
| [3] |
李志才, 孙占义, 张庆兰, 等. 我国CGCS2000坐标框架与全球ITRF2008框架的融合研究[J]. 测绘通报, 2016(12): 10-12 (Li Zhicai, Sun Zhanyi, Zhang Qinglan, et al. Research on Coordinate Reference Frame Fusion from Regional CGCS2000 to Global ITRF2008[J]. Bulletin of Surveying and Mapping, 2016(12): 10-12)
(  0) 0) |
| [4] |
陶本藻. 自由网平差与变形分析[M]. 武汉: 武汉测绘科技大学出版社, 2001 (Tao Benzao. Free Network Adjustment and Deformation Analysis[M]. Wuhan: Wuhan Technology University of Surveying and Mapping Press, 2001)
(  0) 0) |
| [5] |
Altamimi Z, Collilieux X, Legrand J, et al. ITRF2005: A New Release of the International Terrestrial Reference Frame Based on Time Series of Station Positions and Earth Orientation Parameters[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B9)
(  0) 0) |
| [6] |
Altamimi Z, Boucher C. The ITRS and ETRS89 Relationship: New Results from ITRF2000[C]. The EUREF Symposium, Dubrovnik, 2001
(  0) 0) |
| [7] |
Sillard P, Boucher C. A Review of Algebraic Constraints in Terrestrial Reference Frame Datum Definition[J]. Journal of Geodesy, 2001, 75(2): 63-73
(  0) 0) |
| [8] |
张勤, 黄观文, 丁晓光, 等. 顾及板块运动、稳定性和系统偏差的高精度GPS监测基准研究与实现[J]. 地球物理学报, 2009, 52(12): 3 158-3 165 (Zhang Qin, Huang Guanwen, Ding Xiaoguang, et al. Research and Realization of High-Precision GPS Datum, Considering Plate Movement, Stability and System Errors[J]. Chinese Journal of Geophysics, 2009, 52(12): 3 158-3 165)
(  0) 0) |
| [9] |
施闯, 邹蓉, 姚宜斌, 等. 基于SINEX解的数据组合及系统误差分析[J]. 武汉大学学报: 信息科学版, 2008, 33(6): 608-611 (Shi Chuang, Zou Rong, Yao Yibin, et al. Systematic Error Analysis in Data Combination Based on SINEX Solution[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6): 608-611)
(  0) 0) |
| [10] |
苗岳旺, 周巍, 田亮, 等. 基于新息χ2检测的扩展抗差卡尔曼滤波及其应用[J]. 武汉大学学报: 信息科学版, 2016, 41(2): 269-273 (Miao Yuewang, Zhou Wei, Tian Liang, et al. Extended Robust Kalman Filter Based on Innovation Chi-Square Test Algorithm and Its Application[J]. Geomatics and Information Science of Wuhan University, 2016, 41(2): 269-273)
(  0) 0) |
2. Northwest Branch of CSCEC Xinjiang Construction and Engineering Group Co Ltd, 2528 West-Keji Road, Xi'an 710086, China
 2024, Vol. 44
2024, Vol. 44


