2. 西安测绘研究所,西安市雁塔路中段1号,710054
2017年,北斗卫星导航系统开始使用北斗坐标系(Beidou coordinate system,简称BDCS)作为其专用坐标系。魏子卿等[1]、Wu等[2]采用2007年、2011年、2014年和2016年4期GPS观测数据首次建立了北斗坐标系,与国际IGS站进行全球组网,获得对准于ITRF2014框架的北斗地面监测站坐标和速度。
北斗参考框架是北斗坐标系的物理实现,许多学者围绕北斗参考框架的建立与维持展开研究:邹蓉等[3-4]提出北斗参考框架的建立与维持方案,并基于GPS数据进行一系列仿真验证;施闯等[5]利用已建成的北斗基准站观测数据,基于北斗技术建立与国际地球参考框架(ITRF)一致的国家大地坐标参考框架;魏娜等[6]基于ITRF的定义及实现方法,利用国内监测站和国际监测站来定义、精化和维持北斗参考框架,并利用GPS数据作初步分析。早期关于北斗参考框架的研究及北斗坐标系的首次实现都是采用GPS观测数据,随着BDS-3全球卫星导航系统的建成,国际ITRF框架点逐渐采用多系统接收机,至此采用北斗观测数据维持北斗参考框架的条件已具备。
北斗坐标框架由IGS参考站与国内北斗监测站全球组网解算实现,因此IGS参考站的选取对于北斗坐标框架的维持至关重要。IGS参考站的选取一般遵循连续性、稳定性、高精度和多种解原则[7]。秘金钟等[8]在以上4个原则的基础上提出平衡性原则和精度一致性原则;高乐等[9]分析数据质量,利用七参数法进行精选,使台站空间分布均匀化。格网法也是进行全球均匀选站的主要方法,能够简单、直观地获取测站的均匀分布构型,但不能兼顾站点稳定性、数据质量等因素[10]。韩德强等[10]提出基于格网控制概率下的全球测站随机优化算法,该方法可综合考虑站点几何分布、稳定性和观测质量等信息。
本文着眼于现实需求,在格网法基础上提出一种既考虑全球分布均匀性又考虑数据质量的选站方法,并利用该方法优选72个全球均匀分布的测站作为北斗坐标框架解算中的国际参考站,为北斗参考框架的维持和精化提供支撑。
1 北斗参考框架选站方法格网控制法是目前常用的参考框架选站方法,根据选取的测站数量,采用合适的经纬度网格进行划分,选取出均匀分布的测站。但格网法主要考虑测站的分布,难以兼顾测站的稳定性及数据质量等信息。本文在格网法的基础上提出一种考虑数据质量及站点位置精度的北斗参考框架选站方法,主要步骤为:1)确定测站数目;2)从ITRF2020框架中筛选能接收北斗信号的测站;3)分析数据质量(包括数据完整性、卫星可见性和多路径效应),进行站点粗选;4)确定每个测站的质量因子(综合考虑站点精度及多路径效应);5)划分格网;6)选取测站。
1.1 确定测站数目选用40~60个均匀分布的IGS参考站与国内监测站进行组网解算。考虑到数据质量及实际分布的不均匀性,本文从ITRF2020框架中优选60~70个参考站作为北斗坐标框架解算中的IGS参考站。
1.2 从ITRF2020框架中筛选出能接收北斗信号的测站截至2022-02,IGS官网的500多个IGS站中,有306个测站能接收北斗数据,其中有25个数据异常的问题测站需要进行剔除。测站需要在ITRF框架中选取,因此还应剔除不包含在ITRF2020框架中的24个测站。
1.3 测站数据质量分析表征数据质量的指标主要包括数据完整性、卫星可见性、多路径误差、信噪比、周跳比等[11-13]。本文在粗选步骤中主要考虑数据完整性、卫星可见性,在精选步骤中主要考虑多路径误差。
1.3.1 数据完整性数据完整性是可用历元和理论历元的比值,反映数据的连续情况和质量水平,数据完整性的比值越大数据质量越好。一般来说,数据完整性小于85%时就应该考虑优化测站的位置或周围环境。数据完整性定义为:
| $I=\frac{C}{T}$ | (1) |
式中,C、T分别为可用历元和理论历元。
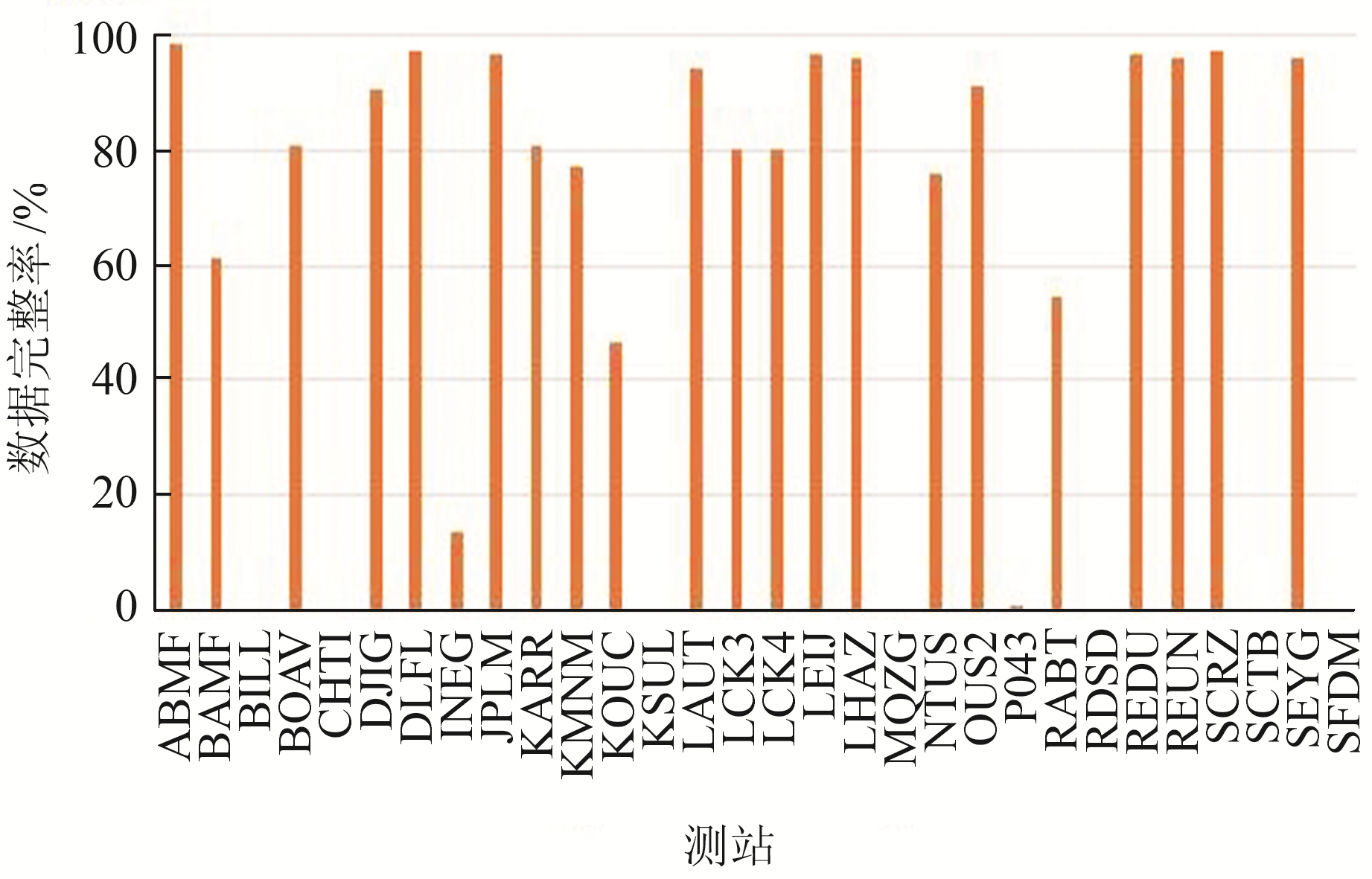
表 1为数据量统计,图 1为部分测站的数据完整率统计。分析结果表明,数据完整性大于82.2%(数据量大于等于300 d)的测站有207个,数据完整性大于90.4%(数据量大于等于330 d)的测站有192个。本步骤中需将数据量小于300 d的测站剔除。
|
|
表 1 数据量统计 Tab. 1 Statistics of data volume |
|
图 1 部分测站数据完整性 Fig. 1 Data integrity of some stations |
利用GNSS进行定位时,要同时观测4颗以上的卫星,进行坐标框架解算时需要剔除卫星可见性较差的测站。此外还可能有个别测站接收不到北斗信号,也需剔除。
图 2为CAS1站和CEDU站的卫星可见性,其中CAS1测站只能接收C02、C03、C04卫星信号,CEDU测站则能接收30颗北斗卫星信号,表 2为测站平均卫星可见数统计结果。本步骤中删除平均卫星可见数小于5的13个测站。

|
图 2 CAS1站和CEDU站卫星可见性 Fig. 2 Satellite visibility of CAS1 station and CEDU station |
|
|
表 2 平均卫星可见数统计 Tab. 2 Statistics of average number of visible satellites |
多路径误差通常反映周围环境其他因素对信号传播的影响,多路径误差越小,说明抗多路径能力越强。多路径误差通常可以通过伪距和载波相位观测值组合求得,即
| $M_k=P_k-L_i-\beta\left(L_i-L_j\right)=P_k+\alpha L_i+\beta L_j$ | (2) |
| $\left\{\begin{array}{l} \alpha=-\frac{\left(f_j^2+f_k^2\right) f_i^2}{\left(f_i^2-f_j^2\right) f_k^2} \\ \beta=\frac{\left(f_i^2+f_k^2\right) f_i^2}{\left(f_i^2-f_j^2\right) f_k^2} \end{array}\right.$ | (3) |
式中,Mk为伪距多路径误差,Pk为双频伪距观测值,Li和Lj为双频载波相位观测值,fi、fj和fk为载波频率,k、i、j为频率编号。
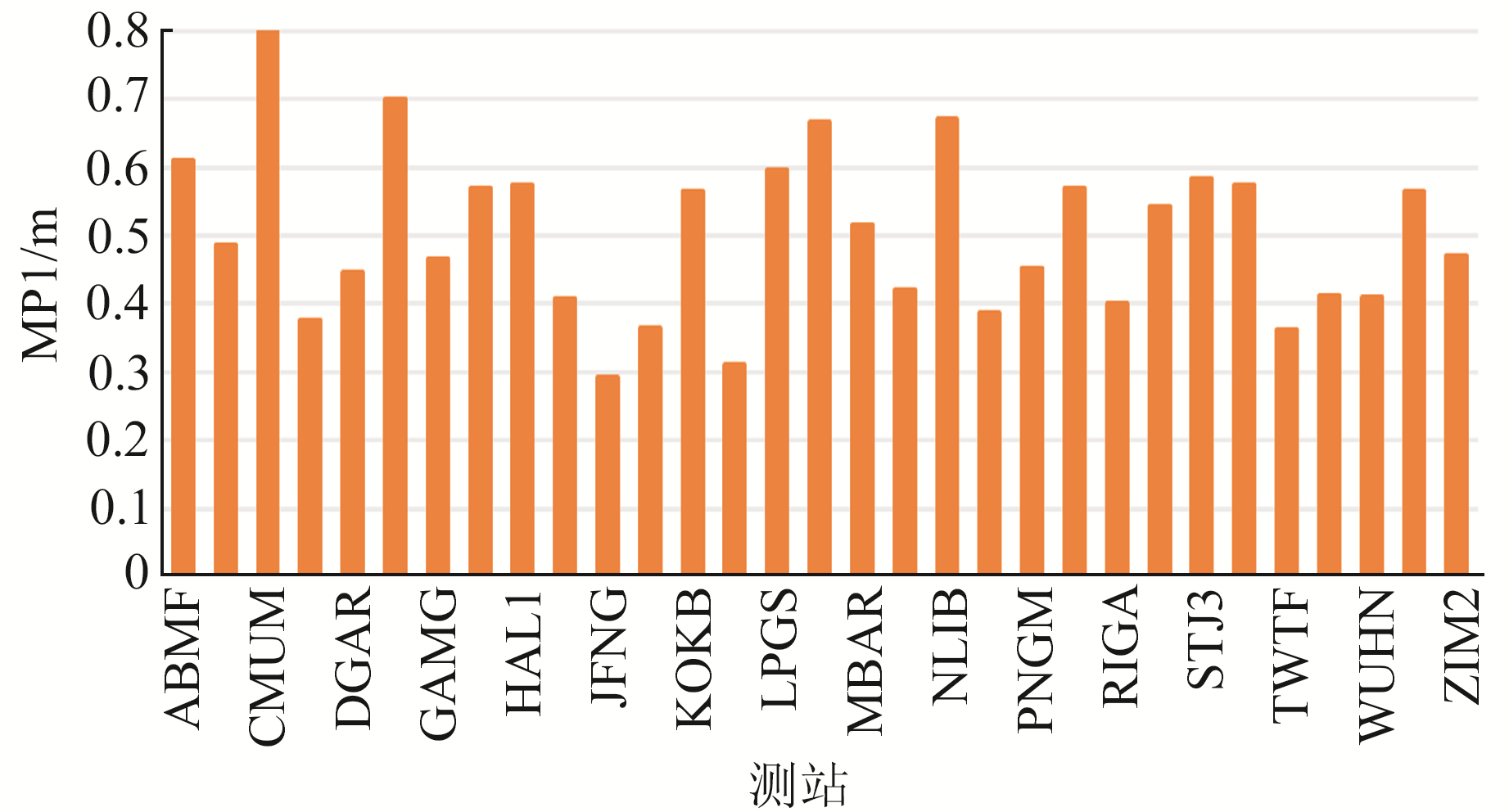
图 3为部分测站多路径误差MP1(B1I频段)分析结果,表 3为B1I、B2I、B3I频段多路径误差平均值统计。多路径误差小于0.5 m的测站有174个,多路径误差大于0.5 m的测站有20个。考虑到测站分布情况,本步骤不对测站进行剔除,在后续分析中综合考虑站点位置精度、多路径误差及均匀性对测站进行筛选。
|
图 3 部分测站多路径误差MP1 Fig. 3 Multipath error MP1 of some stations |
|
|
表 3 B1I、B2I、B3I频段多路径误差平均值统计 Tab. 3 Statistics of average multipath error in B1I, B2I and B3I frequency bands |
格网法的基本思路是:首先采用经纬度网格把众多离散的点分别划分在不同区域;然后根据选取的测站数量,使用一个相对合适的经纬度网格划分全球区域;最后在格网中选取一定数量的点[12]。经纬度的格网数为:
| $\text { num }=\left\lceil\frac{360}{10 n} \times \frac{180}{10 n}\right\rceil, n=1, 2, 3, \cdots$ | (4) |
式中,
划分网格后,确定每个格网和范围及每个点所属的网格。由于测站在全球内分布非常不均匀,欧洲地区测站非常密集,非洲、亚洲北部和海洋上测站极少,因此每个格网中测站数量不一样。当格网中有多个点时,随机或人为选取测站都很难综合考虑测站位置、质量、站点稳定性等因素。
1.5 根据站点质量因子选站考虑到传统格网法的弊端,参考文献[12]中的思路,当格网中有多个测站时,考虑格网中测站的数据质量及站点精度,确定每个测站的质量因子。质量因子计算公式为[12]:
| $G_j^i=\frac{b \sigma_{0 j}^{i 2}}{\sum\limits_{j=1}^k \sigma_{0 j}^{i 2}}+\frac{d \mathrm{MP}_j^i}{\sum\limits_{j=1}^k \mathrm{MP}_j^i}$ | (5) |
式中,Gji为第i个格网中第j个站点的质量因子;σ0ji2=σx2+σy2+σz2,其中σx、σy、σz分别为站点坐标在x、y、z方向上的中误差;k为第i个格网中的站点数;MPji为第i个网格中第j个站点的多路径误差值;b、d为经验值,均取值1。
选站的主要思路为:当格网内有一个测站时,选取该测站作为格网的最优测站;当格网内有多个测站时,选取测站质量因子最小的测站作为该格网的最优测站。
2 框架点选择结果粗选过程中已经剔除了问题测站、不在ITRF2020框架中的测站、平均卫星可见数小于5的测站、2021年数据量低于300 d的测站,经过粗选后可供筛选的测站为194个。根据测站选取算法及思路,最终选择72个测站,如图 4所示。

|
图 4 框架点选取结果 Fig. 4 Results of chosen reference sites |
选择的框架点精度信息及数据质量信息如表 4所示,表 5为多路径误差、数据量及精度信息的最大值与最小值。
|
|
表 4 部分IGS框架点的数据质量及精度信息 Tab. 4 Dataquality and accuracy information tables of some chosen IGS reference sites |
|
|
表 5 IGS框架点数据质量及精度信息统计 Tab. 5 Statistics of data quality and accuracy information of the chosen IGS reference sites |
本文围绕北斗参考框架维持与精化的现实需求以及北斗卫星导航系统全球组网的契机,研究北斗坐标框架解算中的IGS参考站选站方法。首先从ITRF2020参考框架中筛选能接收北斗数据的站点,从数据完整性、卫星可见性和多路径误差等方面分析数据质量,并设定相应的标准进行站点粗选;然后在粗选站点的基础上对格网法进行改进,提出一种能够综合考虑均匀性、数据质量和站点稳定性的选站方法;最后利用该方法在ITRF2020参考框架中优选72个测站作为北斗坐标框架解算中的IGS参考站,可为后期北斗参考框架的维持与精化提供参考。
| [1] |
魏子卿, 吴富梅, 刘光明. 北斗坐标系[J]. 测绘学报, 2019, 48(7): 805-809 (Wei Ziqing, Wu Fumei, Liu Guangming. The Beidou Coordinate System[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 805-809)
(  0) 0) |
| [2] |
Wu F M, Wei Z Q, Ming F, et al. The First Realization of BeiDou Coordinate System and Its Assessment[J]. Journal of Surveying Engineering, 2021, 147(2)
(  0) 0) |
| [3] |
邹蓉, 刘晖, 魏娜, 等. COMPASS地球参考框架的建立和维持[J]. 武汉大学学报: 信息科学版, 2011, 36(4): 431-436 (Zou Rong, Liu Hui, Wei Na, et al. Establishment and Maintenance of the Compass Terrestrial Reference Frame[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 431-436)
(  0) 0) |
| [4] |
邹蓉, 刘晖, 杨蜀江. 伽利略地球参考框架对建立我国自主的地球参考框架的启示[J]. 武汉大学学报: 信息科学版, 2009, 34(11): 1 266-1 270 (Zou Rong, Liu Hui, Yang Shujiang. Inspiration of Establishing COMPASS Terrestrial Reference Frame from GTRF Realization[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11): 1 266-1 270)
(  0) 0) |
| [5] |
施闯, 魏娜, 李敏, 等. 利用北斗系统建立和维持国家大地坐标参考框架的方法研究[J]. 武汉大学学报: 信息科学版, 2017, 42(11): 1 635-1 643 (Shi Chuang, Wei Na, Li Min, et al. Approaches to Realize and Maintain National Terrestrial Reference Frame Based on BDS Data[J]. Geomatics and Information Science of Wuhan University, 2017, 42(11): 1 635-1 643)
(  0) 0) |
| [6] |
魏娜, 陈国, 蔡洪亮, 等. 北斗地球参考框架的初始实现及分析[C]. 第5届中国卫星导航学术年会, 南京, 2014 (Wei Na, Chen Guo, Cai Hongliang, et al. Compass Terrestrial Reference Frame(CTRF): Initial Realization and Analysis[C]. The 5th China Satellite Navigation Academic Annual Conference, Nanjing, 2014)
(  0) 0) |
| [7] |
程鹏飞, 成英燕. 基于GNSS的CGCS2000数据处理技术综述[J]. 武汉大学学报: 信息科学版, 2018, 43(12): 2 071-2 078 (Cheng Pengfei, Cheng Yingyan. An Overview of the CGCS2000 Coordinate Processing Technique Based on GNSS[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 071-2 078)
(  0) 0) |
| [8] |
秘金钟, 蒋志浩, 张鹏, 等. IGS跟踪站与国内跟踪站联合处理的框架点选择研究[J]. 武汉大学学报: 信息科学版, 2007, 32(8): 704-706 (Bei Jinzhong, Jiang Zhihao, Zhang Peng, et al. On Framework Sites Selection for Unite-Processing of IGS CORS and Domestic CORS[J]. Geomatics and Information Science of Wuhan University, 2007, 32(8): 704-706)
(  0) 0) |
| [9] |
高乐, 成英燕, 郑作亚, 等. GNSS数据处理中框架点的选取方法研究[J]. 大地测量与地球动力学, 2011, 31(2): 134-136 (Gao Le, Cheng Yingyan, Zheng Zuoya, et al. Study on Method for Frame Stations Chosen in GNSS Data Processing[J]. Journal of Geodesy and Geodynamics, 2011, 31(2): 134-136)
(  0) 0) |
| [10] |
韩德强, 党亚民, 薛树强, 等. GNSS卫星精密定轨全球地面基准站网随机优化算法[J]. 武汉大学学报: 信息科学版, 2019, 44(6): 799-805 (Han Deqiang, Dang Yamin, Xue Shuqiang, et al. Stochastic Optimization on Global Ground Reference Station Network for GNSS Satellite Precise Orbit Determination[J]. Geomatics and Information Science of Wuhan University, 2019, 44(6): 799-805)
(  0) 0) |
| [11] |
丁志鹏, 贺凯飞, 邱立杰, 等. 基于Anubis的北斗观测数据质量分析[J]. 大地测量与地球动力学, 2022, 42(2): 143-147 (Ding Zhipeng, He Kaifei, Qiu Lijie, et al. Quality Analysis of BDS Observation Data Based on Anubis[J]. Journal of Geodesy and Geodynamics, 2022, 42(2): 143-147)
(  0) 0) |
| [12] |
李涌涛, 李建文, 潘林, 等. 北斗三号新信号B1C和B2a观测数据质量分析评估[J]. 地球科学进展, 2018, 33(11): 1 161-1 168 (Li Yongtao, Li Jianwen, Pan Lin, et al. Quality Assessment of the Beidou-3 New Signal B1C and B2a Observation Data[J]. Advances in Earth Science, 2018, 33(11): 1 161-1 168)
(  0) 0) |
| [13] |
伊珣, 徐爱功, 唐龙江. 利用Anubis检核BDS观测数据质量[J]. 导航定位学报, 2021, 9(5): 134-141 (Yi Xun, Xu Aigong, Tang Longjiang. Quality Check of BDS Data Using Anubis[J]. Journal of Navigation and Positioning, 2021, 9(5): 134-141)
(  0) 0) |
2. Xi'an Institute of Surveying and Mapping, 1 Mid-Yanta Middle Road, Xi'an 710054, China
 2024, Vol. 44
2024, Vol. 44

