随着智能移动终端的飞速发展,基于智能终端的位置服务极大地方便了交通出行和生产工作,超过一半的手机应用程序在使用时需要访问位置信息[1],而定位精度一直是制约其满足大众广泛需求的关键问题。2016-05谷歌公司在安卓(Android Nougat)操作系统上开放了访问GNSS原始观测值的应用程序接口,包括伪距、载波相位、多普勒频移和信号噪声比(C/No)[2],极大促进了智能手机高精度定位导航研究,同时智能手机定位芯片也由接收单系统单频信号向多系统多频快速发展[3]。
在GNSS导航定位技术的发展中,为了满足用户对高精度、连续性导航定位服务的需求,国内外学者基于低成本终端的GNSS伪距和载波相位观测值的质量和特征,对低成本终端高精度实时动态定位进行了研究。文献[4]对Nexus 9智能平板终端给出信噪比定权的随机模型,测试结果表明,信噪比定权的单点定位平面精度为2.74 m,高程精度为4.56 m,比高度角定权精度提高约26%。文献[5]提出一种相位平滑位置的方法,通过相位测速约束载体历元间的位置变化,实现平滑位置噪声。文献[6]使用优化多普勒平滑模型建立常加速度模型,降低伪距测量噪声,结果表明,定位精度和连续性相比常规RTK有一定提升。文献[7]对比分析内部和外部天线接收的GNSS数据质量,使用外部天线实现了一种接近99.9%模糊度固定率的智能手机瞬时短基线RTK模型。文献[8]分析小米8终端在L5/E5a和L1/E1频率下的性能,实验表明,在短基线情况下GPS L5和L1的伪距差分定位精度分别优于1.3 m和2.1 m。文献[9]利用小米8终端上获取的GNSS原始数据分别进行双频RTK和PPP,水平方向上定位误差分别为1.17 m与2.23 m。文献[10]提出一种利用速度约束的RTD与RTK自适应切换算法,并对华为Mate40手机进行数据实测,模糊度固定率为99.67%。文献[11]分析华为P30内置的双频GNSS芯片的GNSS观测质量,修复GPS L1观测的载波相位模糊度,在静态观测5 min后三维位置误差减小4 cm。文献[12-13]利用后处理的方式处理芯片组初始相位偏差,模糊度固定时,东、北和高程方向分别可实现1.4 cm、2.2 cm和3.6 cm的定位精度。
现有研究虽能够达到较好效果,但仍缺少对各个解算过程中的抗差以及质量控制的细节分析。基于以上研究现状,本文以小米8终端和M8终端为研究对象,提出一种附加多普勒观测值抗差速度约束RTD模型和RTK自适应切换模型,充分发挥多频率信号衰减小、抗多路径能力强的优势,利用多普勒测速得到的速度作为观测值,通过速度矢量约束位置解,保证数据质量的可靠性;通过抗差估计与卡尔曼滤波相结合对较小粗差异常值进行判别,增大异常值观测方程的方差以及协方差,以降低对解算结果的影响,提高复杂环境下的定位精度。
1 多普勒测速由于接收机和卫星的相对运动导致接收的信号频率与发射时的信号频率不一致,这种频率的偏移量称为多普勒频移,即
| $ D=f_{\mathrm{r}, j}^{\mathrm{s}}-f_{j}^{s}=-\frac{1}{c} \frac{\mathrm{d} \rho}{\mathrm{d} t} f_{j}^{\mathrm{s}} $ | (1) |
式中,c为光速;ρ为卫地距;上标s和下标r分别表示卫星和接收机;
由于多普勒与伪距的变化率之间呈线性关系,而伪距变化率又体现卫星与接收机之间相对速度,所以多普勒观测值体现了包含卫星钟速、接收机钟速、对流层延迟变化和电离层延迟变化等影响的伪距变化率。多普勒测速方程为:
| $ \begin{gathered} D_{\mathrm{r}}^{\mathrm{s}}=\lambda D=\boldsymbol{e}\left(\boldsymbol{v}^{\mathrm{s}}-\boldsymbol{v}_{\mathrm{r}}\right)+ \\ c\left(\dot{t}_{\mathrm{r}}-\dot{t}^{\mathrm{s}}\right)+\dot{T}+\dot{I}+\dot{\varepsilon} \end{gathered} $ | (2) |
式中,Drs为接收机r和卫星s之间的观测矢量长度变化率,e为接收机r到卫星s方向的单位矢量,vs和vr分别为卫星与接收机的速度矢量,c为真空中光速,tr和ts分别为接收机时钟频漂和卫星时钟频漂,T为对流层延迟,I为电离层延迟,ε为其他未模型化的误差,顶标表示各个量的变化率。根据观测方程,利用最小二乘即可解算接收机速度。
2 抗差自适应卡尔曼滤波算法 2.1 观测值残差标准化卡尔曼滤波中的新息向量是指观测值和预测值的误差序列。假设动力学模型可靠,状态预测向量Xt, t-1可靠,则卡尔曼滤波中新息向量及其方差-协方差阵为:
| $ \boldsymbol{V}_{t, t-1}=\boldsymbol{H}_{t} \boldsymbol{X}_{t, t-1}-\boldsymbol{L}_{t} $ | (3) |
| $ \boldsymbol{Q}_{V_{t, t-1}}=\boldsymbol{H}_{t} \boldsymbol{Q}_{X_{t, t-1}} \boldsymbol{H}_{t}^{\mathrm{T}}+\boldsymbol{A}_{t} $ | (4) |
式中,Vt, t-1为新息向量,Ht为t时刻观测方程的系数矩阵,Lt为t时刻的观测向量,QVt, t-1为新息向量的方差-协方差阵,At为量测噪声的方差阵,QXt, t-1为状态向量协方差矩阵。
标准化残差如下:
| $ \tilde{\boldsymbol{V}}_{q}=\left|\frac{\boldsymbol{V}_{q}-\tilde{\boldsymbol{V}}}{\boldsymbol{M}_{V}}\right| $ | (5) |
式中,
对标准化残差的超限判定以及方差-协方差阵的调整,三段式函数较为实用。本文采用IGG Ⅲ函数对观测噪声方差值进行调控,公式如下:
| $ \overline{\boldsymbol{R}}_{k}=\left\{\begin{array}{l} \boldsymbol{R}_{k}, \tilde{\boldsymbol{V}}_{q} \leqslant k_{0} \\ \boldsymbol{R}_{k} \frac{\tilde{\boldsymbol{V}}_{q}}{k_{0}}\left(\frac{k_{1}-k_{0}}{k_{1}-\tilde{\boldsymbol{V}}_{q}}\right)^{2}, k_{0}<\tilde{\boldsymbol{V}}_{q} \leqslant k_{1} \\ 100000 \boldsymbol{R}_{k}, \tilde{\boldsymbol{V}}_{q}>k_{1} \end{array}\right. $ | (6) |
式中,Rk为修改后的等价观测噪声方差;Rk为观测噪声方差;k1与k0为阈值常量,本文分别选取5和1.5。
卡尔曼滤波的验后残差及其方差-协方差阵为:
| $ \boldsymbol{V}_{t, t}=\boldsymbol{A}_{t} \boldsymbol{Q}_{V_{t, t-1}}^{-1} \boldsymbol{V}_{t, t-1} $ | (7) |
| $ \boldsymbol{Q}_{V_{t, t}}=\boldsymbol{A}_{t} \boldsymbol{Q}_{V_{t, t-1}}^{-1} \boldsymbol{A}_{t}^{\mathrm{T}} $ | (8) |
卡尔曼滤波解算后,某些未在验前进行检测的观测值误差会因为残差之间的相关性污染到正常值,从而影响定位性能。采用整体残差卡方阈值以及逐个验后残差阈值双重检核方式实现差分定位精度的提升。本文对验前残差中所有粗差均进行抗差处理,正常估计;验后残差只对超出阈值的标准化残差最大值进行抗差处理,若存在粗差则再次进行量测更新,直至标准化残差均在阈值之内。
2.2 自适应因子本文基于状态不符值构造各分量自适应因子,通过构造自适应因子动态调节状态预报向量和观测向量的权矩阵,消除动力学模型预报信息与动态载体运行轨迹之间的差异,以此解决系统噪声设置不合理的问题,提高定位的可靠性。
预测状态向量各分量的不符值为:
| $ \Delta \boldsymbol{X}=\boldsymbol{X}_{k}-\boldsymbol{X}_{k, k-1} $ | (9) |
式中,ΔX为状态向量不符值,Xk为抗差后估值,Xk, k-1为k-1时刻状态预报值。自适应滤波的过程中,状态预测向量的协方差阵等于实际预测向量偏离量的方差,即
| $ \boldsymbol{Q}_{\Delta X}=\boldsymbol{Q}_{k, k-1} $ | (10) |
式中,QΔX为ΔX的方差-协方差阵,这里取QΔX=ΔXΔXT,即可求解自适应因子:
| $ \alpha=\boldsymbol{Q}_{k, k-1} / \boldsymbol{Q}_{\Delta X} $ | (11) |
式中,α为自适应因子,它可保证滤波输出噪声的不确定度与系统噪声的不确定度大致相同。
Xk, k-1的自适应协方差矩阵与Xk, k-1之间的非对角线元素为:
| $ \bar{\sigma}_{X_{k, k-1_{j}} x_{k, k-1_{j}}}=\sqrt{\alpha_{x_{k i}}} \cdot \sqrt{\alpha_{x_{k j}}} \cdot \sigma_{X_{k, k-1_{j}}} X_{k, k-1_{j}} $ | (12) |
对角线元素方差为:
| $ \bar{\sigma}_{X_{k, k-1_{j}}}^{2}=\alpha_{x_{k i}} \cdot \sigma_{X_{k, k-1_{j}}}^{2} $ | (13) |
综上所述,采用抗差自适应卡尔曼滤波估计时整体上可以用下式:
| $ \boldsymbol{X}_{k}=\left(\boldsymbol{A}_{k}^{\mathrm{T}} \overline{\boldsymbol{P}}_{k} \boldsymbol{A}_{k}+\alpha_{\bar{x}_{k}} \boldsymbol{P}_{\bar{x}_{k}}\right)^{-1}\left(\boldsymbol{A}_{k}^{\mathrm{T}} \overline{\boldsymbol{P}}_{k} \boldsymbol{L}_{k}+\alpha_{\bar{x}_{k}} \boldsymbol{P}_{\bar{x}_{k}} \overline{\boldsymbol{X}}_{k}\right) $ | (14) |
式中,Pk为观测向量等价权;PXk为预测向量权阵;Lk为观测向量,分别为其各自方差协方差阵的倒数。
3 附加多普勒速度约束的RTD定位模型相比于常规的RTD定位模型,基于抗差速度约束的RTD模型具有更加稳健的定位性能,可以有效避免“飞点”的产生。本文将多普勒观测值双差模型加入到伪距双差模型中,进行速度估计,并利用速度值更新动力学模型坐标,达到对下一历元进行约束的效果。
多普勒双差模型如下:
| $ \Delta D_{A B}^{s j}=\Delta \dot{\rho}_{A B}^{s j}+\Delta \dot{T}_{A B}^{s j}+\Delta \dot{I}_{A B}^{s j}+\Delta \dot{\varepsilon}_{P, m, A B}^{s j} $ | (15) |
式中,DABsj为观测矢量长度变化率,A、B分别代表基准站和流动站,ΔεP, m, ABsj为噪声误差,顶标表示各个量的变化率,ρ为站星间几何距离,T为对流层延迟,I为电离层延迟。
其计算模型如下:
| $ \left[ {\begin{array}{*{20}{c}} {\Delta P_{AB}^{{S_{1j}}} - \Delta \rho _{AB}^{{S_{1j}}}}\\ \vdots \\ {\Delta P_{AB}^{{S_{nj}}} - \Delta \rho _{AB}^{{S_{nj}}}}\\ {\Delta D_{AB}^{{S_{1j}}} - \Delta \dot \rho _{AB}^{{S_{1j}}}}\\ \vdots \\ {\Delta D_{AB}^{{S_{nj}}} - \Delta \dot \rho _{AB}^{{S_{nj}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {e_x^{{S_{1j}}}}&{e_y^{{S_{1j}}}}&{e_z^{{S_{1j}}}}&0&0&0\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {e_x^{{S_{nj}}}}&{e_y^{{S_{nj}}}}&{e_z^{{S_{nj}}}}&0&0&0\\ 0&0&0&{e_x^{{S_{1j}}}}&{e_y^{{S_{1j}}}}&{e_z^{{S_{1j}}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&0&0&{e_x^{{S_{1j}}}}&{e_y^{{S_{1j}}}}&{e_z^{{S_{1j}}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{l}} {{\rm{d}}x}\\ {{\rm{d}}y}\\ {{\rm{d}}z}\\ {{\rm{d}}{{\hat v}_1}}\\ {{\rm{d}}{{\hat v}_2}}\\ {{\rm{d}}{{\hat v}_3}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\Delta \varepsilon _{{P_{AB}}}^{{S_{1j}}}}\\ \vdots \\ {\Delta \varepsilon _{{P_{AB}}}^{{S_{nj}}}}\\ {\Delta \dot \varepsilon _{{P_{AB}}}^{{S_{1j}}}}\\ \vdots \\ {\Delta \dot \varepsilon _{{P_{AB}}}^{{S_{nj}}}} \end{array}} \right] $ | (16) |
| $ \boldsymbol{e}^{S_{n j}}=\left[\frac{X_{A_{0}}-X^{S_{n}}}{\rho_{0}}-\frac{X_{A_{0}}-X^{S_{j}}}{\rho_{0}} \quad \frac{Y_{A_{0}}-Y^{S_{n}}}{\rho_{0}}-\frac{Y_{A_{0}}-Y^{S_{j}}}{\rho_{0}} \quad \frac{Y_{A_{0}}-Y^{S_{n}}}{\rho_{0}}-\frac{X_{A_{0}}-Y^{S_{j}}}{\rho_{0}}\right] $ | (17) |
式中,eSnj为星间差的方向余弦,其待估分量仅为3个坐标参数,可通过多普勒测速求取增量;XA0、YA0、ZA0为3个方向测站速度近似量;XSn、YSn、ZSn为3个方向卫星速度,可由星历计算获得;dx、dy、dz为3个方向位置改正数;
单点定位解提供给该模型坐标初值,多普勒测速解算结果提供速度初值以及初始方差。由于多普勒观测值相较于伪距观测值精度要高,故多普勒观测值与伪距观测值的先验方差比设置为1∶50。该模型同时对位置与速度分量进行了估计,其模型误差矩阵为:
| $ \boldsymbol{H}_{t}=\left[\begin{array}{cc} \boldsymbol{q}_{1} \Delta t+\frac{1}{3} \boldsymbol{q}_{2} \Delta t^{3} & \frac{1}{2} \boldsymbol{q}_{2} \Delta t^{2} \\ \frac{1}{2} \boldsymbol{q}_{2} \Delta t^{2} & \boldsymbol{q}_{2} \Delta t \end{array}\right] $ | (18) |
式中,Ht为该历元时刻的模型误差矩阵,Δt为历元时刻之差,q1与q2分别为位置和系统噪声的谱密度矩阵。
4 附加多普勒速度约束的RTK定位模型与自适应切换RTK观测模型采用与RTD相同的抗差算法,常规RTK解算时应用各系统各频段的载波与伪距双差观测方程一同参与解算,观测方程中观测量并没有直接与速度和加速度分量相关,因此要用伪距获取这两种分量。由于低成本终端大多数在运动状态下进行GNSS定位,且采样间隔通常为1 s,进行RTK定位时需要更准确的预测模型,所以采用常加速度模型,短基线情况下其待估参数向量为:
| $ \begin{aligned} \Delta \mathit{\boldsymbol{X}} =& \left[ {\begin{array}{*{20}{c}} x&y&z&{x'}&{y'}&{z'}&{x''}&{y''}&{z''} \end{array}} \right.\\ & \left.\Delta N_{1} \quad \Delta N_{2} \quad \cdots \cdot \Delta N_{n}\right] \end{aligned} $ | (19) |
式中,x、y、z为低成本终端坐标,x′、y′、z′为移动速度,x″、y″、z″为运动加速度,ΔNi为单差模糊度。
计算运动状态为:
| $ \left[\begin{array}{c} X_{t+1} \\ \dot{X}_{t+1} \\ \ddot{X}_{t+1} \end{array}\right]=\left[\begin{array}{ccc} \boldsymbol{I} & \boldsymbol{I} \Delta t & \frac{1}{2} \Delta t^{2} \boldsymbol{I} \\ & \boldsymbol{I} & \boldsymbol{I} \Delta t \\ & & \boldsymbol{I} \end{array}\right] \cdot\left[\begin{array}{l} X_{t} \\ \dot{X}_{t} \\ \ddot{X}_{t} \end{array}\right]+\boldsymbol{M}_{t} $ | (20) |
式中,I为单位阵;Mt为系统噪声矩阵,其对应位置与速度分量的位置为0,常规情况下加速度的系统噪声被视作白噪声过程,具有常量方差σa2,协方差阵为:
| $ \sum \boldsymbol{M}_{t}=\boldsymbol{\sigma}_{a}^{2}\left[\begin{array}{ccc} \frac{\Delta t^{4}}{20} & \frac{\Delta t^{3}}{8} & \frac{\Delta t^{2}}{6} \\ \frac{\Delta t^{3}}{8} & \frac{\Delta t^{2}}{3} & \frac{\Delta t}{2} \\ \frac{\Delta t^{2}}{6} & \frac{\Delta t}{2} & 1 \end{array}\right] $ | (21) |
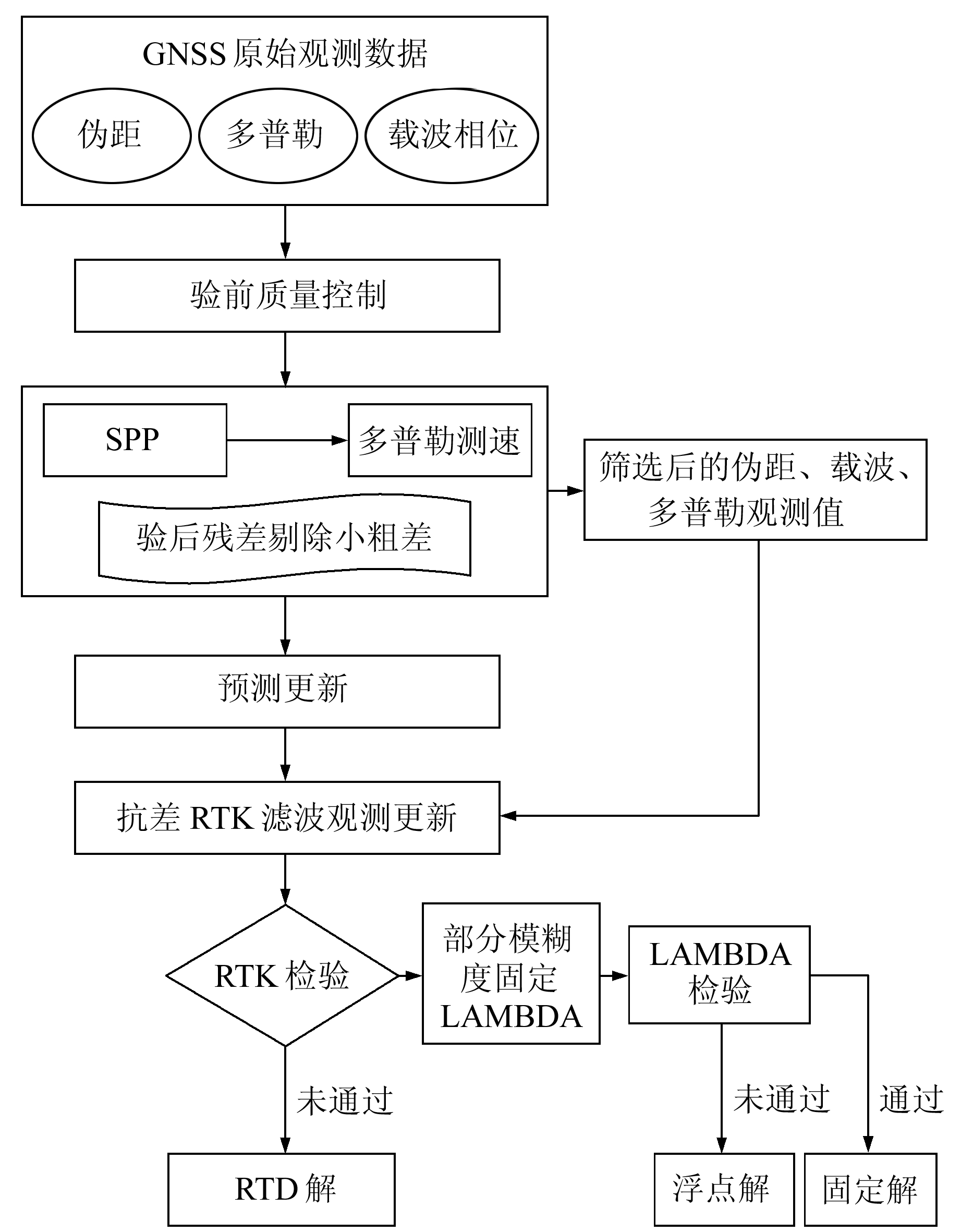
将上述多普勒观测方程同时加入到RTK解算过程中,采用伪距观测方式估计加速度分量,以增强定位结果的稳定性。由于在复杂情况下低成本GNSS终端很难一直保证RTK定位解的有效性,而RTD定位结果正确性较高,故在RTK定位结果失败时,采用抗差速度约束的RTD结果代替,以此保证定位的连续性。同时在RTK定位失败再次重新初始化时,为加快收敛速度仅将模糊度与加速度参数及其方差重新初始化,位置与速度参数及其方差直接采用抗差速度约束RTD结果。其定位模式切换流程如图 1所示。
|
图 1 算法流程 Fig. 1 Architecture of the algorithm |
本文采用小米8终端与泰瑄科技原点M8终端,通过静态和动态实验来验证所提出的抗差速度约束算法差分定位的准确性以及定位精度。静态实验中,测试环境选择在一侧高楼遮挡环境下进行,将两款设备分别放置在预先设置好的已知精确坐标的位置,分别观测一组静态数据。动态实验中,将智能终端同攀达(Panda)一体化接收机绑缚在一起,在辽宁某高校操场和花园分别进行无遮挡和部分遮挡动态实验,以攀达接收机作为坐标精确值,通过对比智能终端的计算坐标与攀达接收机坐标差值来检验定位精度。
5.1 静态RTD图 2给出小米8和M8两种终端在辽宁某高校测绘楼顶进行无遮挡静态RTD实验在东、北、高程方向的误差序列。

|
图 2 小米8终端与M8终端RTD误差序列与抗差速度约束RTD误差序列 Fig. 2 RTD error sequences with and without anti-differential velocity constrain of Mi 8 and M8 receivers |
由图 2可知,两款低成本GNSS终端平面方向大部分误差在10 m内波动,高程方向最大误差可达18 m。经过上文所述的抗差速度约束RTD算法改正后,其定位结果有明显改善,小米8终端的定位误差明显降低,平面误差保持在3 m以内,高程误差在4 m以内,对多路径误差的干扰进行了有效限制;M8低成本接收机的精度也有较大提高,定位误差大部分在3 m以内。
表 1(单位m)给出小米8和M8两种终端在静态模式常规RTD和抗差速度约束RTD的均方根(root-mean-square,RMS)定位结果。由表可知,小米8终端抗差速度约束RTD误差在东、北方向上分别约提升1.7 m、1.4 m,高程方向提升约2.7 m;M8低成本接收机本身的精度不低,所以精度提升效果不如小米8终端的明显,在平面方向约有0.3 m提升,高程方向提升约有0.9 m。
|
|
表 1 静态模式GNSS智能终端RTD RMS结果 Tab. 1 Static mode GNSS intelligent terminal RTD RMS results |
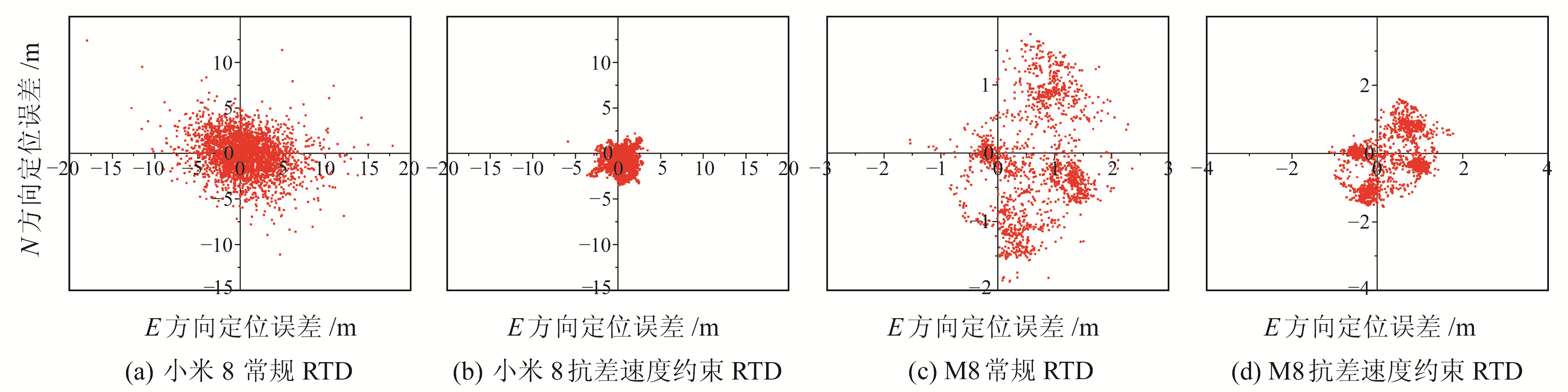
图 3给出了小米8和M8两种终端高校操场的RTD定位轨迹,定位轨迹中绿色点位为攀达专业接收机解算结果,黄色点位为常规RTD解算结果,红色点位为抗差速度约束RTD结果。图 4给出小米8和M8两种终端在操场RTD定位的平面误差。

|
图 3 智能移动终端操场RTD定位轨迹 Fig. 3 RTD positioning track of mobile intelligent terminal playground |
|
图 4 小米8终端和M8终端操场RTD定位平面误差 Fig. 4 Plane error chart of RTD positioning of Mi 8 and M8 receivers in playground |
由图 3的轨迹可知,小米8终端测试的动态常规RTD数据结果与参考点位有较大波动,操场测试的常规RTD定位解算结果没有形成轨迹,平面方向的部分点位误差达到15 m;M8终端的RTD定位解算效果优于小米8终端。
由图 4可知,小米8终端常规RTD平面方向定位误差大部分在10 m以内,使用抗差速度约束RTD模型后严重的“飞点”大幅减少,东、北方向的大部分点位的定位精度可保证在4 m以内,M8终端东、北方向的大部分点位的定位精度可保证在2 m以内。
表 2(单位m)给出小米8和M8两种终端在动态模式下常规RTD和抗差速度约束RTD的RMS定位结果。由表可知,两种智能终端在2种不同场景下抗差速度约束RTD的平面误差RMS值均在1 m左右;小米8终端的抗差速度约束RTD东方向精度提升1.03 m,北方向精度提升1.51 m,平面误差RMS值为1.55 m,相较于常规RTD有1.81 m的精度提升;M8终端的抗差速度约束RTD东方向精度提升0.39 m,北方向精度提升0.38 m,平面误差RMS值为0.74 m,相较于常规RTD有0.77 m的精度提升。
|
|
表 2 GNSS智能终端操场RTD RMS结果 Tab. 2 RTD RMS results of GNSS intelligent terminals in playground |
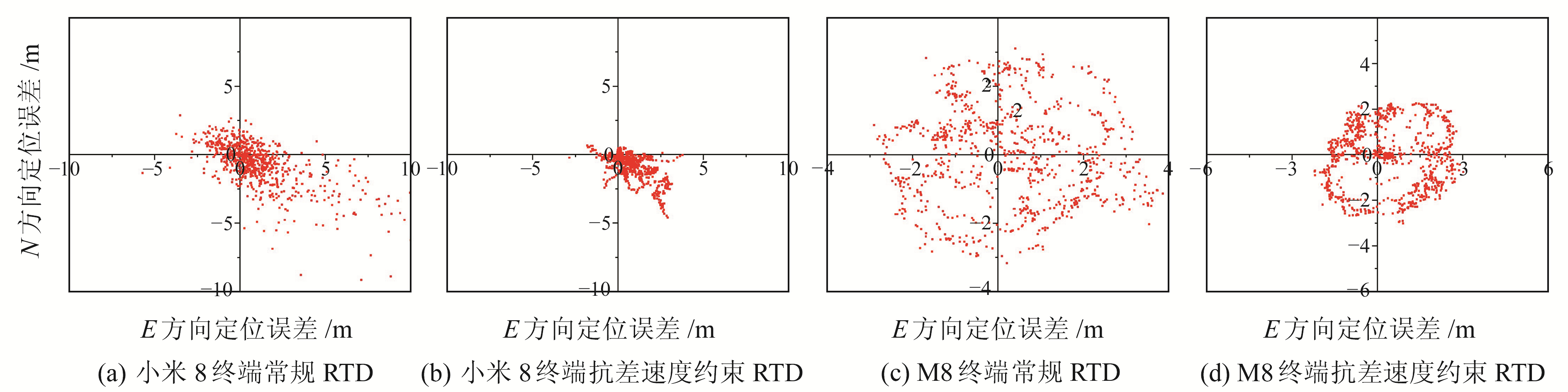
图 5给出了小米8和M8两种终端校园小路的RTD定位轨迹,定位轨迹中绿色点位为攀达专业接收机解算结果,黄色点位为常规RTD解算结果,红色点位为抗差速度约束RTD结果。图 6给出了小米8和M8两种终端在校园林荫小路RTD定位的平面误差。

|
图 5 智能移动终端校园小路RTD定位轨迹 Fig. 5 RTD positioning track of mobile intelligent terminal in campus path |
|
图 6 小米8终端和M8终端校园小路RTD平面定位误差 Fig. 6 RTD plane positioning errors of Mi 8 and M8 receivers in campus path |
由图 5可知,校园林荫小路动态实验中,小米8终端在遇到树木遮挡时“飞点”现象较为严重,整体轨迹并不明显;M8终端受遮挡影响较小,能形成稳定轨迹,在进行抗差速度约束后两种智能终端误差明显降低,且运动轨迹更为清晰,树木遮挡处“飞点”情况也得到极大控制。
由图 6可知,小米8终端的常规RTD有部分点误差较大,可达10 m,使用抗差速度约束RTD模型后严重的“飞点”大幅减少,东方向定位误差在2 m以内、北方向最大定位误差3 m左右;M8终端常规RTD平面方向定位误差大部分在5 m以内,使用抗差速度约束RTD模型后,东方向的大部分点位的定位精度可保证在3 m以内,北方向的大部分点位的定位精度可保证在2.5 m以内。
表 3(单位m)给出小米8和M8两种终端在动态模式下常规RTD和抗差速度约束RTD的RMS定位结果。由表可知,小米8终端的抗差速度约束RTD的平面误差RMS值为1.51 m,相较于常规RTD有1.20 m的精度提升;M8终端的抗差速度约束RTD的平面误差RMS值为1.49 m,相较于常规RTD有0.53 m的精度提升。
|
|
表 3 GNSS智能终端校园小路RTD RMS结果 Tab. 3 RTD RMS results of GNSS intelligent terminal in campus path |
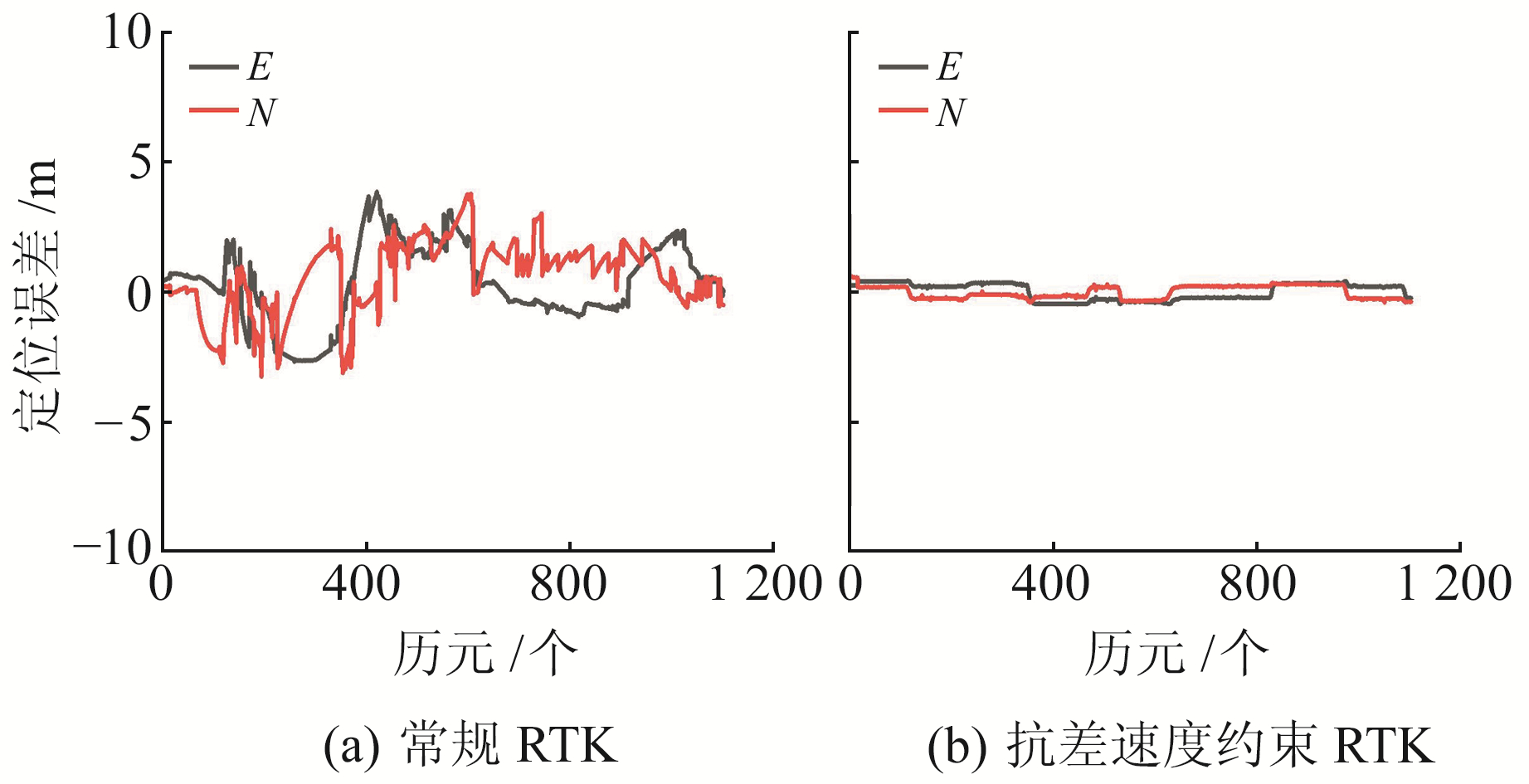
图 7给出了M8智能终端车载定位的轨迹图,图中绿色点位为专业接收机通过多系统多频段解算结果,均为固定解,将其作为参考点,红色点位为移动智能终端通过本文改进RTK定位解算结果,黄色点位为移动智能终端的常规RTK定位解算结果。图 8给出了M8终端在校园周边车载RTK定位在E、N方向的平面误差。

|
图 7 M8终端车载RTK定位轨迹路线 Fig. 7 Vehicle RTK positioning track route of M8 receiver |
|
图 8 M8车载E、N方向误差序列对比 Fig. 8 Comparison of M8 vehicle positioning errors between E and N direction |
由图 7可知,M8终端进行常规RTK解算时,在校园东侧道路遮挡区域出现比较明显的偏移,采用抗差速度约束RTK模型后,定位结果从全图轨迹上看并未出现明显偏差。除去常规RTK极少数较大的误差点,在图 7(b)、(c)放大图中可以看出,在开阔路段下M8智能终端2种RTK定位方案解算结果差别不大,但在遮挡处与转弯处抗差速度约束RTK结果明显更接近参考点位。
由图 8可知,常规RTK定位结果并不稳定,很多时段出现4 m左右的定位误差;而采用抗差速度约束RTK的定位结果相对常规RTK更为平稳,但在遮挡较为严重区域定位结果仍造成较大波动,抗差速度约束RTK在东、北方向的定位误差均在1 m以内。
表 4(单位m)给出M8终端在车载动态常规RTK和抗差速度约束RTK的RMS定位结果。可知,抗差速度约束RTK在东、北方向的误差分别为0.31 m和0.35 m,相对于常规RTK精度分别有1.22 m、1.35 m的提升;抗差速度约束RTK平面方向误差0.39 m,相对于常规RTK精度有1.89 m的提升;模糊度固定率提升29.4个百分点。
|
|
表 4 M8智能终端RTK RMS定位结果 Tab. 4 Positioning results of M8 intelligent terminal RTK RMS |
本文研究了一种附加多普勒原始观测值的抗差速度约束RTD模型和RTK自适应切换模型,通过对2种智能终端采集的数据分别进行静态实验和动态实验,结果表明:
1) 抗差速度约束RTD模型与RTK自适应切换模型相较于传统的RTD模型与RTK模型可有效提升定位精度,在部分遮挡动态实验中精度提升较为明显,体现了自适应切换的优势;M8终端在解算精度上优于小米移动终端,且在转弯处大大抑制了轨迹的偏移。
2) 静态RTD实验中,小米8终端抗差速度约束的RTD在东、北、高程方向的定位误差均在1.5 m以内,M8终端在东、北、高程方向的定位误差均在0.5 m左右,相较于常规RTD定位精度有明显提高。
3) 动态无遮挡/部分遮挡RTD实验中,小米8终端抗差速度约束的东方向定位精度提升1.03 m/0.60 m,北方向定位精度提升1.51m/1.06 m,平面定位精度提升1.8 m/1.20 m;M8终端抗差速度约束的东方向上定位精度提升0.39 m/0.47 m,北方向上定位精度提升0.38 m/0.49 m,平面定位精度提升0.77 m/0.53 m。
4) 车载动态RTK实验中,M8终端东、北、平面的定位误差均在0.5 m以内,东、北方向定位精度均提升超过1.2 m,平面定位精度提升约1.9 m,模糊度固定率提升近30个百分点,定位精度提升明显。
| [1] |
高成发, 陈波, 刘永胜. Android智能手机GNSS高精度实时动态定位[J]. 测绘学报, 2021, 50(1): 18-26 (Gao Chengfa, Chen Bo, Liu Yongsheng. Android Smartphone GNSS High-Precision Real-Time Dynamic Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(1): 18-26)
(  0) 0) |
| [2] |
郭斐, 吴维旺, 张小红, 等. Android智能手机实时精密单点定位软件实现及精度分析[J]. 武汉大学学报: 信息科学版, 2021, 46(7): 1053-1062 (Guo Fei, Wu Weiwang, Zhang Xiaohong, et al. Realization and Precision Analysis of Real-Time Precise Point Positioning with Android Smartphones[J]. Geomatics and Information Science of Wuhan University, 2021, 46(7): 1053-1062)
(  0) 0) |
| [3] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[J]. 测绘学报, 2020, 49(7): 938 (Zhou Feng. Theory and Methodology of Multi-GNSS Undifferenced and Uncombined Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(7): 938)
(  0) 0) |
| [4] |
刘万科, 史翔, 朱锋, 等. 谷歌Nexus9智能终端原始GNSS观测值的质量分析[J]. 武汉大学学报: 信息科学版, 2019, 44(12): 1749-1756 (Liu Wanke, Shi Xiang, Zhu Feng, et al. Quality Analysis of Raw GNSS Observation of Google Nexus 9 Smart Tablet Terminal[J]. Geomatics and Information Science of Wuhan University, 2019, 44(12): 1749-1756)
(  0) 0) |
| [5] |
Guo L, Wang F H, Sang J Z, et al. Characteristics Analysis of Raw Multi-GNSS Measurement from Xiaomi Mi 8 and Positioning Performance Improvement with L5/E5 Frequency in an Urban Environment[J]. Remote Sensing, 2020, 12(4): 744 DOI:10.3390/rs12040744
(  0) 0) |
| [6] |
Zhang K S, Jiao W H, Wang L, et al. Smart-RTK: Multi-GNSS Kinematic Positioning Approach on Android Smart Devices with Doppler-Smoothed-Code Filter and Constant Acceleration Model[J]. Advances in Space Research, 2019, 64(9): 1662-1674 DOI:10.1016/j.asr.2019.07.043
(  0) 0) |
| [7] |
Yong C Z, Odolinski R, Zaminpardaz S, et al. Instantaneous, Dual-Frequency, Multi-GNSS Precise RTK Positioning Using Google Pixel 4 and Samsung Galaxy S20 Smartphones for Zero and Short Baselines[J]. Sensors(Basel, Switzerland), 2021, 21(24): 8318 DOI:10.3390/s21248318
(  0) 0) |
| [8] |
Warnant R, Van De Vyvere L, Warnant Q. Positioning with Single and Dual Frequency Smartphones Running Android 7 or Later[C]. The 31st International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GNSS+ 2018), Miami, 2018
(  0) 0) |
| [9] |
Fortunato M, Critchley-Marrows J, Siutkowska M, et al. Enabling High Accuracy Dynamic Applications in Urban Environments Using PPP and RTK on Android Multi-Frequency and Multi-GNSS Smartphones[C]. 2019 European Navigation Conference(ENC), Warsaw, 2019
(  0) 0) |
| [10] |
王颖喆, 陶贤露, 朱锋, 等. 利用智能手机实现GNSS原始观测值的高精度差分定位[J]. 武汉大学学报: 信息科学版, 2021, 46(12): 1941-1950 (Wang Yingzhe, Tao Xianlu, Zhu Feng, et al. High Accuracy Differential Positioning with Smartphone GNSS Raw Measurements[J]. Geomatics and Information Science of Wuhan University, 2021, 46(12): 1941-1950)
(  0) 0) |
| [11] |
Wanninger L, Heelbarth A. GNSS Code and Carrier Phase Observations of a Huawei P30 Smartphone: Quality Assessment and Centimeter-Accurate Positioning[J]. GPS Solutions, 2020, 24(2)
(  0) 0) |
| [12] |
Geng J H, Li G C. On the Feasibility of Resolving Android GNSS Carrier-Phase Ambiguities[J]. Journal of Geodesy, 2019, 93(12): 2621-2635
(  0) 0) |
| [13] |
Zhang Q Q, Zhao L D, Zhao L, et al. An Improved Robust Adaptive Kalman Filter for GNSS Precise Point Positioning[J]. IEEE Sensors Journal, 2018, 18(10): 4176-4186
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44


