2. 63660部队,洛阳市,471000
2023-01-24 Galileo正式开始提供覆盖全球的免费HAS,这使得Galileo成为第一个在全球范围内提供此类高精度PPP服务的系统。在正式提供服务前,HAS进行了多阶段测试。Hauschild等[1]选择欧洲轨道中心的快速轨道和钟差产品分析HAS测试阶段的性能,结果表明,经HAS校正后的GPS和Galileo系统广播星历的空间信号测距误差(SISRE)分别为12~16 cm和7~9 cm。Fernandez-Hernandez等[2]分析HAS 2021-05的数据表明,Galileo和GPS的SISRE分别为9.5 cm和16 cm。Naciri等[3]在分析HAS改正的广播星历精度的基础上,测试HAS 2022年夏季的PPP定位性能,结果表明,其水平和垂直方向定位精度分别为13.1 cm和18.6 cm,满足该服务提出的预期指标,但HAS开通后的实际性能分析研究较少。本文主要针对HAS初始服务的性能表现,通过某高校校内架设的Septentrio接收机接收HAS改正数,分析其播发改正数的可用性、基于该服务的轨道钟差精度以及实际定位性能。
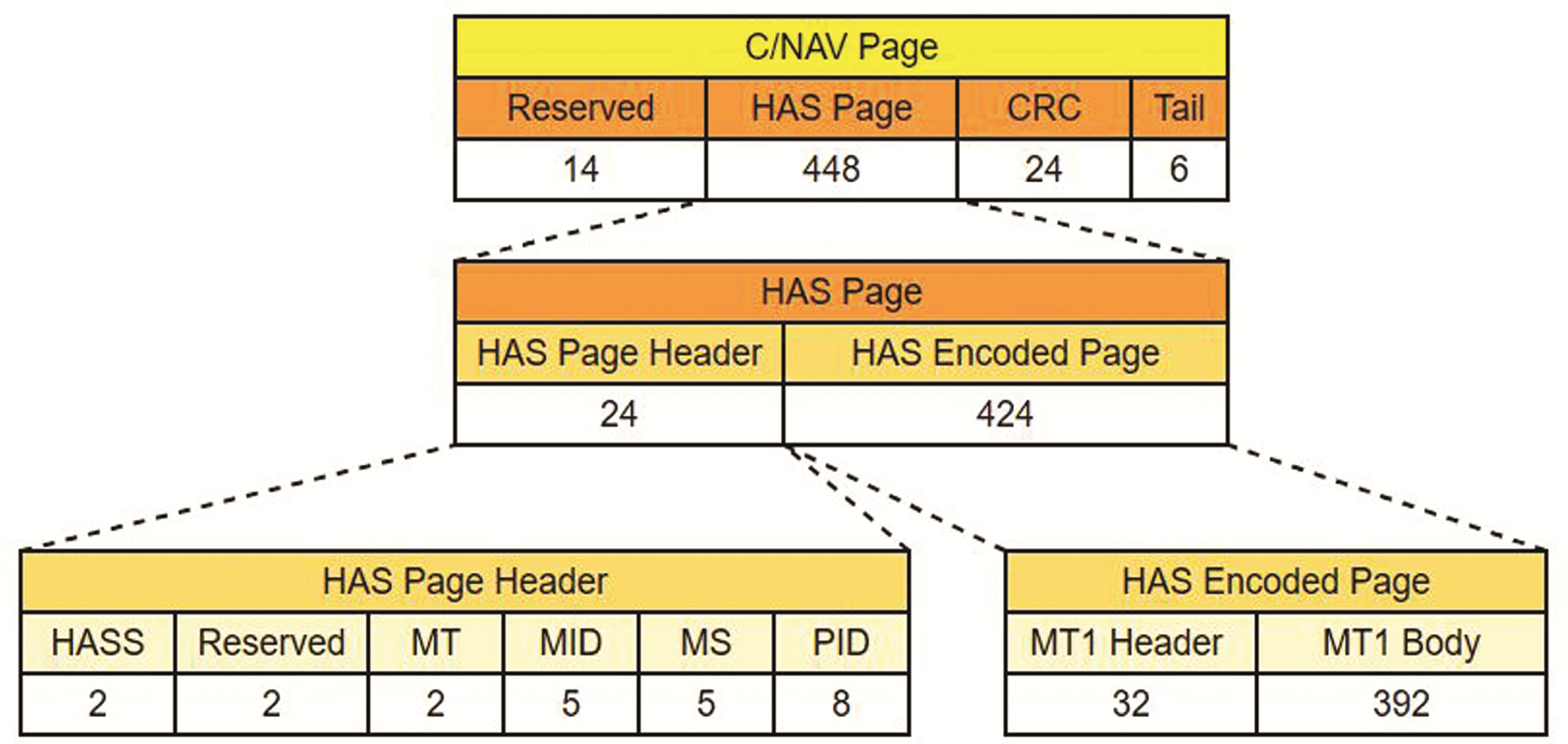
1 HAS服务改正信息结构Galileo卫星每秒通过E6B信号发送一个C/NAV页面,每个页面由492 bit组成,其中头部14位为预留位,末端由24位循环冗余校验码和6位尾部码组成,中间448位为HAS服务消息页面,每个消息页面由24位的消息头和424位的HAS服务解码页面组成。HAS解码页面由24位的报头和392位的消息数据构成,消息数据中包含掩码、轨道校正、钟差校正以及码偏差等改正数,具体结构如图 1所示。HAS用里德-所罗门编码将每条HAS信息编码成255个HAS消息页面,当用户接收到足够的消息页面时就可以对HAS消息进行解码。Oliver等[4]开发了用于将HAS服务改正信息转换为RTCM格式电文的工具HASlib,便于后续对HAS进行进一步分析。
|
图 1 HAS消息结构 Fig. 1 Message structure of HAS |
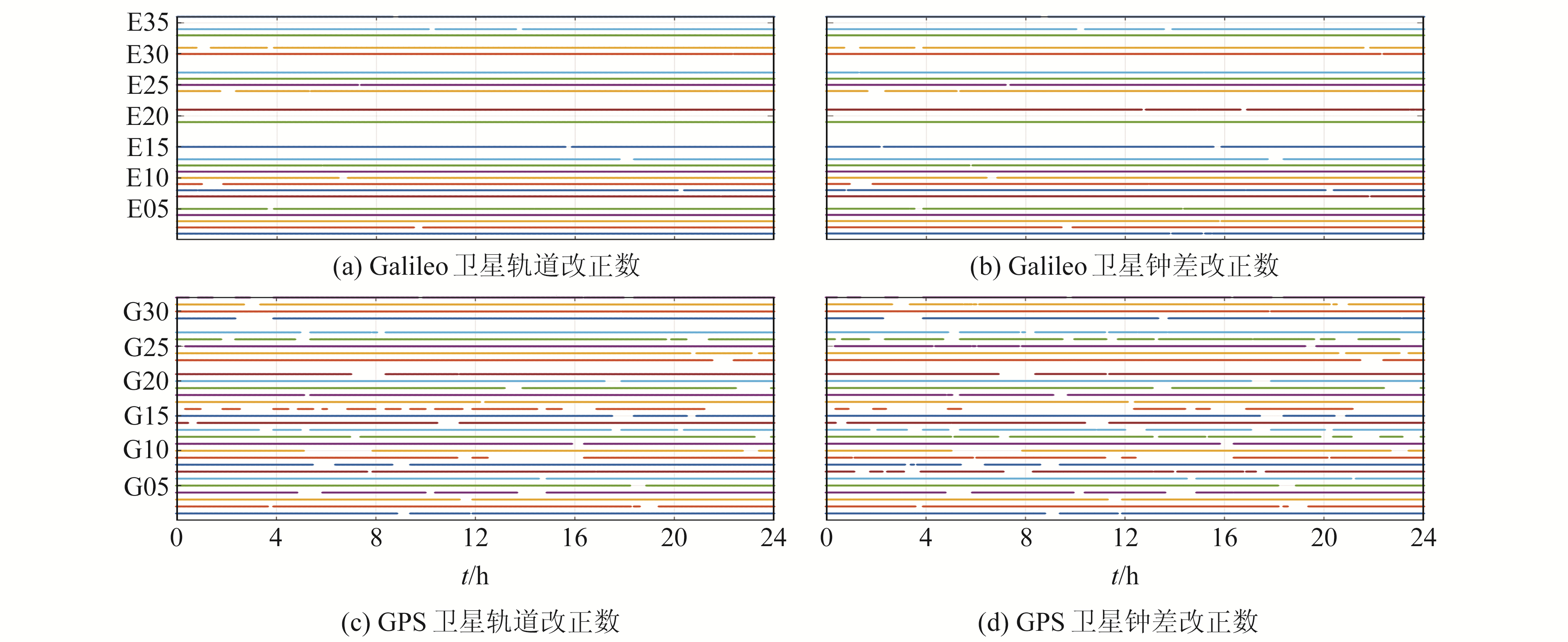
HAS目前在全球范围内播发Galileo和GPS系统轨道、钟差改正数以及伪距延迟,其改正信息包含的卫星可实现全球范围定位。HAS定义文档指出该服务为全球服务,其中60°N~60S°、90°E~125°W区域为排除地区,排除地区的用户仍然可以使用HAS,但可能无法达到设计的精度指标[5]。HAS全天播发改正数,轨道以及钟差分别以50 s和10 s的频率进行更新。为分析HAS改正数可用性,以2023-02-19全天HAS改正数接收情况为例,分析不同类型改正数的可用性,具体结果如图 2所示。
|
图 2 Galileo和GPS改正数接收情况 Fig. 2 Reception of Galileo and GPS corrections |
由图 2可见,目前HAS仍有部分卫星的改正数无法使用。相较于Galileo,GPS卫星的轨道和钟差改正数虽然也是全天可用,但是会在短时间内没有改正数且发生的频率较高。通过比较同一系统钟差和轨道改正数接收情况可以看出,轨道和钟差的可用情况大体一致。但是从G16卫星可以看出,因轨道和钟差的更新频率不一致,存在2个改正数可用时间不一致的情况,即在一定时间内可能只有一种改正数。整体上看,各卫星没有改正数的时间基本不重合,不会影响PPP的定位性能。为了更直观地展示可用性,各卫星改正数可用性统计结果如图 3。

|
图 3 各卫星的可用性 Fig. 3 Availability of each satellite |
由图 3可见,Galileo卫星基本90%以上的时间具有改正数,GPS卫星的可用性时间明显低于Galileo卫星。G16卫星轨道改正数仍有50%,但是没有相应时段的钟差改正数与其匹配,导致部分轨道改正数无效,因此G16卫星改正数的整体可用率约为34%,其余GPS系统卫星的改正数可用性都在75%以上。
3 HAS轨道钟差精度评估 3.1 HAS用户端改正算法HAS服务提供的轨道改正数是在卫星轨道坐标系下的向量,将其改正到对应时刻的广播星历需进行坐标转换,公式为:
| $ \left\{\begin{array}{l} \boldsymbol{e}_t=\frac{\dot{\boldsymbol{x}}^s}{\left|\dot{\boldsymbol{x}}^s\right|} \\ \boldsymbol{e}_w=\frac{\boldsymbol{x}^s \times \dot{\boldsymbol{x}}^s}{\left|\boldsymbol{x}^s \times \dot{\boldsymbol{x}}^s\right|} \\ \boldsymbol{e}_n=\boldsymbol{e}_t \times \boldsymbol{e}_w \\ \delta \boldsymbol{X}^s=\left[\begin{array}{lll} \boldsymbol{e}_n & \boldsymbol{e}_t & \boldsymbol{e}_w \end{array}\right] \delta \boldsymbol{O} \end{array}\right. $ | (1) |
式中,[en、et、ew]分别代表改正向量在径向、切向和法向3个方向上的单位向量;δX、δO分别为地心地固坐标系和卫星轨道坐标系下的改正向量。得到改正数后,将改正数中的星历龄期(issue of data, ephemeris, IODE)与广播星历中的IODE相匹配,可以得到改正后的卫星位置,具体公式为:
| $ \boldsymbol{X}_{\mathrm{HAS}}^s=\boldsymbol{X}_{\mathrm{brdc}}^s+\delta \boldsymbol{X}^s $ | (2) |
式中,Xbrdcs为通过广播星历计算得到的卫星位置,XHASs为改正后的卫星位置。
钟差改正数同样是作用于通过广播星历计算出的钟差之上,因此改正前需要匹配星历、轨道以及钟差的IODE,匹配成功后改正方式为:
| $ t_{\mathrm{HAS}}^s=t_{\mathrm{brdc}}^s+\frac{\partial C^s}{c} $ | (3) |
式中,tHASs、tbrdcs分别代表改正后的钟差和通过广播星历计算得到的钟差,δCs为钟差改正数,c为真空中光速。
3.2 改正数精度分析为评估基于HAS改正数的精度,现将经HAS改正的精密轨道钟差与武汉大学IGS数据中心提供的事后精密产品进行比较。由于事后精密产品提供的卫星位置是基于卫星的质心,而经HAS改正的卫星位置是基于卫星天线相位中心,因此需要考虑天线相位中心改正,将事后精密产品中的卫星位置改至天线相位中心,再同经HAS改正得到的卫星位置作差,并将差值转换到星固系下来分析HAS卫星轨道改正信息精度。
钟差方面,因基准不同,基于HAS的精密钟差与事后精密钟差产品间存在系统性偏差。为消除此偏差,需要对改正后的钟差进行二次作差后再进行分析[6],即先将改正后的钟差与同历元事后精密钟差产品作差得到一次差,将同一历元同一GNSS系统所有卫星的一次差取均值,再将各颗卫星的一次差与对应系统的一次差均值作差,得到二次差结果。具体公式为:
| $ \left\{\begin{array}{l} \Delta t^{i, s}=T^{i, s}-t^{i, s}-M \\ M=\frac{\sum\limits_{i=1}^n T^{i, s}-t^{i, s}}{n} \end{array}\right. $ | (4) |
式中,Ti, s、ti, s分别为某GNSS系统第i颗卫星的精密钟差以及改正后的钟差,M为该系统同一历元所有卫星一次差的均值。事后精密产品钟差的解算基准均为双频无电离层系统,GPS基准频率为C1W和C2W,Galileo基准频率为C1C和C5Q。而HAS中,GPS基准频率为C1C和C2P,Galileo基准频率为C1C和C7Q,因此要与事后产品进行精度比较仍需进行码偏差改正[3]。
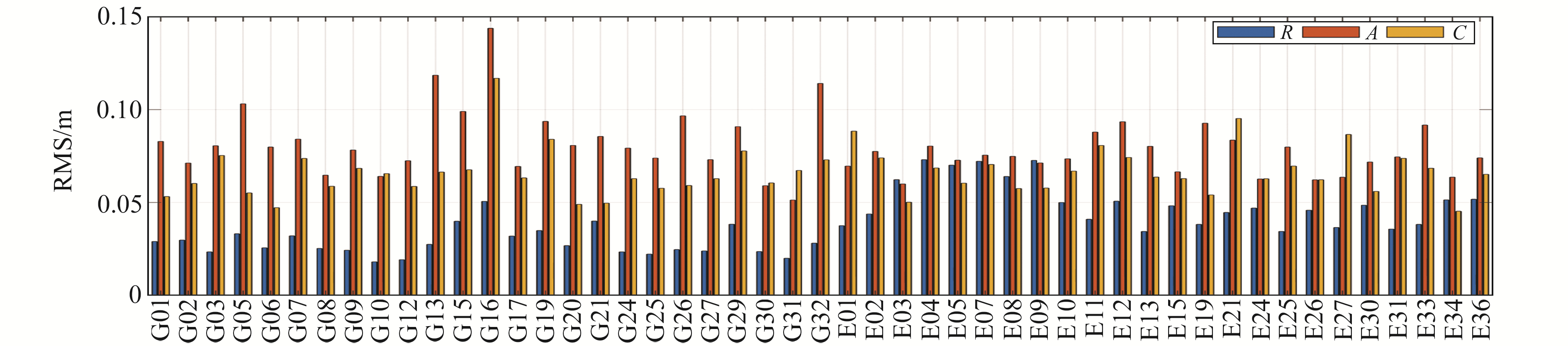
遵循以上处理方法,对2023-02-16~19基于HAS的精密钟差进行精度评估,结果如图 4、5所示。
|
图 4 HAS轨道产品精度 Fig. 4 The accuracy of HAS track product |

|
图 5 HAS钟差产品精度 Fig. 5 The accuracy of HAS clock correction product |
由图 4可见,在对定位精度影响最大的径向方向上,除了E03~E09这6颗卫星精度大于0.05m,其余卫星的精度均小于0.05m;在切向和法向上,大部分卫星的精度小于0.1 m。总体来看,在轨道精度方面,GPS略优于Galileo,且2个系统都拥有较高的轨道精度。
由图 5可见,所有卫星钟差的精度都在1 ns以内,并且Galileo卫星大部分的精度都在0.3 ns以下,明显优于GPS。
经HAS改正的精密轨道钟差与事后精密产品比较可以分析改正数质量,SISRE作为评估星历整体精度的综合指标,可以反映精密轨道钟差对用户定位性能的影响。SISRE有2种形式,分别为只考虑轨道误差贡献的形式和同时考虑轨道和钟差误差的形式[7],具体公式为:
| $ \left\{\begin{array}{l} \operatorname{SISRE}_{\text {orb }}=\sqrt{(\alpha \cdot \Delta R)^2+\beta\left(\Delta A^2+\Delta C^2\right)} \\ \text { SISRE }=\sqrt{(\alpha \cdot \Delta R-c \cdot T)^2+\beta\left(\Delta A^2+\Delta C^2\right)} \end{array}\right. $ | (5) |
式中,ΔR、ΔA、ΔC分别为2个产品轨道在径向、切向和法向上的误差;T为钟差;c为光速;α、β为权因子,其中,GPS的α、β分别取0.98、1/49,Galileo的α、β分别取0.98、1/61[8]。
按照式(5)对HAS进行SISRE分析,以武汉大学IGS数据中心提供的事后精密产品为参考基准,各系统轨道、钟差误差的RMS以及2种形式SISRE的RMS统计结果如表 1所示。
|
|
表 1 各系统产品精度以及SISRE结果 Tab. 1 Product accuracy and SISRE of each system |
由表 1可见,GPS径向上精度约为0.03 m,明显优于Galileo,在切向和法向上2个系统的精度相似。由式(5)可见,SISREorb主要受径向精度的影响,因此GPS的SISREorb明显优于Galileo。钟差方面,GPS的钟差精度约为0.53 ns,而Galileo系统的钟差仅约为0.28 ns。虽然GPS的SISREorb较优,但由于钟差精度差于Galileo,故GPS的SISRE为0.163 m,大于Galileo的0.097 m。
4 HAS定位精度分析为评估HAS实时PPP的性能,选取各个地区MGEX测站的观测数据,基于观测数据和采集的HAS轨道钟差改正数进行动态和静态PPP解算实验。因HAS官方发布的性能指标为水平方向0.2 m、垂直方向0.4 m,因此分别以0.2 m和0.4 m作为判定收敛时间的依据。具体定位解算策略如表 2所示。
|
|
表 2 PPP定位解算策略 Tab. 2 Solution strategy of PPP |
为测试HAS的定位精度,选取MGEX全球范围内10个测站2023-02-17~23的观测数据进行定位精度分析,测站坐标如表 3所示,其中GAMG、MIZU和HOLB测站不在HAS范围内。
|
|
表 3 测站坐标 Tab. 3 Station coordinates |
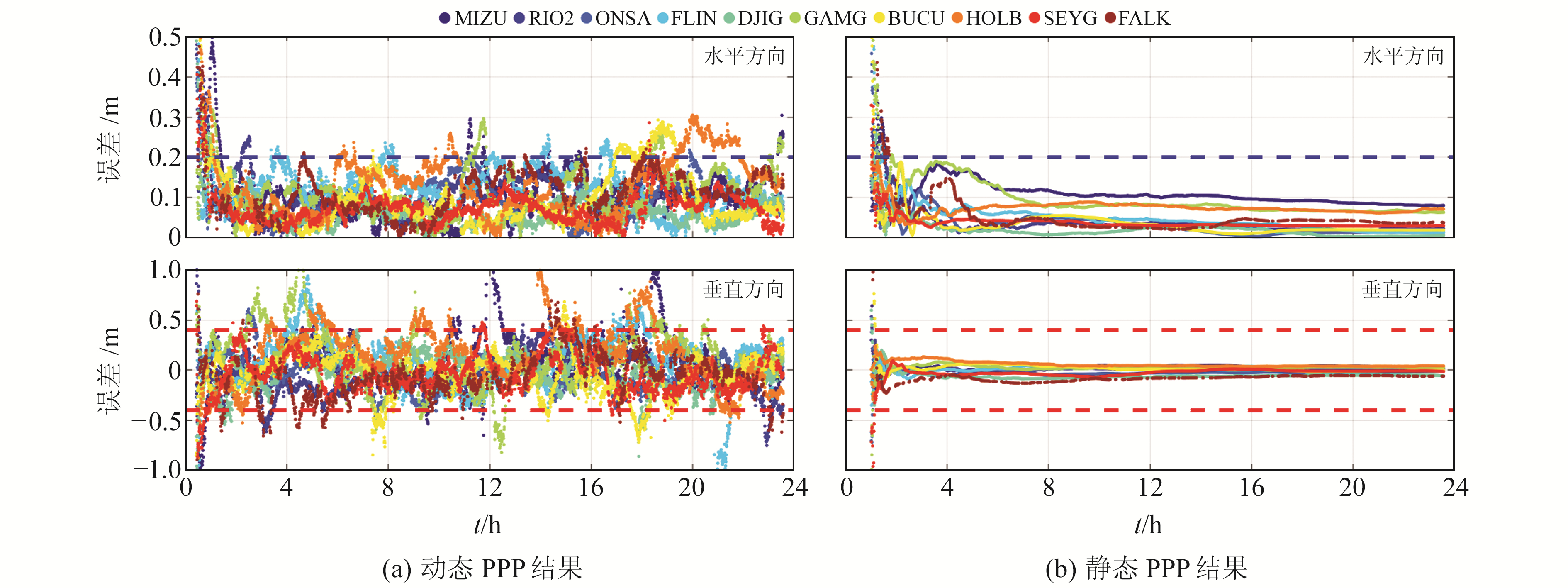
图 6为10个测站02-18定位结果,图中虚线分别代表水平方向的0.2 m和垂直方向的0.4 m的性能指标,收敛定义为满足定位精度且持续至少5 min。图 6(a)为动态PPP结果,可以看出,在水平方向的收敛速度上,不在HAS范围的MIZU、GAMG、HOLB测站收敛略慢于其他测站;在定位精度方面,BUCU、HOLB、MIZU、GAMG、FLIN测站出现定位序列波动超出0.2 m的情况,但10个测站整体的定位序列都在0.2 m以下。垂直方向上,各个测站的收敛速度快于水平方向,但多个测站的定位误差多次出现超出0.4 m的情况,其中GAMG、MIZU、HOLB、FLIN测站的波动较为明显,最大达到1 m左右,但垂直方向的整体定位精度仍在0.4 m以内。图 6(b)为静态PPP结果,可以看出,水平方向MIZU、FALK测站收敛较慢,各个测站收敛后的定位精度均在0.1 m以内;垂直方向上各个测站均能较快收敛,且定位精度较为接近。
|
图 6 HAS PPP性能 Fig. 6 The PPP performance of HAS |
为更好地测试HAS PPP的性能,基于上述10个测站02-17~23的观测数据进行PPP实验,定位序列误差的RMS统计值如表 4所示。
|
|
表 4 PPP结果 Tab. 4 The results of PPP |
表 4中的2行均值分别代表HAS范围内(均值1)以及范围外(均值2)测站定位精度的均值。可以看出,定位精度方面,静态PPP时10个测站水平和垂直方向上的定位精度都优于10 cm,且HAS范围内外的测站定位效果接近;动态PPP时,服务范围外测站在水平和垂直方向上的定位精度明显较差,但结果仍满足服务性能指标。收敛速度方面,垂直方向上的收敛速度优于水平方向,且静态PPP的收敛速度明显快于动态PPP,10个测站除了静态PPP垂直方向上基本能够满足收敛时间小于5 min的指标,其他情况下与HAS所提指标仍存在一定的差距,特别是GAMG、MIZU测站收敛效果较差。
5 结语1) 在服务可用性方面,HAS可在全球范围内播发改正数,Galileo的卫星改正数可用性大于90%,GPS的卫星改正数可用性明显低于Galileo,部分卫星改正数可用性低于80%。
2) 在产品精度方面,GPS在径向、切向、法向上的精度分别为0.029 m、0.086 m、0.066 m,Galileo的精度分别为0.051 m、0.076 m、0.068 m;GPS和Galileo的钟差RMS分别为0.533 ns和0.281 ns。虽然GPS的轨道精度优于Galileo,但Galileo整体的空间信号精度更高,SISRE值为0.097 m,优于GPS系统的0.163 m。
3) 在定位精度方面,选取的测站在动态和静态PPP条件下均可以达到HAS指标所提的水平方向小于0.2 m、垂直方向小于0.4 m。在HAS范围外的测站同样可以接收改正数进行PPP定位,定位精度稍差于服务范围内的测站,但仍然满足服务标准。
4) 在收敛速度方面,静态和动态PPP时,垂直方向上的收敛速度明显快于水平方向,且静态PPP明显优于动态PPP,但是仅部分测站静态PPP垂直方向上的收敛速度能够小于300 s,其余无法达到300 s的收敛标准,且服务范围外的测站收敛效果更差。
| [1] |
Hauschild A, Montenbruck O, Steigenberger P, et al. Orbit Determination of Sentinel-6A Using the Galileo High Accuracy Service Test Signal[J]. GPS Solutions, 2022, 26(4)
(  0) 0) |
| [2] |
Fernandez-Hernandez I, Chamorro-Moreno A, Cancela-Diaz S, et al. Galileo High Accuracy Service: Initial Definition and Performance[J]. GPS Solutions, 2022, 26(3)
(  0) 0) |
| [3] |
Naciri N, Yi D, Bisnath S, et al. Assessment of Galileo High Accuracy Service(HAS) Test Signals and Preliminary Positioning Performance[J]. GPS Solutions, 2023, 27(2)
(  0) 0) |
| [4] |
Horst O, Kirkko-Jaakkola M, Malkamäki T, et al. HASlib: An Open-Source Decoder for the Galileo High Accuracy Service[C]. 35th International Technical Meeting of the Satellite Division of the Institute of Navigation, Denver, 2022
(  0) 0) |
| [5] |
European Union. Galileo High Accuracy Service Service Definition Document(HAS SDD), Issue1.0[EB/OL]. https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo-HAS-SDD_v1.0.pdf, 2023-01-24
(  0) 0) |
| [6] |
Montenbruck O, Steigenberger P, Hauschild A. Broadcast Versus Precise Ephemerides: A Multi-GNSS Perspective[J]. GPS Solutions, 2015, 19(2): 321-333 DOI:10.1007/s10291-014-0390-8
(  0) 0) |
| [7] |
Heng L, Gao G X, Walter T, et al. Statistical Characterization of GPS Signal-in-Space Errors[C]. 2011 International Technical Meeting of the Institute of Navigation, San Diego, 2011
(  0) 0) |
| [8] |
中国卫星导航系统管理办公室测试评估研究中心. 北斗服务性能[EB/OL]. http://www.csno-tarc.cn/performance/sisre, 2023-03-10 (Test and Assessment Research Center of China Satellite Navigation Office. Beidou Service Performance[EB/OL]. http://www.csno-tarc.cn/performance/sisre, 2023-03-10))
(  0) 0) |
2. 63660 Troops of PLA, Luoyang 471000, China
 2024, Vol. 44
2024, Vol. 44

