随着全球导航卫星系统GNSS的快速发展，许多国家和组织在全球建立了大量GNSS观测站^[1]，GNSS观测站的长时间坐标时间序列可为板块运动、地震以及速度场、形变场等地球动力学研究提供准确数据。由于观测站在观测过程中会出现各种不确定因素，使得时间序列出现数据缺失^[2]，因此需要对缺失的时间序列进行修复。

目前比较常见的插值方法有拉格朗日法、三次样条法和正交多项式法^[3]：武艳强等^[4]基于三次样条插值法提出多点三次样条法，此方法能够在连续缺失数据时提高插值精度；Dong等^[5]基于坐标序列的缺失情况，使用不同的插值方法，采用周围站点的坐标平均值作内插处理；田慧等^[6]采用二阶正交多项式拟合最小二乘曲线法进行插值，能够较好地反映原始时序的运动趋势。但上述方法大多基于数学模型^[7]，没有考虑到实际的变化因素。近年来，国内外许多学者提出了更符合实际的方法：Carrizosa^[8]使用优化后的变邻域搜索算法(variable neighborhood search, VNS)对时间序列缺失值进行修复，保留了原始数据的统计学特性；王方超等^[9]将调整最大似然法(regularized EM algorithm, RegEM)引入到GNSS时间序列插值中，该方法不依靠数学模型和先验信息，而是依赖数据特性进行插值。

通过同步观测卫星的方式在GNSS卫星定位中选取任意2个测站，可以得到其三维坐标和一条基线向量，通过建立基线向量网对待求测站的坐标进行平差计算。考虑到待求点与周围测站具有相同的变化趋势，联合待求点及其周围区域已知测站构建GNSS网进行拟稳平差计算，得到待求点坐标，并与拉格朗日法和三次样条法进行对比，验证其可行性。

1 基本原理和精度评定指标 1.1 拟稳平差法基本原理

由于存在各种误差，测量过程中数据可能有一定程度的波动，会对平差结果产生影响。本文提出一种基于间接平差法，根据相对稳定的测站坐标时间序列变化预测待求点坐标变化的时间序列分析方法。其平差准则为：

$ \left\{\begin{array}{l} \boldsymbol{V}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{V}=\min \\ \boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}=\min \end{array}\right. $

(1)

式中，V为观测误差，P为权向量，X为平差网中拟稳点的未知参数。

在公共历元数据中选出与待求点总体运动趋势相近的测站(即拟稳点)，将上述测站作为基准站，以基准站第n天的三维坐标和待求点的近似三维坐标作为初始值，设待求点第(n+1)天的坐标为参数，可以表示为：

$ \left[\begin{array}{c} \hat{X}_{i} \\ \hat{Y}_{i} \\ \hat{Z}_{i} \end{array}\right]=\left[\begin{array}{c} X_{i}^{0} \\ Y_{i}^{0} \\ Z_{i}^{0} \end{array}\right]+\left[\begin{array}{c} \hat{x}_{i} \\ \hat{y}_{i} \\ \hat{z}_{i} \end{array}\right], \left[\begin{array}{c} \hat{X}_{j} \\ \hat{Y}_{j} \\ \hat{Z}_{j} \end{array}\right]=\left[\begin{array}{c} X_{j}^{0} \\ Y_{j}^{0} \\ Z_{j}^{0} \end{array}\right]+\left[\begin{array}{c} \hat{x}_{j} \\ \hat{y}_{j} \\ \hat{z}_{j} \end{array}\right] $

(2)

式中，$\left(\hat{X}_{i}, \hat{Y}_{i}, \hat{Z}_{i}\right)$为待求点第(n+1)天的坐标，(X_i⁰, Y_i⁰, Z_i⁰)为待求点第n天的坐标，$\left(\hat{x}_{i}, \hat{y}_{i}\right.$, $\left.\hat{z}_{i}\right)$为待求点平差值，$\left(\hat{X}_{j}, \hat{Y}_{j}, \hat{Z}_{j}\right)$为基准站第(n+1)天的坐标，(X_j⁰, Y_j⁰, Z_j⁰)为基准站第n天的坐标。2个测站可以构建出一条基线向量，其三维坐标差值为：

$ \left[\begin{array}{l} \Delta \hat{X}_{i j} \\ \Delta \hat{Y}_{i j} \\ \Delta \hat{Z}_{i j} \end{array}\right]=\left[\begin{array}{c} \hat{X}_{j} \\ \hat{Y}_{j} \\ \hat{Z}_{j} \end{array}\right]-\left[\begin{array}{c} \hat{X}_{i} \\ \hat{Y}_{i} \\ \hat{Z}_{i} \end{array}\right]=\left[\begin{array}{l} \Delta X_{i j}+V_{X_{i j}} \\ \Delta Y_{i j}+V_{Y_{i j}} \\ \Delta Z_{i j}+V_{Z_{i j}} \end{array}\right] $

(3)

得到基线的误差方程为：

$ \underset{3 n \times 1}{\boldsymbol{V}}=\underset{3 \times 1}{\hat{\boldsymbol{x}}_j}-\underset{3 \times 1}{\hat{\boldsymbol{x}}}-\underset{3 \times 1}{\boldsymbol{l}_K} $

(4)

式中，$\underset{\boldsymbol{K} \times 1}{\boldsymbol{l}}=\Delta \underset{3 \times 1}{\hat{\boldsymbol{x}}}-\Delta \underset{3 \times 1}{\boldsymbol{x}_{i, j}}$。

当GNSS观测网中有m个待求点、n条基线向量时，GNSS基线网的误差方程为：

$ \underset{3 n \times 1}{\boldsymbol{V}}=\underset{3 n \times 3 n}{\boldsymbol{B}}\; \underset{3 m n \times 1}{\hat{\boldsymbol{x}}}-\underset{3 n \times 1}{\boldsymbol{l}} $

(5)

式中，$\underset{3 n \times 3 n}{\boldsymbol{B}}$为基线观测方程阵，$\underset{3 n \times 1}{\boldsymbol{l}}$为GNSS网内所有测站第(n+1)天的三维坐标与第n天的三维坐标差值之间的差。为方便计算，令先验单位权中误差σ₀=0.001，其权阵为：

$ \boldsymbol{P}=\left(\boldsymbol{D} / \sigma_{0}^{2}\right)^{-1} $

(6)

式中，D为基线向量协方差阵。令N_BB=B^TPB, W=B^TPl，使用间接平差法组建法方程：

$ \boldsymbol{N}_{B B} \hat{\boldsymbol{x}}=\boldsymbol{W} $

(7)

求出法方程的解$\hat{\boldsymbol{x}}$，从而得到待求点第(n+1)天的三维坐标。对平差后的三维坐标结果进行精度评定：

$ \begin{aligned} & \hat{\sigma}_{0}=\sqrt{\frac{\boldsymbol{V}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{V}}{n-t}}, \sigma_{\hat{x}_{i}}=\hat{\sigma}_{0} \sqrt{\boldsymbol{Q}_{\hat{x}_{i} \hat{x}_{i}}}, \\ & \sigma_{\hat{y}_{i}}=\hat{\sigma}_{0} \sqrt{\boldsymbol{Q}_{\hat{y}_{i} \hat{y}_{i}}}, \sigma_{\hat{z}_{i}}=\hat{\sigma}_{0} \sqrt{\boldsymbol{Q}_{\hat{z}_{i} \hat{z}_{i}}} \end{aligned} $

(8)

式中，Q为N_BB的逆矩阵。

1.2 精度指标

通过人为打断时间序列的方式模拟缺失的时间序列，并使用平均绝对误差MAE、均方根误差RMSE以及Pearson相关系数3种指标对插值结果进行分析。MAE与RMSE用来衡量插值与实际观测值之间的偏差，MAE为L1范数，RMSE为L2范数，次数越高对于异常值越敏感。Pearson相关系数用来衡量2个数据间的相关程度，系数取值为-1~1。

平均绝对误差MAE的计算公式为：

$ \mathrm{MAE}=\frac{1}{n} \sum\limits_{m=1}^{n}\left(p_{m}-o_{m}\right) $

(9)

均方根误差RMSE的计算公式为：

$ \operatorname{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{m=1}^{n}\left(p_{m}-o_{m}\right)^{2}} $

(10)

Pearson相关系数的计算公式为：

$ \gamma_{\mathrm{P}}=\frac{1}{n-1} \sum\limits_{m}^{n}\left(\frac{p_{m}-\bar{p}}{\sigma_{p}}\right)\left(\frac{o_{m}-\bar{o}}{\sigma_{o}}\right) $

(11)

式中，p_m、o_m为第m个插补值和真实值，$\bar{p}、\bar{o} $、σ_p、σ_o分别为插补值和真实值的平均值与标准差。RMSE和MAE越小，说明插值结果与实际观测值越接近；Pearson相关系数的绝对值越接近1，说明插值后的时间序列与原始时间序列的相关性越高。

2 模拟数据实验分析

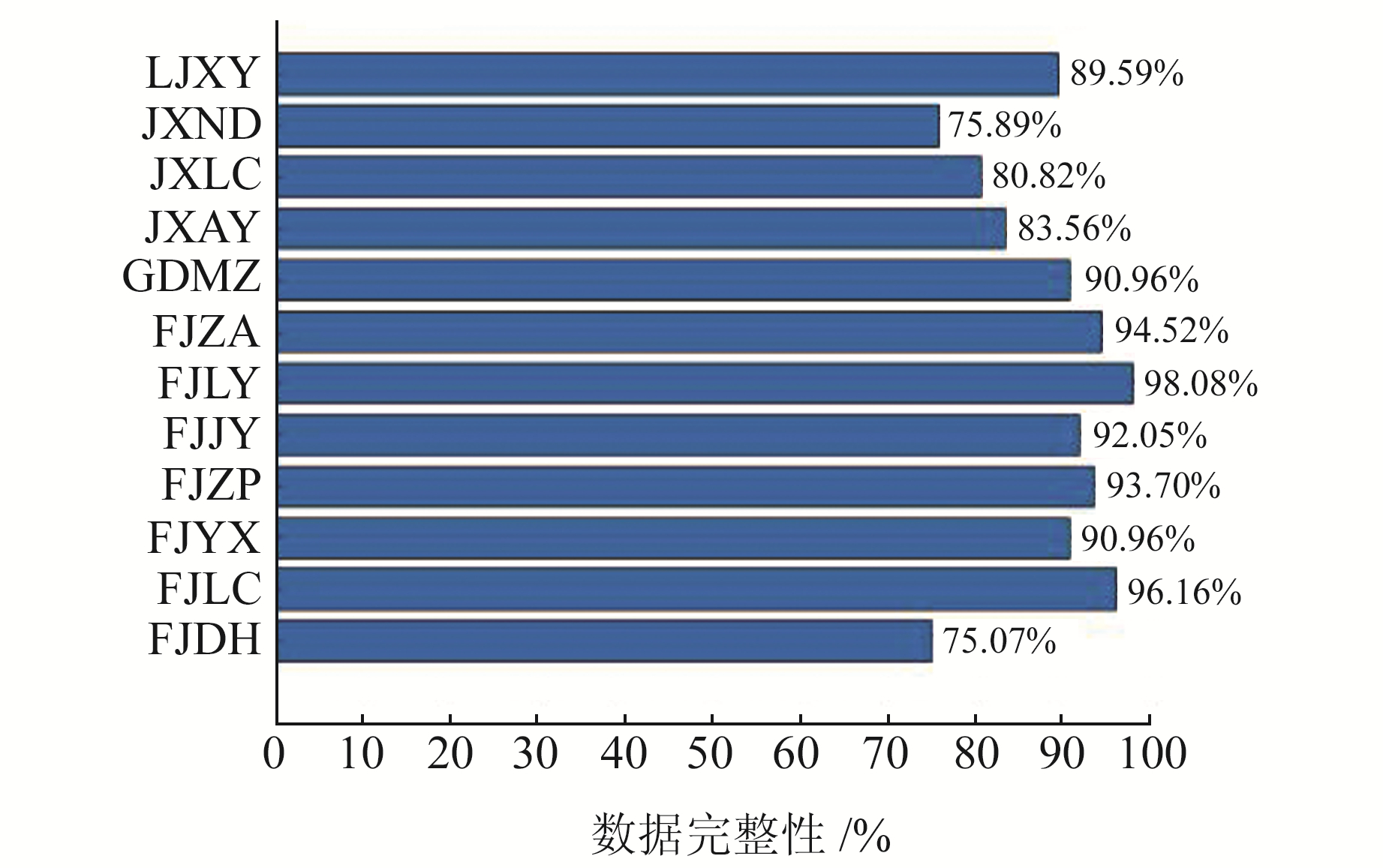
为体现插值方法的客观性，采用中国地壳运动观测网络的真实数据进行模拟实验。选择我国东南沿海地区的FJDH、FJYX、FJZP、FJLC四个测站为研究对象，与周围相关性较强的测站组成GNSS相对观测网。测区内各测站2021年的数据完整情况如图 1所示。

由图 1可见，各测站在2021年的观测数据完整率均在70%以上，大部分测站数据缺失率约为10%，可以保证每个历元至少有一半以上的测站用于组建GNSS网进行平差计算。

为模拟缺失数据，将2021年剔除粗差后的FJDH、FJYX、FJZP、FJLC观测站的时间序列人为打断成5 d、30 d、90 d的数据。其中FJDH站删除doy16~20、doy31~60、doy91~180的数据，FJYX站删除doy16~20、doy31~60、doy71~160的数据，FJZP站删除doy91~180、doy251~255、doy301~330的数据，FJLC站删除doy31~35、doy91~120、doy151~240的数据。分别使用拉格朗日法、三次样条法、拟稳平差法进行插值处理，基于一致性和随机性进行对比分析。在使用拉格朗日法与三次样条法时，根据缺失天数选择缺失数据前后相同区域的数据，平均分成3份后选出6~8 d的数据作为样本构建函数进行插值。采取拟稳平差法计算时，使用含有待求点缺失序列的测站进行计算，可以分段进行插值。由于篇幅有限，模拟实验仅在高程方向进行。原始时间序列与3种插值方法的结果如图 2所示。

由图 2可见，在缺失5 d数据的情况下，拉格朗日法、三次样条法和拟稳平差法的插值结果与原始序列之间不存在偏移，表现稳定；在缺失30 d数据的情况下，拉格朗日法和三次样条法无法反映原始序列的趋势，会产生凸起并存在较大偏移，而拟稳平差法的插值结果与原始序列一致；在缺失90 d数据的情况下，3种方法的插值结果与缺失30 d数据的结果相似，但拟稳平差法的一致性更明显。由此可见，拟稳平差法的优势在于能够利用周围测站的信息估算待求点的运动状态，从而减小数据缺失对插值结果的影响。而基于多项式的线性插值方法只能保证时间序列的连续性和光滑性，无法保证与原始序列的关联性。因此在数据缺失较多时，可以使用拟稳平差法进行插值修复。

为了更直观地体现3种插值方法的效果，将插值部分进行放大处理，如图 3所示。在数据缺失较少的情况下，3种方法的插值结果与原始数据之间的误差较小，其中拉格朗日法与三次样条法的结果基本一致。在缺失30 d、90 d数据的情况下，拉格朗日法与三次样条法的插值结果与原始序列偏差较大，最高达23 mm和17 mm，而拟稳平差法单日最大误差为13 mm，说明拟稳平差法的一致性更好。

表 1(单位mm)为3种插值方法的精度指标。从插值方法的精度看，在缺失5 d数据的情况下，3种方法的MAE与RMSE差距不大，说明3种方法在缺失少量数据时插值效果相当；在缺失大量数据的情况下，3种方法的修复效果存在显著差异，拟稳平差法的MAE与RMSE指标误差最小，在6 mm以内，相比其他2种方法精度分别提高10%和60%。从相关系数来看，在缺失5 d数据的情况下，3种方法在原始序列波动较大的FJLC、FJZP站的相关系数较小，拉格朗日法与三次样条法在时间序列较为平缓的FJDH、FJYX站的相关性略高于拟稳平差法；在缺失30 d和90 d数据的情况下，拟稳平差法的相关系数要远远大于其他2种插值方法，说明拟稳平差法与原始序列的运动趋势具有较高的相似性。

3 拟稳平差算法仿真实验

首先使用拟稳平差法补齐测区内2021年测站的时间序列，得到完整的时间序列；然后选择FJZP站作为待求点，使用拟稳平差法对补齐后的观测站进行仿真实验；最后将仿真值与真实值进行比较，评估拟稳平差法在时间序列仿真中的可信度。

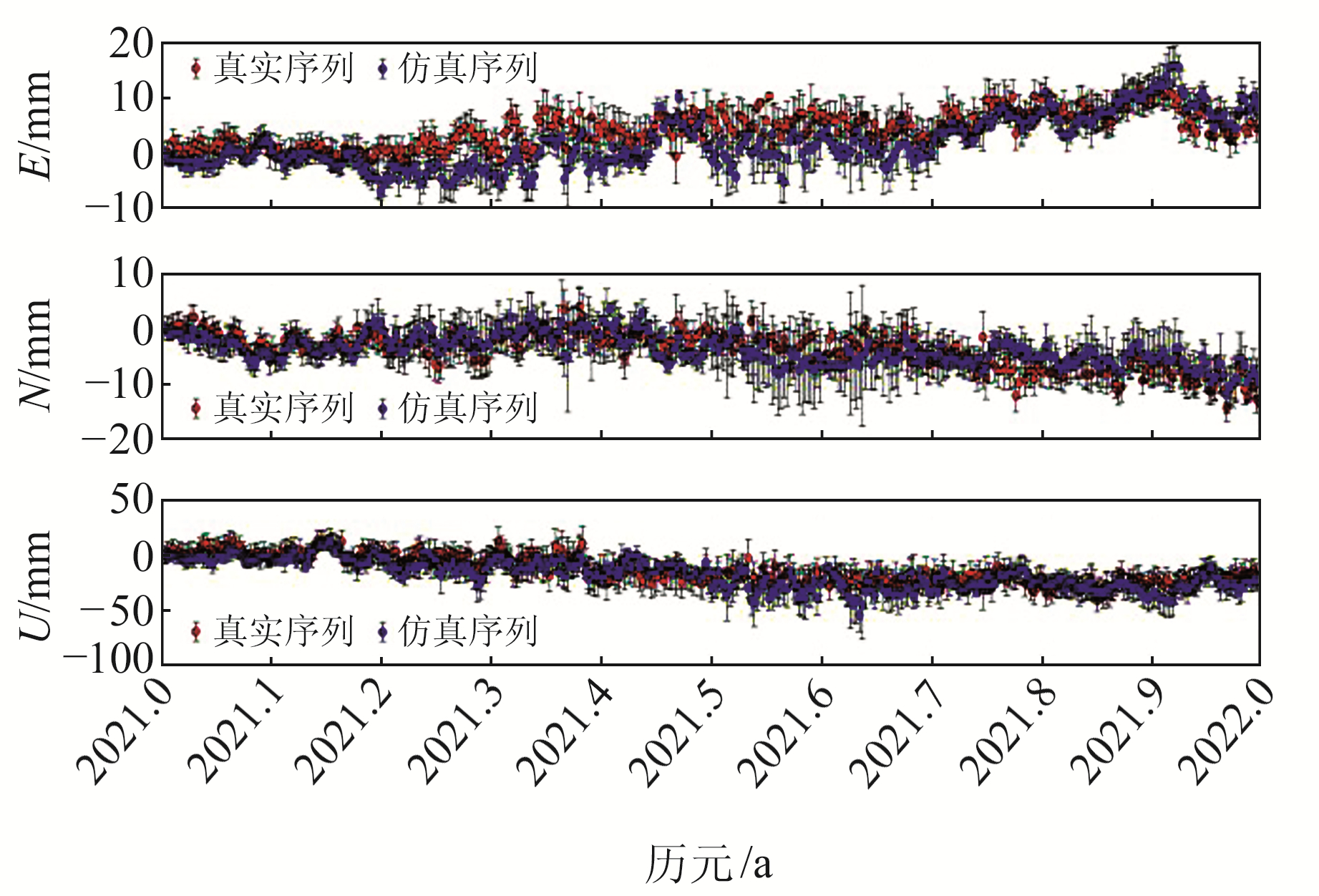
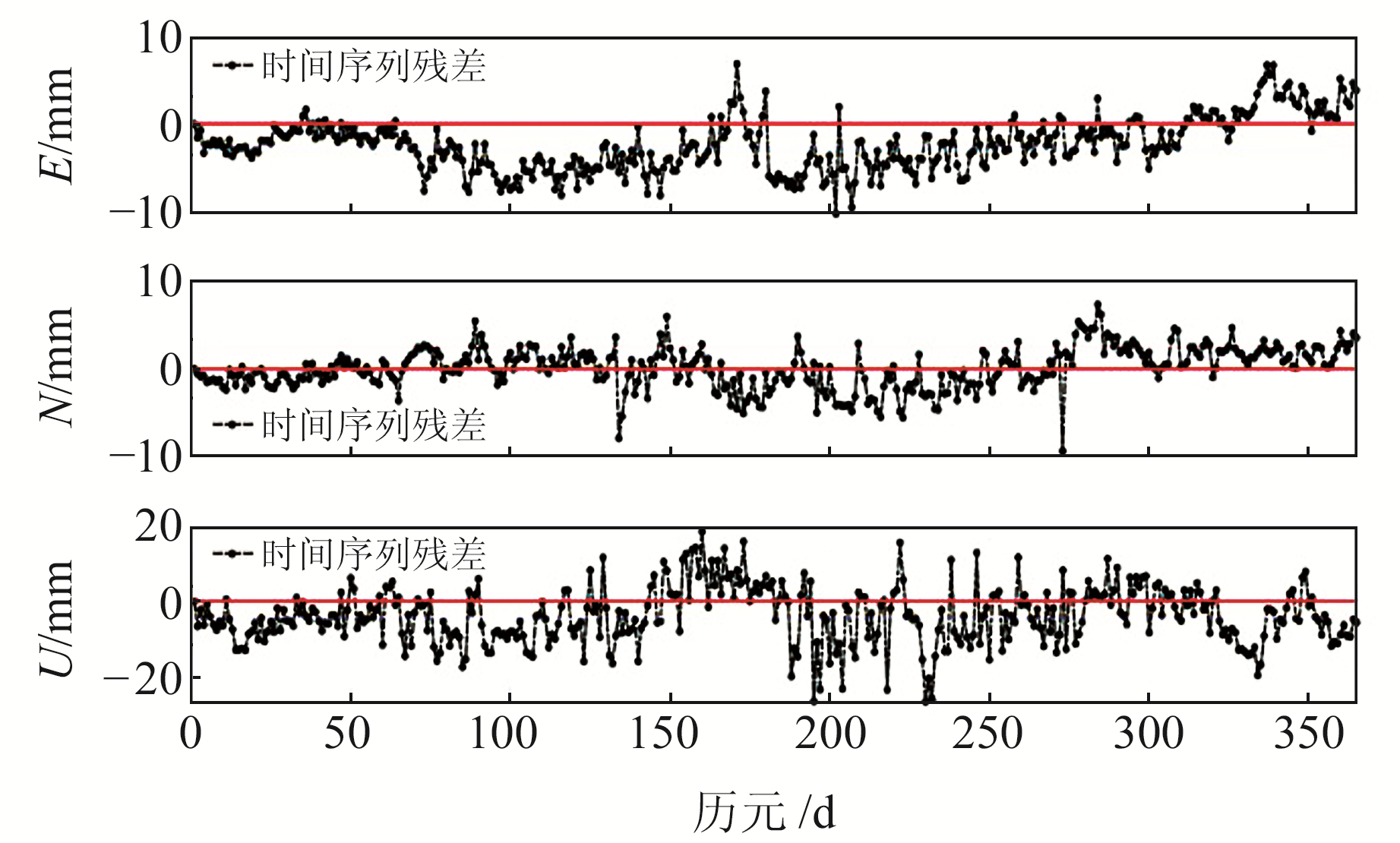
由图 4可知，通过拟稳平差法仿真出的序列与真实序列基本重叠，且3个方向上的运动趋势基本一致。将每个历元的仿真值与真实值作差得到FJZP站2021年的时间序列残差，如图 5所示。由图可见，3个方向上仿真值与真实值的残差均在0 mm附近波动，E、N方向上的时间序列残差在10 mm以内，U方向上的时间序列残差在20 mm以内。

由表 2(单位mm)可见，N方向上的误差最小，约为2 mm；E方向次之，误差约为3.5 mm；U方向误差最大，约为7~8 mm。3个方向上的皮尔逊相关系数达0.7~0.8，表明仿真值与真实值之间的相关性较高。从出现异常值的情况看，3个方向上的RMSE与MAE相差不大，说明出现异常值的概率非常小。由此可知，通过拟稳平差法得到的仿真数据与真实数据基本同步，在精度上能满足测量要求，可以用作更进一步的研究。

4 结语

1) 当数据缺失较少时，3种方法的插值结果都很理想，与真实值的偏差较小，且对于较为平稳的时间序列，拉格朗日法和三次样条法与真实值的相关性更高；在缺失30 d和90 d数据的情况下，拉格朗日法与三次样条法出现凸起，与真实值出现较大幅度的偏移，而拟稳平差法可以根据周围测站的运动趋势较好地插值出待求点的时间序列。

2) 使用拟稳平差法得到待求点完整的时间序列，计算得到仿真值与真实值的残差，E和N方向上的残差约为3 mm，U方向上的残差约为7~8 mm，且仿真值与真实值的相关性较高。

拟稳平差法在时间序列空缺插值中具有较高的准确性和可靠性，能够有效补齐缺失数据，并能在一定程度上模拟真实观测值，提供高精度的数据基础。