2. 武汉大学卫星导航定位技术研究中心,武汉市珞喻路129号,430079
随着全球卫星导航系统(global navigation satellite system,GNSS)观测技术的不断发展、数据分析工具的不断完善以及地面基准站数量的不断增多,GNSS大地测量技术的定位精度和稳定性得到前所未有的提高,使其成为地壳形变和地球板块运动监测的重要技术之一。区域GNSS网因受地壳运动、地表质量负载、数据处理策略等因素的影响,坐标时间序列中通常存在局部的时空相关性误差,即共模误差(common mode error,CME),共模误差的有效提取对GNSS地学研究具有重要意义[1-2]。共模误差提取方法包括堆栈法、主成分分析法和Karhunen-Loeve展开法。大量研究表明,在数百千米范围的区域GNSS网中,3种方法均能有效提取共模误差,但堆栈法假设共模误差在空间上均匀分布,若站点分布不均匀或范围过大,共模误差会减弱甚至消失,而主成分分析法不但在小范围GNSS网中表现更佳,同时适用于大尺度、大范围、非均匀分布的GNSS网共模误差提取[3-7]。
贵州为典型喀斯特地形地貌地区,地质构造复杂脆弱,容易引发滑坡、崩塌、泥石流等地质灾害,已经成为我国地质灾害最严重的省份之一。利用长期连续观测的GNSS基准站数据监测喀斯特地貌地区地形变发育过程,对研究喀斯特地质形变规律具有一定的参考意义。本文利用贵州省北斗卫星导航定位基准站网(GZCORS)GNSS观测数据,采用主成分分析法提取站坐标共模误差,采用最大似然估计法确定各测站不同坐标分量的最佳噪声模型,并估计最佳噪声模型的站点年变化率。
1 数据处理 1.1 GNSS站点坐标解算为研究贵州喀斯特地貌地区GNSS站坐标时间序列噪声特性,本文选用GZCORS 25个基准站观测数据作为实验数据。观测数据时间跨度为2017~2022年(5 a),采样率为30 s,全部配备Trimble NETR9型接收机和TRM59900.00 SCIS型天线。另外,为了将站坐标成果统一至ITRF2014框架下,在解算过程中引入中国及周边9个IGS站(BJFS、URUM、JFNG、WHUN、LHAZ、HKLS、HKWS、TWTF、CUSV)同时段数据。使用GAMIT/GLOBK10.71软件对GNSS数据进行基线处理和网平差,基线处理策略如表 1所示。
|
|
表 1 基线处理策略 Tab. 1 Baseline processing strategy |
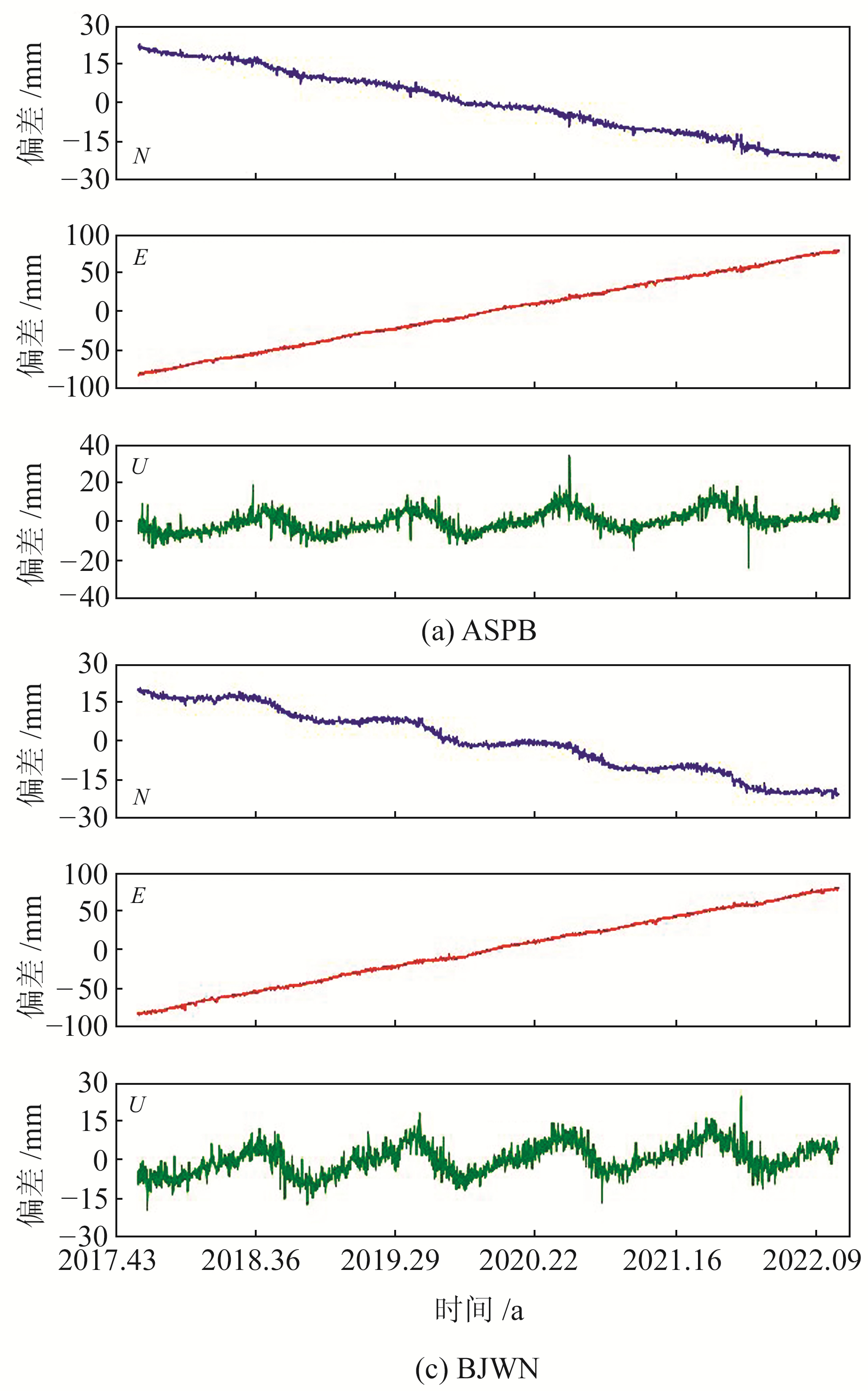
基线处理完成后,对其结果进行质量检核,所有单天解NRMS值均小于0.2,基线重复率拟合的相对精度为7.58×10-10,常数部分优于2 mm,基线解算质量满足要求。使用GLOBK软件在ITRF2014框架下进行整网平差,采用IGS提供的每周周解文件对应的9个IGS站坐标作为参考坐标进行整网平差,得到GZCORS基准站在ITRF2014框架下的单天解坐标时间序列,其中安顺平坝站(ASPB)、毕节威宁站(BJWN)等典型喀斯特地区站点时间序列如图 1所示。
|
图 1 部分喀斯特GNSS站点原始坐标时间序列 Fig. 1 Time series of original coordinates of some Karst GNSS stations |
本文采用如下步骤获取残差坐标时间序列:1)以单天解坐标时间序列作为输入,采用QOCA(quasi-observation combination analysis)软件analyze_tseri模块估计GNSS坐标时序模型[3](式(1))中速度项、周期项和阶跃式偏移量。2)在单天解坐标时间序列中扣除第一步估计得到的速度项、周期项和阶跃式偏移量等,得到初始残差坐标时间序列。3)由于外界条件、信号干扰等突变因素的影响,坐标时间序列中难免有奇异值存在,这些奇异值应在坐标时间序列中给予剔除,以免在噪声模型分析中造成偏差。本文奇异值剔除的标准如下:N、E、U三个分量中误差阈值分别设为30 mm、30 mm、50 mm,残差阈值分别设为100 mm、100 mm、200 mm。4)若某站点时间序列中存在奇异值,则以剔除奇异值之后的单天解坐标时间序列作为输入,重复以上步骤,直至满足要求为止。
| $ \begin{gathered} \Delta y\left(t_i\right)=y\left(t_i\right)-\left(a+b t_i+c \sin \left(2 \pi t_i\right)+\right. \\ d \cos \left(2 \pi t_i\right)+e \sin \left(4 \pi t_i\right)+f \cos \left(4 \pi t_i\right)+ \\ \left.\sum\limits_{j=1}^{n_g} g_i H\left(t_i-T_{g j}\right)\right) \end{gathered} $ | (1) |
式中,y(ti)为GNSS基准站坐标时序,ti代表第i个历元时间,以小数年的形式表示;a表示初始历元测站坐标;b表示速度项;c、d表示全年周期运动系数;e、f表示半年周期运动系数;g表示历元Tg处由于各种原因(如天线位置变化、站点形变、同震位移等)引起的阶跃式偏移量。
2 共模误差提取及特性分析 2.1 空间滤波提取共模误差共模误差是GNSS区域网中存在的一种时空相关误差,对区域网进行空间滤波可有效减少这种误差的影响[8-9]。本文利用QOCA软件,采用主成分分析法(principal component analysis,PCA)对区域网的残差坐标时间序列进行空间滤波,该方法不要求基准站网空间均匀分布,适合于大范围基准网的共模误差提取。
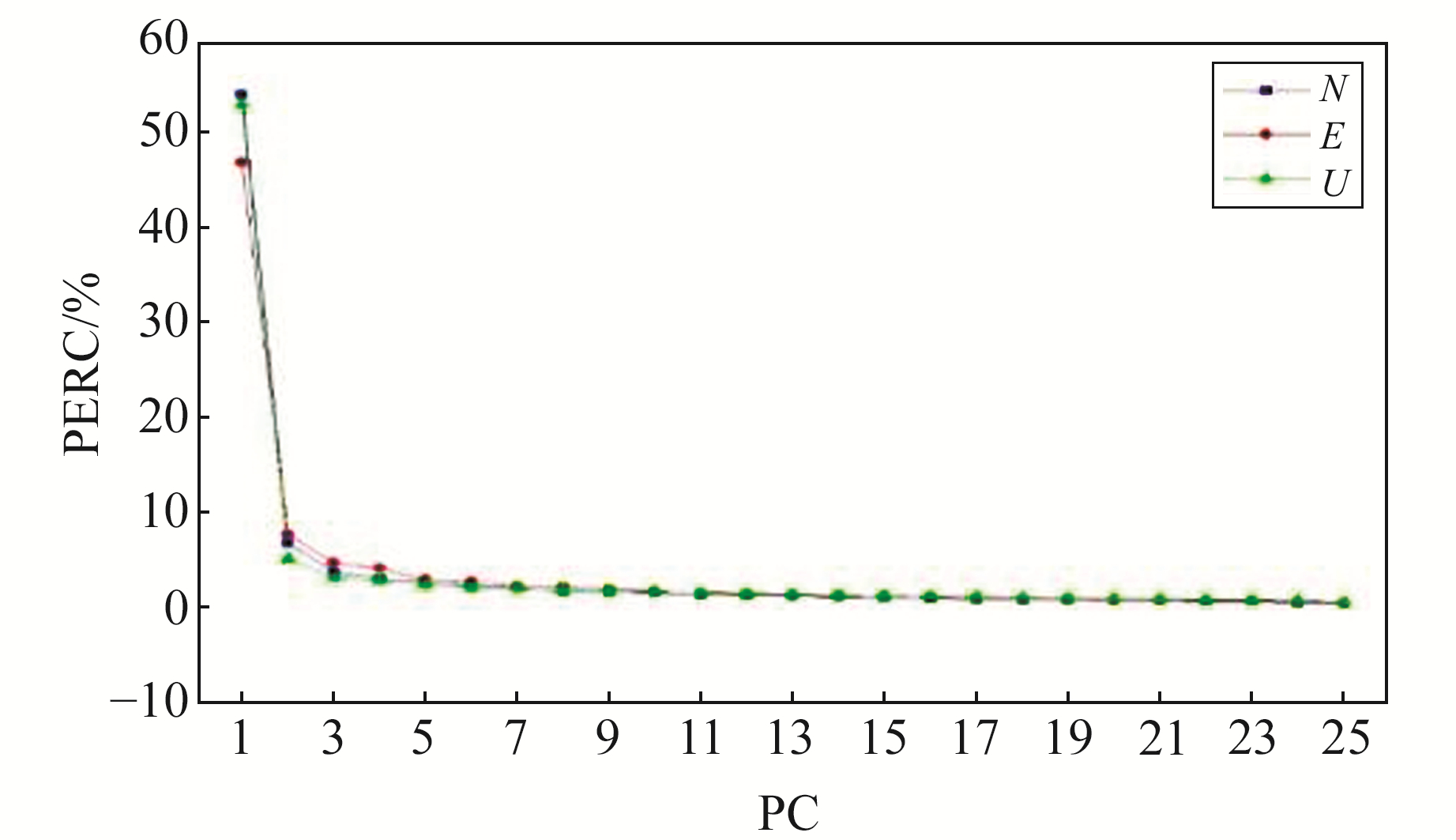
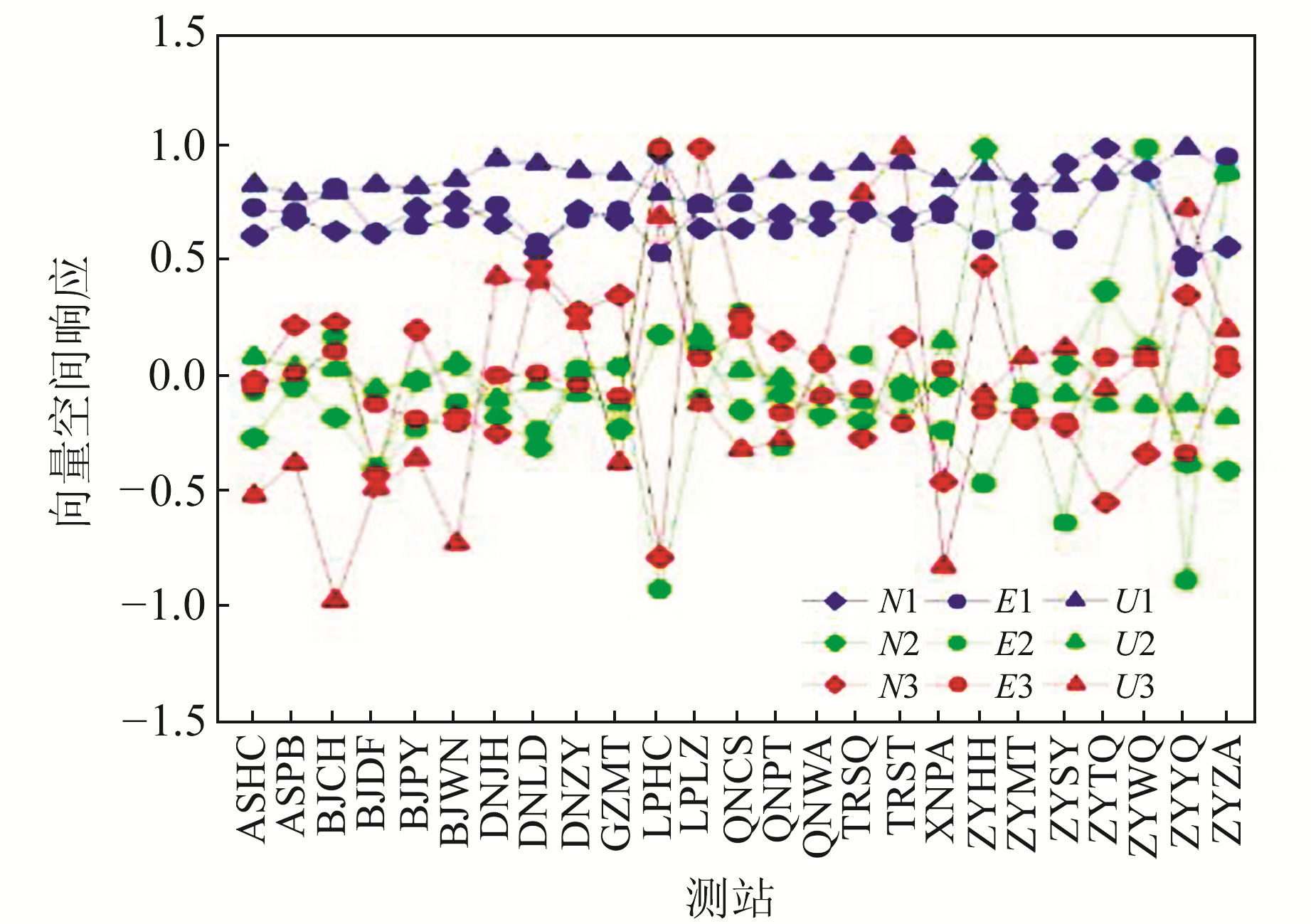
Dong等[5]将共模误差定义为:若某一主分量中大多数测站(多于50%)具有明显(大于0.25)的标准化空间响应,且其特征值超过所有特征值总和的1%,则认为具有共模误差。因此,本文从特征值占比和标准化空间响应两个方面进行显著性检验,以确定共模误差主分量个数。利用PCA方法对N、E、U分量的残差时间序列进行空间滤波处理,得到各主分量特征值占总特征值的百分比(图 2),以及各测站坐标序列分量前3阶主成分的标准化空间响应(图 3),标准化空间响应由各测站空间响应除以最大空间响应得到,正值代表对主成分的积极响应,负值代表对主成分的消极响应。由图 2和图 3(N、E、U代表方向,后面的数字代表阶次)可知,对于N、E、U坐标分量,第一主分量中所有测站的标准化空间响应均大于0.25,其特征值占总特征值的百分比分别为55%、47%、53.5%,满足共模误差定义的所有条件,更高阶主分量不能满足50%以上测站标准化空间响应大于0.25的条件。在特征值方面,第一主成分特征值显著大于其他主成分特征值,对整个残差时间序列的贡献十分显著。因此,N、E、U坐标分量均只采用第一主成分分量计算共模误差。
|
图 2 各主分量特征值占总特征值百分比 Fig. 2 The percentage of every principal component eigenvalue |
|
图 3 各测站前3阶主成分标准化空间响应 Fig. 3 Normalized spatial eigenvector of first three principal components |
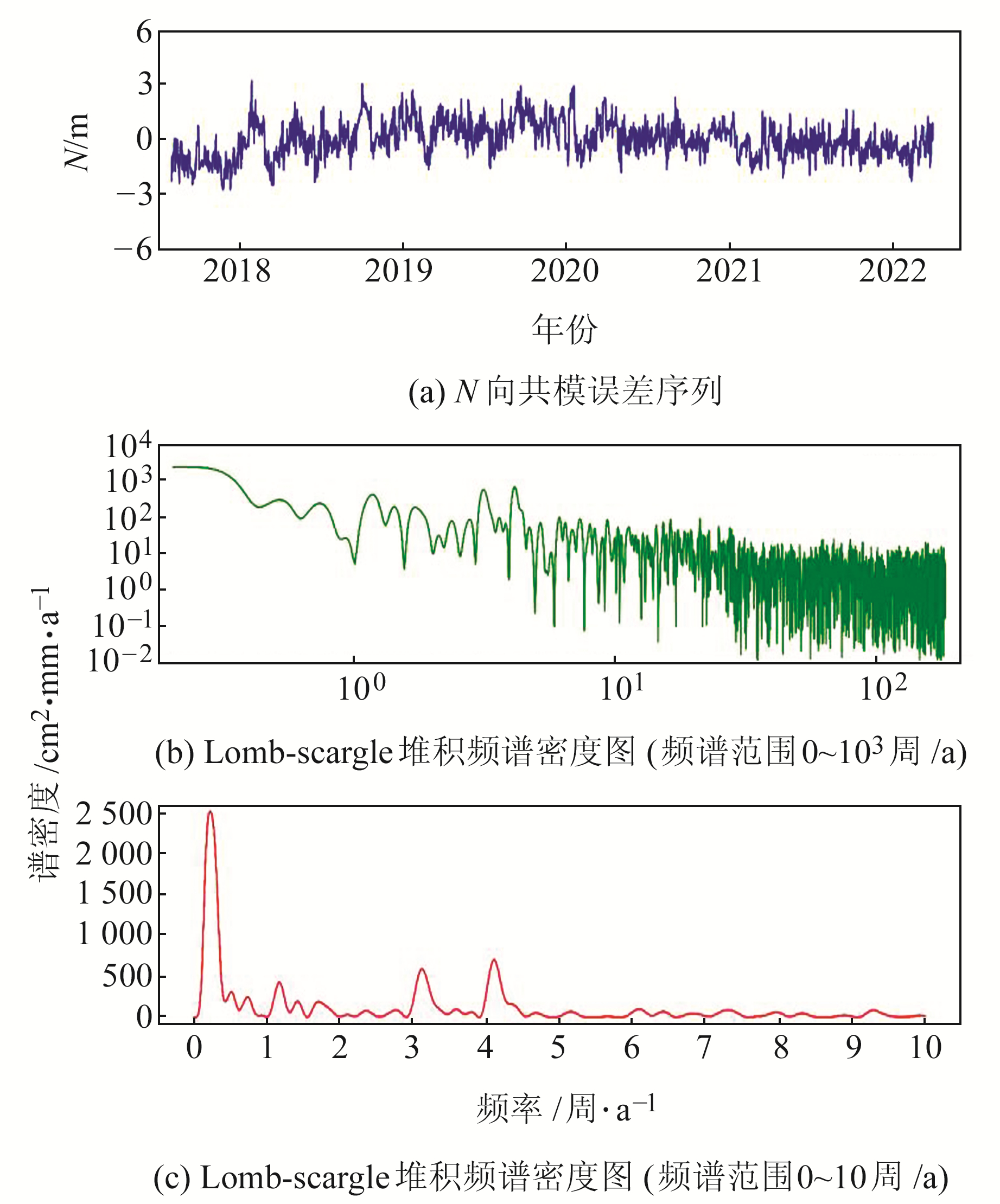
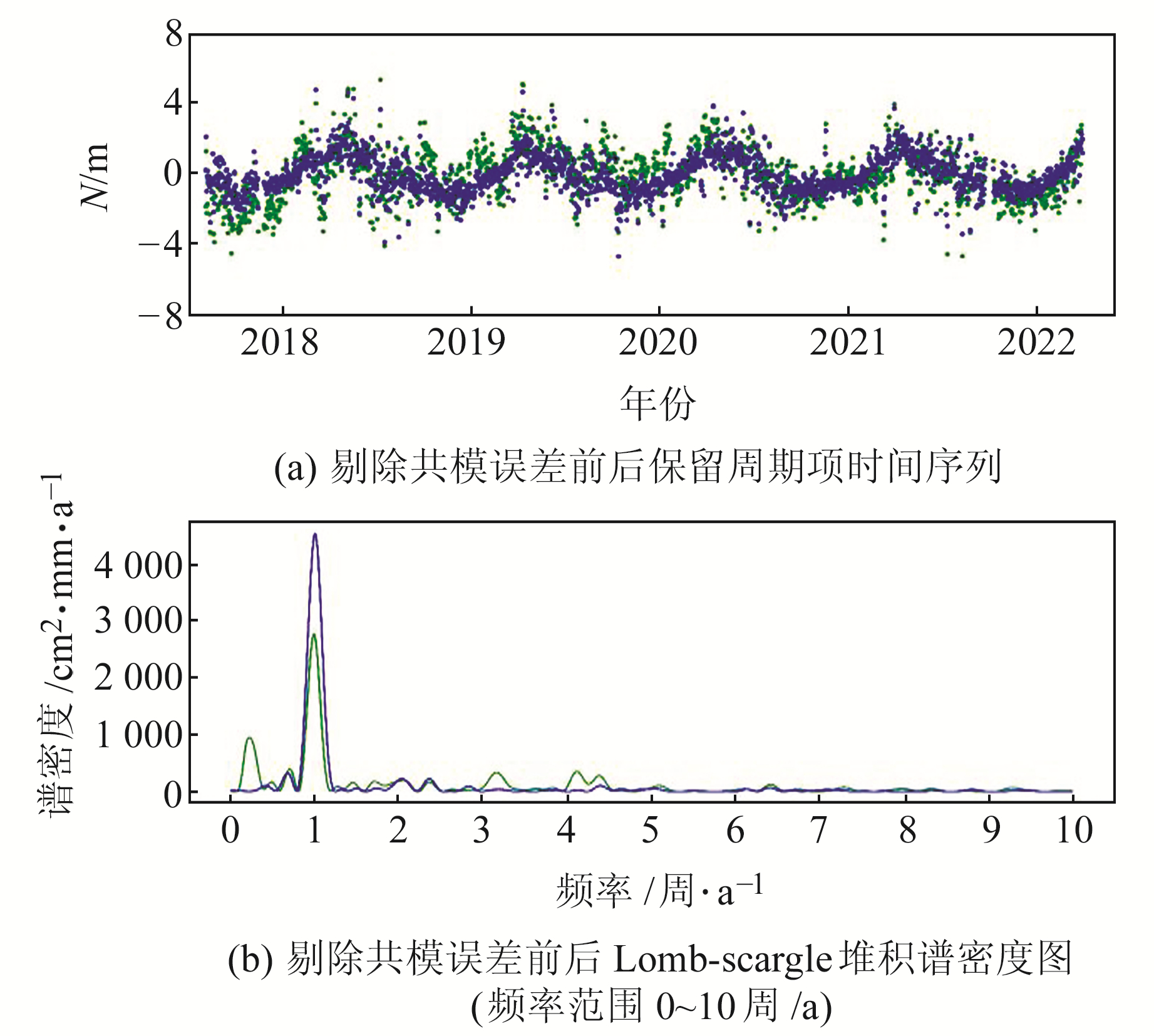
共模误差作为一种区域时空相关的公共误差,是整个区域内绝大部分站点都存在的多种误差集合,一般包括由于GNSS数据处理模型和策略不完善而引起的误差,以及在GNSS数据处理中未模型化的误差,如大气压负载、非潮汐海洋负载、积雪深度负载、土壤湿度负载等的地表质量负载影响。本文采用Lomb-scargle谱分析方法探测共模误差中的周期信号,得到各基准站共模误差序列的堆积频谱图,其中图 4为N方向共模误差序列及谱分析结果,发现N方向最大振幅周期分别出现在0.2周/a、1.2周/a、3.2周/a和4.2周/a,说明共模误差中包含有周期项。去除站点坐标时间序列的初始项、速度项和阶跃式偏移,并保留周期项,分析空间滤波前后坐标时间序列的谱密度指数变化情况,如图 5(绿色为剔除共模误差前的时间序列和谱密度,蓝色为剔除共模误差后的时间序列和谱密度)所示。由图 5可知,剔除共模误差后,坐标时间序列噪声水平明显降低,共模误差频谱图中0.2周/a、3.2周/a和4.2周/a等3个周期误差得到有效剔除,时间序列中年周期项谱密度也变得更加显著,有效降低了噪声的影响。
|
图 4 N方向共模误差序列及谱分析结果 Fig. 4 Common error and spectral analysis results of north |
|
图 5 DNZY站N方向剔除共模误差前后对比 Fig. 5 Spectral analysis results of DNZY before and after eliminating common errors in the north |
为确定各测站不同坐标分量的噪声特性,本文利用CATS软件[10],使用最大似然估计法对空间滤波前后坐标时间序列采用不同噪声模型组合的方式定量估计各测站不同坐标分量的噪声水平,逐个测站分析其最优噪声模型。大量研究结果表明,GNSS坐标时间序列除包含白噪声(white noise, WN)外,还可能包含其他有色噪声,如闪烁噪声(flicker noise,FN)、随机漫步噪声(random walk noise,RW)、幂律噪声(power law noise,PL)、一阶高斯-马尔科夫(first order Gauss-Markov,FOGM)等,本文利用CATS软件估计WN、WN+ FN、WN + RW、FN + RW、WN+ FN +RW、WN+ PL、WN+ FOGM等7种噪声模型下空间滤波前后坐标时间序列的速度项、周年及半周年振幅,采用Langbin提出的保守估计准则确定时间序列最优噪声模型[11-12]。
3.1 最优噪声模型确定使用上述7种模型计算空间滤波前后25个GNSS基准站N、E、U三分量的MLE值,然后确定每个测站各坐标分量时间序列的最优噪声模型。对于N方向,空间滤波前最优噪声模型WN+FN占比84%、WN+GM和WN+FN+RW各占比8%,空间滤波后最优噪声模型WN+FN占比80%、WN+GM占比16%、WN+FN+RW占比4%;对于E方向,空间滤波前最优噪声模型WN+FN占比88%、WN+GM占比4%、WN+FN+RW占比8%,空间滤波后最优噪声模型WN+FN占比56%、WN+GM占比36%、WN+FN+RW占比8%,最优模型中32%的站点由WN+FN转变为WN+GM;对于U方向,空间滤波前最优噪声模型WN+FN、WN+GM分别占比60%、40%,空间滤波后最优噪声模型WN+FN、WN+GM占比变为80%、20%,最优模型中20%的站点由WN+GM转变为WN+FN。总而言之,去除共模误差后,36%的测站分量噪声特性发生变化,E方向主要由WN+FN变为WN+GM,U方向主要由WN+GM变为WN+FN。
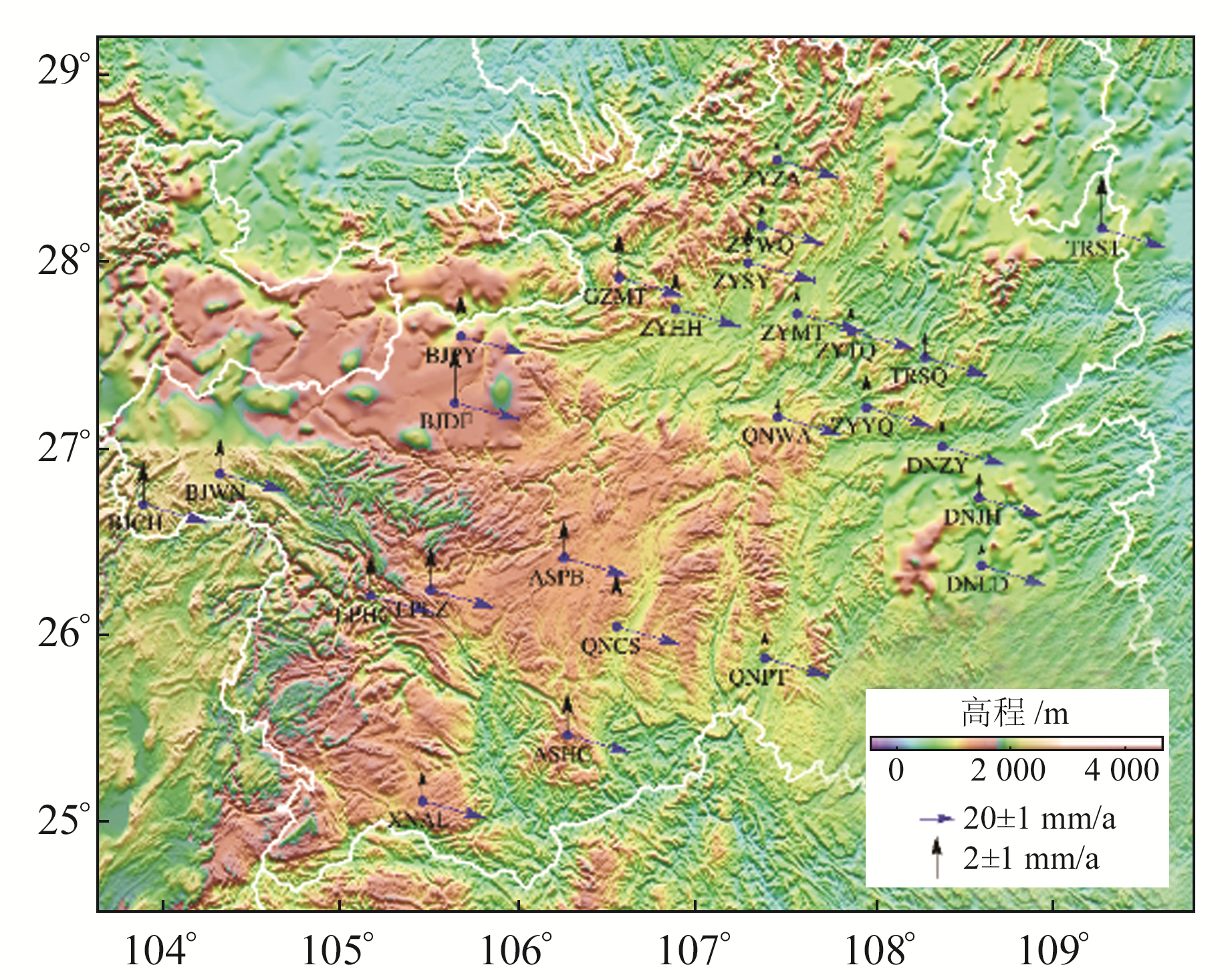
3.2 共模误差对站点速度估计的影响及其地形变方式分析首先基于单天解坐标时间序列生成残差坐标时间序列,利用PCA空间滤波方法提取共模误差;然后针对每个站点剔除其坐标时间序列中的共模误差,得到用于速度参数估计的站点坐标时间序列;最后基于最大似然估计法确定最优噪声模型,并采用最优噪声模型估计站点速度。根据给定的空间滤波前后各测站分量时间序列最优噪声模型,使用CATS软件估计得到空间滤波前后各测站分量在ITRF2014框架下的速度及其中误差,结果如表 2所示,绘制其速度场如图 6所示。由表可知,空间滤波后,各坐标分量速度参数的估计精度均有明显提升,其中N、E、U分量分别提高52%、56%和50%,说明剔除共模误差可有效降低时间序列模型参数的误差,从而提高坐标时间序列的精度。对于基准站水平方向,N方向的最大速度为-9.07 mm/a、最小速度为-10.46 mm/a、平均速度为-9.63 mm/a,E方向的最大速度为36.17 mm/a、最小速度为33.17 mm/a、平均速度为34.34 mm/a,计算得到水平方向最大运动速率为37.46 mm/a、最小运动速率为34.59 mm/a、平均运动速率为35.67 mm/a,运动方向为东偏南14.61°~16.98°,说明GZCORS基准站水平方向运动速率和方向均趋向于一致,受大陆板块内部断层相对运动影响较小。对于基准站垂直方向,贵州省陆地垂直运动总体表现为隆起趋势,最大隆起速率为2.4 mm/a、最小隆起速率为0.4 mm/a、平均隆起速率为1.5 mm/a。
|
|
表 2 空间滤波前后最优噪声模型下各站坐标的速度及中误差 Tab. 2 The velocity and variance under optimal noise model before and after spatial filtering |
|
图 6 贵州速度场分布 Fig. 6 Distribution of velocity field in Guizhou |
本文首先利用GAMIT/GLOBK软件处理25个GZCORS站点观测数据,得到单天解站点坐标时间序列。然后采用主成分分析法提取站坐标共模误差,并用于改正站点坐标时间序列。最后采用最大似然估计法确定各测站不同坐标分量的最佳噪声模型,并估计最佳噪声模型的站点速度。本文主要结论如下:
1) 为了分析共模误差的基本特性,采用Lomb-scargle谱分析方法得到共模误差序列的堆积频谱图,结果表明,N方向最大振幅周期分别出现在0.2周/a、1.2周/a、3.2周/a和4.2周/a,说明共模误差中包含有周期项。
2) 为了得到适应GZCORS坐标时间序列的最优噪声模型组合,采用最大似然估计法进行不同噪声模型估计。结果表明,GZCORS站点最优噪声模型以WN+FN和WN+GM为主,剔除共模误差后,36%的测站分量噪声特性发生变化,E方向主要由WN+FN变为WN+GM,U方向主要由WN+GM变为WN+FN。
3) 基于各测站分量时间序列最优噪声模型,采用极大似然法估计空间滤波前后各测站分量在ITRF2014框架下的速度及其中误差。结果表明,空间滤波后,各坐标分量速度参数的估计精度均有明显提升,其中N、E、U分量分别提高52%、56%和50%,说明剔除共模误差可有效降低时间序列模型参数的误差,提高坐标时间序列的精度。地形变方式方面,水平方向运动为东偏南14.61°~16.98°,垂直方向运动总体表现为隆起趋势。
| [1] |
Wdowinski S, Bock Y, Zhang J, et al. Southern California Permanent GPS Geodetic Array: Spatial Filtering of Daily Positions for Estimating Coseismic and Postseismic Displacements Induced by the 1992 Landers Earthquake[J]. Journal of Geophysical Research, 1997, 102: 18057-18070 DOI:10.1029/97JB01378
(  0) 0) |
| [2] |
王朝阳, 邢喆, 张峰, 等. 顾及共模误差的西南极GPS坐标时间序列噪声分析[J]. 大地测量与地球动力学, 2022, 42(2): 132-138 (Wang Zhaoyang, Xing Zhe, Zhang Feng, et al. Noise Analysis of the GPS Coordinate Time Series in the West Antarctic with Consideration of Common Mode Error[J]. Journal of Geodesy and Geodynamics, 2022, 42(2): 132-138)
(  0) 0) |
| [3] |
马超, 李斐, 张胜凯, 等. 顾及共性误差的南极半岛地区连续GPS站坐标时间序列分析[J]. 地球物理学报, 2016, 59(8): 2783-2795 (Ma Chao, Li Fei, Zhang Shengkai, et al. The Coordinate Time Series Analysis of Continuous GPS Stations in the Antarctic Peninsula with Consideration of Common Mode Error[J]. Chinese Journal of Geophysics, 2016, 59(8): 2783-2795)
(  0) 0) |
| [4] |
李斐, 马超, 张胜凯, 等. 南极半岛地区GPS坐标时间序列噪声分析及形变模式初探[J]. 地球物理学报, 2016, 59(7): 2402-2412 (Li Fei, Ma Chao, Zhang Shengkai, et al. Noise Analysis of the Coordinate Time Series of the Continuous GPS Station and the Deformation Patterns in the Antarctic Peninsula[J]. Chinese Journal of Geophysics, 2016, 59(7): 2402-2412)
(  0) 0) |
| [5] |
Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3)
(  0) 0) |
| [6] |
袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析[J]. 地球物理学报, 2008, 51(5): 1372-1384 (Yuan Linguo, Ding Xiaoli, Chen Wu, et al. Characteristics of Daily Position Time Series from the Hong Kong GPS Fiducial Network[J]. Chinese Journal of Geophysics, 2008, 51(5): 1372-1384 DOI:10.3321/j.issn:0001-5733.2008.05.011)
(  0) 0) |
| [7] |
吕成亮, 张胜凯, 沈飞, 等. 基于共性误差的CORS站坐标时间序列分析[J]. 大地测量与地球动力学, 2016, 36(1): 16-20 (Lü Chengliang, Zhang Shengkai, Shen Fei, et al. The Analysis of Coordinate Time Series of CORS Based on Common Mode Errors[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 16-20)
(  0) 0) |
| [8] |
周茂盛, 郭金运, 沈毅, 等. 基于多通道奇异谱分析的GNSS坐标时间序列共模误差的提取[J]. 地球物理学报, 2018, 61(11): 4383-4395 (Zhou Maosheng, Guo Jinyun, Shen Yi, et al. Extraction of Common Mode Errors of GNSS Coordinate Time Series Based on Multi-Channel Singular Spectrum Analysis[J]. Chinese Journal of Geophysics, 2018, 61(11): 4383-4395)
(  0) 0) |
| [9] |
谢树明, 潘鹏飞, 周晓慧. 大空间尺度GPS网共模误差提取方法研究[J]. 武汉大学学报: 信息科学版, 2014, 39(10): 1168-1173 (Xie Shuming, Pan Pengfei, Zhou Xiaohui. Research on Common Mode Error Extraction Method for Large-Scale GPS Network[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10): 1168-1173)
(  0) 0) |
| [10] |
Williams S D P. CATS: GPS Coordinate Time Series Analysis Software[J]. GPS Solutions, 2008, 12(2): 147-153
(  0) 0) |
| [11] |
Langbein J. Noise in Two-Color Electronic Distance Meter Measurements Revisited[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B4)
(  0) 0) |
| [12] |
Langbein J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada[J]. Journal of Geophysical Research, 2008, 113(B5)
(  0) 0) |
2. GNSS Research Centre, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2024, Vol. 44
2024, Vol. 44


