伸缩仪对气压短时扰动的响应非常灵敏,这会在一定程度上扰乱构造应变场的真实信息,影响地震前兆异常的可靠识别。有学者基于周期气压波对钻孔体应变的影响特征和规律、短时气压突变对定点地形变观测的影响特征与机理、气压扰动的数学改正方法及气压变化对伸缩仪日变资料的影响等进行过研究[1-7]。上述伸缩仪的气压干扰研究主要集中在小时值数据日、月频段内,而对分钟值数据中数分钟至数小时频段(或周期)影响的精细分析较少,尤其是短时高频成分。本文选用常熟台气压短时扰动典型时段的观测资料,通过小波分解、相关分析与回归分析,在时域和频域内分别求取伸缩仪测量值和气压的相关系数、气压影响系数,得到伸缩仪在各频段的响应特征曲线,然后使用MATLAB软件分离气压短时干扰信号,再重构伸缩仪观测数据,所得效果较好。本文研究结果对地震短临前兆异常的正确识别和有效提取具有一定的实用价值。
1 观测概况常熟地震台观测山洞位于单斜山南麓,山体走向NW,长轴5 km、短轴2.5 km,岩性为石英砂岩,最高峰海拔265 m。山洞原为军用,条件较好,主通道进深250 m、洞高2.35 m、宽2.50 m,混凝土全被覆,覆盖层厚20~30 m,日温差<0.03 ℃,年温差<0.3 ℃,常年温度在17.3 ℃,湿度100%。为防止气流干扰,在洞内安装有4道船舱水密门[8]。
原伸缩仪型号为SSY-Ⅱ型,于1996年开始观测,EW分量基线长24.19 m、方位角139.5°,NS分量基线长22.66 m、方位角32.4°,布设位置距洞口约210 m,仪器用泡沫板进行小腔体密封。2007年保留石英管基线,更换检测传感器和数字记录器后改造为SS-Y型伸缩仪,采样率为1次/min,同时安装了辅助气压计。
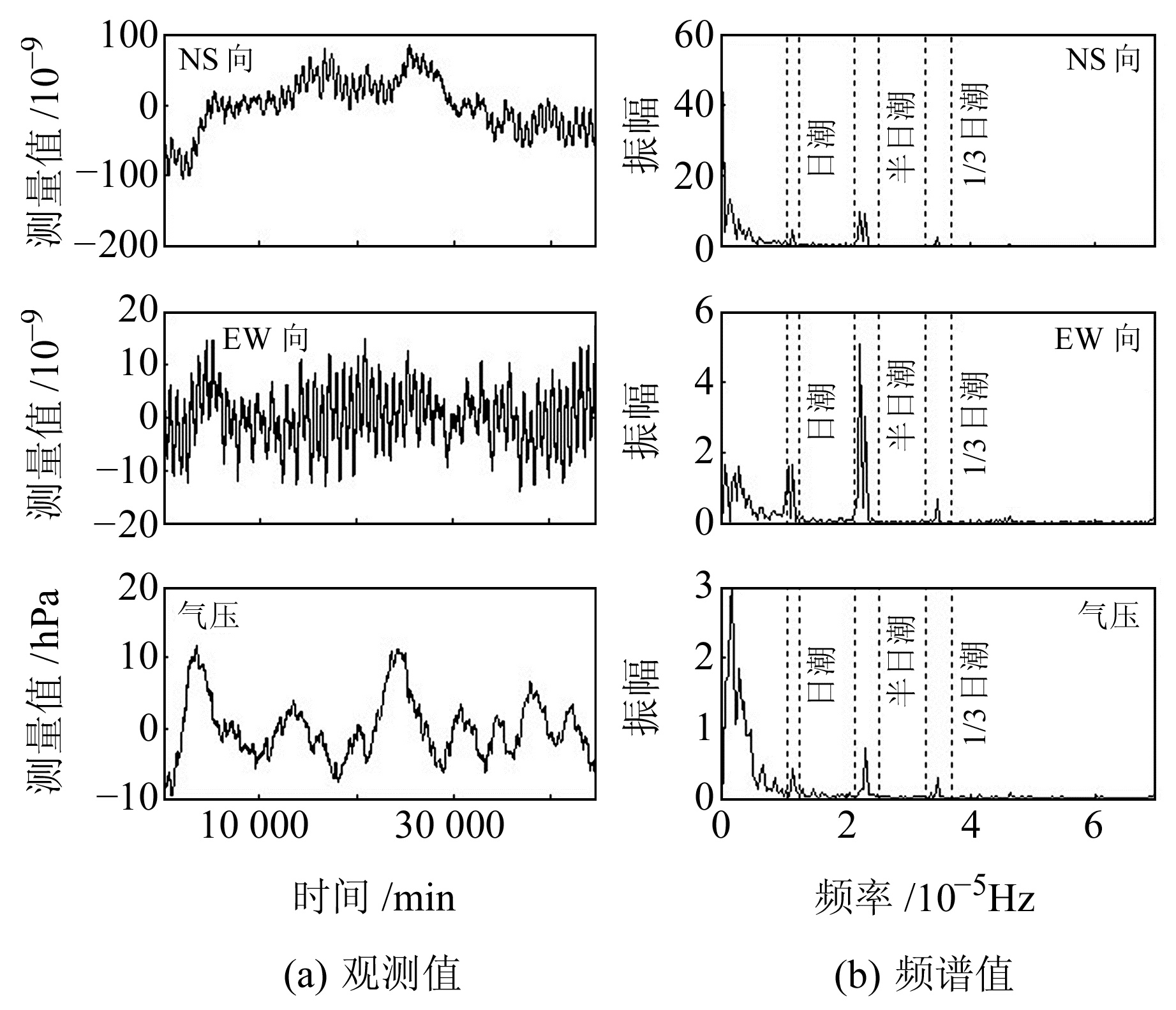
2 数据选取及分析方法常熟台伸缩仪记录到的固体潮日波、半日波变化清晰,为气压短时干扰研究提供了方便。选取2012~2018年分钟值观测数据,对其间无大地震、各种干扰因素较小的时段进行分析。运用快速傅里叶变换给出频率域成分,2013-01资料频谱分析结果显示(图 1),伸缩仪与气压数据中均含有明显的长周期潮、日潮、半日潮和1/3日潮等优势周期成分,而气压的短时扰动与这些大气潮汐变化无关。选取256 min以下的短周期数据,即可滤除这些信号。
|
图 1 常熟台伸缩仪观测数据及频谱分析 Fig. 1 Extensometer observation data and spectrum analysis at Changshu station |
小波变换及相关性分析是较为成熟的定量化信号处理技术,具备明显的频段特征,可作为分析非平稳信号的有力工具。利用小波变换分解后的结果可在不同的频率范围内计算相关参数,在不同频段下进行相关性比较,比用整体数据分析更加精细;利用小波分解与重构信号的方法,在干扰噪声频率范围已知的情况下,可有效分离信号和噪声的频带[8-9]。
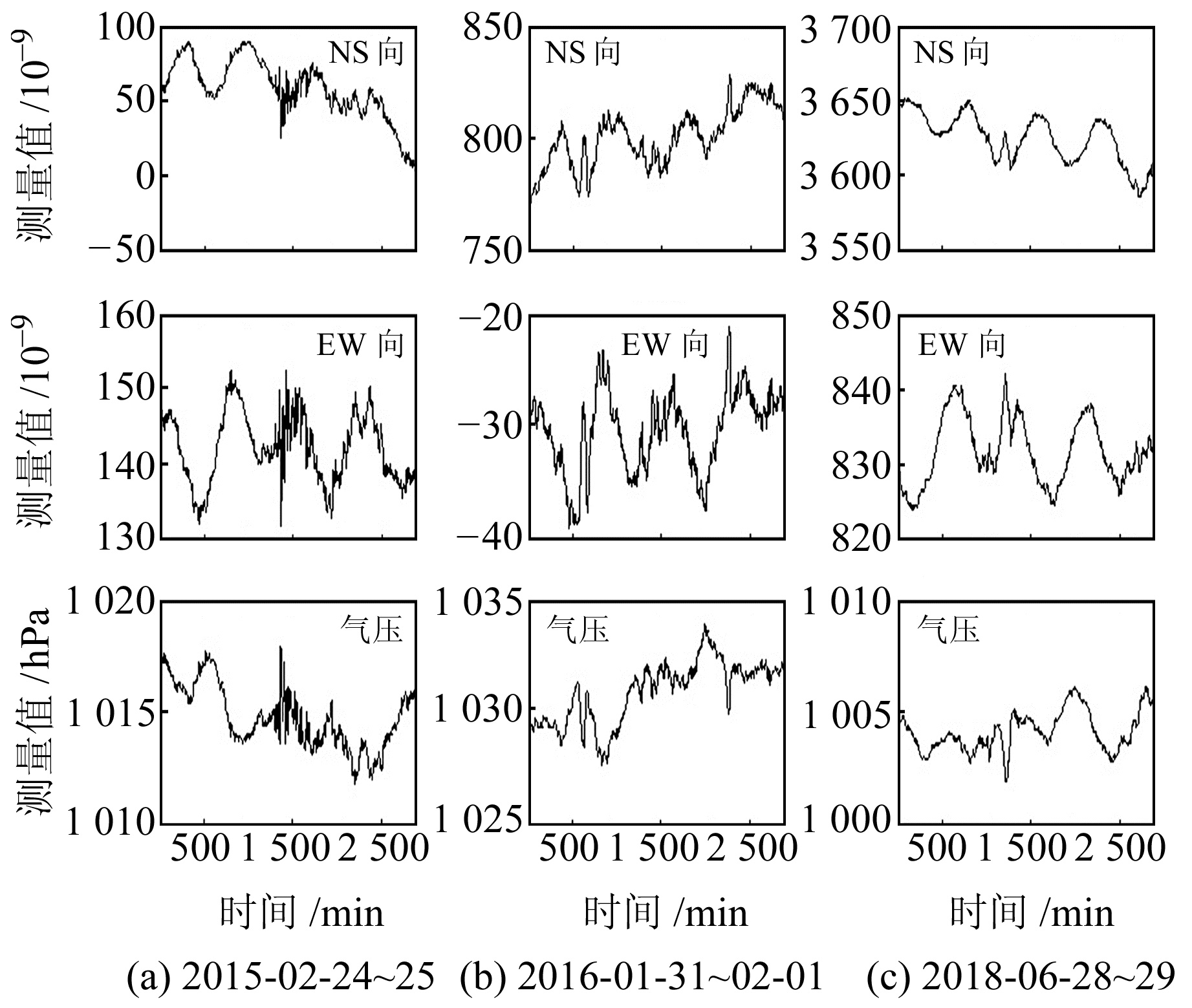
3 气压短时扰动对伸缩仪的影响特征与相关性分析图 2为气压短时扰动对伸缩仪观测影响的典型实例。可以看出,2个分量应变潮汐曲线上均出现同步反向畸变(抖动、上升、下降等),气压变化越剧烈,畸变越显著,称该现象为气压非平稳时段,反之为气压平稳时段。计算图 2中常熟台伸缩仪NS、EW分量原始数据与气压的相关系数,分别为:0.04,-0.32(图 2(a));0.21,-0.18(图 2(b));-0.52,0.07(图 2(c))。计算结果表明,在固体潮背景下,直接利用伸缩仪整体数据分析其与短时气压波动的相关性效果不理想。
|
图 2 气压短时扰动的典型实例 Fig. 2 Typical interference diagram of short-term air pressure disturbance |
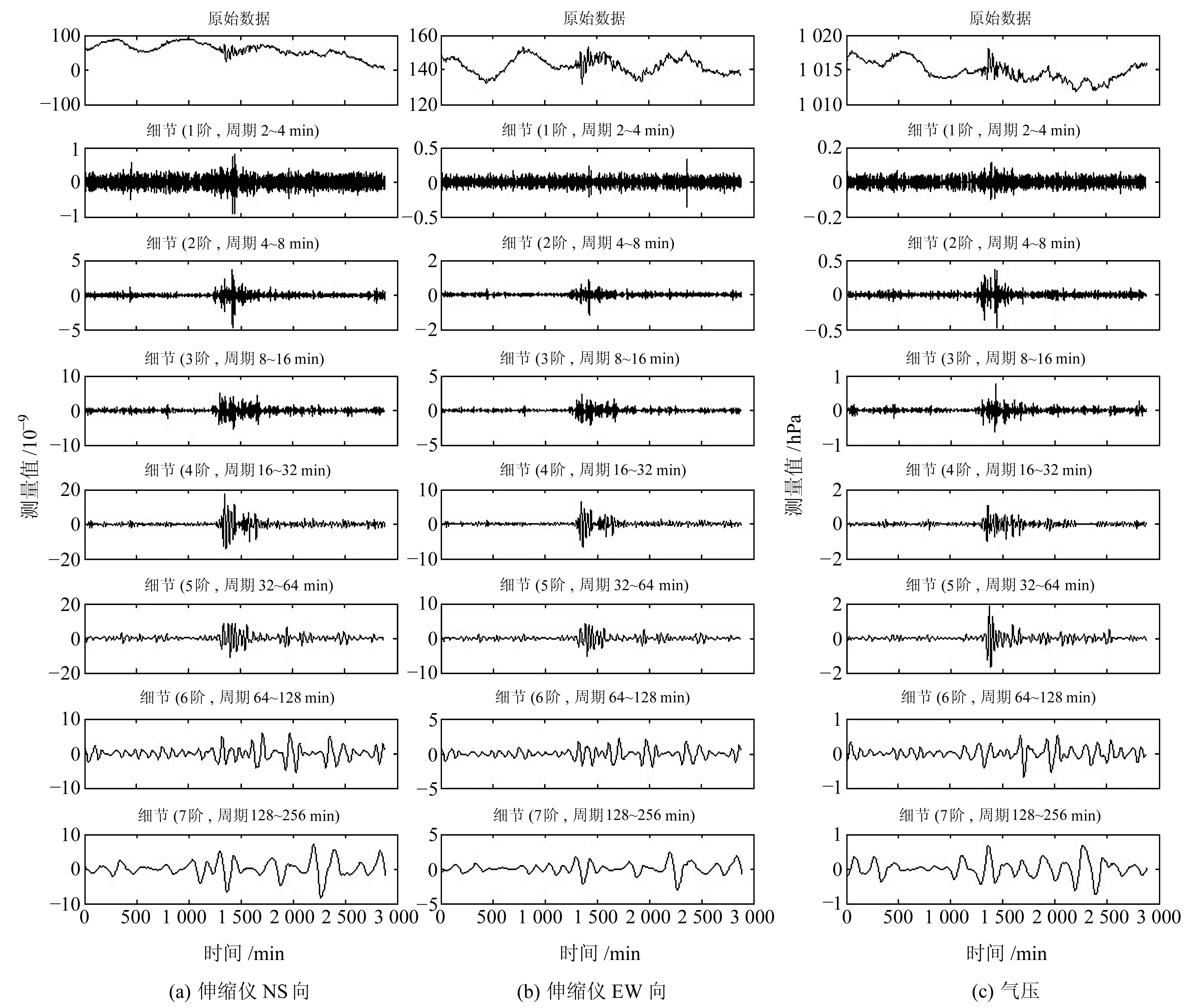
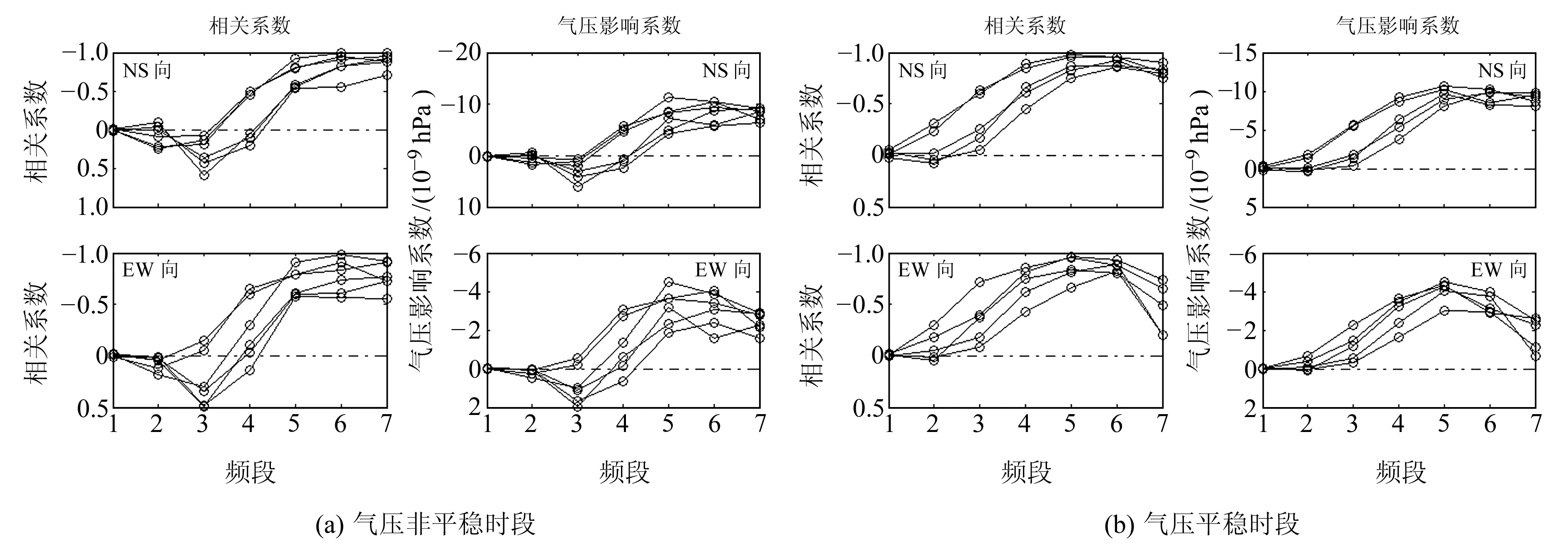
小波变换是将信号按照不同频率进行分解,噪声干扰信号主要集中在高频部分,反映的是短期变化过程。因此,用小波分析方法将伸缩仪观测值中的短周期信号分离出来,这样气压影响会变得清晰[2],再通过相关性分析可揭示气压的影响特征。由于固体潮等因素的影响,形变观测数据由一系列不同频率的周期成分和背景噪声叠加组成,规律性较明显,在小波分析时选用正则性较好的db小波进行分析[10-11]。根据针对定点形变数据的小波基函数优劣研究结果[12]和综合对比计算,采用db4小波基函数进行离散变换,并在图 2基础上再增选3组气压短时扰动非平稳时段的数据(表 1),分别按2~4 min、4~8 min、8~16 min、16~32 min、32~64 min、64~128 min、128~256 min的周期进行分解。图 3为图 2(a)分解后的高频波形,展示了7个频段的气压影响信号。进一步将同一频段的波形分别作相关分析与线性回归分析,得到全部频段的相关系数与气压影响系数(图 4(a))。为进行对比,选取6组气压平稳时段的观测值(表 1),用相同方法处理后得出相应的相关系数及气压影响系数曲线(图 4(b))。考虑到观察方便,图 4中相关系数与气压影响系数均采用反向直角坐标。
|
|
表 1 数据选取时段 Tab. 1 Data selection period |
|
图 3 伸缩仪与气压数据小波分解高频波形 Fig. 3 High-frequency waveform of wavelet decomposition of extensometer and air pressure data |
|
图 4 气压非平稳时段与平稳时段的相关系数和气压影响系数 Fig. 4 Correlation coefficient and air pressure influence coefficient between non-stationary period and stationary period of air pressure |
由图 4可以看出,气压平稳时段6组样本的相关系数与气压影响系数曲线较为光滑,波动较小,规律性较强;气压非平稳时段的曲线波动明显较大。
离散系数是衡量数据离散程度的相对指标,其值越大,数据的离散程度也越大,其计算公式为[13]:
| $ c=\frac{\sigma}{\mu} $ | (1) |
式中,c为离散系数,σ为数据的标准差, μ为数据的平均值。图 5和6分别给出各频段相关系数与气压影响系数的平均值及其离散系数,其中,相关系数及气压影响系数均采用反向直角坐标。

|
图 5 各频段气压相关系数平均值及其离散系数 Fig. 5 Average values of air pressure correlation coefficient and its dispersion coefficient of each frequency band |
|
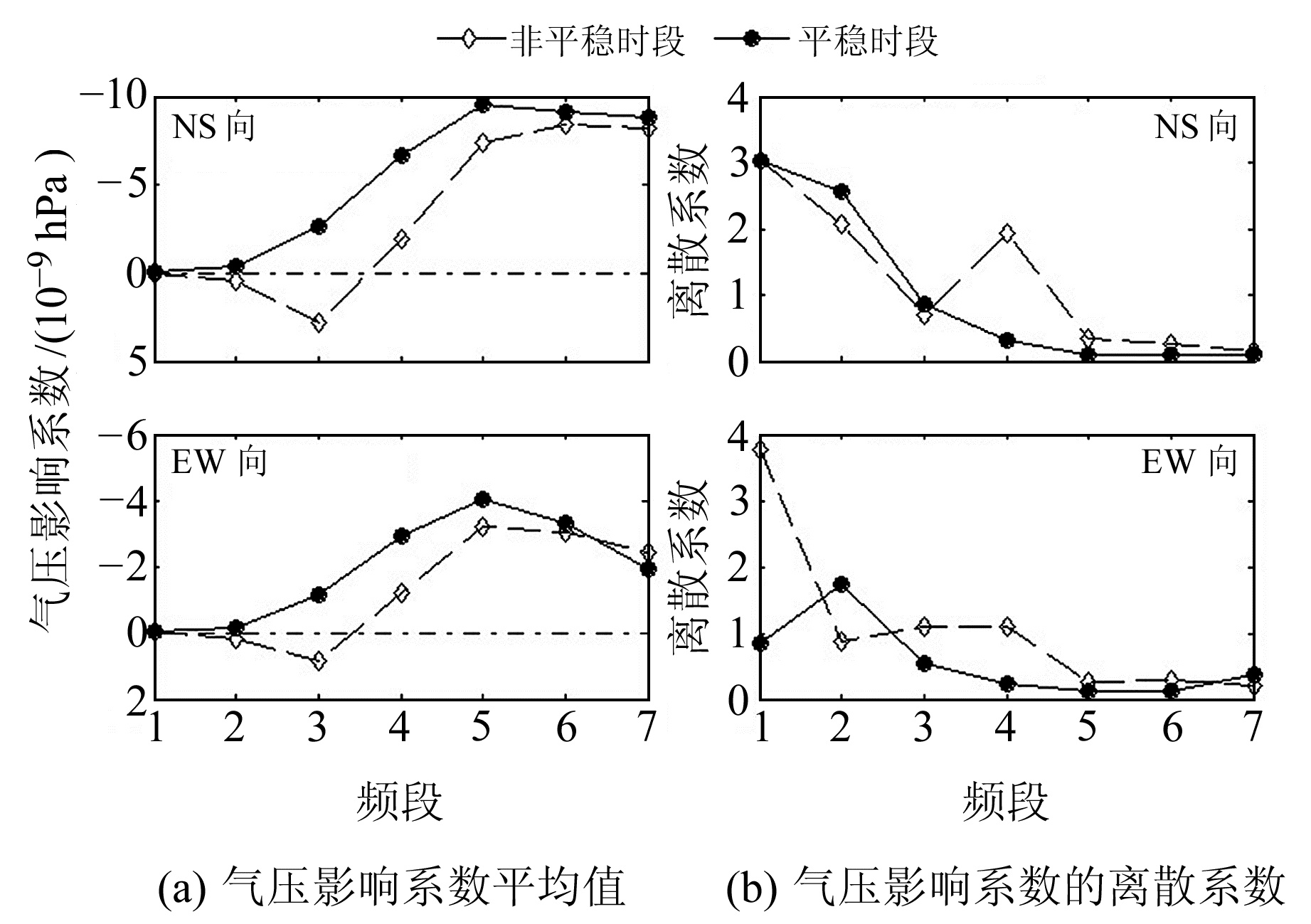
图 6 各频段气压影响系数平均值及其离散系数 Fig. 6 Average values of air pressure influence coefficient and its dispersion coefficient of each frequency band |
从图 4~6和表 2可以看出,伸缩仪2个分量在气压平稳时段的特征为:相关系数和气压影响系数在整个频段均为负值,其绝对值随周期增加而增大,第3频段(周期8~16 min)是一个过渡点,之前曲线上升较慢,相关性较差,之后曲线快速达到峰值且变化较为平稳;4条离散系数曲线与相关系数和气压影响系数同步变化但方向相反,即随频段增加而下降,表明离散程度在减小。气压在非平稳时段的特征为:1~3频段(周期≤16 min)2种系数都是正值,之后转为负值,第3频段是转折点;第4频段离散程度高,点位跳跃较大,相关系数和气压影响系数的绝对值均明显小于气压平稳时段,这可能与气压突变产生的动力学效应有关;第5~7频段(周期32~256 min)2种系数的绝对值基本都略小于气压平稳时段。
|
|
表 2 气压影响系数平均值 Tab. 2 Average values of air pressure influence coefficient |
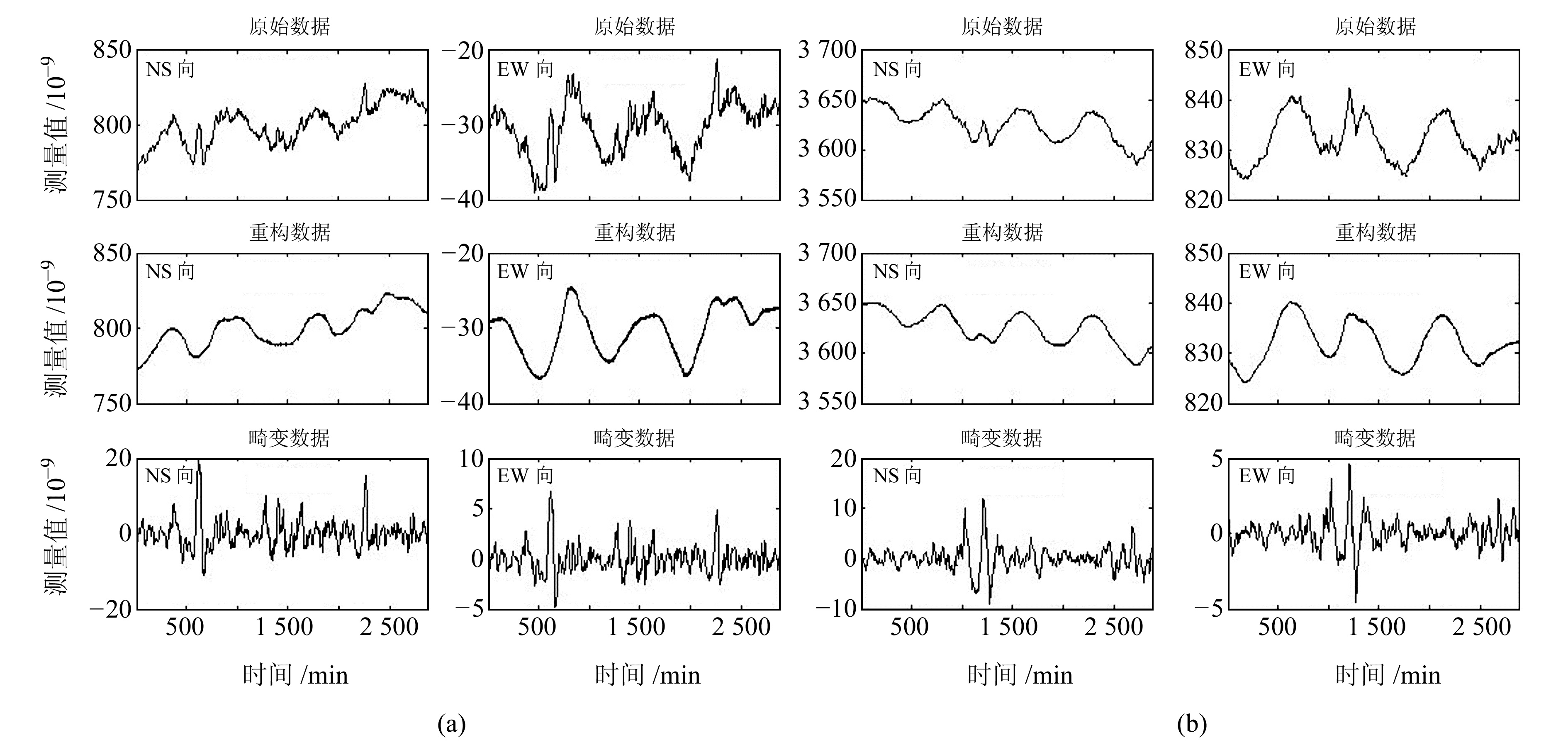
目前主要采用线性回归方法排除气压对伸缩仪的影响,即计算气压对伸缩仪整体数据的影响系数后进行相应改正,但短时气压波动剧烈时,该方法效果不理想。本文选取图 2中部分气压短时扰动典型时段的数据,使用MATLAB软件进行小波变换、相关分析及回归分析。首先进行小波分解,得出不同频段气压对伸缩仪的影响,然后剔除畸变明显频段的数据,再利用逆小波变换方法重构非气压影响频段数据,得到消除短时气压扰动的伸缩仪重构数据(图 7)。从表 3可知,直接将图 7中伸缩仪各分量原始值与气压进行相关性分析,相关系数低;而将伸缩仪各分量数据原始值减去重构数据得到的气压干扰成分(畸变数据)与去除周期成分的气压高频数据进行相关性分析,二者相关系数绝对值大于0.8。说明采用分频段计算方法可有效提取并排除伸缩仪的气压短时扰动影响。
|
图 7 消除气压短时干扰后的数据 Fig. 7 Data after eliminating short-term interference of air pressure |
|
|
表 3 原始数据和畸变数据与气压的相关系数 Tab. 3 Correlation coefficient between original data, distorted data and air pressure |
从图 7看出,重构后的伸缩仪曲线没有了由短时气压波动引起的上下突跳、毛刺等畸变现象,曲线变得光滑清晰,数据信噪比明显提升。
5 气压短时扰动对伸缩仪的影响机制探讨气压对定点形变观测的干扰途径有2种:1)作用于地壳表面,因负载效应产生间接影响;2)直接作用于仪器本体。常熟台观测山洞密封性较好,多道船舱水密门完全隔绝洞室与外界的空气流动,加之伸缩仪距洞口较远,因此外界气压波动无法直接作用于伸缩仪,而是通过洞体起作用。
气压平稳变化时,伸缩仪2个分量与气压的相关系数、气压影响系数在2~256 min周期内都表现为负值,说明气压影响机制相同,即气压增大使伸缩仪收缩(曲线向下),反之则是拉伸。气压非平稳时段的影响机制较复杂,周期小、幅度大的气压突变会导致地表瞬时变形[4],引起岩体应力的改变,从而影响应变测值。气压突变的产生通常有2种情况:一是雨季雷暴[14],为闪电伴随雷声的大气放电现象,属于局部地区强对流性天气,放电过程中温度骤增,使空气体积急剧膨胀,导致气压突变;二是大风(飓风、台风和气旋等),特点是速度快(超过17 m/s)、时间短,大风会引起山洞内空气振荡,产生气流扰动,从而对应变观测产生影响[15-16]。当周期为16~32 min时,气压非平稳时段的气压影响系数与气压平稳时段不同,其呈现由正值向负值过渡,这可能与气压的动力学效应有关。气压对NS分量影响大于EW分量,可能与山体的走向和局部地形有关。
6 结语1) 在气压短时扰动阶段,周期为8 min以下时,气压对伸缩仪的影响弱;周期为8 min以上时,气压对伸缩仪产生显著影响。周期在8~32 min时,伸缩仪观测量与气压的相关系数、气压影响系数均由正变负;周期在32~256 min之间时,伸缩仪观测量与气压的相关系数、气压影响系数较高且趋于平稳,离散系数小。因此气压短时波动对常熟台伸缩仪观测有显著影响的周期为8~256 min。
2) 气压短时扰动对常熟台伸缩仪观测在不同频段的影响机制存在差异性,周期小于16 min时,气压与伸缩仪观测量呈现正相关,相关性较差;反之为负相关,相关性较强。
3) 气压非平稳时段与平稳时段的不同主要为:周期在16 min以下时,前者伸缩仪观测量与气压相关系数、气压影响系数都是正值,之后才转为负值;周期在16~32 min时,前者离散系数较大,点位出现跳跃,2种系数绝对值明显小于后者,这可能与气压突变产生的动力学效应有关;周期在32~256 min时,前者2种系数绝对值基本都略小于后者。气压对伸缩仪NS分量的影响大约是EW分量的2.5~3倍,这可能与仪器观测点所处的山体走向和局部地形有关,有待进一步分析。
| [1] |
姜振海, 史小平. SSY-Ⅱ石英伸缩仪与SS-Y伸缩仪的对比分析[J]. 地震研究, 2010, 33(1): 63-67 (Jiang Zhenhai, Shi Xiaoping. Comparative Analysis of the SSY-Ⅱ Quartz Extensometer and the SS-Y Extensometer[J]. Journal of Seismological Research, 2010, 33(1): 63-67)
(  0) 0) |
| [2] |
周龙寿, 邱泽华, 唐磊. 地壳应变场对气压短周期变化的响应[J]. 地球物理学进展, 2008, 23(6): 1 717-1 726 (Zhou Longshou, Qiu Zehua, Tang Lei. The Response of Crustal Strain Field to Short-Period Atmospheric Pressure Variation[J]. Progress in Geophysics, 2008, 23(6): 1 717-1 726)
(  0) 0) |
| [3] |
张凌空, 王广才, 牛安福. 周期气压波对地壳应变场观测影响的若干因素分析[J]. 地震学报, 2011, 33(3): 351-361 (Zhang Lingkong, Wang Guangcai, Niu Anfu. Analysis on Several Factors of Periodic Air Pressure Wave Affecting Crustal Strain Field[J]. Acta Seismologica Sinica, 2011, 33(3): 351-361)
(  0) 0) |
| [4] |
杨小林, 危自根, 杨锦玲, 等. 飑线对定点地形变观测的影响特征与机理——以陕西关中盆地为例[J]. 中国地震, 2019, 35(3): 465-475 (Yang Xiaolin, Wei Zigen, Yang Jinling, et al. Ground Deformation Induced by a Strong Squall Line: A Case Study in the Weihe Basin, Shaanxi Province[J]. Earthquake Research in China, 2019, 35(3): 465-475)
(  0) 0) |
| [5] |
卢双苓, 林秀娜, 邢伟伟, 等. 泰安地震台伸缩仪运行分析[J]. 地震地磁观测与研究, 2011, 32(4): 83-89 (Lu Shuangling, Lin Xiuna, Xing Weiwei, et al. Operation Status Analysis of Extensometer at Tai'an Fiducial Seismic Station[J]. Seismological and Geomagnetic Observation and Research, 2011, 32(4): 83-89)
(  0) 0) |
| [6] |
樊冬, 尹传兵, 李惊生, 等. SS-Y型伸缩仪气压扰动影响的特征分析与数学改正[J]. 大地测量与地球动力学, 2017, 37(12): 1 313-1 316 (Fan Dong, Yin Chuanbing, Li Jingsheng, et al. Analysis Disturbance Characteristics from Air Pressure Change and Mathematical Correction of SS-Y Tensometer[J]. Journal of Geodesy and Geodynamics, 2017, 37(12): 1 313-1 316)
(  0) 0) |
| [7] |
张文来, 罗宏江, 苏萍. 气压变化对SS-Y伸缩仪观测日变曲线的干扰分析[J]. 内陆地震, 2006, 20(3): 266-270 (Zhang Wenlai, Luo Hongjiang, Su Ping. The Interferential Analysis on Air Pressure Change toward Observational Daily Change Curve of SS-Y Tensometer[J]. Inland Earthquake, 2006, 20(3): 266-270)
(  0) 0) |
| [8] |
狄梁, 陈洪军, 冯志生, 等. 常熟地震台形变观测仪数字化改造[J]. 地震地磁观测与研究, 2003, 24(4): 92-95 (Di Liang, Chen Hongjun, Feng Zhisheng, et al. Digitalized Reformation of Deformation Observation in Changshu Seismic Station[J]. Seismological and Geomagnetic Observation and Research, 2003, 24(4): 92-95)
(  0) 0) |
| [9] |
宋治平, 武安绪, 王梅, 等. 小波分析方法在形变数字化资料处理中的应用[J]. 大地测量与地球动力学, 2003, 23(4): 21-27 (Song Zhiping, Wu Anxu, Wang Mei, et al. Application of Wavelet Transform to Analysis of Digital Deformation Data[J]. Journal of Geodesy and Geodynamics, 2003, 23(4): 21-27)
(  0) 0) |
| [10] |
原永东, 周锐, 莫佩婵, 等. 基于小波分析的水位观测气压效应研究[J]. 地震, 2017, 37(4): 162-172 (Yuan Yongdong, Zhou Rui, Mo Peichan, et al. Wavelet Analysis of Barometric Pressure Effects on Groundwater Level[J]. Earthquake, 2017, 37(4): 162-172)
(  0) 0) |
| [11] |
李杰, 刘希强, 李红, 等. 利用小波变换方法分析形变观测资料的正常背景变化特征[J]. 地震学报, 2005, 27(1): 33-41 (Li Jie, Liu Xiqiang, Li Hong, et al. Analyses on Normal Background Characteristics about Deformation Observation Data on the Basis of Wavelet Transform Method[J]. Acta Seismologica Sinica, 2005, 27(1): 33-41)
(  0) 0) |
| [12] |
刘建明, 李志海, 孙甲宁, 等. 基于小波分析提取地倾斜异常特征[J]. 地震, 2016, 36(1): 38-48 (Liu Jianming, Li Zhihai, Sun Jianing, et al. Extraction of Ground Tilt Anormalies Based on Wavelet Analysis[J]. Earthquake, 2016, 36(1): 38-48)
(  0) 0) |
| [13] |
张萌物. 对离散系数定义及公式的完善与改进[J]. 西安石油学院学报: 社会科学版, 1999, 8(2): 55-56 (Zhang Mengwu. Perfection and Improvement of the Definition and Formula of Discrete Coefficient[J]. Journal of Xi'an Petrdleum Institute: Social Sciences Edition, 1999, 8(2): 55-56)
(  0) 0) |
| [14] |
张凌空, 吴利军, 杨颖. 雷暴产生的气压突变对体应变与同井水位干扰的对比研究[J]. 中国地震, 2012, 28(1): 69-77 (Zhang Lingkong, Wu Lijun, Yang Ying. Comparative Study of the Interference of Mutation Pressuregenerated by Thunderstorms with Volume Strain and Same Wellwater-Level[J]. Earthquake Research in China, 2012, 28(1): 69-77)
(  0) 0) |
| [15] |
王梅, 李峰, 孔向阳, 等. 数字化形变观测干扰识别[J]. 大地测量与地球动力学, 2004, 24(1): 94-98 (Wang Mei, Li Feng, Kong Xiangyang, et al. Identification of Disturbance of Digital Deformation Observations[J]. Journal of Geodesy and Geodynamics, 2004, 24(1): 94-98)
(  0) 0) |
| [16] |
陈德福. 地壳形变动力学观测与研究[M]. 北京: 海洋出版社, 1933 (Chen Defu. Observation and Research on the Dynamics of Crustal Deformation[M]. Beijing: China Ocean Press, 1933)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


