大气水汽在大气中的占比仅为0.1%~3%,却是大气中最活跃的成分[1],其含量与分布和降雨密切相关。传统大气水汽探测手段,如水汽辐射计、无线电探空仪等仪器昂贵、时空分辨率低。地基GNSS技术凭借其高精度、低成本、全天候、高时空分辨率等优点,在大气水汽探测、大气可降水量(PWV)反演等领域得到广泛应用[2]。天顶对流层湿延迟(zenith wet delay, ZWD)和转换系数K是反演PWV的关键参量,而大气加权平均温度Tm是计算K值的唯一变量,因此Tm值的精度会极大影响PWV的精度。由探空数据或大气再分析资料可以获得较高精度的Tm信息,但难以满足时效性和高时空分辨率的需要。因此,诸多学者建立了适用于部分区域或全球的Tm模型。
根据是否需要实测气象参数,可大致将Tm模型分为2类:非实测气象参数Tm模型和实测气象参数Tm模型。Emardson等[3]首次构建适用于欧洲范围的非实测气象参数Tm模型(Emardson模型),该模型在欧洲范围表现出良好的精度;文献[4-7]根据欧洲中期天气预报中心(ECMWF)的大气再分析资料建立和优化GPT系列模型,并被广泛使用。此类模型由多年Tm数据拟合而来,在难以获取实测气象参数的地区也能提供Tm值。然而该类模型多采用固定相位和振幅的三角函数模拟Tm的季节变化,忽略了其在不同年份间的变化,且无法体现天气变化对Tm的影响,因此非实测气象参数Tm模型的精度受到限制。
对于实测气象参数Tm模型,目前应用最广泛的是Bevis模型[8],该模型是以地表温度Ts为变量的一元线性模型。此后,学者们在建立实测气象参数Tm模型时发现,地表水汽压es与Tm同样存在强相关性,且Tm与Ts间的函数关系会随着纬度和高程的变化而变化,从而对Tm的计算精度产生影响[9-12]。研究表明,使用非线性函数描述Tm和Ts间的关系可取得精度更高的结果[13]。由以上研究可知,影响Tm的因素众多,这些因素与Tm间的函数关系复杂,且Tm存在明显的半年周期和年周期特性,很难简单地用线性函数或周期函数进行描述。鉴于机器学习方法具有良好的多参数非线性拟合能力,学者们先后建立了基于机器学习方法的Tm模型。Ding[14]首次尝试通过BP神经网络建立全球范围的Tm模型,并获得了比GPT2w模型更高的精度。Sun等[15]分别使用随机森林算法(RF)、广义回归神经网络(GRNN)和BP神经网络(BPNN)建立了中国区域需要实测气象参数的Tm模型,结果表明,3种机器学习方法均表现出比GPT3模型更高的精度。以上研究表明,使用机器学习方法建立Tm模型具有可行性。在众多机器学习方法中,BP神经网络凭借其结构简洁、易于实现等优点,常被用于建立Tm模型,然而BP神经网络存在全局寻优能力较差、易陷入局部最优的缺点。针对该问题,本文将全局寻优能力较强的粒子群优化算法(particle swarm optimization, PSO)[16]与BP神经网络结合,建立一种适用于中国区域、顾及多种影响因子的Tm模型PSOTM,并对其精度进行验证。
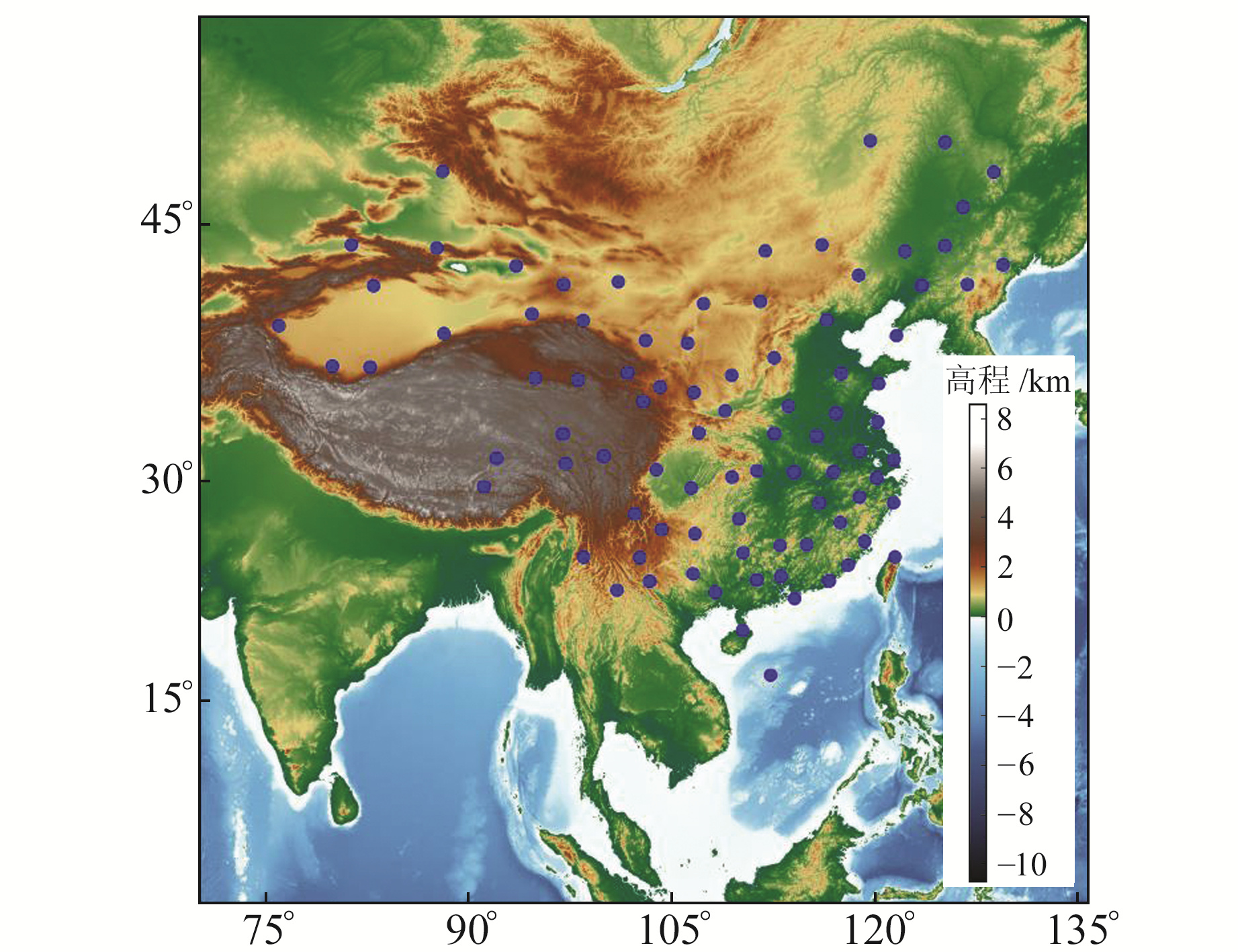
1 数据来源及Tm计算方法 1.1 数据来源选取位于中国区域的88个探空站2015~2017年的数据用于神经网络训练,使用2018年数据进行精度评定。探空站实测数据及位置信息在美国怀俄明州立大学网站下载,可以获得地表温度、相对湿度(relative humidity, RH)、年积日、探空站的经纬度及高程等信息。中国区域探空站分布如图 1所示。
|
图 1 探空站分布 Fig. 1 Distribution of radiosonde stations |
以积分法获得的Tm值精度很高,而探空站只提供地面至不同高度处的气象参数,因此实际计算中常采用离散形式计算Tm,计算方法可参考文献[17],探空站未提供的水汽压值的计算方法可参考文献[18]。
1.2.2 Bevis模型Bevis模型是根据美国中纬度地区的探空数据从统计学上得到的以地表温度为影响因子的线性回归模型,其计算公式如下:
| $ T_m=70.2+0.72 T_s $ | (1) |
GPT系列模型是ECMWF建立的无需实测气象参数的对流层经验模型。目前GPT3模型是该系列中最新、精度最高的模型,可提供全球范围的空间分辨率为1°×1°或5°×5°的Tm、ZTD等多种对流层参数。该模型仅需年积日和测站坐标即可获得测站处Tm值,计算公式可参考文献[7]。
2 中国区域PSOTM模型构建 2.1 BP神经网络基本原理BP神经网络是一种误差逆传播算法训练的前馈神经网络,一般由输入层、隐藏层、输出层构成。其学习过程分为样本的正向传播和误差反向传播2个步骤,具体过程可参考文献[19]。
2.2 PSO原理PSO中每个粒子均代表问题的一组解,初始时所有粒子携带随机初始速度随机分布于搜索空间,并将当下位置记录为个体极值,之后将所有个体极值进行比较得出一个全局最优解,最后更新每个粒子的飞行速度:
| $ \begin{gathered} \boldsymbol{V}_{i n}=\omega \boldsymbol{V}_0+C_1\left(\boldsymbol{P}_{i b}-\boldsymbol{X}_i\right) \text { rand }+ \\ C_2\left(\boldsymbol{G}-\boldsymbol{X}_i\right) \text { rand } \end{gathered} $ | (2) |
式中,Vin为粒子更新后的速度;ω为惯性权重;V0为粒子的初始速度(上一次的速度);C1、C2为学习因子,用以调节粒子受个体最优位置及全局最优位置的影响;rand函数用于生成一个0到1之间的随机数;Pib为第i个粒子搜索的最优位置(个体最优);Xi为粒子的当下位置;G 为全局最优位置。
粒子速度更新后,再根据式(3)更新粒子位置:
| $ \boldsymbol{X}_{i n}=\boldsymbol{X}_i+\boldsymbol{V}_{i n} $ | (3) |
粒子更新完自身速度及位置后,再根据个体最优位置和全局最优位置更新自身速度和位置,直至达到最大迭代次数。
PSO优化BP神经网络的过程中,粒子的位置信息即为BP神经网络各节点的阈值及各层间的连接权值。以BP神经网络输出的误差最小为依据,每个粒子均会得到个体最优解和全局最优解,并以此更新自身位置信息,然后将更新后的位置信息替换BP神经网络中的权值和阈值,并使BP神经网络开始下一次迭代,直至达到PSO的最大迭代次数。
2.3 PSOTM模型构建研究表明,Tm与Ts、es间具有强相关性;纬度(lat)、高程(H)作为空间因素,其变化会影响Tm与Ts间的关系。因此,利用中国区域88个探空站2015~2017年的数据,根据式(4)分析Tm与Ts、es、纬度和高程的相关性,结果如图 2所示。
| $ R=\frac{\sum\limits_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{\sqrt{\sum\limits_{i=1}^n\left(X_i-\bar{X}\right)^2} \sqrt{\sum\limits_{i=1}^n\left(Y_i-\bar{Y}\right)^2}} $ | (4) |

|
图 2 Tm与Ts、es、纬度和高程的相关系数 Fig. 2 Correlation coefficient between Tm and Ts、es, latitude and elevation |
式中,X、Y为不同样本;X、Y为样本的平均值。
由图 2可知,Tm与Tses的皮尔逊系数R分别约为0.92和0.82,相关性强;Tm与纬度、高程的皮尔逊系数R的绝对值在0.3~0.5之间,相关性中等[20]。研究表明,经快速傅里叶变换后,Tm表现出明显的年周期、半年周期。因此,将Ts、es、H、lat信息和探空站采集数据时的年积日(doy)信息作为神经网络的输入,将积分法求得的Tm作为学习目标,建立PSOTM模型,过程如下:
1) 读取输入信息。将探空站2015~2017年Ts、es、H、lat、doy读入数组,并将数据归一化至0~1范围,避免不同量纲的输入数据影响BP神经网络的收敛速度。
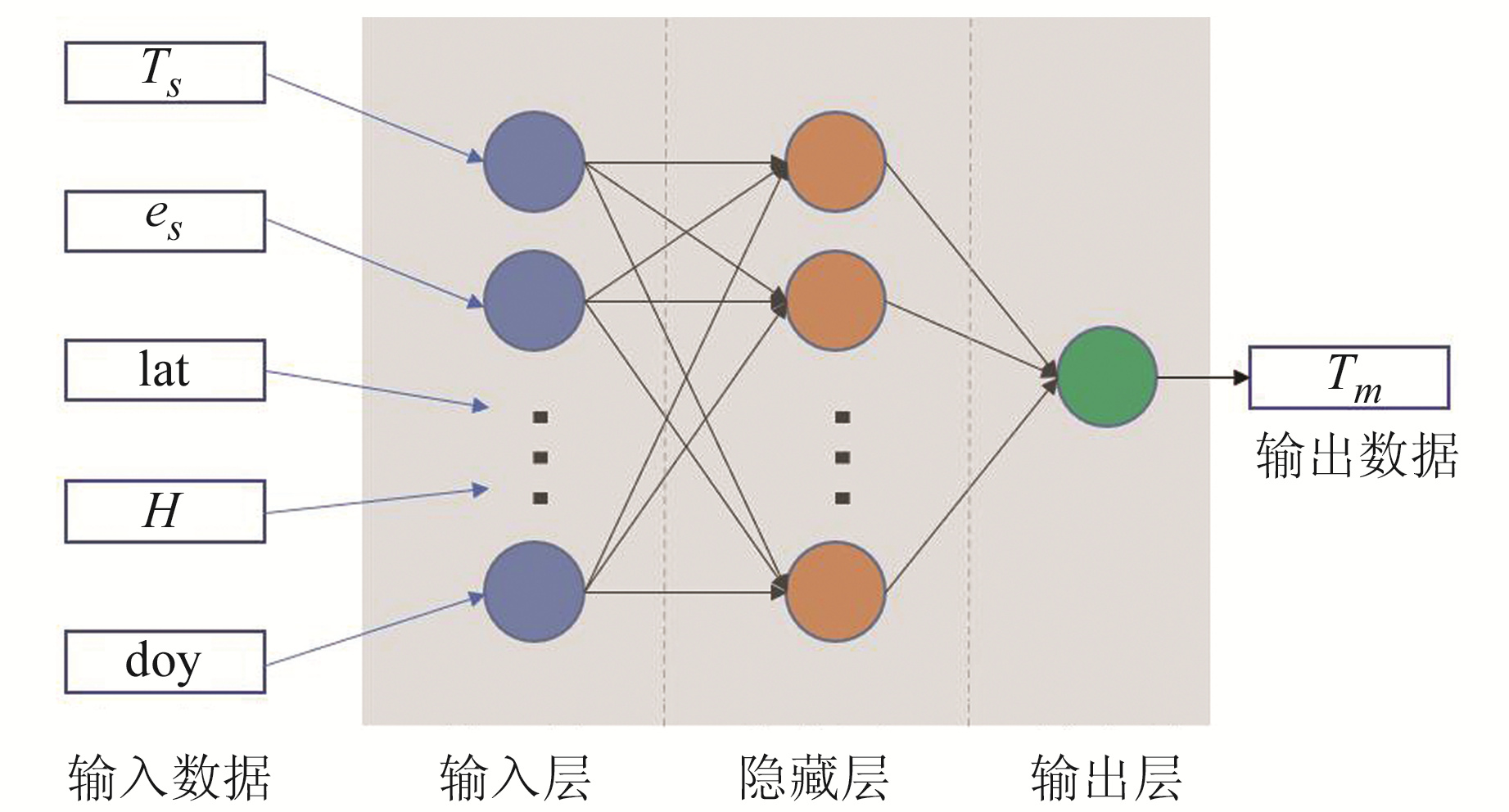
2) 构建BP神经网络。将BP神经网络输入层、隐藏层、输出层的层数均设置为1,输入层节点数设置为5,通过试凑法将隐藏层节点数设置为11,输出层节点数设置为1,最大迭代次数为1 000,训练精度为0.001,学习速率为0.01,输入层与隐藏层的传递函数选为tansig,隐藏层与输出层之间的传递函数选为purelin,训练函数选为trainlm。图 3为本文使用的BP神经网络结构。
|
图 3 BP神经网络结构 Fig. 3 Structure of BP neural network |
3) 初始化PSO参数。为避免粒子数与迭代次数差距过大时算法难以收敛,将粒子数和迭代次数均设置为30。为避免粒子在寻优空间中过于分散、难以收敛,将粒子的个体学习因子C1和群体学习因子C2均设置为2,粒子最大和最小飞行速度设置为0.8和-0.8,惯性权重设为1。为避免PSO迭代后期粒子因自身速度过大而导致收敛至局部最优的情况,每次迭代后将惯性权重减去0.02,使粒子在迭代后期更易收敛至全局最优。参考文献[21-22]在不同情况下选择的PSO参数用以初始化PSOTM模型的PSO参数。较多的粒子数可使初始状态下粒子更均匀地分布于寻优空间,且全局寻优能力强。由于BP神经网络的初始权值、阈值和粒子在寻优空间的初始分布均随机,因此需要充足的迭代次数以保证其收敛。本文实验中,多数情况下粒子群迭代约20次即完成收敛,说明上述参数设置满足迭代需要,可使PSO优化的BP神经网络收敛至全局最优。
4) 算法迭代寻优。迭代完成后,将2018年探空站的Ts、es、H、lat、doy信息输入BP神经网络,输出值反归一化后即为PSOTM模型预测的Tm值。
2.4 GRNN神经网络原理GRNN神经网络是径向基神经网络的一种,由输入层、模式层、求和层、输出层构成,是一种输入信息前向传播的神经网络,具有较强的非线性拟合能力。图 4为本文使用的GRNN神经网络结构。GRNN神经网络的模式层、求和层、输出层对输入向量的计算方式可参考文献[23-24]。

|
图 4 本文使用的GRNN神经网络结构 Fig. 4 Structure of GRNN neural network used in this paper |
为验证PSOTM模型的精度,选取偏差(bias)及均方根误差(RMSE)进行精度评定,具体计算公式如下:
| $ \operatorname{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(y_i^*-y_i\right)^2} $ | (5) |
| $ \text { bias }=\frac{1}{n} \sum\limits_{i=1}^n\left(y_i^*-y_i\right) $ | (6) |
式中,yi*为模型预测值,yi为实测值,n为数据总数量。
为检验PSOTM模型计算中国区域Tm的精度,以中国区域88个探空站2018年的Tm数据为参考值,分别对比Bevis、GPT3、BP神经网络(BPTM)、广义回归神经网络(GRNNTM)、PSOTM模型的RMSE和bias。其中, BPTM与PSOTM模型使用相同结构的神经网络。对训练集进行5折交叉验证,以平均RMSE最小为标准,以0.001为步长,区间设置为0.001~0.05,GRNN神经网络的超参数取0.01。蔡猛等[25]研究指出,GPT3模型计算中国区域Tm时,使用空间分辨率为1°×1°时的计算结果优于使用空间分辨率为5°×5°时的计算结果。为突出PSOTM模型的优越性,选取GPT3模型提供的空间分辨率为1°×1°时的Tm计算结果进行模型间精度对比,结果如表 1所示。
|
|
表 1 几种模型计算Tm的精度对比 Tab. 1 Comparison of Tm calculation accuracy of several models |
由表 1可知:1)从bias来看,Bevis、GPT3、BPTM、GRNNTM、PSOTM模型最大值与最小值之差分别为9.51 K、9.72 K、6.16 K,0.52 K、3.70 K,GRNNTM模型的稳定性相对于其他模型更优。从bias平均值来看,Bevis模型在中国区域表现出较明显的正偏差;GPT3和BPTM模型表现出较明显的负偏差;PSOTM模型的年均bias为0.32 K,较Bevis、GPT3、BPTM模型分别降低68.93%、82.42%、72.41%,但较GRNNTM模型升高37.50%。2)从RMSE来看,Bevis、GPT3、BPTM、GRNNTM、PSOTM模型的年均RMSE分别为4.21 K、4.81 K、3.64 K、3.24 K、3.08 K,PSOTM模型的年均RMSE最小,较Bevis、GPT3、BPTM、GRNNTM模型分别降低26.84%、35.97%、15.38%、4.94%。
为进一步分析PSOTM模型在中国各区域的精度,以2018年探空站的Tm数据为参考值,分别对比4种模型在探空站处的2018年年均RMSE及bias,结果如图 5所示。

|
图 5 不同模型在中国区域的RMSE及bias分布 Fig. 5 RMSE and bias distribution of different models in China region |
由图 5(a)~5(e)可知:1)Bevis模型在中国北部地区表现出正偏差,其值在0~6.45 K之间,西北地区的bias较东北地区更大;GPT3模型同样在中国西北地区表现出较其他区域绝对值更大的负偏差,其值多在-8~-3 K之间。原因为Bevis模型和GPT3模型未考虑高程对Tm的影响,在青藏高原地区适用性不佳。2种模型在中国南部地区均表现出-5~0 K的负偏差。2)BPTM模型在中国大部分地区表现出-4~0 K的负偏差,在云南地区表现出更明显的负偏差,其值约为-5 K;PSOTM模型在中国多数区域偏差为0 K左右,偏差绝对值最大不超过2.5 K;GRNNTM模型在中国区域的bias分布最为均匀,波动最小,bias绝对值的最大值不超过0.5 K,在bias分布及稳定性上较其他模型更优。
由图 5(f)~5(j)可知:1)Bevis模型在中国北部地区的RMSE值多在4~7 K之间,在中国南部地区的RMSE值较小,多在2~4 K之间;GPT3模型在中国北部地区的RMSE值多在4~8 K之间,在中国南部地区的RMSE值多在3~5 K之间。由于未考虑高程的影响,2种模型在青藏高原部分测站处表现出较其他区域更高的RMSE值。2)BPTM模型在黑龙江、宁夏、云南部分站点处表现出4~6 K的RMSE,在其他地区RMSE值多在2~4 K之间;PSOTM模型得益于PSO良好的全局寻优能力,其RMSE分布较BPTM模型更均匀,RMSE值多在2~4 K之间,较BPTM模型波动更小;GRNNTM模型RMSE值多在2~4 K之间,且表现出较高的稳定性。
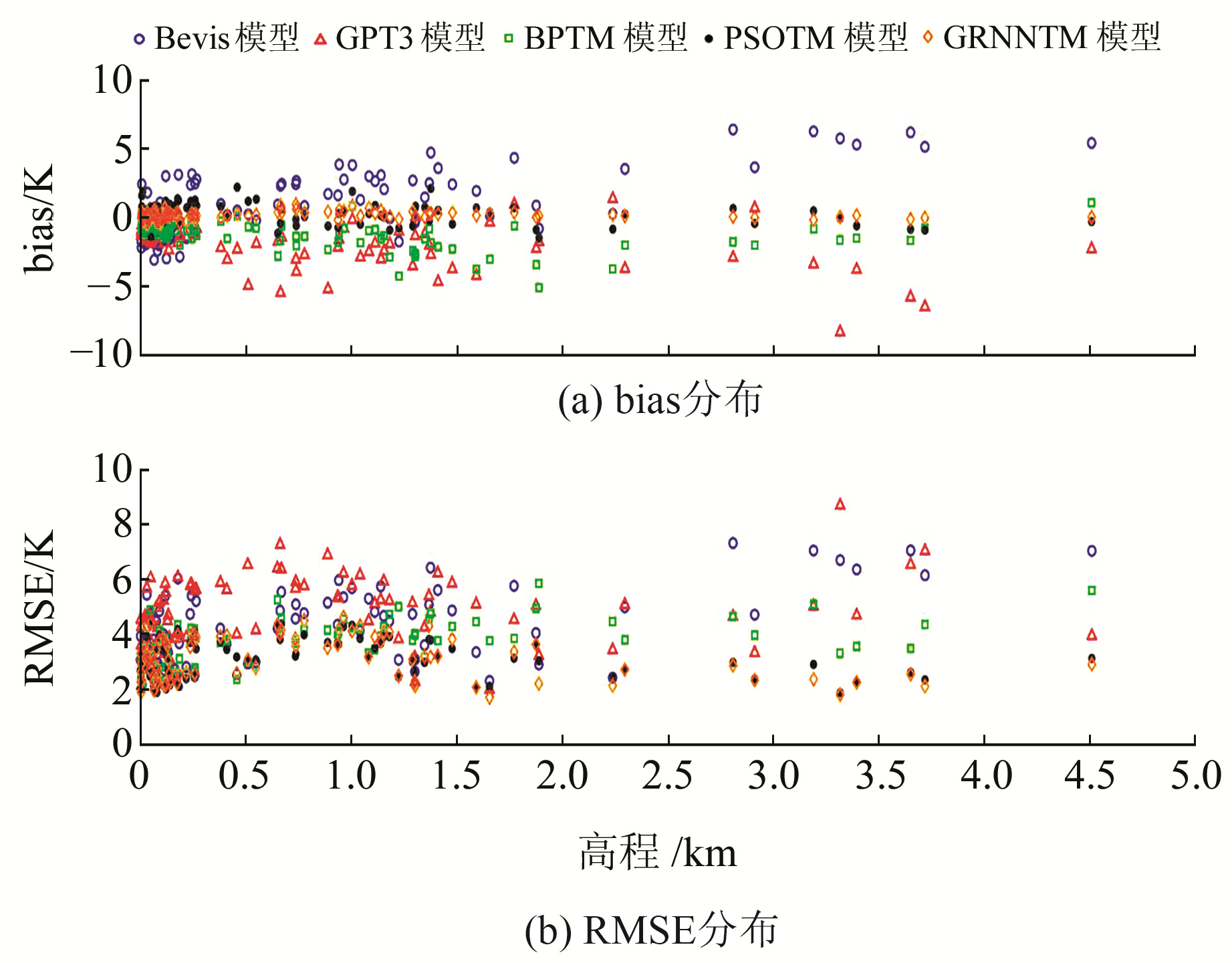
为分析5种模型在纬度和高程上的稳定性,绘制不同模型在纬度和高程上的bias及RMSE变化散点图,结果如图 6、7所示。

|
图 6 不同模型的bias及RMSE随纬度的分布 Fig. 6 Distribution of bias and RMSE of different models with latitudes |
|
图 7 不同模型的bias及RMSE随高程的分布 Fig. 7 Distribution of bias and RMSE of different models with elevations |
由图 6(a)可知:1)纬度低于30°N时,BPTM、GPT3模型在少数测站处表现出约-5 K的bias,在多数测站处bias分布在-3~1 K之间;Bevis模型的bias多分布在-3~3 K之间;PSOTM、GRNNTM模型的bias分布相对更集中,多在-1~1 K之间。2)随着纬度增高,Bevis模型表现出较明显的正偏差,其值主要在2~7 K之间;GPT3模型表现出较明显的负偏差,其值多在-5~0 K之间。在30°~45°N时,Bevis和GPT3模型在部分测站处bias的绝对值大于5 K,说明这2种模型在计算相应地区Tm时易发生波动。BPTM模型的bias多分布在-2~0 K之间,PSOTM与GRNNTM模型的bias多集中于-1~1 K之间。
由图 6(b)可知,5种模型的年均RMSE值均随纬度的增高而增大,PSOTM与GRNNTM模型的增大趋势低于其他3种模型,且RMSE值在纬度上的分布更为集中、波动幅度更小,说明在中国区域内PSOTM和GRNNTM模型在纬度上的精度和稳定性优于其他3种模型。
由图 7(a)可知:1)高程低于2.5 km时,Bevis模型的bias多分布在-4~5 K之间;GPT3和BPTM模型的bias多分布在-5~0 K之间;PSOTM和GRNNTM模型的bias多在0 K处波动。2)随着高程的增加,由于Bevis和GPT3模型并未考虑高程的影响,2种模型分别表现出更加明显的正偏差和负偏差,其值分别在5 K和-5 K处波动;而BPTM、PSOTM和GRNNTM模型的bias多分布在-2~1 K之间,且PSOTM和GRNNTM模型的bias分布相对BPTM模型更集中在0 K处。
由图 7(b)可知,高程低于2.5 km时,Bevis和GPT3模型的RMSE多分布在4~6 K之间;BPTM模型的RMSE多分布在2~6 K之间;PSOTM和GRNN模型的RMSE多分布在2~4 K之间。随着高程的增加,Bevis模型的RMSE值多分布在6~8 K之间;GPT3模型的RMSE值多分布在3~9 K之间;BPTM模型的RMSE多分布在3~5 K之间;PSOTM和GRNNTM模型的RMSE值随高程的分布更均匀,且数值均在4 K以下,较其他3种模型具有更高的精度。
综上,在计算中国区域Tm时,PSOTM模型相较于Bevis、GPT3和BPTM模型具有更高的精度,其在不同纬度、高程上的RMSE和bias小于其他3种模型,在中国区域具有更好的稳定性和适用性。相较于GRNNTM模型,PSOTM模型的年均bias略大,年均RMSE略小。由此可知,PSO具有优秀的全局寻优能力,用PSO优化的BP神经网络计算中国区域Tm具有可行性。
4 结语Tm是反演PWV的关键参量之一,目前常用的Tm模型由于顾及因素相对较少、对Tm周期性描述不够全面等原因,在中国区域精度欠佳。本文以BP神经网络算法为基础,使用PSO优化BP神经网络的连接权值和节点阈值,使其在不同参数间具有优秀的非线性拟合能力,可在一定程度上克服全局寻优性较差的缺点。通过实际算例,本文验证了所提的PSOTM模型计算中国区域Tm的可行性,可为使用机器学习方法建立Tm模型、计算中国区域Tm和检测大气水汽提供参考。
中国区域经纬度及高程跨度大、气候多样,Tm与其影响因子间函数关系复杂,而PSOTM模型表现出良好的精度,说明该算法拟合能力较强,具有应用于其他区域或计算全球范围Tm的潜力。下一步将使用不同区域的数据源对PSOTM模型进行网络训练并验证其适应性。
| [1] |
盛裴轩, 毛节泰, 李建国, 等. 大气物理学[M]. 北京: 北京大学出版社, 2013 (Sheng Peixuan, Mao Jietai, Li Jianguo, et al. Atmospheric Physics[M]. Beijing: Peking University Press, 2013)
(  0) 0) |
| [2] |
姚宜斌, 张顺, 孔建. GNSS空间环境学研究进展和展望[J]. 测绘学报, 2017, 46(10): 1 408-1 420 (Yao Yibin, Zhang Shun, Kong Jian. Research Progress and Prospect of GNSS Space Environment Science[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 408-1 420)
(  0) 0) |
| [3] |
Emardson T R, Derks H J P. On the Relation between the Wet Delay and the Integrated Precipitable Water Vapour in the European Atmosphere[J]. Meteorological Applications, 2000, 7(1): 61-68 DOI:10.1017/S1350482700001377
(  0) 0) |
| [4] |
Böhm J, Heinkelmann R, Schuh H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683 DOI:10.1007/s00190-007-0135-3
(  0) 0) |
| [5] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1 069-1 073 DOI:10.1002/grl.50288
(  0) 0) |
| [6] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere(GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [7] |
Landskron D, Böhm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
(  0) 0) |
| [8] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research, 1992, 97(D14): 15 787-15 801 DOI:10.1029/92JD01517
(  0) 0) |
| [9] |
于胜杰, 柳林涛. 水汽加权平均温度回归公式的验证与分析[J]. 武汉大学学报: 信息科学版, 2009, 34(6): 741-744 (Yu Shengjie, Liu Lintao. Validation and Analysis of the Water-Vapor-Weighted Mean Temperature from Tm-Ts Relationship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 741-744)
(  0) 0) |
| [10] |
Yao Y B, Zhang B, Xu C Q, et al. Improved One/Multi-Parameter Models that Consider Seasonal and Geographic Variations for Estimating Weighted Mean Temperature in Ground-Based GPS Meteorology[J]. Journal of Geodesy, 2014, 88(3): 273-282 DOI:10.1007/s00190-013-0684-6
(  0) 0) |
| [11] |
Yao Y B, Zhang B, Xu C Q, et al. Analysis of the Global Tm-Ts Correlation and Establishment of the Latitude-Related Linear Model[J]. Chinese Science Bulletin, 2014, 59(19): 2 340-2 347 DOI:10.1007/s11434-014-0275-9
(  0) 0) |
| [12] |
姚宜斌, 孙章宇, 许超钤. Bevis公式在不同高度面的适用性以及基于近地大气温度的全球加权平均温度模型[J]. 测绘学报, 2019, 48(3): 276-285 (Yao Yibin, Sun Zhangyu, Xu Chaoqian. Applicability of Bevis Formula at Different Height Level and Global Weighted Mean Temperature Model Based on Near-Earth Atmospheric Temperature[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(3): 276-285)
(  0) 0) |
| [13] |
姚宜斌, 刘劲宏, 张豹, 等. 地表温度与加权平均温度的非线性关系[J]. 武汉大学学报: 信息科学版, 2015, 40(1): 112-116 (Yao Yibin, Liu Jinhong, Zhang Bao, et al. Nonlinear Relationships between the Surface Temperature and the Weighted Mean Temperature[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 112-116)
(  0) 0) |
| [14] |
Ding M H. A Neural Network Model for Predicting Weighted Mean Temperature[J]. Journal of Geodesy, 2018, 92(10): 1 187-1 198 DOI:10.1007/s00190-018-1114-6
(  0) 0) |
| [15] |
Sun Z Y, Zhang B, Yao Y B. Improving the Estimation of Weighted Mean Temperature in China Using Machine Learning Methods[J]. Remote Sensing, 2021, 13(5)
(  0) 0) |
| [16] |
Kennedy J, Eberhart R. Particle Swarm Optimization[C]. Proceedings of ICNN'95-International Conference on Neural Networks, Perth, 1995
(  0) 0) |
| [17] |
李浩杰, 刘立龙, 黄良珂, 等. 顾及多因子影响的中国区域Tm模型精化研究[J]. 大地测量与地球动力学, 2022, 42(4): 393-397 (Li Haojie, Liu Lilong, Huang Liangke, et al. Refinement of Tm Model Considering the Influence of Multi-Factors in China Region[J]. Journal of Geodesy and Geodynamics, 2022, 42(4): 393-397)
(  0) 0) |
| [18] |
Li H J, Li J Y, Liu L L, et al. Random Forest-Based Model for Estimating Weighted Mean Temperature in China's Mainland[J]. Atmosphere, 2022, 13(9): 1 368-1 382 DOI:10.3390/atmos13091368
(  0) 0) |
| [19] |
王勇, 张立辉, 杨晶. 基于BP神经网络的对流层延迟预测研究[J]. 大地测量与地球动力学, 2011, 31(3): 134-137 (Wang Yong, Zhang Lihui, Yang Jing. Study on Prediction of Zenith Tropospheric Delay by Use of BP Neural Network[J]. Journal of Geodesy and Geodynamics, 2011, 31(3): 134-137)
(  0) 0) |
| [20] |
陈锦超, 董雪玲, 张婉, 等. 北京市霾天PM2.5污染特征及其与气象因素的关系[J]. 环境科学与技术, 2018, 41(8): 87-94 (Chen Jinchao, Dong Xueling, Zhang Wan, et al. Characteristics of PM2.5 in Haze Days in Beijing and Its Relationship with Meteorological Factors[J]. Environmental Science and Technology, 2018, 41(8): 87-94)
(  0) 0) |
| [21] |
王颖颖, 庄毅, 孙逸帆. 基于粒子群优化BP神经网络的可靠性评估模型[J]. 计算机与现代化, 2022(12): 42-49 (Wang Yingying, Zhuang Yi, Sun Yifan. Reliability Evaluation Model of BP Neural Network Based on Particle Swarm Optimization[J]. Computer and Modernization, 2022(12): 42-49)
(  0) 0) |
| [22] |
付睿. 基于改进粒子群优化的LSTM模型在股票价格预测中的应用[D]. 济南: 山东大学, 2022 (Fu Rui. Application of LSTM Model Based on Improved Particle Swarm Optimization in Stock Price Prediction[D]. Ji'nan: Shandong University, 2022)
(  0) 0) |
| [23] |
Specht D F. A General Regression Neural Network[J]. IEEE Transactions on Neural Networks, 1991, 2(6): 568-576 DOI:10.1109/72.97934
(  0) 0) |
| [24] |
张肃. 基于机器学习的高速光信号光性能监测[D]. 北京: 北京交通大学, 2018 (Zhang Su. Optical Performance Monitoring of High Speed Optical Signal Based on Machine Learning[D]. Beijing: Beijing Jiaotong University, 2018)
(  0) 0) |
| [25] |
蔡猛, 刘立龙, 黄良珂, 等. GPT3模型反演GNSS大气可降水量精度评定[J]. 大地测量与地球动力学, 2022, 42(5): 483-488 (Cai Meng, Liu Lilong, Huang Liangke, et al. Evaluation of GNSS Precipitable Water Vapor Derived from GPT3 Model[J]. Journal of Geodesy and Geodynamics, 2022, 42(5): 483-488)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


