2. 山东省地质测绘院,济南市二环东路11101号,250014
受区域地质构造活动、矿区和城市地下水开采等多种因素的影响,引黄济青沿线干渠的渠堤及堤岸基础存在不同程度的地表形变区。传统监测地表形变的方法如水准测量、GPS等作业效率低、劳动强度大,只能获得个别点的地表形变信息,难以精确获得区域整体的形变分布特征[1]。InSAR及其改进技术具有高空间分辨率、范围广、全天候、全天时观测等优势,已成为地表形变监测领域的一种新的空间对地观测方法[2-4]。
目前,基于InSAR技术对引黄济青沿线地表形变进行监测的研究较少,没有宏观上获取的引黄济青沿线地表形变的位置、时空分布与演变过程的信息。基于此,本文首先利用时序SBAS-InSAR技术处理覆盖研究区的38景Sentinel-1 SAR影像数据,获得2019-02~2021-10引黄济青沿线的年平均形变速率、各成像时刻的累积地表形变量、最终累积地表形变量等信息,提取特征点的地表形变时间序列,并结合实际情况对沿线地表形变的时空演化特征进行分析;然后,在地表形变明显区域进行缓冲区处理,提取剖面线上高相干像元的地表形变值,并计算其形变梯度,分析引黄济青干渠的稳定性;最后,利用Prophet模型对特征点的地表形变进行预测分析,并对模型预测的精确度和可靠性进行验证。
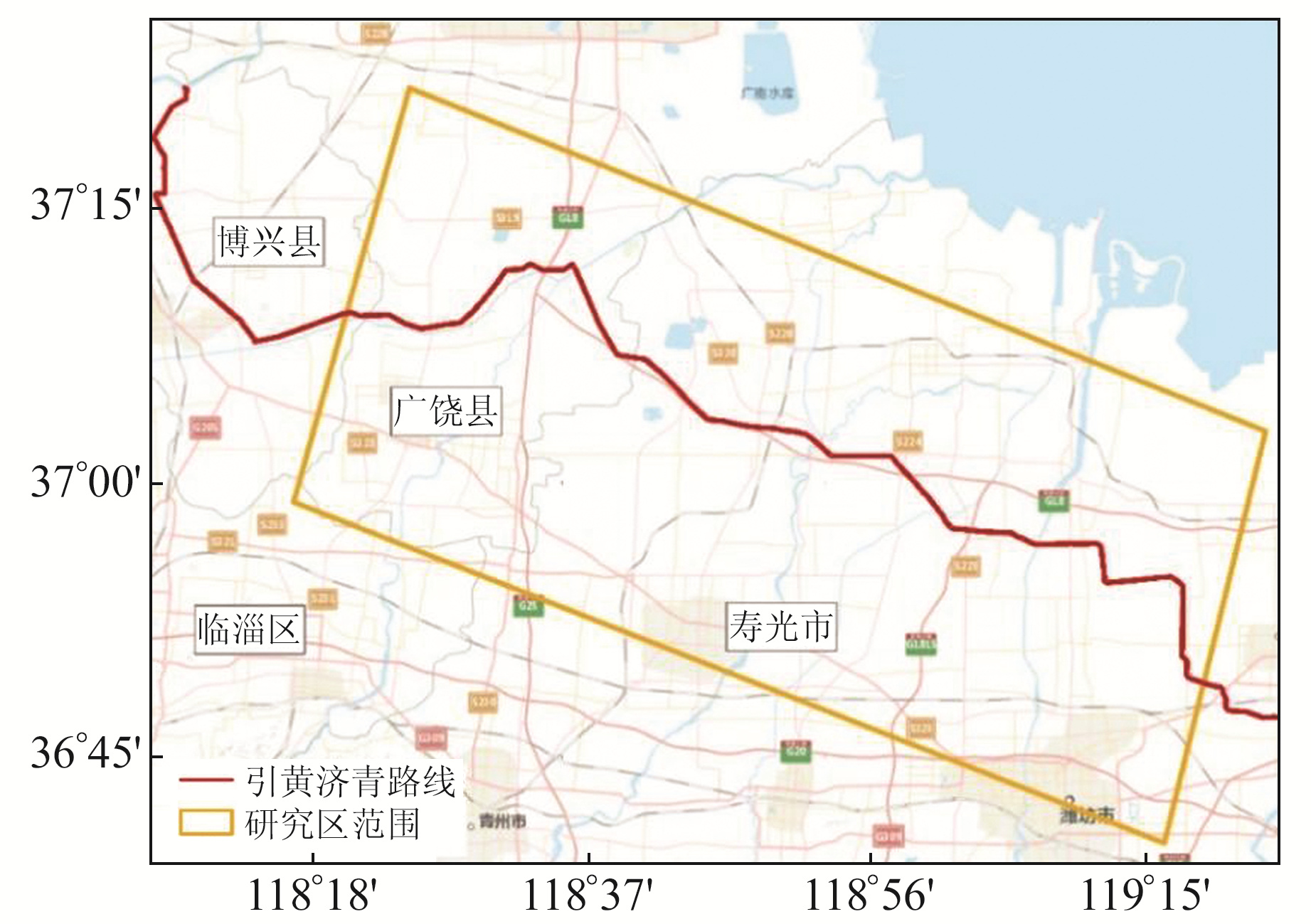
1 研究区及数据来源 1.1 研究区概况引黄济青工程位于山东省中部,起点位于博兴县沉沙池出口,途经滨州、东营、潍坊、青岛,最终引入青岛即墨棘洪滩水库,全长291.14 km,是一项长距离、跨流域的大型供水工程。本文研究区为引黄济青路线中段(图 1矩形框)。
|
图 1 研究区示意图 Fig. 1 Sketch map of study area |
选取覆盖研究区的38景Sentinel-1 SAR影像,时间跨度为2019-02-16~2021-10-03,影像极化方式为VV,波段为C波段。
此外,收集NASA提供的30 m的SRTM DEM高程数据和精密轨道数据,分别用于消除地形相位引起的误差和轨道误差对形变监测结果的影响。
2 原理与方法 2.1 SBAS-InSAR原理假设已获取时间依次为t0, …, ti, …, tN的N+1幅SAR影像数据,设定空间基线和时间基线阈值进行差分干涉,获得M幅差分干涉图,M满足的条件为:
| $ \frac{N+1}{2} \leqslant M \leqslant N\left(\frac{N+1}{2}\right) $ | (1) |
假设所有的差分干涉图都经过正确的相位解缠,且解缠后的相位均被校正到某个形变趋势稳定或者形变信息已知的高相干点像元上。记时刻ti(i=1, …, N)相对于初始时刻t0的差分干涉相位为φ (ti),φ (ti)为未知参数,通过数据处理得到的差分干涉相位记为δ φ (tk)(k=1, …, M),则有2个时间序列:
| $ \boldsymbol{\varphi}\left(t_i\right)=\left[\varphi\left(t_1\right), \cdots, \varphi\left(t_N\right)\right]^{\mathrm{T}} $ | (2) |
| $ \delta \boldsymbol{\varphi}\left(t_k\right)=\left[\delta \varphi\left(t_i\right), \cdots, \delta \varphi\left(t_M\right)\right]^{\mathrm{T}} $ | (3) |
对于第k(k=1, …, M)幅差分干涉图中的任一像元(x, r)有:
| $ \begin{gathered} \Delta \varphi_k(x, r)=\varphi\left(t_B, x, r\right)-\varphi\left(t_A, x, r\right) \approx \\ \frac{4 \pi}{\lambda}\left[d\left(t_B, x, r\right)-d\left(t_A, x, r\right)\right] \end{gathered} $ | (4) |
式中,λ为雷达波长,tA和tB分别为第k幅差分干涉图对应的主、从影像的获取时刻,d(tA, x, r)和d(tB, x, r)分别为tA和tB时刻像元(x, r)相对于初始时刻t0在LOS方向上的累积量形变。其中的φ(tA, x, r)可写为:
| $ \begin{gathered} \varphi\left(t_A, x, r\right)=\frac{4 \pi}{\lambda}\left[d\left(t_A, x, r\right)-\right. \\ \left.d\left(t_0, x, r\right)\right]=\frac{4 \pi}{\lambda} d\left(t_A, x, r\right) \end{gathered} $ | (5) |
对任一像元,可以列出线性形变模型:
| $ \boldsymbol{A} \boldsymbol{\varphi}=\delta \mathit{Φ} $ | (6) |
式中,A是一个M×N维矩阵,可以直接由已知的差分干涉图得到。
在实际情况中,N+1景SAR影像通常会被划分到若干个短基线集中(即L≥2),此时,矩阵A的秩为N-L+1,即A T A是个奇异矩阵,因此式(6)有无穷多个解。SBAS-InSAR采用奇异值分解方法将多个基线集联合,求其最小范数最小二乘解。
2.2 地表形变梯度引黄济青工程作为山东省的重点工程之一,其稳定性至关重要。本文使用形变梯度来描述引黄济青工程地表形变在不同方向上的形变速率,可以展现出地表形变的不均匀性[5-6],而不均匀地表形变所带来的危害高于均匀形变带来的危害[7-8]。
在引黄济青沿线等间距选取高相干像元,提取高相干像元的形变信息,计算2个高相干像元之间的形变梯度,即
| $ K_{z, z+1}=\frac{\Delta h}{s}=\frac{x_{z+1}-x_z}{s} $ | (7) |
式中,Kz, z+1是第z个和第z+1个像元之间的地表形变梯度,xz+1、xz分别为第z个和第z+1个像元的地表形变值,s为第z个和第z+1像元之间的距离。
2.3 Prophet模型Prophet模型是一种结合时间序列分解和机器学习拟合的时序模型,其在建模过程中考虑了趋势性、节假日效应、周期性以及外部变量等因素的影响,预测效果较好,相对于传统时间序列模型有明显优势[9]。
Prophet模型可以表示为:
| $ y(t)=g(t)+s(t)+h(t)+\varepsilon_t $ | (8) |
式中,g(t)为趋势项,表示时间序列非周期的变化趋势,s(t)为周期项,表示时间序列中呈现周期性变化的部分,h(t)为节假日项,表示时间序列中那些潜在的具有非固定周期的节假日对预测值造成的影响,εt为误差项,服从高斯分布。
基于逻辑回归函数来模拟趋势项:
| $ \begin{gathered} g(t)= \\ \frac{C(t)}{1+\exp \left(-\left(k+\boldsymbol{a}(t)^{\mathrm{T}} \boldsymbol{\delta}\right)\left(t-\left(m+\boldsymbol{a}(t)^{\mathrm{T}} \boldsymbol{\gamma}\right)\right)\right)} \end{gathered} $ | (9) |
式中,a (t)=[a1(t), a2(t), …, as(t)],δ =[δ1, δ2, …, δs]T,γ =[γ1, γ2, …, γs]T,C(t)为承载量,k为增长率,m为偏移量。
使用傅里叶级数来模拟时间序列的周期性,假设P表示时间序列的周期,则傅里叶级数的形式为:
| $ \begin{gathered} s(t)=\sum\limits_{n=1}^N\left(a_n \cos \left(\frac{2 \pi n t}{P}\right)+\right. \\ \left.b_n \sin \left(\frac{2 \pi n t}{P}\right)\right)=x(t) \boldsymbol{\beta} \end{gathered} $ | (10) |
式中,β =[a1, b1, a2, b2, …, aN, bN],为Prophet模型的初始化参数,其初始化参数β ~N(0,σ2),σ越大,表示季节效应越明显,σ越小,表示季节效应越不明显。
假设有L个节假日,那么节假日效应模型为:
| $ h(t)=\boldsymbol{Z}(t) \boldsymbol{k}=\sum\limits_{i=1}^L k_i \cdot 1_{\left\{t \in D_i\right\}} $ | (11) |
式中,Z (t)=[1{t∈Di}, …, 1{t∈DL}],k =[k1, …, kL]T。
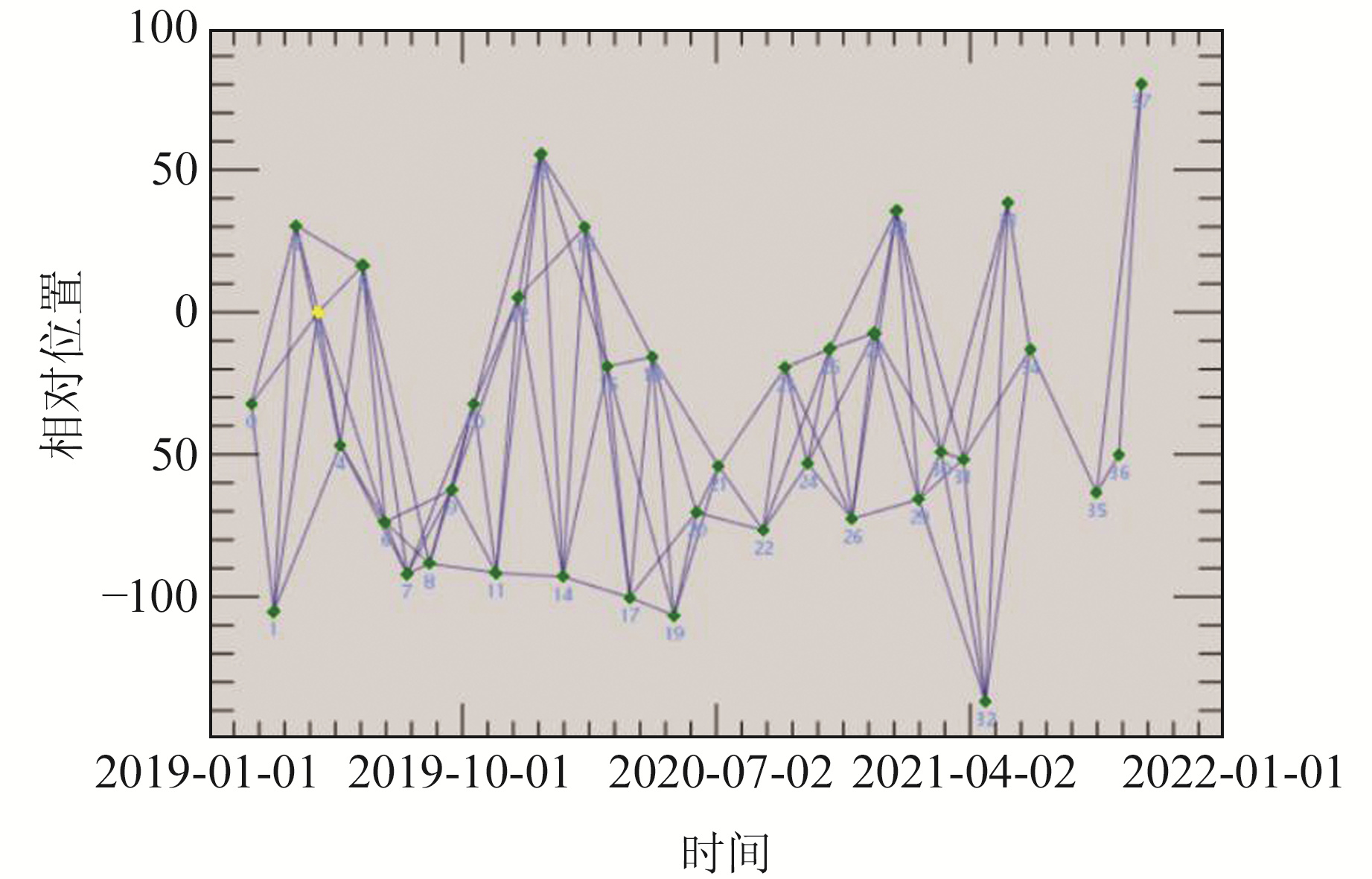
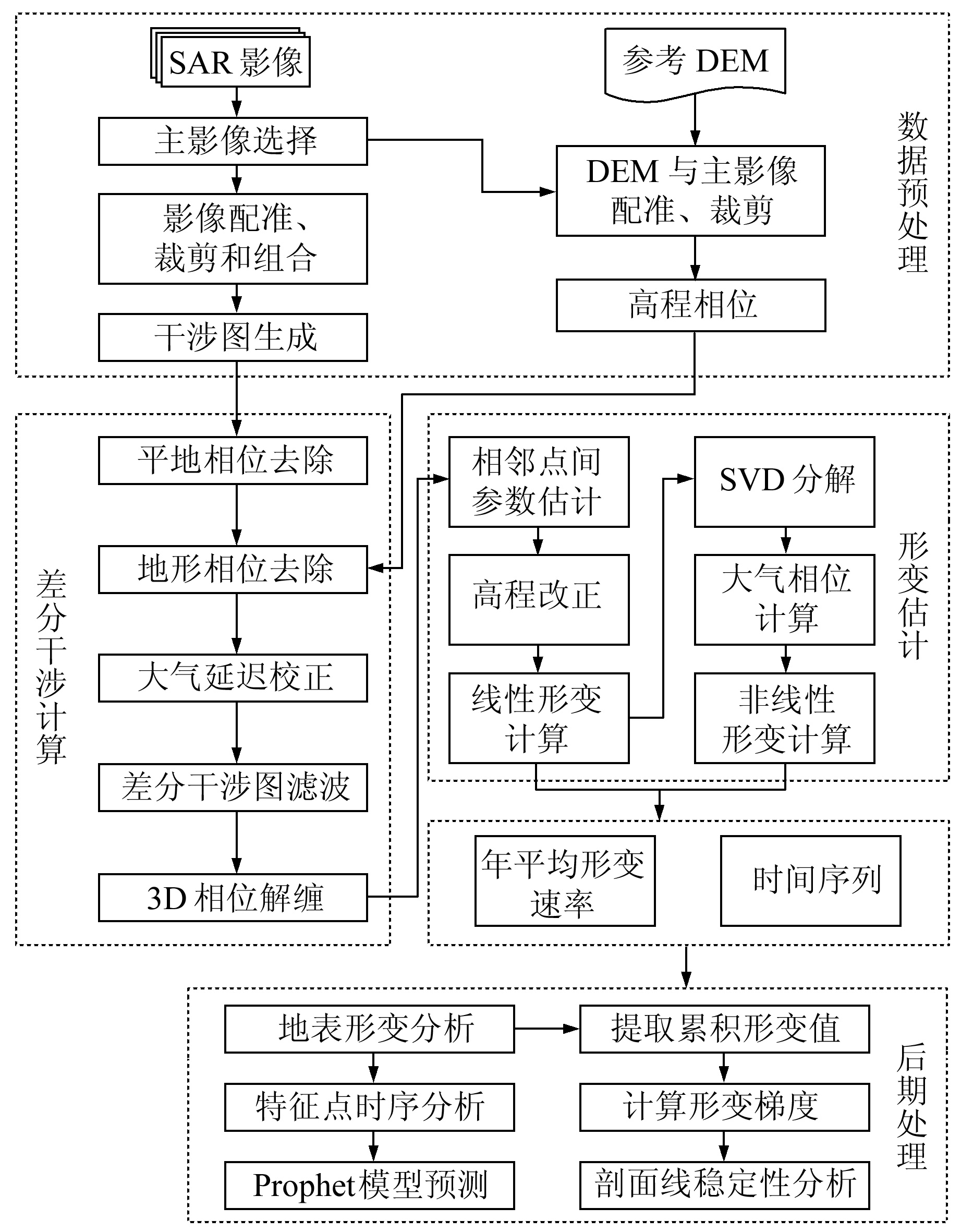
2.4 数据处理流程使用GAMMA软件[10]处理SAR影像。根据综合相干系数最小的原则[11],选取一景影像作为主影像,其余N景SAR影像作为从影像与主影像进行配准。对配准好的影像进行去斜、裁剪等处理;设置时空基线阈值,生成100个干涉像对,处理得到时空基线分布图(图 2)。设置距离向和方位向为4 ∶1的多视处理来抑制噪声,与已有DEM数据进行差分干涉处理;使用Goldstein滤波方法对各差分干涉图进行滤波处理,得到M幅滤波增强后的时序差分干涉图。使用最小费用流法(minimum cost flow, MCF)对滤波增强后的各差分干涉图进行相位解缠,对SBAS-InSAR的结果进行后续处理,得到研究区形变信息。基于形变梯度对引黄济青沿线地表的稳定性进行分析,然后利用Prophet模型对沿线若干特征点的地表形变进行预测。图 3给出了主要的数据处理流程与方法。
|
图 2 时空基线分布 Fig. 2 Spatiotemporal baseline distribution |
|
图 3 SBAS-InSAR数据处理流程 Fig. 3 SBAS-InSAR data processing flow chart |
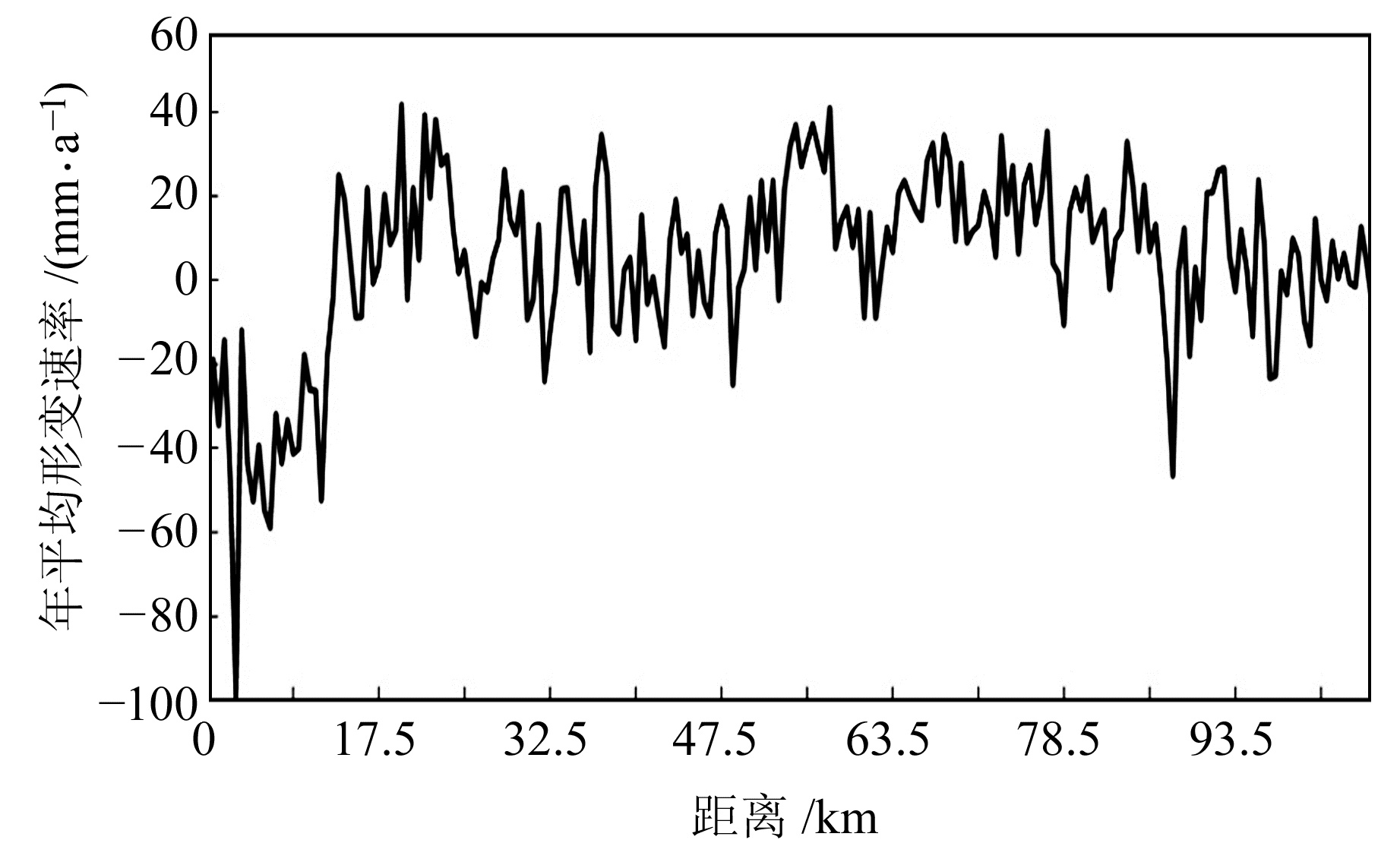
计算获取2019-02-16~2021-10-03的地表形变信息,图 4为年平均形变速率图,形变速率为负值表示地面沉降,正值表示地面抬升。图 5为引黄济青沿线地表形变折线图,横坐标为从起始点到形变点的距离(以研究区左侧为起始点)。

|
图 4 引黄济青区域年平均形变速率 Fig. 4 Annual average deformation rate of the Yellow river to Qingdao diversion region |
|
图 5 引黄济青沿线地表形变速率折线图 Fig. 5 Line chart of surface deformation rate along the Yellow river to Qingdao diversion route |
从图 4可以看出,大部分区域年平均形变速率为正值,表现为地表抬升;稻庄镇、大码头镇、大王镇、营里镇、羊口镇、稻田镇等区域形变速率为负值,表现为地表沉降,沉降速率多在-60~0 mm/a之间,沉降最严重的广饶县最大形变速率达到-167 mm/a。从图 5看出,引黄济青沿线的形变速率主要在-60~40 mm/a之间,形变速率波动与年平均形变速率图形变区域较吻合。
造成引黄济青沿线地表形变的因素可能包括城市地面沉降、开采沉陷、人类工程活动和数据处理误差等。从图 4可以看出,地表形变集中在广饶县境内。查阅资料可知,造成广饶县地表形变的主要因素为地下水超采、城市建设等。中深层地下水长期超采形成地下水降落漏斗,加上城市建设,特别是高层建筑的兴建,对其下部地层持续加载,造成上部松散地层固结压缩,引起大范围的地面沉降,进而对引黄济青沿线造成影响。
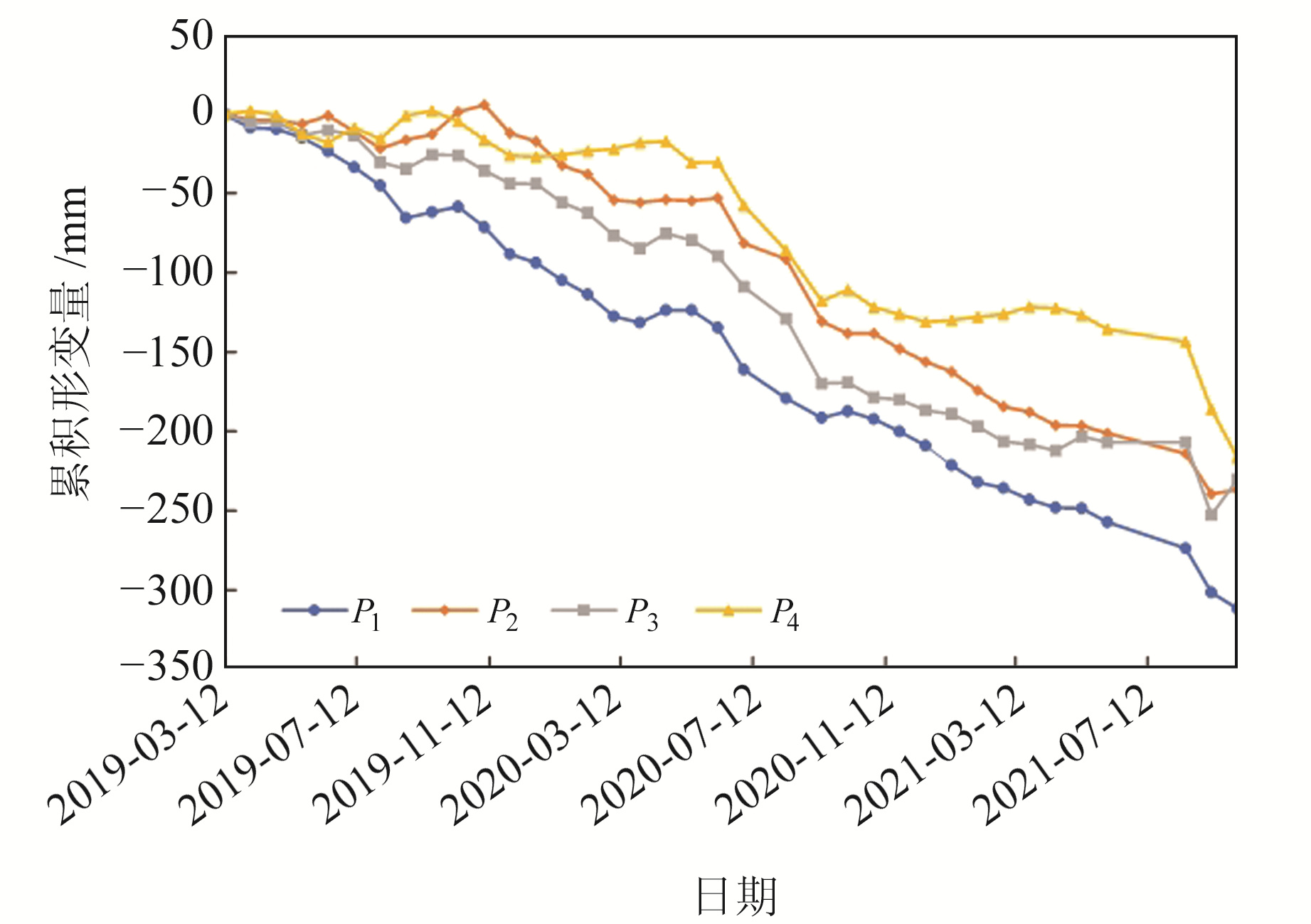
在沉降中心选取4个特征点P1、P2、P3、P4(图 4),提取其地表形变时间序列,结果见图 6,其中,P1、P2、P3位于广饶县境内,P4位于寿光市营里镇。
|
图 6 特征点累积形变时序折线图 Fig. 6 Line chart of cumulative deformation time series of feature points |
从图 6可以看出,各个特征点累积形变量基本处于持续沉降趋势,沉降曲线波动较小,趋势相似,表现出较强的线性特征。至2021-10-03四个特征点累积形变值分别达到-320 mm、-239 mm、-238 mm和-212 mm,其中,P1点形变量明显大于其他3点,其地理位置在广饶县城区。广饶县地下水长期处于超采状态,形成地下水降落漏斗,造成该区域出现地表沉降,代表区域包括广饶县城区、稻庄镇和大王镇等。
3.2 引黄济青沿线地表形变稳定性分析根据图 4,在地表形变明显区域内对引黄济青沿线2 km范围进行缓冲区处理,获得如图 7所示的缓冲区累积形变图,其中,a、c为纵向剖面线,b、d为横向剖面线。分别获取横纵剖面线累积形变值,以此为依据计算剖面线的形变梯度,结果见8,其中,图 8(a)为剖面线累积形变量,8(b)为剖面线形变梯度。

|
图 7 2 km缓冲区累积沉降图 Fig. 7 Cumulative settlement map of 2 km buffer zone |

|
图 8 累积形变值及形变梯度折线图 Fig. 8 Line chart of cumulative deformation value and deformation gradient |
对比分析图 8(a)、8(b)可以看出,剖面线a出现一次形变梯度值的骤升,与形变严重区域相吻合,剖面线c形变梯度值比较稳定;横向剖面线b、d各像元点之间存在较大的沉降波动,相应的形变梯度值变化也较大,整体上地表形变严重区域和形变梯度较大区域有较大的重叠。由此可知,纵向剖面线的地表形变速率较稳定,不均匀形变较少;横向剖面线存在较多的不均匀形变,可能是由引黄济青沿线周围的地质活动引起的,应多加关注。
引黄济青沿线横纵剖面线形变梯度稳定性分析表明,引黄济青沿线整体处于一个比较稳定的状态。
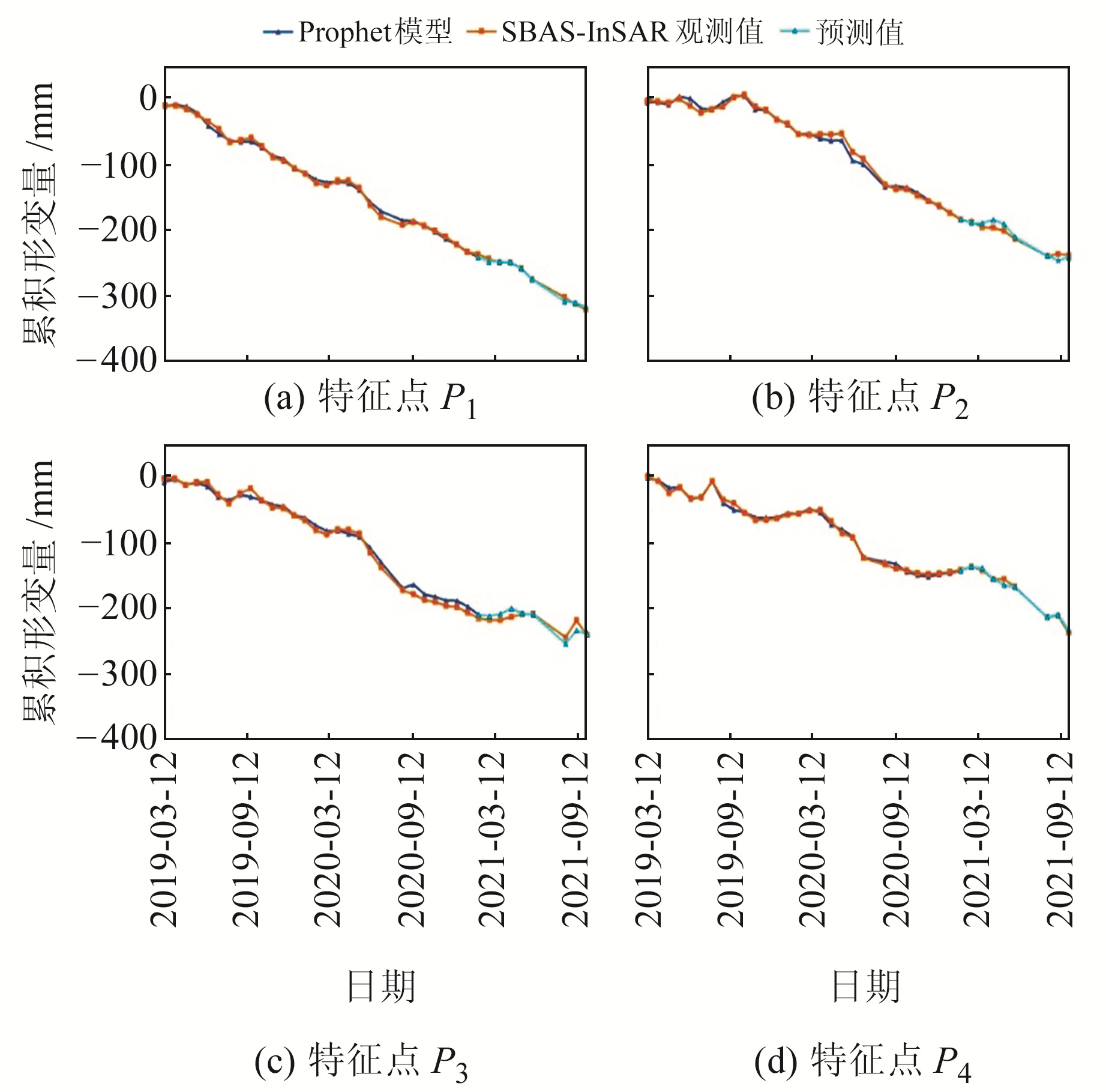
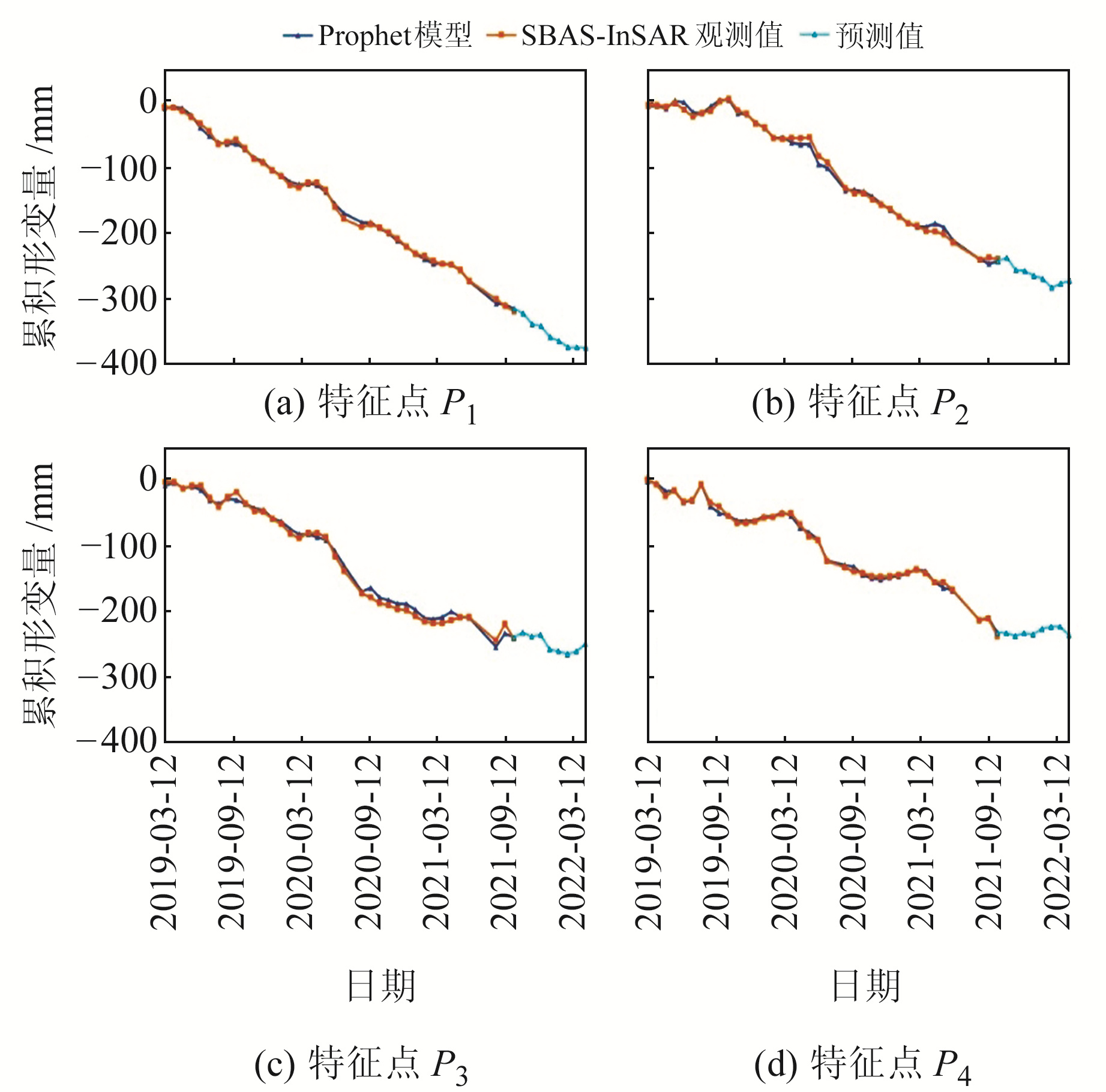
3.3 基于Prophet模型的引黄济青地表形变预测Prophet模型可以根据已知的时间序列模型预测未来时间序列的走向。以地表形变较为严重的P1、P2、P3、P4点前30期数据作为训练样本,对后8期以及未来8期地表形变进行预测,结果分别见图 9、10。
|
图 9 SBAS-InSAR观测值与后8期Prophet模型预测值对比 Fig. 9 Comparison between SBAS-InSAR observation values and predicted values of Prophet model in the last 8 periods |
|
图 10 SBAS-InSAR观测值与未来8期Prophet模型预测值对比 Fig. 10 Comparison between SBAS-InSAR observation values and predicted values of Prophet model in the future 8 periods |
从图 9中可以看出,4个特征点后8期数据的预测值与SBAS观测值均具有较好的一致性,P1点预测结果与观测值最吻合;P2、P3点预测值与观测值之间差异相对大一些,但误差值均小于15 mm;P4点预测结果与观测值存在一些差异,但整体沉降趋势一致。
从图 10看出,P1点沉降值逐步增加,沉降趋势接近指数函数形式,到2022-04沉降值达到-375 mm;P2~P4点训练样本具有一定的周期波动性,预测数值同样存在波动,沉降值不是单纯的增加,其中,P2点出现2次小幅抬升,沉降值较2021-10增加30 mm,P3、P4点形变值上下波动,总体沉降值变化不大,分别增加10 mm和4 mm。
综上,Prophet模型能够在数据量和地表形变量较小时进行较好的模拟和预测。
4 结语本文利用SBAS-InSAR技术对2019-02-16~2021-10-03覆盖引黄济青沿线的38景Sentinel-1数据进行处理,获得研究区大范围、长时间的地表形变信息;基于地表形变结果,针对沉降严重区域进行稳定性分析,并利用Prophet模型预测特征点未来的形变趋势,得到结论如下:
1) 研究区域内大部分地区地表形变速率和累积形变量都较小,处于稳定状态;大部分区域形变速率位于-60~40 mm/a之间,主要表现为地面抬升;沉降区主要分布在广饶县等地方,最大沉降速率达到-167 mm/a,最大累积沉降值为-366 mm。
2) 地表形变严重区域与形变梯度较大区域高度重合,并且横向剖面线形变梯度变化大于纵向剖面线,应给予更多关注。
3) Prophet模型在数据量和形变量较小的情况下预测效果较好。
| [1] |
侯安业, 张景发, 刘斌, 等. PS-InSAR与SBAS-InSAR监测地表沉降的比较研究[J]. 大地测量与地球动力学, 2012, 32(4): 125-128 (Hou Anye, Zhang Jingfa, Liu Bin, et al. Comparative Study on Monitoring Surface Subsidence with PS-InSAR and SBAS-InSAR[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 125-128)
(  0) 0) |
| [2] |
晏霞, 刘媛媛, 赵振宇. 利用时序InSAR技术监测南水进京后北京平原地区的地面沉降[J]. 地球物理学进展, 2021, 36(6): 2 351-2 361 (Yan Xia, Liu Yuanyuan, Zhao Zhenyu. Land Subsidence Monitoring after the Start of the South to North Water Transfer in the Beijing Plain Based on Multi-Temporal InSAR[J]. Progress in Geophysics, 2021, 36(6): 2 351-2 361)
(  0) 0) |
| [3] |
Yan Y J, Doin M P, Lopez-Quiroz P, et al. Mexico City Subsidence Measured by InSAR Time Series: Joint Analysis Using PS and SBAS Approaches[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(4): 1 312-1 326 DOI:10.1109/JSTARS.2012.2191146
(  0) 0) |
| [4] |
张双成, 余静, 宋明鑫, 等. 南水北调中线区域地面沉降SBAS-InSAR监测研究[J]. 大地测量与地球动力学, 2022, 42(12): 1 300-1 306 (Zhang Shuangcheng, Yu Jing, Song Mingxin, et al. Land Subsidence Monitoring along the Middle Route of South-North Water Diversion Project by SBAS-InSAR[J]. Journal of Geodesy and Geodynamics, 2022, 42(12): 1 300-1 306)
(  0) 0) |
| [5] |
蒋弥, 李志伟, 丁晓利, 等. InSAR可检测的最大最小变形梯度的函数模型研究[J]. 地球物理学报, 2009, 52(7): 1 715-1 724 (Jiang Mi, Li Zhiwei, Ding Xiaoli, et al. A Study on the Maximum and Minimum Detectable Deformation Gradients Resolved by InSAR[J]. Chinese Journal of Geophysics, 2009, 52(7): 1 715-1 724)
(  0) 0) |
| [6] |
赵峰, 汪云甲, 闫世勇. 时序InSAR技术地表沉降监测结果可靠性及沉降梯度分析[J]. 遥感技术与应用, 2015, 30(5): 969-979 (Zhao Feng, Wang Yunjia, Yan Shiyong. Analysis of the Reliability and Subsidence Gradient for the Subsidence Monitoring Result of Time-Series InSAR[J]. Remote Sensing Technology and Application, 2015, 30(5): 969-979)
(  0) 0) |
| [7] |
金艳, 俞志强, 高晓雄. PSP-InSAR技术在地铁沿线的形变监测应用[J]. 测绘通报, 2020(9): 132-135 (Jin Yan, Yu Zhiqiang, Gao Xiaoxiong. Application of PSP-InSAR Technology in Deformation Monitoring along the Subway[J]. Bulletin of Surveying and Mapping, 2020(9): 132-135)
(  0) 0) |
| [8] |
郭在洁, 陶秋香, 王凤云, 等. SBAS InSAR与GM(1, 1)模型在青岛地铁13号线地表形变监测中的应用[J]. 铁道建筑, 2021, 61(8): 73-78 (Guo Zaijie, Tao Qiuxiang, Wang Fengyun, et al. Application of SBAS InSAR and GM(1, 1) Model in Surface Deformation Monitoring of Qingdao Metro Line 13[J]. Railway Engineering, 2021, 61(8): 73-78)
(  0) 0) |
| [9] |
Taylor S J, Letham B. Forecasting at Scale[J]. The American Statistician, 2018, 72(1): 37-45
(  0) 0) |
| [10] |
谭庆. 基于GAMMA的D-InSAR技术在矿区地面沉降监测中的应用[J]. 测绘与空间地理信息, 2019, 42(5): 233-236 (Tan Qing. Application of Differential InSAR in Monitoring Mining-Induced Subsidence Based on GAMMA Software[J]. Geomatics and Spatial Information Technology, 2019, 42(5): 233-236)
(  0) 0) |
| [11] |
Hooper A J. Persistent Scatter Radar Interferometry for Crustal Deformation Studies and Modeling of Volcanic Deformation[D]. California: Stanford University, 2006
(  0) 0) |
2. Shandong Geo-Surveying and Mapping Institute, 11101 East-Erhuan Road, Ji'nan 250014, China
 2023, Vol. 43
2023, Vol. 43


