2. 31121部队, 南京市, 210001
精密单点定位(precise point positioning,PPP)技术具有无需设立基准站、作业成本低、轻便、精度高等优点,广泛应用于很多行业。但PPP技术需要事后精密产品,无法适用于实时的定位服务。实时动态载波相位差分(real-time kinematic, RTK) 技术可进行高精度实时定位,但需要高精度基准站的支持。传统的标准单点定位(single point positioning, SPP)技术受限于广播星历的精度,定位精度较低,无法满足精密定位的要求。
张熙等[1]评估GPS广播星历精度后发现,GPS广播星历精度逐年提高,2019年GPS空间信号测距误差(signal in space ranging error,SISRE)的RMS优于0.6 m;Steigenberger等[2]评估Galileo广播星历精度后发现,2015~2016年Galileo广播星历的SISRE优于0.3 m。随着BDS完成组网,北斗卫星广播星历的精度不断提高,当前BDS-3卫星的整体轨道精度优于0.23 m,SISRE优于0.5 m[3]。随着各系统广播星历精度的提高,利用广播星历进行实时精密定位成为目前研究的热点。
针对广播星历精度不足的问题,有学者提出基于广播星历PPP的SISRE补偿模型[4-5]。然而,当前SISRE补偿模型主要基于无电离层组合,鲜有基于SISRE补偿的非差非组合模型和针对广播星历精度不足进行补偿策略的研究。基于此,本文利用SISRE补偿策略进行基于广播星历的PPP解算,并对BDS-3和GPS的定位性能进行评估。
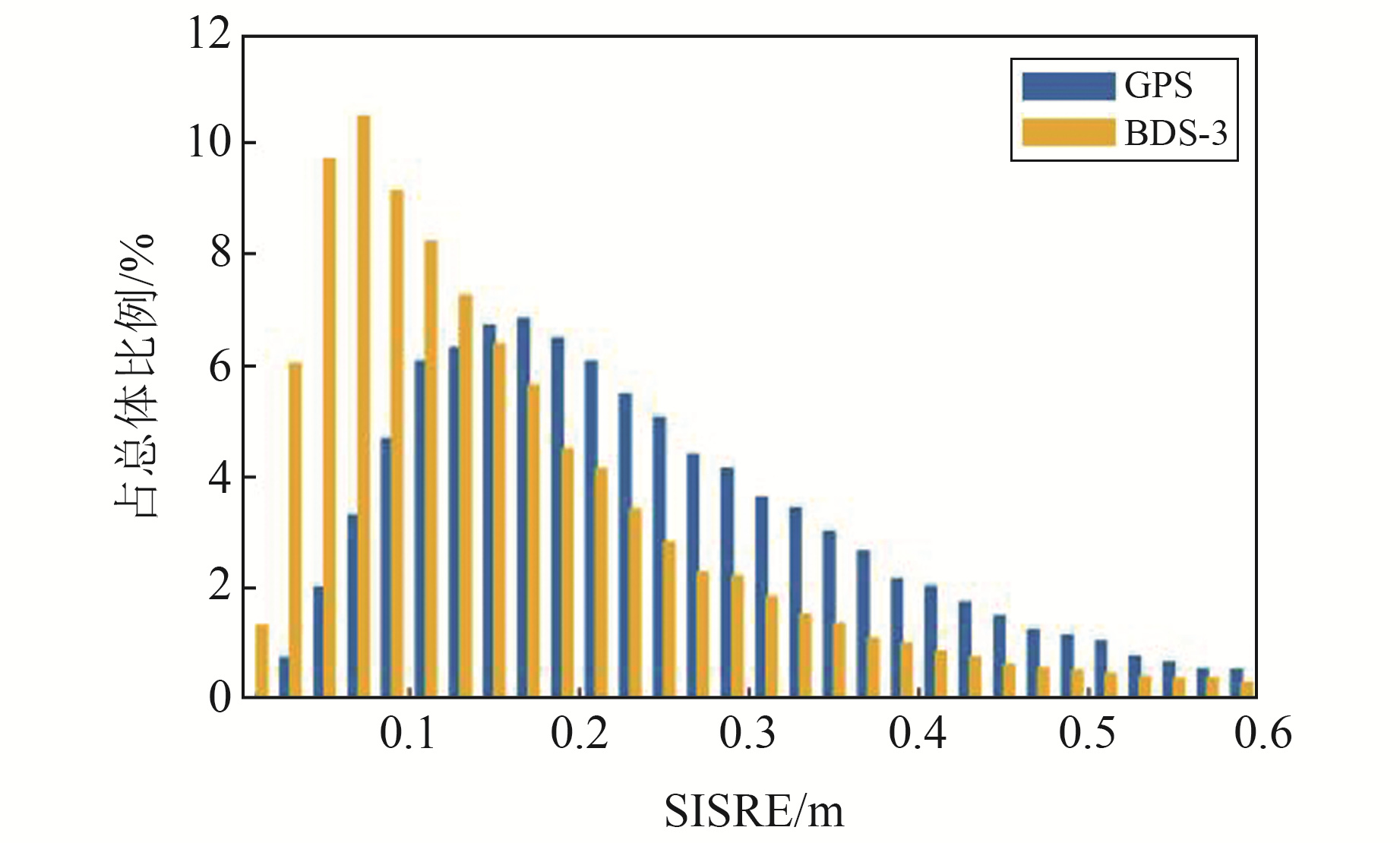
1 广播星历误差特性 1.1 广播星历精度研究基于广播星历的PPP性能时,通常使用SISRE作为衡量标准[6-8]。为了准确描述当前BDS-3和GPS的广播星历精度,对2022-04-10~23 BDS-3和GPS所有健康卫星进行SISRE分析。将MGEX发布的多系统混合广播星历与武汉大学分析中心发布的事后精密星历进行比较,结果见图 1。计算可得,BDS-3和GPS的SISRE均值分别为0.190 m和0.273 m,RMS分别为0.272 m和0.352 m。
|
图 1 GPS和BDS-3 SISRE分布 Fig. 1 Distribution of SISRE of GPS and BDS-3 |
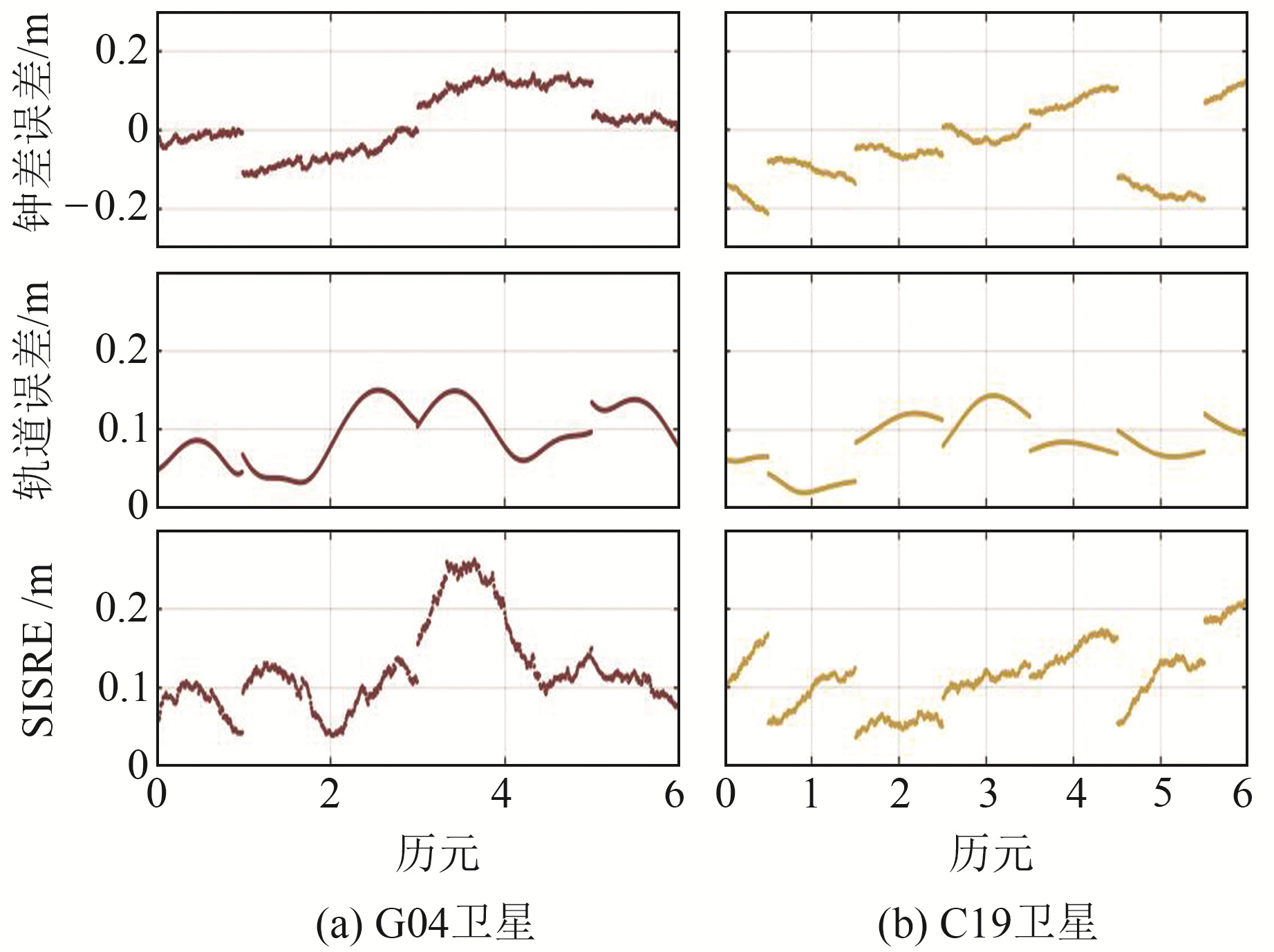
2个相邻时刻广播星历发生切换时,可能会发生突变,从而破环广播星历误差的连续性,因此需要评估BDS-3和GPS的轨道误差、钟差误差和SISRE值的连续性。2022-04-11 00:00~06:00的GPS G04和BDS-3 C19卫星的轨道误差、钟差误差和SISRE值随历元的变化见图 2。
|
图 2 G04和C19卫星各误差值随历元的变化 Fig. 2 The error values of G04 and C19 satellites vary with the epoch |
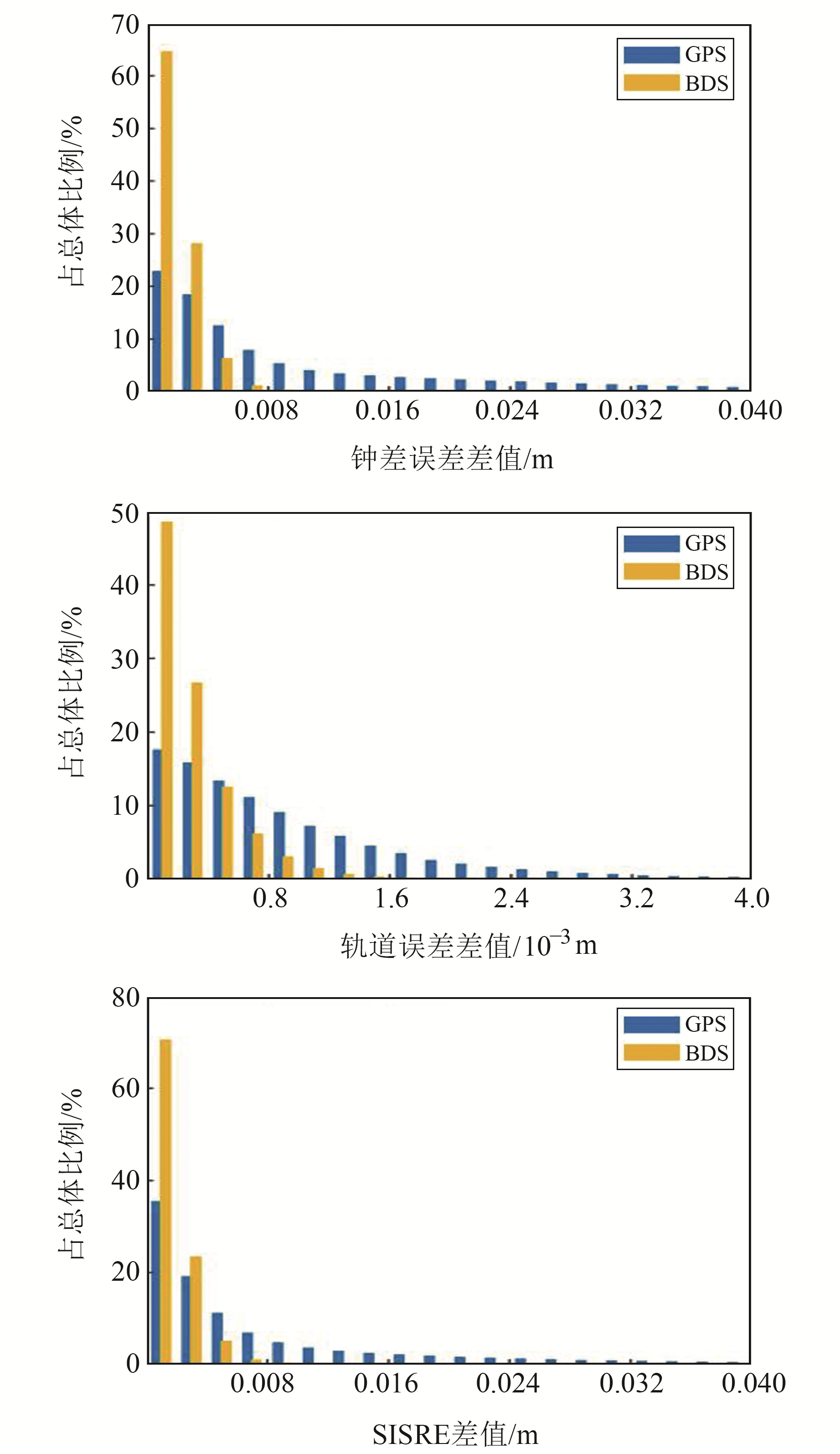
MGEX发布的多系统混合广播星历中,GPS每2 h播发1个广播星历,BDS每1 h播发1个广播星历。由图 2可见,G04和C19各卫星误差量在单个广播星历有效范围内具有连续性,当2个连续批次的广播星历集发生切换时,其误差值会出现跳变。相比于钟差误差,单个广播星历在有效范围内的轨道误差变化较为平滑,但SISRE值受钟差误差影响,在历元间存在较小波动。为了解广播星历轨道误差与钟差误差在历元间的变化大小,以30 s为间隔,对每个广播星历有效范围内相邻2个历元的轨道误差、钟差误差和SISRE值作差,并统计2个系统内所有健康卫星在2022-04-10~23的历元间差值,结果见图 3。由图 3可知,相比于GPS,BDS-3的轨道误差、钟差误差及SISRE值历元间差值较小,其中BDS-3和GPS的SISRE值历元间差值的RMS分别为0.002 3 m和0.015 5 m。
|
图 3 轨道误差、钟差误差和SISRE历元间差值分布 Fig. 3 Distribution of orbital error, clock error and SISRE interepoch difference |
通过上述分析可知,BDS-3和GPS广播星历误差在每个广播星历的有效范围内均表现出较好的连续性,广播星历的误差可以进行随机游走估计,其SISRE值历元间差值的RMS可作为过程噪声。但在2个连续的广播星历发生切换时,其轨道误差、钟差误差及钟差系统性偏差均会出现跳变。因此,在使用参数估计广播星历误差时,可采用随机游走参数估计,但在2个连续的广播星历发生切换时需重新初始化该参数。
2 基于广播星历的PPP模型在PPP的观测方程中,伪距和载波相位观测的函数模型需使用精确的校正数据或模型来消除测量方程中的未知项。伪距和载波相位的原始观测方程为:
| $ \left\{\begin{array}{l} P_i^{\mathrm{s}}=\rho+c \mathrm{~d} t_{\mathrm{r}}-c \mathrm{~d} t^{\mathrm{s}}+m_{\mathrm{w}} T_{\mathrm{w}}+ \\ \quad \gamma_i I_1^{\mathrm{s}}+d_{\mathrm{r}, i}+d_i^{\mathrm{s}}+\varepsilon_i \\ L_i^{\mathrm{s}}=\rho+c \mathrm{~d} t_{\mathrm{r}}-c \mathrm{~d} t^{\mathrm{s}}+m_{\mathrm{w}} T_{\mathrm{w}}- \\ \quad \gamma_i I_1^{\mathrm{s}}+\lambda_i N_i^{\mathrm{s}}+b_{\mathrm{r}, i}+b_i^{\mathrm{s}}+\xi_i \end{array}\right. $ | (1) |
式中,i为观测量频率,Pi、Li分别为第i个频率的伪距和载波相位观测量(单位m),ρ为卫星到接收机的几何项(包含对流层干延迟),dtr、dts分别为接收机钟差和卫星钟差,c为真空中的光速,Tw为测站天顶方向对流层湿延迟,mw为对流层湿延迟映射函数,I1为第1个频率的电离层延迟,Ni为第i个频率的整周模糊度,εi、ξi分别为第i个频率的伪距和载波相位观测值的观测噪声,dr, i、dis分别为第i个频率接收机端和卫星端的伪距硬件延迟,br, i、bis分别为第i个频率接收机端和卫星端的载波相位硬件延迟,λi为第i个频率的波长,γi为电离层延迟影响系数(γi=f12/fi2)。
式(1)经过群延迟(time group delay,TGD)改正后可以表示为:
| $ \left\{\begin{array}{l} p_1^{\mathrm{s}}=u_{\mathrm{r}}^{\mathrm{s}} X+c \mathrm{~d} t_{\mathrm{r}}+S^{\mathrm{s}}+m_{\mathrm{w}} T_{\mathrm{w}}+ \\ \;\;\;I_1^{\mathrm{s}}+d_{\mathrm{r}, 1}+\varepsilon_1 \\ p_3^{\mathrm{s}}=u_{\mathrm{r}}^{\mathrm{s}} X+c \mathrm{~d} t_{\mathrm{r}}+S^{\mathrm{s}}+m_{\mathrm{w}} T_{\mathrm{w}}+ \\ \;\;\;\gamma_3 I_1^{\mathrm{s}}+d_{\mathrm{r}, 3}+\varepsilon_3 \\ l_1^{\mathrm{s}}=u_{\mathrm{r}}^{\mathrm{s}} X+c \mathrm{~d} t_{\mathrm{r}}+S^{\mathrm{s}}+m_{\mathrm{w}} T_{\mathrm{w}}- \\ \;\;\;I_1^{\mathrm{s}}+\lambda_1 N_1^{\mathrm{s}}+b_{\mathrm{r}, 1}+b_1^{\mathrm{s}}-d_3^{\mathrm{s}}+\xi_1 \\ l_3^{\mathrm{s}}=u_{\mathrm{r}}^{\mathrm{s}} X+c \mathrm{~d} t_{\mathrm{r}}+S^{\mathrm{s}}+m_{\mathrm{w}} T_{\mathrm{w}}- \\ \;\;\;\gamma_3 I_1^{\mathrm{s}}+\lambda_3 N_3^{\mathrm{s}}+b_{\mathrm{r}, 3}+b_3^{\mathrm{s}}-d_3^{\mathrm{s}}+\xi_3 \end{array}\right. $ | (2) |
式中,pis和lis分别为伪距和载波相位观测值减去计算值(计算值包括卫星钟差dt3s及相应的TGD改正)后的数据,urs为接收机到卫星连线的方向余弦,X为三维坐标改正数,Ss为广播星历误差在测距方向上的影响,即卫星广播星历的SISRE。
2.1 基于广播星历的非差非组合PPP模型SISRE补偿通过引入新的参数来描述广播星历误差,或是通过已有参数吸收广播星历误差。本文对比2种SISRE补偿模型:1)在无电离层组合的基础上引入参数Ss来描述广播星历误差,并对其进行随机游走估计[4];2)以非差非组合模型为基础,利用相位模糊度吸收广播星历误差。
为方便公式推导,定义以下变量:
| $ \left\{ {\begin{array}{*{20}{l}} {{\alpha _{ij}} = \frac{{f_i^2}}{{f_i^2 - f_j^2}}}\\ {{\beta _{ij}} = - \frac{{f_j^2}}{{f_i^2 - f_j^2}}}\\ {d_{{\rm{I}}{{\rm{F}}_{ij}}}^{\rm{s}} = {\alpha _{ij}}d_i^{\rm{s}} + {\beta _{ij}}d_j^{\rm{s}}}\\ {{d_{{\rm{r}},{\rm{I}}{{\rm{F}}_{ij}}}} = {\alpha _{ij}}{d_{{\rm{r}},i}} + {\beta _{ij}}{d_{{\rm{r}},j}}}\\ {b_{{\rm{I}}{{\rm{F}}_{ij}}}^{\rm{s}} = {\alpha _{ij}}b_i^{\rm{s}} + {\beta _{ij}}b_j^{\rm{s}}}\\ {{b_{{\rm{r}},I{{\rm{F}}_{ij}}}} = {\alpha _{ij}}{b_{{\rm{r}},i}} + {\beta _{ij}}{b_{{\rm{r}},j}}}\\ {{\rm{DC}}{{\rm{B}}_{{\rm{r}},ij}} = {d_{{\rm{r}},i}} - {d_{{\rm{r}},j}}} \end{array}} \right. $ | (3) |
相比于无电离层组合,虽然非差非组合模型的观测方程观测值噪声较小,但无法消除电离层延迟的影响,需要引入电离层延迟参数。若此时再引入广播星历误差参数,将会引起观测方程的系数阵秩亏。因此,采用降低观测值权重的方法,削弱广播星历精度不足的影响。
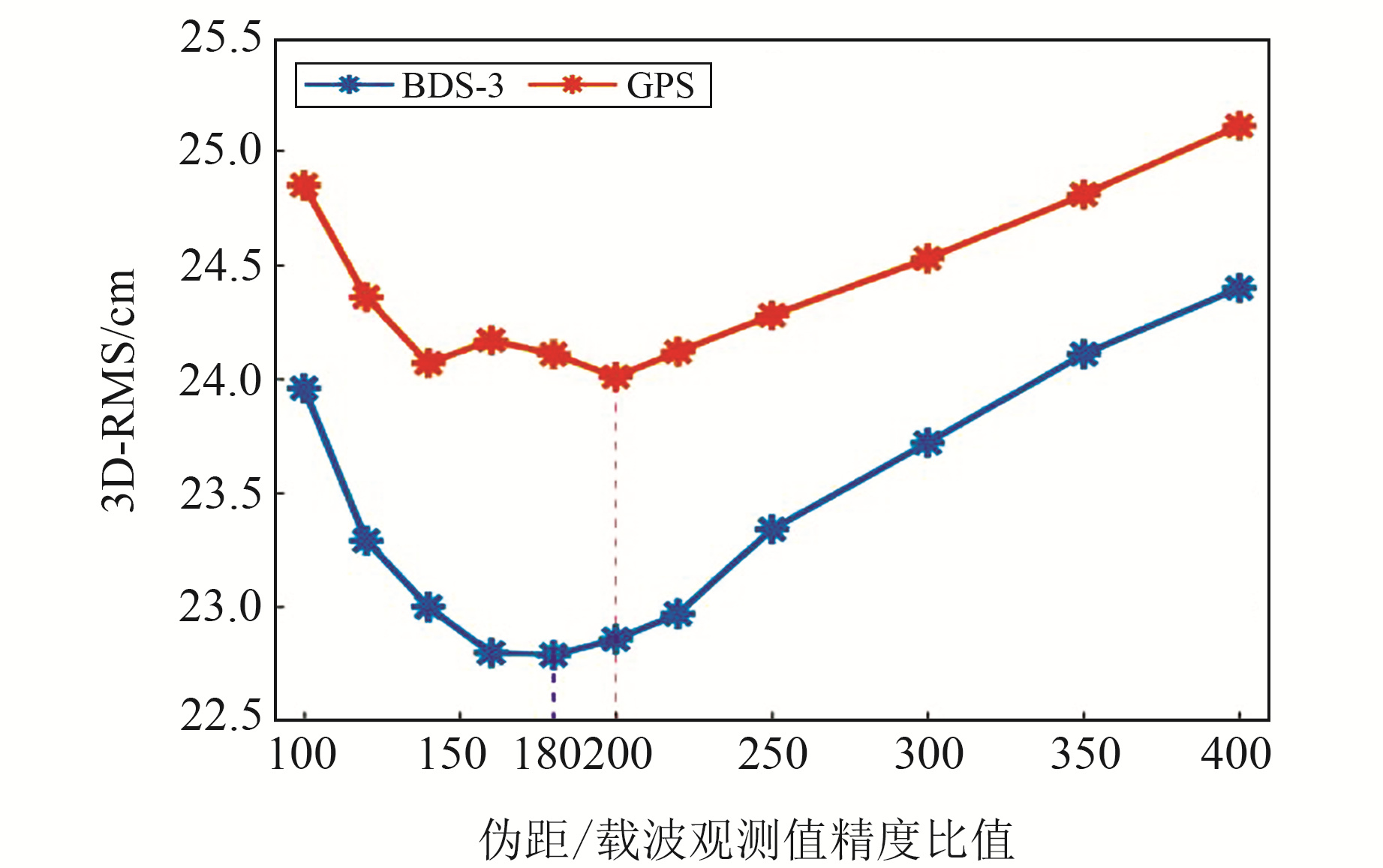
图 4为GPS和BDS-3三维定位精度随伪距/载波观测量精度比值的变化。由图 4可知,GPS和BDS-3伪距观测量与载波相位观测量误差的比值分别选用200和180时,三维定位精度最好。载波相位观测方程的广播星历误差部分由浮点模糊度吸收,将模糊度作为随机游走参数进行估计。通过式(2)可进一步推导非差非组合观测方程:
|
图 4 三维定位精度随伪距/载波观测值精度比值的变化 Fig. 4 Variation of 3D positioning accuracy with accuracy ratio of pseudo-distance/carrier observation value |
| $ \left\{\begin{array}{l} p_1^{\mathrm{s}}=u_{\mathrm{r}}^{\mathrm{s}} X+c \overline{\mathrm{d}} t_{\mathrm{r}}+m_{\mathrm{w}} T_{\mathrm{w}}+\bar{I}_1^{\mathrm{s}}+\varepsilon_1 \\ p_3^{\mathrm{s}}=u_{\mathrm{r}}^{\mathrm{s}} X+c \overline{\mathrm{d}} t_{\mathrm{r}}+m_{\mathrm{w}} T_{\mathrm{w}}+\gamma_3 \bar{I}_1^{\mathrm{s}}+\varepsilon_3 \\ l_1^{\mathrm{s}}=u_{\mathrm{r}}^{\mathrm{s}} X+c \overline{\mathrm{d}} t_{\mathrm{r}}+m_{\mathrm{w}} T_{\mathrm{w}}-\bar{I}_1^{\mathrm{s}}+\bar{N}_1^{\mathrm{s}}+\xi_1 \\ l_3^{\mathrm{s}}=u_{\mathrm{r}}^{\mathrm{s}} X+c \overline{\mathrm{d}} t_{\mathrm{r}}+m_{\mathrm{w}} T_{\mathrm{w}}-\gamma_3 \bar{I}_1^{\mathrm{s}}+\bar{N}_3^{\mathrm{s}}+\xi_3 \end{array}\right. $ | (4) |
式中,
| $ \overline {\bf{X}} = {\rm{ }}\left[ {{x_{\rm{r}}},{y_{\rm{r}}},{z_{\rm{r}}},c\overline {\rm{d}} {t_{\rm{r}}},{T_{\rm{w}}},\bar I_{{1^1}}^{\rm{s}}, \cdots ,\bar I_{{1^n}}^{\rm{s}},} \right.\left. {\bar N_{{1^1}}^{\rm{s}}, \cdots ,\bar N_{{1^n}}^{\rm{s}},\bar N_{{3^1}}^{\rm{s}}, \cdots ,\bar N_{{3^n}}^{\rm{s}}} \right] $ | (5) |
将非差非组合状态向量中的静态坐标参数作为常数估计,标准单点定位结果作为初值;将动态坐标参数作为白噪声估计,标准单点定位结果作为各历元初值。考虑到接收机为高频信号,采用白噪声估计最为合适,标准单点定位解算钟差作为每历元初值。天顶对流层湿延迟采用随机游走参数估计,由于湿延迟通常小于0.3 m,可选取一个较小的常数作为初值,参照GAMP软件将初值设为0.15 m。电离层延迟参数采用随机游走估计,通过双频伪距观测值得到初值。相位模糊度由于吸收了广播星历误差,选择随机游走估计,初值通过伪距观测值与相位观测值作差得到。
2.2 参数配置为分析本文所提模型的定位性能,对比以下4种模型的计算结果:
1) 模型1:采用事后精密产品进行传统PPP(无电离层组合PPP)模型解算;
2) 模型2:使用广播星历代替精密星历进行传统PPP模型解算;
3) 模型3:使用广播星历,采用SISRE补偿的无电离层组合PPP模型进行解算[8];
4) 模型4:使用广播星历,采用SISRE补偿的非差非组合PPP模型进行解算。
模型1、2的状态向量参数元素估计方法与传统PPP模型相同,模型3、4的状态向量参数元素采用本文的参数估计方法。在滤波过程中,随机游走的参数过程噪声设置为q=σp2Δt/τp,σp为过程噪声标准差,τp为时间常数,Δt为时间间隔。采用白噪声参数估计接收机钟差,其过程噪声设置为q=σp2,不考虑时间间隔,表示钟差的标准差不随历元变化,这样接收机钟差就可被视为白噪声。状态向量各参数的初始标准差σ0、过程噪声标准差σp和时间间隔Δt的设置见表 1。
|
|
表 1 状态向量元素的卡尔曼滤波噪声设置 Tab. 1 Kalman filter noise settings of state vector elements |
实验采用15个MGEX测站2022-04-10~16的观测数据,测站分布见图 5。PPP解算时,使用武汉大学分析中心发布的15 min事后精密星历;BDS卫星采用BDS官方2019-12-30发布的天线改正文件;GPS卫星采用IGS发布的天线改正文件;广播星历采用MEGX发布的多系统混合广播星历。BDS-3使用B1I和B3I双频观测值,GPS采用L1和L2双频观测值。观测数据采样间隔为30 s,观测值方差采用高度角定权法,截止高度角设置为7°。GPS和BDS-3载波相位观测值标准差设为0.003 m,伪距观测值的标准差设置为0.3 m。对天顶方向湿延迟进行对流层延迟部分估计。采用卡尔曼滤波模型估计测站坐标,并将IGS当周发布的SINEX文件中测站坐标作为参考值,计算PPP解算结果的定位误差。

|
图 5 MGEX测站分布 Fig. 5 Distribution of MGEX stations |
计算每日MEGX测站数据24 h解,分析4种模型静态和仿动态模式下的定位性能。评估定位精度时,统计收敛后的定位结果(认为3 h后的结果为收敛后结果)。
为研究BDS-3和GPS的定位性能,分别计算二者的单星座解。此外,对双星座GPS+BDS-3的定位精度进行估计,可为研究本文定位模型在多GNSS定位中的应用及大量跟踪卫星对定位精度的影响提供可能。
3.2.1 静态定位性能4种定位模型静态定位误差的RMS见表 2。由表可见,模型1三维定位误差的RMS优于2 cm,证明了所采用PPP模型和算法的有效性。使用模型2时,GPS和BDS-3在高程方向上的定位误差的RMS约为0.3 m,水平方向上的定位误差的RMS约为0.2 m,三维定位误差的RMS约为0.4 m。由于BDS-3广播星历的精度高于GPS,因此其定位精度略优于GPS。模型3、4的定位精度相比于模型2在高程和水平方向上均有不同程度的提高,且在高程方向上的提高较为显著。模型3的GPS和BDS-3三维定位精度分别约为23 cm和20 cm,相比于模型2提高约42.3%和44.6%;模型4的GPS和BDS-3三维定位精度分别约为24 cm和23 cm,相比于模型2提高约39.1%和37.0%。2种改进模型的定位精度相当,模型3略优于模型4。2个系统组合后,可观测卫星数量增加,水平和高程方向上的定位精度相比于单系统均有所提升,其中水平方向上的提升较为显著。模型3、4双系统静态三维定位精度可分别达到约16 cm和18 cm。
|
|
表 2 不同定位模型的静态定位精度 Tab. 2 Static positioning accuracy of different positioning models |
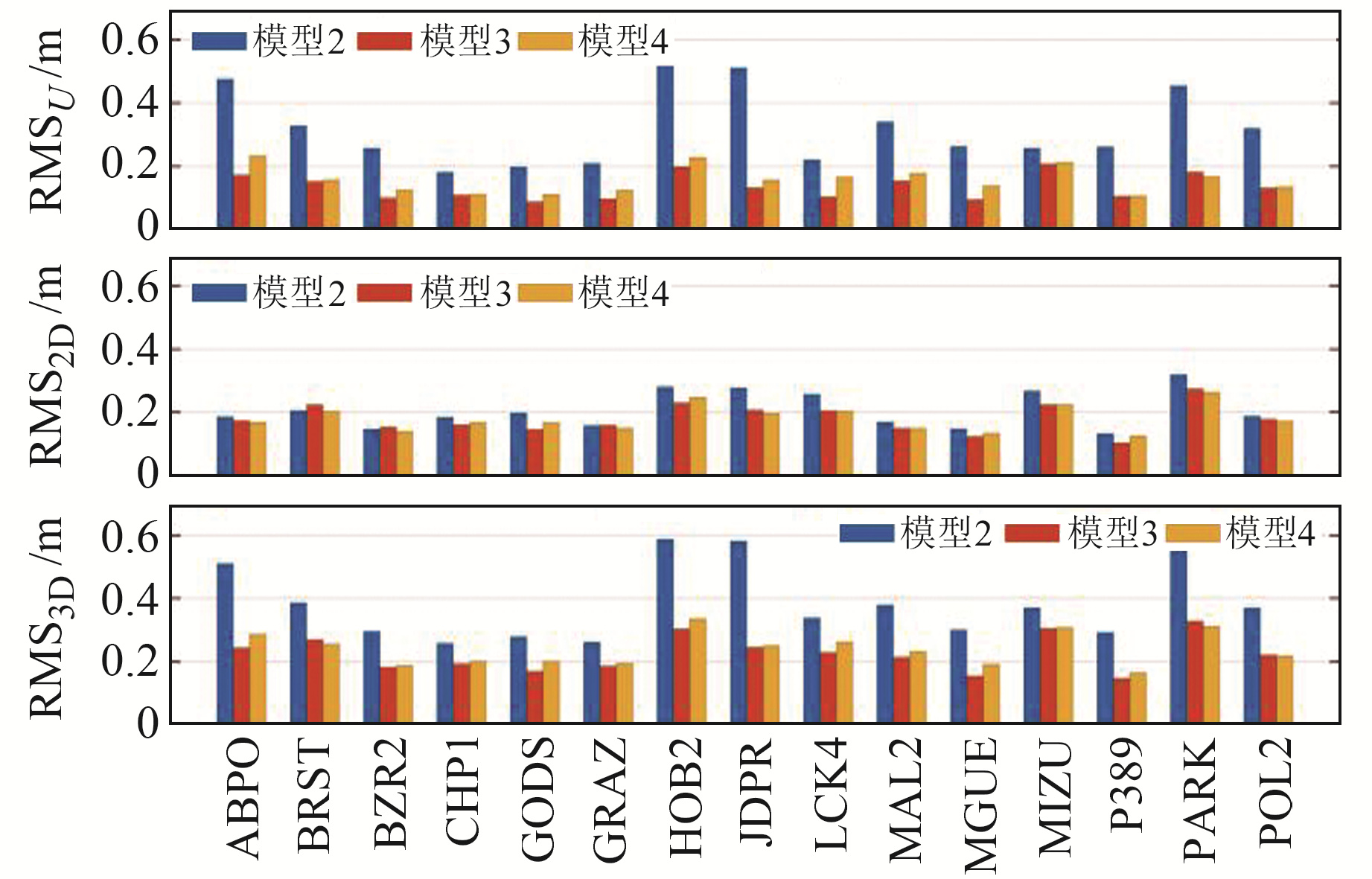
图 6、7分别为GPS和BDS-3各测站使用3种基于广播星历定位模型时的定位精度。由图可见,相比于模型2,各测站SISRE补偿后模型的三维定位精度有所提升,U方向上的精度提升显著,水平方向的精度提升较少。GPS和BDS-3在采用SISRE补偿的定位模型后,大部分测站在U方向和水平方向上的定位误差优于0.2 m。为了更深入地分析SISRE补偿模型对定位的影响,绘制静态条件下使用4种不同模型获得的POL2测站24 h坐标误差时间序列,见图 8。可以看出,采用SISRE补偿后,模型3、4的定位精度相比模型2有所提升,特别是在U方向上更明显。
|
图 6 GPS基于广播星历的3种定位模型下的静态定位精度 Fig. 6 Static positioning accuracy of three positioning models of GPS based on broadcast ephemeris |

|
图 7 BDS-3基于广播星历的3种定位模型的静态定位精度 Fig. 7 Static positioning accuracy of three positioning models of BDS-3 based on broadcast ephemeris |

|
图 8 POL2测站静态条件下4种模型定位结果误差时间序列 Fig. 8 Time series of positioning errors of four models under static condition at POL2 station |
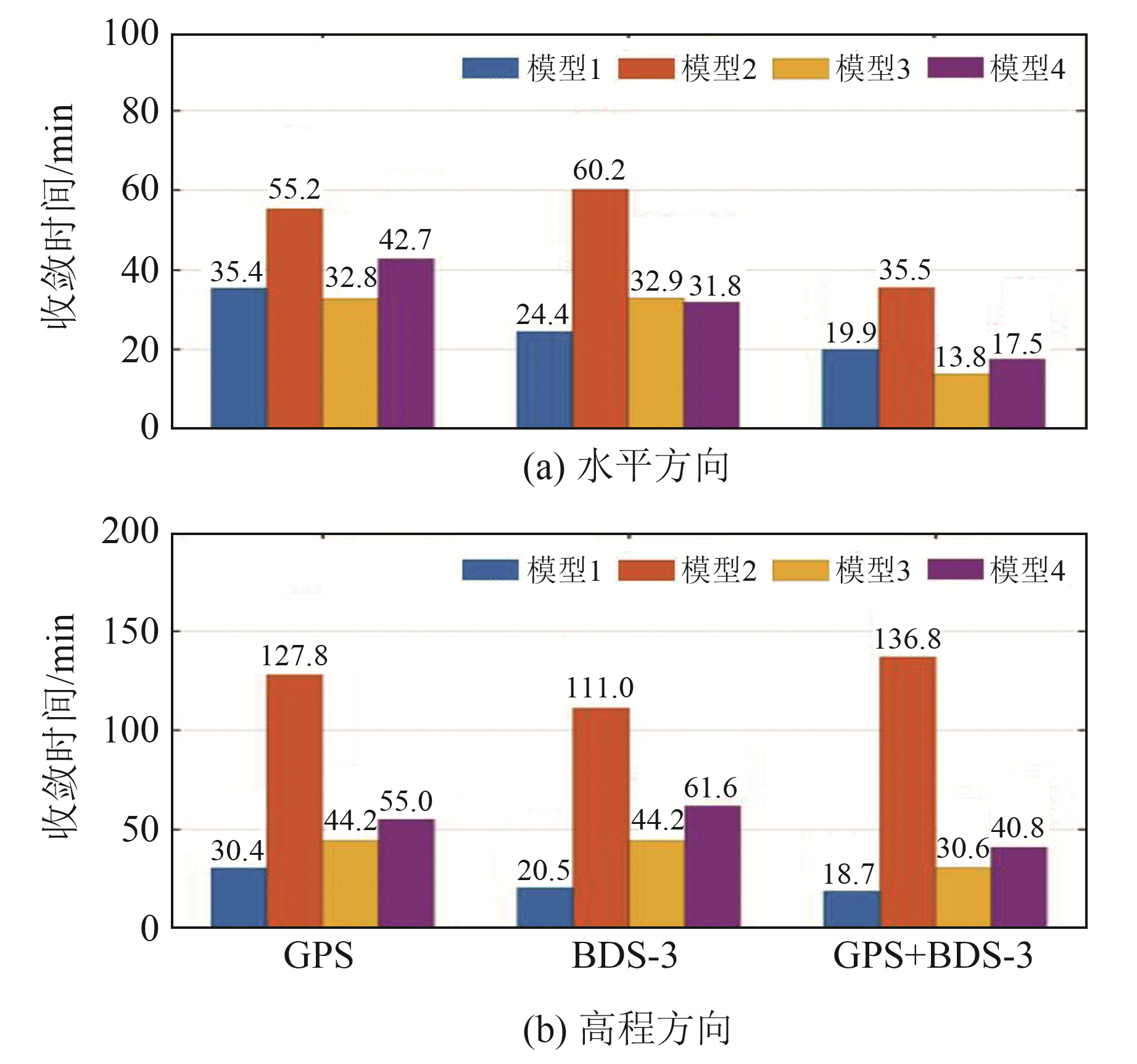
图 9为GPS、BDS-3以及GPS/BDS-3双系统采用不同定位模型时的高程和水平方向上的收敛时间。将高程方向上连续40个历元小于阈值、水平方向上E和N方向上连续40个历元同时小于阈值作为收敛条件。考虑到采用不同星历产品定位模型的定位精度相差较大,将模型1的收敛阈值设置为0.1 m,另外3种模型的收敛阈值设置为0.5 m。由图 9可知,采用模型1进行定位时,GPS的收敛时间约为30~35 min,BDS-3的收敛时间约为20~25 min,组合系统的收敛时间有所减少;模型2的收敛时间较长;模型3、4相比于模型2在高程和水平方向上的收敛时间均明显减少。
|
图 9 各系统采用4种模型在水平和高程方向上的收敛时间 Fig. 9 Convergence time of four models in horizontal and elevation directions for each system |
4种定位模型仿动态定位误差的RMS见表 3。由表 3可知,模型1三维定位误差的RMS优于7 cm,证明了所采用的动态PPP模型和算法的有效性。使用模型2时,GPS和BDS-3在高程方向上的定位误差的RMS约为1 m,水平方向上的定位误差的RMS约为0.6 m,三维定位误差的RMS约为1.2 m。模型3、4的定位精度相比于模型2在高程和水平方向上均有所提高,且在高程方向上的提高较为显著。模型3的GPS和BDS-3三维定位精度分别约为75 cm和80 cm,相比于模型2提高约35.3%和34.7%;模型4的GPS和BDS-3三维定位精度分别约为73 cm和74 cm,相比于模型2提高37.5%和39.7%。2个系统组合后,4种模型下的水平和高程方向上的定位精度相比于单系统均有明显提升,模型3、4双系统仿动态三维定位精度分别可达约40 cm和45 cm。
|
|
表 3 不同定位模型的仿动态定位精度 Tab. 3 Simulation dynamic positioning accuracy of different positioning models |
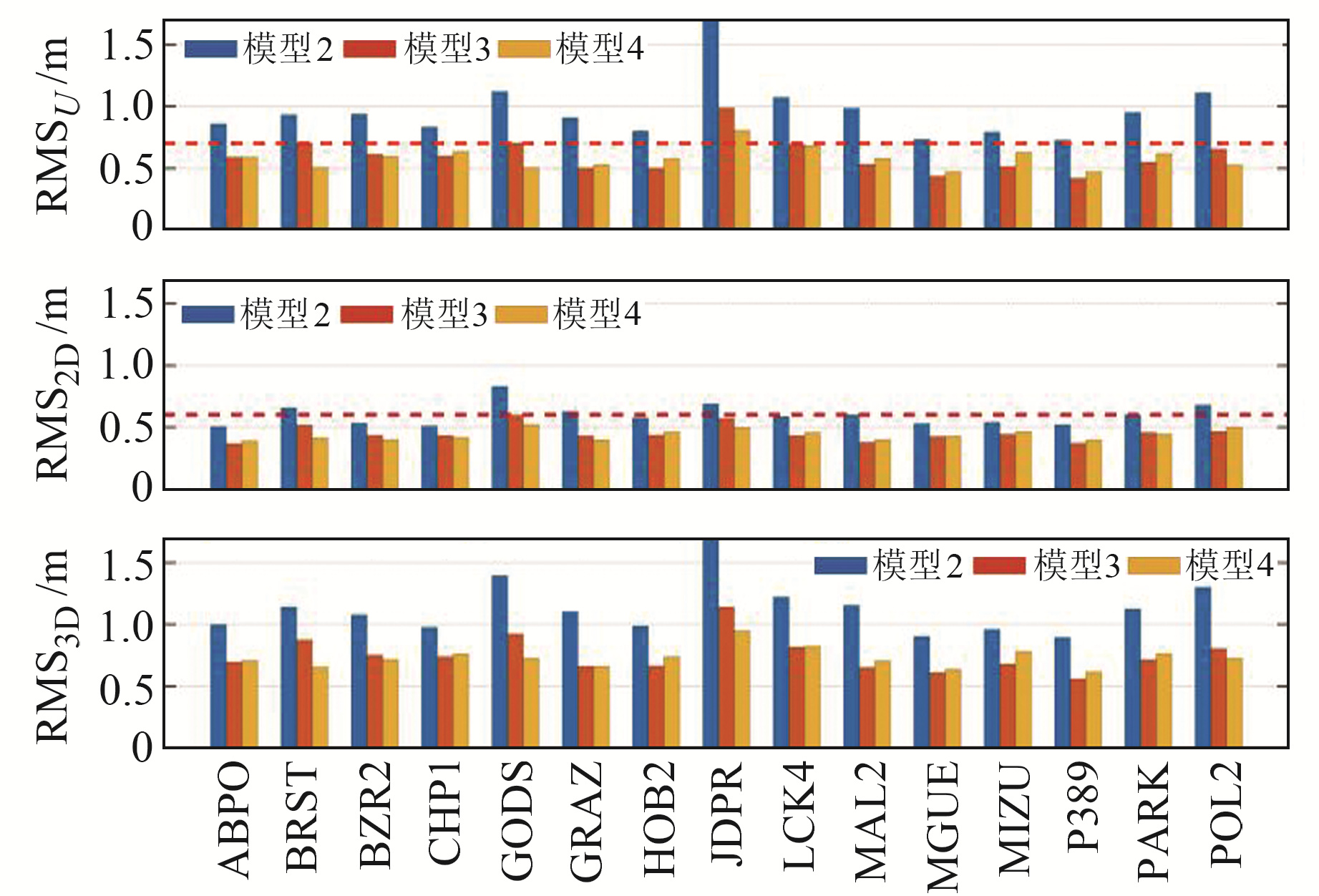
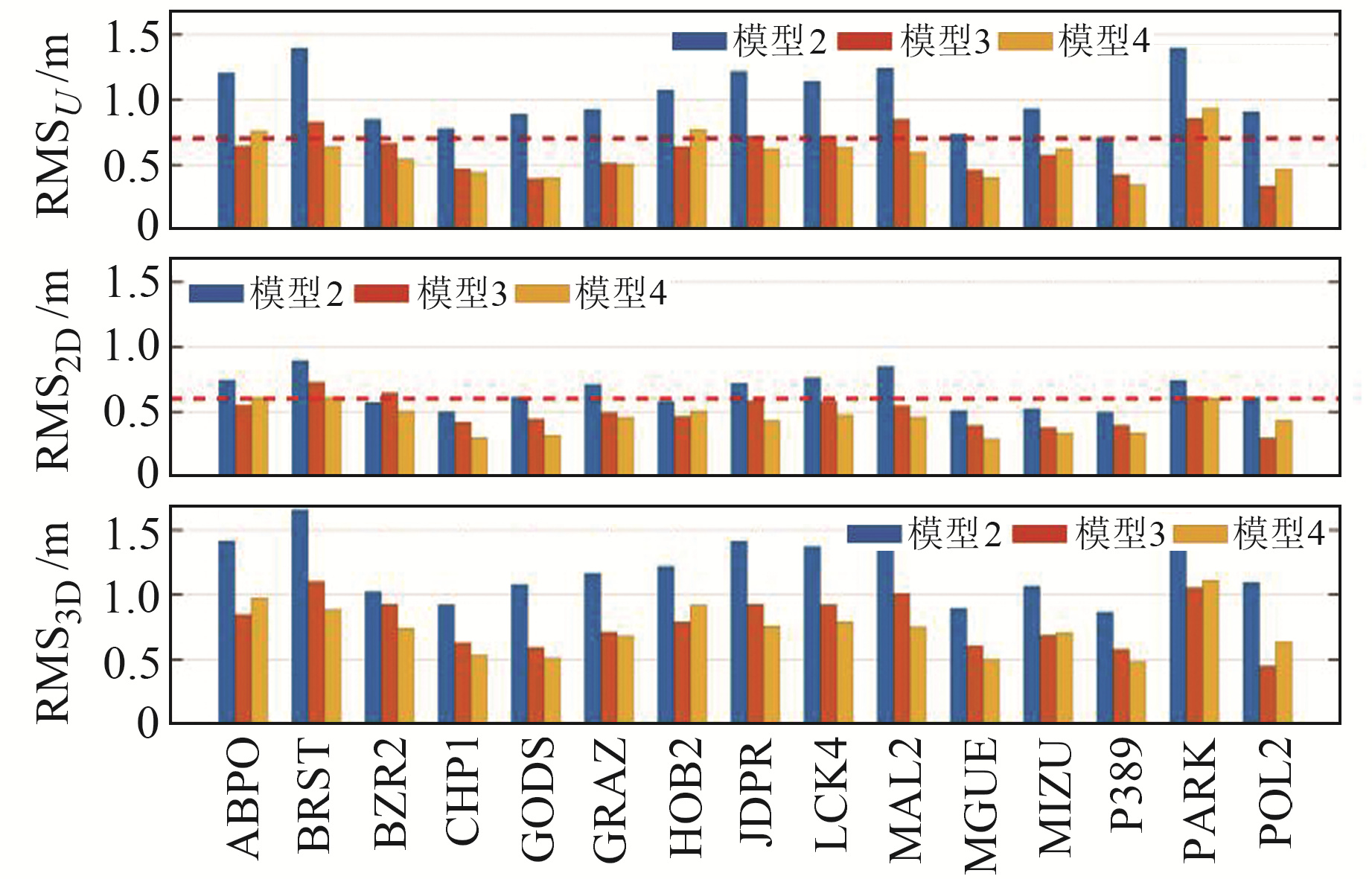
图 10、11为GPS和BDS-3各测站使用3种基于广播星历定位模型时的定位误差的RMS。由图可见,各测站SISRE补偿后模型的高程、水平和三维方向上的定位精度相比于模型2均有不同程度的提高,说明SISRE补偿模型能有效提高动态定位精度。GPS和BDS-3在采用2种SISRE补偿的定位模型后,大部分测站在高程和水平方向上的定位误差的RMS分别优于0.7 m和0.6 m。
|
图 10 GPS基于广播星历的3种定位模型的仿动态定位精度 Fig. 10 Simulation dynamic positioning accuracy of three positioning models of GPS based on broadcast ephemeris |
|
图 11 BDS-3基于广播星历的3种定位模型的仿动态定位精度 Fig. 11 Simulation dynamic positioning accuracy of three positioning models of BDS-3 based on broadcast ephemeris |
1) 在静态定位模式下,模型3的GPS、BDS-3和GPS/BDS-3的三维定位误差的RMS分别约为0.23 m、0.20 m和0.16 m,相比于模型2分别提升42.3%、44.6%和52.3%;模型4的GPS、BDS-3和GPS/BDS-3的三维定位误差的RMS分别约为0.24 m、0.23 m和0.18 m,相比于模型2分别提升39.1%、37.0%和47.6%。2种SISRE补偿模型定位精度相当,模型3的精度略高于模型4。在收敛时间方面,模型3、4的收敛速度相比于模型2均有明显提升,模型3的收敛速度略快,且采用双系统定位时的收敛速度快于单系统。
2) 在仿动态定位模式下,模型3的GPS、BDS-3和GPS/BDS-3的三维定位误差的RMS分别约为0.75 m、0.80 m和0.40 m,相比于模型2分别提升35.3%、34.7%和47.1%;模型4的GPS、BDS-3和GPS/BDS-3的三维定位误差的RMS分别为0.73 m、0.74 m和0.45 m,相比于模型2分别提升37.5%、39.7%和41.1%。2种SISRE补偿模型仿动态定位精度相当,且均能有效提升定位精度。
| [1] |
张熙, 刘长建, 章繁, 等. GPS广播星历长期数据质量分析[J]. 测绘科学技术学报, 2020, 37(2): 144-148 (Zhang Xi, Liu Changjian, Zhang Fan, et al. Long-Term Quality Analysis on GPS Broadcast Ephemeris Data[J]. Journal of Geomatics Science and Technology, 2020, 37(2): 144-148)
(  0) 0) |
| [2] |
Steigenberger P, Montenbruck O. Galileo Status: Orbits, Clocks, and Positioning[J]. GPS Solutions, 2017, 21(2): 319-331 DOI:10.1007/s10291-016-0566-5
(  0) 0) |
| [3] |
姚文豪, 李方超, 高文亮, 等. BDS-3在轨卫星广播星历精度评估[J]. 测绘科学, 2022, 47(7): 1-8 (Yao Wenhao, Li Fangchao, Gao Wenliang, et al. Accuracy Evaluation of BDS-3 Satellite Broadcast Ephemeris[J]. Science of Surveying and Mapping, 2022, 47(7): 1-8)
(  0) 0) |
| [4] |
Carlin L, Hauschild A, Montenbruck O. Precise Point Positioning with GPS and Galileo Broadcast Ephemerides[J]. GPS Solutions, 2021, 25(2): 77 DOI:10.1007/s10291-021-01111-4
(  0) 0) |
| [5] |
Chen G, Wei N, Li M, et al. BDS-3 and GPS/Galileo Integrated PPP Using Broadcast Ephemerides[J]. GPS Solutions, 2022, 26(4): 129 DOI:10.1007/s10291-022-01311-6
(  0) 0) |
| [6] |
Montenbruck O, Steigenberger P, Hauschild A. Broadcast Versus Precise Ephemerides: A Multi-GNSS Perspective[J]. GPS Solutions, 2015, 19(2): 321-333 DOI:10.1007/s10291-014-0390-8
(  0) 0) |
| [7] |
景鑫, 车通宇, 周舒涵, 等. 北斗三号系统开通前后广播星历精度对比分析[J]. 全球定位系统, 2022, 47(4): 23-30 (Jing Xin, Che Tongyu, Zhou Shuhan, et al. Comparative Analysis of Broadcast Ephemeris Accuracy before and after the Opening of BDS-3 System[J]. GNSS World of China, 2022, 47(4): 23-30)
(  0) 0) |
| [8] |
Wu W W, Guo F, Zheng J Z. Analysis of Galileo Signal-in-Space Range Error and Positioning Performance during 2015-2018[J]. Satellite Navigation, 2020, 1(1): 1-13 DOI:10.1186/s43020-019-0006-0
(  0) 0) |
2. 31121 Troops of PLA, Nanjing 210001, China
 2023, Vol. 43
2023, Vol. 43

