集中式卡尔曼滤波器是实现多传感器组合导航系统的最优估计方法，但是由于其状态维数高，存在计算负担重、容错性差、通信负担重等缺点。随着计算机技术的发展，计算负担重的困难得到缓解，但对容错和估计精度的要求却越来越高^[1]。基于分布式滤波方法，联邦滤波器可增强系统的容错性与可靠性^[2]，且设计灵活，便于工程实现，但其精度低于集中式卡尔曼滤波器^[3]。为解决系统模型误差导致的滤波精度下降的问题，扩展卡尔曼滤波、无迹卡尔曼滤波和容积卡尔曼滤波等非线性滤波相继被提出^[4]，然而相对常规的线性卡尔曼滤波，这些方法存在工程实现难的缺陷。为克服量测噪声统计特性不准确导致的滤波精度下降的问题，自适应卡尔曼滤波技术不断发展，主要包括基于新息的自适应估计方法(IAE)和贝叶斯方法^[5]。变分贝叶斯方法是对实际过程中实现难度较大的贝叶斯方法的改进，其核心思想是对贝叶斯密度分布函数进行近似，可以实现量测噪声统计特性的次优估计。

本文在集中式卡尔曼滤波的基础上推导了分布式卡尔曼滤波的一种表达式方法，该方法不仅保留了集中式卡尔曼滤波技术的最优性，而且具有故障识别与自动隔离、系统自动重组的特点。以此为基础，结合变分贝叶斯估计方法提出一种组合导航系统的自适应分布式滤波算法。

1 自适应分布式滤波模型 1.1 集中式卡尔曼滤波

综合考虑主导航系统及各子导航系统，设多传感器组合导航系统的状态方程为：

$\boldsymbol{X}_{k+1}= \mathit{\boldsymbol{\boldsymbol{\varPhi}}}_{k+1, k} \boldsymbol{X}_k+ \mathit{\boldsymbol{\boldsymbol{\varGamma}}}_k \boldsymbol{W}_k$

(1)

各子导航系统的量测方程可表示为：

$\boldsymbol{Z}_{k+1}^i=\boldsymbol{H}_{k+1}^i \boldsymbol{X}_{k+1}+\boldsymbol{V}_{k+1}^i$

(2)

其中，$\boldsymbol{Z}_{k+1}^i \in \boldsymbol{R}^{m_i}$为量测向量，$\boldsymbol{H}_{k+1}^i$为量测矩阵，$\boldsymbol{V}_{k+1}^i \in \boldsymbol{R}^{m_i}$为均值为0、相互独立的高斯序列，且

$E\left\{\left[\begin{array}{c} \boldsymbol{W}_k \\ \boldsymbol{V}_{k+1}^i \end{array}\right]\left[\begin{array}{ll} \boldsymbol{W}_l^{\mathrm{T}} & \left(\boldsymbol{V}_{l+1}^i\right)^{\mathrm{T}} \end{array}\right]\right\}=\left[\begin{array}{cc} \boldsymbol{Q}_k \boldsymbol{\delta}_{k, l} & 0 \\ 0 & \boldsymbol{R}_k^i \delta_{k+1, l+1} \end{array}\right]$

故集中式卡尔曼滤波器量测方程为：

$\boldsymbol{Z}_{k+1}=\boldsymbol{H}_{k+1} \boldsymbol{X}_{k+1}+\boldsymbol{V}_{k+1}$

(3)

式中，$\boldsymbol{Z}_{k+1}=\left[\left(\boldsymbol{Z}_{k+1}^1\right)^{\mathrm{T}},\left(\boldsymbol{Z}_{k+1}^2\right)^{\mathrm{T}}, \cdots,\left(\boldsymbol{Z}_{k+1}^{\mathrm{N}}\right)^{\mathrm{T}}\right]^{\mathrm{T}},$$\boldsymbol{H}_{k+1}=\left[\left(\boldsymbol{H}_{k+1}^1\right)^{\mathrm{T}},\left(\boldsymbol{H}_{k+1}^2\right)^{\mathrm{T}}, \cdots,\left(\boldsymbol{H}_{k+1}^{\mathrm{N}}\right)^{\mathrm{T}}\right]^{\mathrm{T}},$ $\boldsymbol{V}_{k+1}=\left[\left(\boldsymbol{V}_{k+1}^1\right)^{\mathrm{T}},\left(\boldsymbol{V}_{k+1}^2\right)^{\mathrm{T}}, \cdots,\left(\boldsymbol{V}_{k+1}^{\mathrm{N}}\right)^{\mathrm{T}}\right]^{\mathrm{T}}$

且

$\begin{gathered} E\left\{\left[\begin{array}{c} \boldsymbol{W}_k \\ \boldsymbol{V}_{k+1} \\ \tilde{\boldsymbol{X}}_{0 \mid 0} \end{array}\right]\left[\begin{array}{lll} \boldsymbol{W}_l^{\mathrm{T}} & \boldsymbol{V}_{l+1}^{\mathrm{T}} & \tilde{\boldsymbol{X}}_{0 \mid 0}^{\mathrm{T}} \end{array}\right]\right\}= \\ {\left[\begin{array}{ccc} \boldsymbol{Q}_k \delta_{k l} & 0 & 0 \\ 0 & \boldsymbol{R}_k \delta_{k+1, l+1} & \\ 0 & 0 & \boldsymbol{P}_{0 \mid 0} \end{array}\right]} \end{gathered}$

其中，

$\boldsymbol{R}_{k+1}^{-1}=\operatorname{diag}\left\{\left(\boldsymbol{R}_{k+1}^1\right)^{-1}, \left(\boldsymbol{R}_{k+1}^2\right)^{-1}, \cdots, \left(\boldsymbol{R}_{k+1}^N\right)^{-1}\right\}$

(4)

集中式卡尔曼滤波器的状态估计方程为：

$\begin{gathered} \hat{\boldsymbol{X}}_{k+1 \mid k+1}= \\ \hat{\boldsymbol{X}}_{k+1 \mid k}+\boldsymbol{K}_{k+1}\left[\boldsymbol{Z}_{k+1}-\boldsymbol{H}_{k+1} \hat{\boldsymbol{X}}_{k+1 \mid k}\right] \end{gathered}$

(5)

$\hat{\boldsymbol{X}}_{k+1 \mid k}= \mathit{\boldsymbol{\boldsymbol{\varPhi}}}_{k+1, k} \hat{\boldsymbol{X}}_{k \mid k}$

(6)

$\begin{gathered} \boldsymbol{K}_{k+1}=\boldsymbol{P}_{k+1 \mid k+1} \boldsymbol{H}_{k+1}^{\mathrm{T}} \boldsymbol{R}_{k+1}^{-1}= \\ \boldsymbol{P}_{k+1 \mid k+1}\left[\left(\boldsymbol{H}_{k+1}^1\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^1\right)^{-1}, \cdots, \right. \\ \left.\left(\boldsymbol{H}_{k+1}^N\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^N\right)^{-1}\right]=\left[\boldsymbol{K}_{k+1}^1, \cdots, \boldsymbol{K}_{k+1}^N\right] \end{gathered}$

(7)

$\begin{gathered} \boldsymbol{P}_{k+1 \mid k+1}^{-1}=\boldsymbol{P}_{k+1 \mid k}^{-1}+\boldsymbol{H}_{k+1}^{\mathrm{T}} \boldsymbol{R}_{k+1}^{-1} \boldsymbol{H}_{k+1}=\boldsymbol{P}_{k+1 \mid k}^{-1}+ \\ \sum\limits_{i=1}^N\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^i\right)^{-1} \boldsymbol{H}_{k+1}^i=\boldsymbol{P}_{k+1 \mid k}^{-1}+ \\ \sum\limits_{i=1}^N\left[\left(\boldsymbol{P}_{k+1 \mid k+1}^i\right)-1-\left(\boldsymbol{P}_{k+1 \mid k}^i\right)^{-1}\right] \end{gathered}$

(8)

$\boldsymbol{P}_{k+1 \mid k}= \mathit{\boldsymbol{\boldsymbol{\varPhi}}}_{k+1, k} \boldsymbol{P}_{k \mid k} \mathit{\boldsymbol{\boldsymbol{\varPhi}}}_{k+1, k}^{\mathrm{T}}+ \mathit{\boldsymbol{\boldsymbol{\varGamma}}}_k \boldsymbol{Q}_k \mathit{\boldsymbol{\boldsymbol{\varGamma}}}_k^{\mathrm{T}}$

(9)

其中，式(8)中P_k+1|k+1也可写为：

$\boldsymbol{P}_{k+1 \mid k+1}=\left[\boldsymbol{I}-\boldsymbol{K}_{k+1} \boldsymbol{H}_{k+1}\right] \boldsymbol{P}_{k+1 \mid k}$

(10)

综合以上，得到多传感器系统的集中状态估计表达式为：

$\begin{gathered} \hat{\boldsymbol{X}}_{k+1 \mid k+1}=\hat{\boldsymbol{X}}_{k+1 \mid k}+ \\ \sum\limits_{i=1}^N \boldsymbol{K}_{k+1}^i\left[\boldsymbol{Z}_{k+1}^i-\boldsymbol{H}_{k+1}^i \hat{\boldsymbol{X}}_{k+1 \mid k}^i\right] \end{gathered}$

(11)

1.2 分布式滤波器的一种表达形式

根据式(1)和式(2)，与第i个子导航传感器对应的卡尔曼滤波方程为：

$\hat{\boldsymbol{X}}_{k+1 \mid k+1}^i=\hat{\boldsymbol{X}}_{k+1 \mid k}^i+\boldsymbol{K}_{k+1}^i\left[\boldsymbol{Z}_{k+1}^i-\boldsymbol{H}_{k+1}^i \hat{\boldsymbol{X}}_{k+1 \mid k}^i\right]$

(12)

$\boldsymbol{K}_{k+1}^i=\boldsymbol{P}_{k+1 \mid k+1}^i\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^i\right)^{-1}$

(13)

$\begin{gathered} \left(\boldsymbol{P}_{k+1 \mid k+1}^i\right)^{-1}=\left(\boldsymbol{P}_{k+1 \mid k}^i\right)^{-1}+ \\ \left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^i\right)^{-1} \boldsymbol{H}_{k+1}^i \end{gathered}$

(14)

$\hat{\boldsymbol{X}}_{k+1 \mid k}^i= \mathit{\boldsymbol{\boldsymbol{\varPhi}}}_{k+1, k} \hat{\boldsymbol{X}}_{k \mid k}^i$

(15)

$\boldsymbol{P}_{k+1 \mid k}^i= \mathit{\boldsymbol{\boldsymbol{\varPhi}}}_{k+1, k} \boldsymbol{P}_{k \mid k}^i \mathit{\boldsymbol{\boldsymbol{\varPhi}}}_{k+1, k}^{\mathrm{T}}+ \mathit{\boldsymbol{\boldsymbol{\varGamma}}}_k \boldsymbol{Q}_k \mathit{\boldsymbol{\boldsymbol{\varGamma}}}_k^{\mathrm{T}}$

(16)

展开式(5)右边，合并后有：

$\begin{gathered} \hat{\boldsymbol{X}}_{k+1 \mid k+1}= \\ {\left[\boldsymbol{I}-\boldsymbol{K}_{k+1} \boldsymbol{H}_{k+1}\right] \hat{\boldsymbol{X}}_{k+1 \mid k}+\boldsymbol{K}_{k+1} \boldsymbol{Z}_{k+1}} \end{gathered}$

(17)

由式(10)可得：

$\boldsymbol{I}-\boldsymbol{K}_{k+1} \boldsymbol{H}_{k+1}=\boldsymbol{P}_{k+1 \mid k+1} \boldsymbol{P}_{k+1 \mid k}^{-1}$

(18)

从式(12)可推出：

$\begin{gathered} \hat{\boldsymbol{X}}_{k+1 \mid k+1}^i=\left[\boldsymbol{I}-\boldsymbol{P}_{k+1 \mid k+1}^i\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^i\right)^{-1} \boldsymbol{H}_{k+1}^i\right] \\ \hat{\boldsymbol{X}}_{k+1 \mid k}^i+\boldsymbol{P}_{k+1 \mid k+1}^i\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^i\right)^{-1} \boldsymbol{Z}_{k+1}^i \end{gathered}$

(19)

假定所有出现的矩阵的逆矩阵都是存在的，并且P₀为非奇异的。由式(7)可得：

$\begin{gathered} \boldsymbol{K}_{k+1} \boldsymbol{Z}_{k+1}=\boldsymbol{P}_{k+1 \mid k+1} \boldsymbol{H}_{k+1}^{\mathrm{T}} \boldsymbol{R}_{k+1}^{-1} \boldsymbol{Z}_{k+1}= \\ \boldsymbol{P}_{k+1 \mid k+1}\left[\left(\boldsymbol{H}_{k+1}^1\right)^{\mathrm{T}}, \left(\boldsymbol{H}_{k+1}^2\right)^{\mathrm{T}}, \cdots, \left(\boldsymbol{H}_{k+1}^N\right)^{\mathrm{T}}\right] \cdot \\ \operatorname{diag}\left\{\left(\boldsymbol{R}_{k+1}^1\right)^{-1}, \left(\boldsymbol{R}_{k+1}^2\right)^{-1}, \cdots, \left(\boldsymbol{R}_{k+1}^N\right)^{-1}\right\} \cdot \\ {\left[\left(\boldsymbol{Z}_{k+1}^1\right)^{\mathrm{T}}, \left(\boldsymbol{Z}_{k+1}^2\right)^{\mathrm{T}}, \cdots, \left(\boldsymbol{Z}_{k+1}^N\right)^{\mathrm{T}}\right]^{\mathrm{T}}=} \\ \boldsymbol{P}_{k+1 \mid k+1} \sum\limits_{i=1}^N\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^i\right)^{-1} \boldsymbol{Z}_{k+1}^i \end{gathered}$

(20)

对于式(20)中$\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^i\right)^{-1} \boldsymbol{Z}_{k+1}^i$的部分，利用式(19)可得：

$\begin{gathered} \left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^i\right)^{-1} \boldsymbol{Z}_{k+1}^i=\left(\boldsymbol{P}_{k+1 \mid k+1}^i\right)^{-1} \hat{\boldsymbol{X}}_{k+1 \mid k+1}^i- \\ \left(\boldsymbol{P}_{k+1 \mid k+1}^i\right)^{-1}\left[\boldsymbol{I}-\boldsymbol{P}_{k+1 \mid k+1}^i\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}} \cdot\right. \\ \left.\left(\boldsymbol{R}_{k+1}^i\right)^{-1} \boldsymbol{H}_{k+1}^i\right] \hat{\boldsymbol{X}}_{k+1 \mid k}^i \end{gathered}$

(21)

类似于式(18)，有：

$\begin{gathered} \boldsymbol{I}-\boldsymbol{P}_{k+1 \mid k+1}^i\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^i\right)^{-1} \boldsymbol{H}_{k+1}^i= \\ \boldsymbol{P}_{k+1 \mid k+1}^i\left(\boldsymbol{P}_{k+1 \mid k}^i\right)^{-1} \end{gathered}$

(22)

将式(22)代入式(21)：

$\begin{gathered} \left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^i\right)^{-1} \boldsymbol{Z}_{k+1}^i= \\ \left(\boldsymbol{P}_{k+1 \mid k+1}^i\right)^{-1} \hat{\boldsymbol{X}}_{k+1 \mid k+1}^i-\left(\boldsymbol{P}_{k+1 \mid k}^i\right)^{-1} \hat{\boldsymbol{X}}_{k+1 \mid k}^i \end{gathered}$

(23)

将式(18)、(20)、(23)代入式(17)：

$\begin{gathered} \hat{\boldsymbol{X}}_{k+1 \mid k+1}=\boldsymbol{P}_{k+1 \mid k+1}\left\{\boldsymbol{P}_{k+1 \mid k}^{-1} \hat{\boldsymbol{X}}_{k+1 \mid k}+\right. \\ \left.\sum\limits_{i=1}^N\left[\left(\boldsymbol{P}_{k+1 \mid k+1}^i\right)^{-1} \hat{\boldsymbol{X}}_{k+1 \mid k+1}^i-\left(\boldsymbol{P}_{k+1 \mid k}^i\right)^{-1} \hat{\boldsymbol{X}}_{k+1 \mid k}^i\right]\right\} \end{gathered}$

(24)

当式(12)~(16)给出了子滤波器的状态估计时，式(24)代表了N个子导航系统在融合中心的最优估计的表达形式。式(24)中P_k+1|k+1、P_k+1|k、$\hat{\boldsymbol{X}}_{k+1 \mid k}$分别由式(8)、(9)和(6)给出。

对于与第i个子导航传感器对应的子滤波器i，如果在k+1时刻检测到发生故障，则该子滤波器只进行时间更新，即$\hat{\boldsymbol{X}}_{k+1 \mid k+1}^i=\hat{\boldsymbol{X}}_{k+1 \mid k}^i$、P_k+1|k+1ⁱ=P_k+1|kⁱ。此时，根据式(24)，第i个子滤波器不参与系统级的信息融合，进而对第i个子滤波器进行隔离，并自动对系统进行重组^[6]。

以上分析说明，式(24)的分布模型不仅具有集中卡尔曼滤波器的最优特性，同时具有联邦卡尔曼滤波器的较好的容错特性。

1.3 变分贝叶斯原理

当量测噪声方差未知、系统噪声方差已知，包含量测噪声的最优贝叶斯分预测与更新2步^[7-8]。

$\begin{gathered} p\left(\boldsymbol{X}_k, \boldsymbol{R}_k \mid \boldsymbol{Z}_{1: k-1}\right)=\int p\left(\boldsymbol{X}_k \mid \boldsymbol{X}_{k-1}\right) p\left(\boldsymbol{R}_k \mid \boldsymbol{R}_{k-1}\right) \cdot \\ p\left(\boldsymbol{X}_{k-1}, \boldsymbol{R}_{k-1} \mid \boldsymbol{Z}_{1: k-1}\right) \mathrm{d} \boldsymbol{X}_{k-1} \mathrm{~d} \boldsymbol{R}_{k-1} \end{gathered}$

(25)

$\begin{gathered} p\left(\boldsymbol{X}_k, \boldsymbol{R}_k \mid \boldsymbol{Z}_{1: k}\right) \propto \\ p\left(\boldsymbol{Z}_k \mid \boldsymbol{X}_k, \boldsymbol{R}_k\right) p\left(\boldsymbol{X}_k, \boldsymbol{R}_k \mid \boldsymbol{Z}_{1: k-1}\right) \end{gathered}$

(26)

虽然上述贝叶斯滤波是最优的，但后验密度函数在实际中很难求解。变分贝叶斯原理是一种近似方法，对难以求解的后验分布利用多个已知分布进行近似。由变分贝叶斯原理，式(25)和式(26)可转换为如下的高斯分布和逆Gamma分布：

$\begin{gathered} p\left(\boldsymbol{X}_k, \boldsymbol{R}_k \mid \boldsymbol{Z}_{1: k-1}\right)=N\left(\boldsymbol{X}_k \mid \hat{\boldsymbol{X}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right) \cdot \\ \prod\limits_{j=1}^m \operatorname{IG}\left(\sigma_{k, j}^2 \mid \alpha_{k \mid k-1, j}, \beta_{k \mid k-1, j}\right) \end{gathered}$

(27)

$\begin{gathered} p\left(\boldsymbol{X}_k, \boldsymbol{R}_k \mid \boldsymbol{Z}_{1: k}\right)=N\left(\boldsymbol{X}_k \mid \hat{\boldsymbol{X}}_{k \mid k}, \boldsymbol{P}_{k \mid k}\right) \cdot \\ \prod\limits_{j=1}^m \operatorname{IG}\left(\sigma_{k, j}^2 \mid \alpha_{k \mid k, j}, \beta_{k \mid k, j}\right) \end{gathered}$

(28/)

式中，m为量测方差的维数。

将式(25)中的量测噪声方差的预测分布用α_{k|k－1, j}=ρ_jα_{k－1|k－1, j}、β_{k|k－1, j}=ρ_jβ_{k－1|k－1, j}模型作一阶近似，详见文献[9]。其中，ρ_j∈(0, 1]为预测加权系数，σ_{k, j}²为高斯分布的噪声未知方差，α_{k－1|k－1, j}和β_{k－1|k－1, j}为逆Gamma分布的参数。

基于上述分析，第i个子导航传感器对应的自适应卡尔曼滤波的预测过程为：

$\left\{\begin{array}{l} \boldsymbol{\alpha}_{k+1 \mid k}^i=\boldsymbol{\rho}^i \cdot \boldsymbol{\alpha}_{k \mid k}^i \\ \boldsymbol{\beta}_{k+1 \mid k}^i=\boldsymbol{\rho}^i \cdot \boldsymbol{\beta}_{k \mid k}^i \\ \hat{\boldsymbol{X}}_{k+1 \mid k}^i= \mathit{\boldsymbol{\boldsymbol{\varPhi}}}_{k+1, k} \hat{\boldsymbol{X}}_{k \mid k}^i \\ \boldsymbol{P}_{k+1 \mid k}^i= \mathit{\boldsymbol{\boldsymbol{\varPhi}}}_{k+1, k} \boldsymbol{P}_{k \mid k}^i \mathit{\boldsymbol{\boldsymbol{\varPhi}}}_{k+1, k}^{\mathrm{T}}+ \mathit{\boldsymbol{\boldsymbol{\varGamma}}}_k \boldsymbol{Q}_k \mathit{\boldsymbol{\boldsymbol{\varGamma}}}_k^{\mathrm{T}} \end{array}\right.$

(29)

式中，·为点乘运算$\boldsymbol{\rho}^i=\left[\begin{array}{llll} \rho_1^i & \rho_2^i & \cdots & \rho_{m_i}^i \end{array}\right]^{\mathrm{T}}$，$\boldsymbol{\alpha}^i=\left[\begin{array}{llll} \alpha_1^i & \alpha_2^i & \cdots & \alpha_{m_i}^i \end{array}\right]^{\mathrm{T}}$，$\boldsymbol{\beta}^i=\left[\begin{array}{llll} \beta_1^i & \beta_2^i & \cdots & \beta_{m_i}^i \end{array}\right]^{\mathrm{T}}$。

量测更新过程为：

$\left\{\begin{array}{l} \boldsymbol{\alpha}_{k+1 \mid k+1}^i=1 / 2+\boldsymbol{\alpha}_{k+1 \mid k}^i \\ \boldsymbol{\beta}_{k+1 \mid k+1}^{i-}=\boldsymbol{\beta}_{k+1 \mid k}^i \\ \hat{\boldsymbol{R}}_{k+1}^i=\operatorname{diag}\left(\boldsymbol{\beta}_{k+1 \mid k+1}^{i-} \cdot / \boldsymbol{\alpha}_{k+1 \mid k+1}^i\right) \\ \boldsymbol{K}_{k+1}^i=\boldsymbol{P}_{k+1 \mid k}^i\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\left[\boldsymbol{H}_{k+1}^i \boldsymbol{P}_{k+1 \mid k}^i\right. \\ \left.\quad\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}+\hat{\boldsymbol{R}}_{k+1}^i\right]^{-1} \\ \boldsymbol{P}_{k+1 \mid k+1}^i=\left[\boldsymbol{I}-\boldsymbol{K}_{k+1}^i \boldsymbol{H}_{k+1}^i\right] \boldsymbol{P}_{k+1 \mid k}^i \\ \hat{\boldsymbol{X}}_{k+1 \mid k+1}^i=\hat{\boldsymbol{X}}_{k+1 \mid k}^i+\boldsymbol{K}_{k+1}^i\left(\boldsymbol{Z}_{k+1}^i-\right. \\ \left.\quad \boldsymbol{H}_{k+1}^i \hat{\boldsymbol{X}}_{k+1 \mid k}^i\right) \boldsymbol{\beta}_{k+1 \mid k+1}^i=\left(\boldsymbol{Z}_{k+1}^i-\right. \\ \left.\boldsymbol{H}_{k+1}^i \hat{\boldsymbol{X}}_{k+1 \mid k}^i\right) \cdot\left(\boldsymbol{Z}_{k+1}^i-\boldsymbol{H}_{k+1}^i \hat{\boldsymbol{X}}_{k+1 \mid k}^i\right) / 2+ \\ \quad \boldsymbol{\beta}_{k+1 \mid k+1}^{i-}+\operatorname{diag}\left[\boldsymbol{H}_{k+1}^i \boldsymbol{P}_{k+1 \mid k}^i\left(\boldsymbol{H}_{k+1}^i\right)^{\mathrm{T}}\right] / 2 \end{array}\right.$

(30)

式中，·/为点除运算。

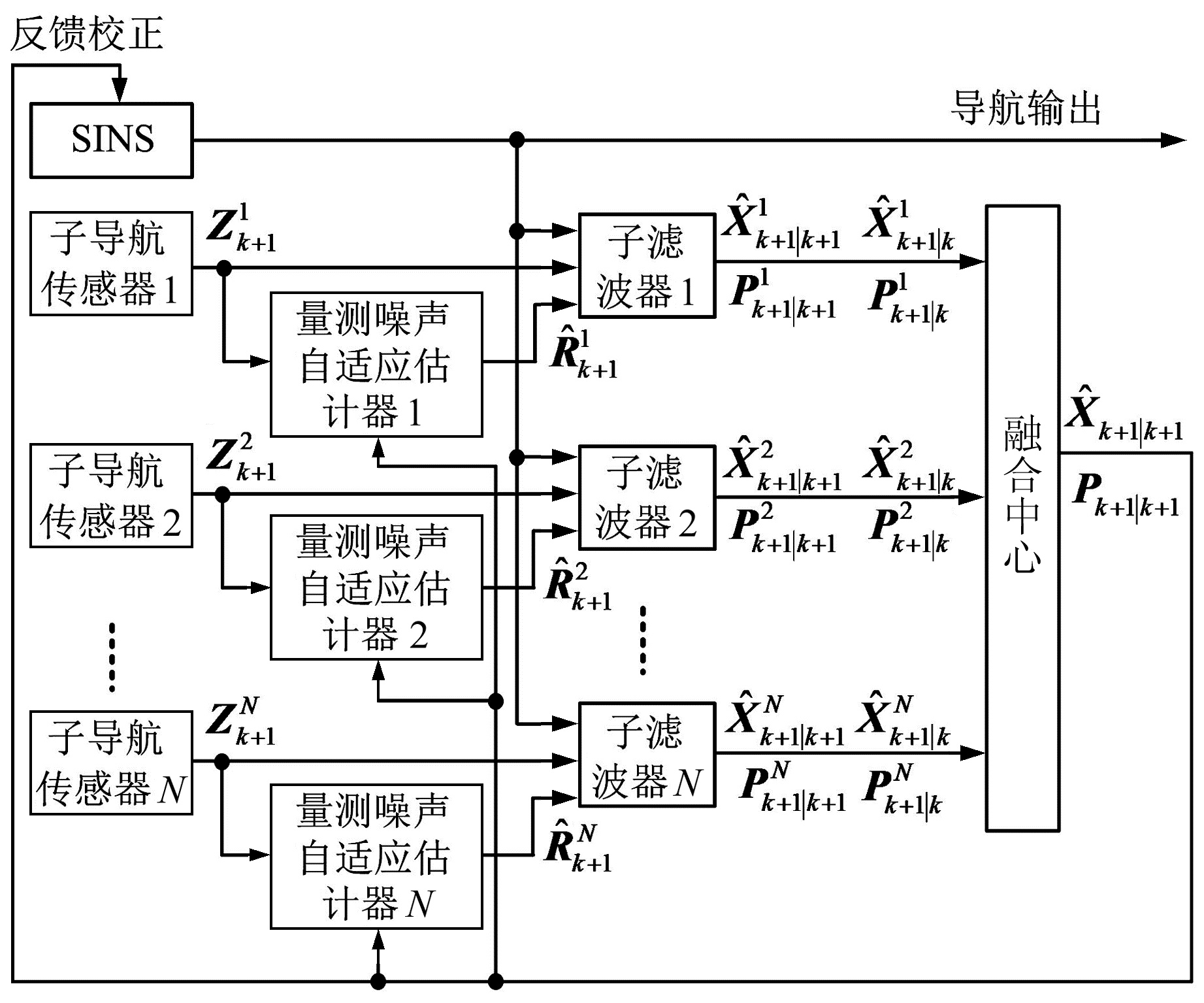
基于式(29)、(30)，利用式(24)可完成多传感器组合导航系统的自适应分布式滤波。从式(29)、(30)看出，量测噪声方差的估计与状态估计相似，也包括预测和更新2个过程，避免了IAE方法中的滑动窗和信息的存储，并可对协方差阵内独立变化的噪声进行单独调整。综上，本文提出的自适应分布式组合导航系统方案见图 1。

2 仿真与分析 2.1 仿真算例模型

以SINS/GNSS/CNS/ADS多传感器组合导航系统为例进行仿真与分析。选取式(1)中的系统状态向量为$\boldsymbol{X}=\left[\varphi_E, \varphi_N, \varphi_U, \delta v_E, \delta v_N, \delta v_U, \delta L, \delta \lambda, \delta h, \varepsilon_{b x}, \varepsilon_{b y}, \varepsilon_{b z}, \varepsilon_{r x}, \varepsilon_{r y}, \varepsilon_{r z}, \nabla_{r x}, \nabla_{r y}, \nabla_{r z}\right]^{\mathrm{T}}$，其中，φ_E、φ_N、φ_U分别为平台东、北、天向的误差角；δv_E、δv_N、δv_U分别为东、北、天向的速度误差；δL、δλ、δh分别为纬度、经度、高度误差；ε_bx、ε_by、ε_bz与ε_rx、ε_ry、ε_rz分别为陀螺沿x、y、z轴的常值漂移误差和一阶Markov漂移误差；$\nabla_{r x}, \nabla_{r y}, \nabla_{r z}$分别为加速度计沿x、y、z轴的一阶Markov漂移误差。

SINS/CNS子系统的量测方程采用姿态组合(转换为地理系下的横滚角、俯仰角、航向角)的模式，SINS/GNSS量测方程采用三维位置及三维速度的组合模式，SINS/ADS量测方程采用高度的组合模式以增强对高度通道的精确测量。

2.2 仿真条件设置

SINS/GNSS/CNS/ADS导航系统的仿真参数设置见表 1。表中，CNS、GNSS和ADS的测量误差均为正常情况下的测量误差，选取仿真时间为3 600 s，SINS的输出速率为100 Hz，GNSS、CNS和ADS的输出速率为1 Hz，量测误差均为高斯噪声。

本文仅考虑量测噪声均方差异常的2种极端情况，即突变和缓变。为此，在GNSS子导航系统的各导航参数中分别加入量测噪声均方差阶跃变化和斜坡变化，而假设CNS及ADS的量测噪声无异常，见表 2，其中，t代表仿真时间。

与GNSS对应的子滤波器中，ρ、α、β的初始值选取为：ρ =[0.99 0.99 0.99 0.99 0.99 0.99]、α = [1 1 1 1 1 1]、β =[2 2 2 0.1 0.1 0.1]。在设定包含起飞、爬升、俯仰、加速、转弯等各种机动飞行轨迹的基础上，针对表 2中GNSS量测噪声均方差异常的2种情况，对算法性能进行仿真分析。

2.3 仿真结果分析

分别对联邦卡尔曼滤波器(FKF)与本文所提的自适应分布式滤波(ADK F)算法进行仿真实验。其中，FKF方法采用基于残差卡方检测的、具有容错功能的、带有重置式的信息融合模式。

图 2为当GNSS量测噪声均方差发生突变时2种方法的仿真结果。可以看出，当GNSS量测噪声均方差突变时，FKF算法的滤波精度非常差，主要原因是其相关子滤波器在处理GNSS时得到的故障检测结果大于门限值，此时认为与GNSS相连的子滤波器发生故障进而进行隔离。因为组合导航系统引入了ADS，增加了高度通道的可观测性，故其高度与天向速度的精度较好。

图 3为利用ADKF算法对GNSS量测噪声均方差发生突变时的跟踪曲线。可以看出，ADKF算法能够较为准确地跟踪GNSS量测噪声均方差的变化，进而提高组合导航系统的滤波精度。

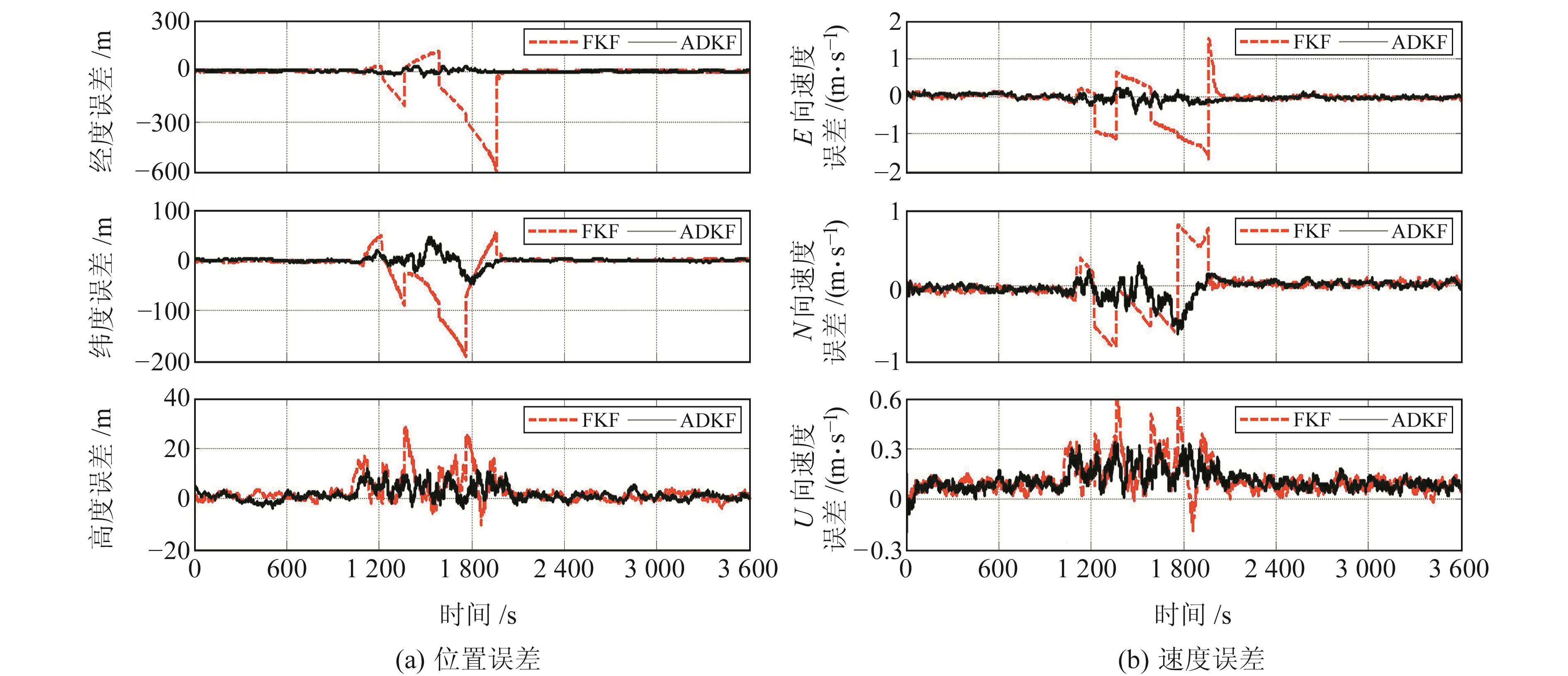
图 4为当GNSS量测噪声均方差发生缓变时2种方法的仿真结果，图 5为利用ADKF算法对GNSS量测噪声均方差发生缓变时的跟踪曲线。图 4、5进一步证明了本文算法在处理量测噪声均方差发生变化时的优越性。

3 结语

本文提出组合导航系统的自适应分布式滤波算法以提高组合导航系统在量测噪声统计特性异常时的滤波精度。首先给出一种分布式滤波的表达形式，以便于故障的自动隔离及系统的自动重组，然后结合变分贝叶斯估计理论以自适应调整量测噪声的方差。仿真结果表明，本文算法能有效跟踪量测噪声方差的变化，提高组合导航系统的精度。

本文仿真分析仅考虑了GNSS量测噪声方差发生变化的情况，对于其他子导航传感器或多个子导航传感器的量测噪声方差发生变化的情况，本文算法也同样适用。