2. 南京理工大学自动化学院,南京市孝陵卫街200号,210094;
3. 金陵科技学院智能科学与控制工程学院,南京市弘景大道99号,211169
随着多卫星导航系统的发展[1-2],很容易出现多个观测值同时出现粗差的现象[3-4]。处理策略分为两类,一类将粗差归纳为函数模型进行探测和剔除[5]。接收机自主完好性监测(receiver autonomous integrity monitoring, RAIM)被认为是对抗非故意干扰和故意攻击的有效对策,不仅可用于检测粗差,而且排除粗差后能提供精确的位置、速度和时间解。在处理由有意或无意行为引起的多个粗差时,RAIM FDE方法通常通过迭代搜索来排除潜在粗差[6],效率较低。另一类方法是将粗差归纳为随机模型,采用基于稳健统计的估计方法减少伪距测量不准确带来的影响[7]。
为弥补GNSS信号可用性的局限性所造成的缺陷,可利用惯性传感器辅助进行组合定位[8]。卡尔曼滤波是目前最实用的实时最优估计方法,但当模型误差具有时变特征时,很难获得所需的信息,不适当的统计信息和异常值会降低其性能,甚至可能导致滤波发散,特别是当信号退化时,环境中的复杂扰动会导致观测值异常。为消除异常值的影响,可使用控制卡尔曼滤波质量的方法,如检测、识别和自适应方法[9]。但当测量值包含多个异常值时,检测和识别过程难以实现。
基于以上研究,本文提出一种惯性辅助的FDE方法,将惯性的状态模型和测量模型信息引入RAIM,构造检验统计量,有效解决错误剔除粗差和未完全剔除粗差的问题。最后,利用仿真实验对传统FDE方法与改进方法的误判率和漏检率进行比较分析。
1 粗差检测和识别的数学模型在惯性辅助的卫星组合导航系统中,将状态模型和测量模型的信息引入RAIM,在卡尔曼滤波方程中将预测状态
| $ \boldsymbol{L}_k=\boldsymbol{A}_k \hat{\boldsymbol{X}}_k+\boldsymbol{V}_k $ | (1) |
式中,Lk为观测向量,Ak为设计矩阵,Vk为残差向量,且
| $ \left\{\begin{array}{l} \boldsymbol{L}_k=\left[\begin{array}{ll} \boldsymbol{z}_k & \tilde{\boldsymbol{x}}_k \end{array}\right] \\ \boldsymbol{A}_k=\left[\begin{array}{ll} \boldsymbol{H}_k & \boldsymbol{I} \end{array}\right] \\ \boldsymbol{V}_k=\left[\begin{array}{ll} \boldsymbol{v}_{z k} & \boldsymbol{v}_{x k} \end{array}\right] \\ \boldsymbol{C}_{L_k}=\left[\begin{array}{llll} \boldsymbol{R}_k & \mathbf{0} & \mathbf{0} & \widetilde{\boldsymbol{P}}_k \end{array}\right] \end{array}\right. $ |
式中,Hk为观测矩阵,I为单位矩阵,vzk为观测值残差向量,vxk为预测状态的残差向量,CLk为方差协方差矩阵,Rk为观测值方差阵,
| $ \left\{\begin{array}{l} \hat{\boldsymbol{X}}_k=\left(\boldsymbol{A}_k^{\mathrm{T}} \boldsymbol{C}_{L_k}^{-1} \boldsymbol{A}_k\right)^{-1} \boldsymbol{A}_k^{\mathrm{T}} \boldsymbol{C}_{L_k}^{-1} \boldsymbol{L}_k \\ \boldsymbol{Q}_{\hat X_k}=\left(\boldsymbol{A}_k^{\mathrm{T}} \boldsymbol{C}_{L_k}^{-1} \boldsymbol{A}_k\right)^{-1} \end{array}\right. $ | (2) |
与之对应的估计残差和其协方差矩阵为:
| $ \left\{\begin{array}{l} \boldsymbol{V}_k=\boldsymbol{A}_k \hat{\boldsymbol{X}}_k-\boldsymbol{L}_k \\ \boldsymbol{Q}_{V_k}=\boldsymbol{C}_{L_k}-\boldsymbol{A}_k \boldsymbol{Q}_{\hat{X}_k} \boldsymbol{A}_k^{\mathrm{T}} \end{array}\right. $ | (3) |
粗差检测检验是一种二元假设检验,根据残差及其协方差矩阵进行全局检验,构建方差因子统计量Tk[10]:
| $ T_k=\boldsymbol{V}_k^{\mathrm{T}} \boldsymbol{C}_{L_k}^{-1} \boldsymbol{V}_k $ | (4) |
当统计量Tk服从自由度为m-4的χ2分布时,无粗差;一旦出现粗差,统计量就会服从自由度为m-4的非中心χ2分布。在显著水平的情况下,当Tk>χm-42(α)时,判定存在粗差;当统计量低于阈值时,则认为观测值是可信的。
利用数据探测法进行局部检验,并通过统计量的大小进行粗差识别,第i个观测量的检验统计量为[10]:
| $ w_i=\left|\boldsymbol{e}_i^{\mathrm{T}} \boldsymbol{C}_{L_k}^{-1} \boldsymbol{v}_k\right| / \sqrt{\boldsymbol{e}_i^{\mathrm{T}} \boldsymbol{C}_{L_k}^{-1} \boldsymbol{Q}_{V_k} \boldsymbol{C}_{L_k}^{-1} \boldsymbol{e}_i} $ | (5) |
式中,ei=[0···1···0]T为第i个元素为1、其他元素为0的单位向量。当该观测值上无粗差时,wi~N(0, 1),检验统计量wi≤μ1-α/2,其中,μ1-α/2为显著水平对应的标准正态分布的分位值;反之,则存在粗差。本文设显著水平α=0.1%,其对应的阈值为3.291。
2 实验与分析搭建惯性辅助卫星的紧组合数学仿真平台,对所提出的改进的FDE方法进行验证。陀螺常值零偏和白噪声分别为5°/h和0.035°/
当粗差检测函数告警时,进行GNSS粗差值排除,此时可能存在单个粗差或多个粗差。对于排除粗差有一系列的替代假设,每一个卫星都与当前历元全部观测值构成的一个子集相关联,该子集根据相关的假设检验将卫星标记为粗差/健康。图 1提供了各种情况的示例,表 1为卫星粗差检测和剔除可能出现的4种方案。

|
图 1 异常观测值示例 Fig. 1 Examples of anomalous observations |
|
|
表 1 粗差检测和剔除的类型 Tab. 1 Gross errors detection and elimination types |
为了验证粗差检测的效果,在第1~4 476 s中分别对第2、5和7个观测值加入10 m的阶跃粗差。其中,100、2 028、2 983和3 038等4个历元分别解算出了所对应的4种方案结果。以方案①为例,表 2给出FDE方法粗差检验统计量和剔除情况。表 3给出4种方案对应4个历元的定位结果。由表可知,方案①剔除粗差后结果最优;方案②~④剔除粗差后,定位精度反而不如保留粗差时高,说明误判和漏检都会对定位性能造成影响。
|
|
表 2 FDE方法GNSS粗差检验统计量(100历元) Tab. 2 GNSS gross errors test statistics of FDE method(100 epoch) |
|
|
表 3 FDE方法GNSS定位误差 Tab. 3 GNSS positioning error of FDE method |
方案①依次识别了第7、5和2个观测值上存在粗差,对应的检验统计量分别为9.187、8.528和6.261(表 2中加粗字体),超过了门限阈值3.291。该历元剔除了所有粗差卫星,同时也保留了所有健康卫星。由表 3可知,方案①的定位精度最高。
方案②分别检测出第7、1、13、2和5等5个观测值上存在粗差。该历元剔除了1和13两个健康观测值,同时也剔除了7、5和2三个粗差观测值。由表 3可知,该历元虽然能够完全正确剔除所有粗差卫星,但同时也去除了2颗健康卫星,造成定位性能有所降低。方案③分别检测出了2和3两个观测值上存在粗差。该历元剔除了1个健康观测值和1个粗差观测值,同时有2个粗差观测值未能检测出。由表 3可知,该历元不仅保留了粗差卫星,而且剔除了健康卫星观测值,使得定位精度严重下降。方案④分别检测出2和5两个观测值上存在粗差。该历元剔除了2个粗差卫星,有1个粗差卫星未能检测出。由表 3可知,该历元剔除粗差后的精度相较于保留粗差时要差。
使用惯性辅助FDE方法时,方案①~④的4个历元都能正确检测出粗差的数量和位置。以方案①为例,表 4为对应历元的局部检验统计量,其正确检测出第2、5和7个观测值上存在粗差。表 5为使用惯性辅助FDE方法时的定位误差,与表 3相比,其定位精度显著更优。
|
|
表 4 惯性辅助的FDE方法GNSS粗差检验统计量(100历元) Tab. 4 GNSS gross errors test statistics of inertial-aided FDE method (100 epoch) |
|
|
表 5 惯性辅助的FDE方法GNSS定位误差 Tab. 5 GNSS positioning error of inertial-aided FDE method |
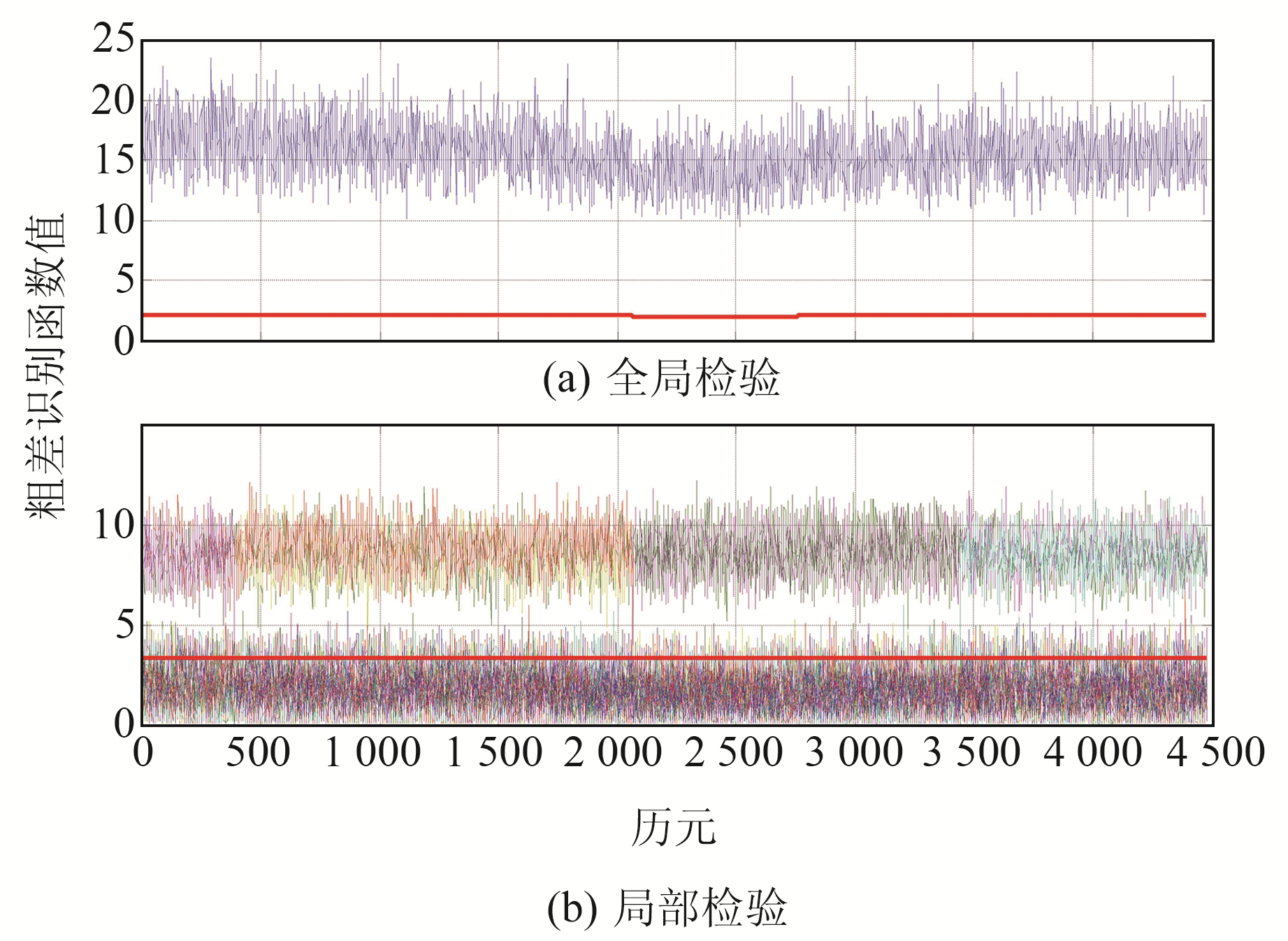
图 2、3分别为每个历元加入3个10 m粗差后FDE方法和惯性辅助的FDE方法各个历元的全局检验量和局部检验量。由图可知,所有历元全局检验量都超过门限阈值,都能检测出粗差,而惯性辅助的FDE方法的粗差识别函数值相较于FDE方法更稳定,更易准确识别粗差。

|
图 2 FDE方法GNSS粗差探测和识别函数值 Fig. 2 GNSS gross errors detection and identification function values of FDE method |
|
图 3 惯性辅助的FDE方法GNSS粗差探测和识别函数值 Fig. 3 GNSS gross errors detection and identification function values of inertial-aided FDE method |
图 4为FDE方法识别的粗差数量。由图可知,大部分历元可以识别3个粗差;个别历元漏检了粗差,仅识别出1~2个粗差;部分历元误判了粗差,识别出4~5个粗差。

|
图 4 FDE方法粗差识别数量 Fig. 4 The number of gross errors detected by FDE method |
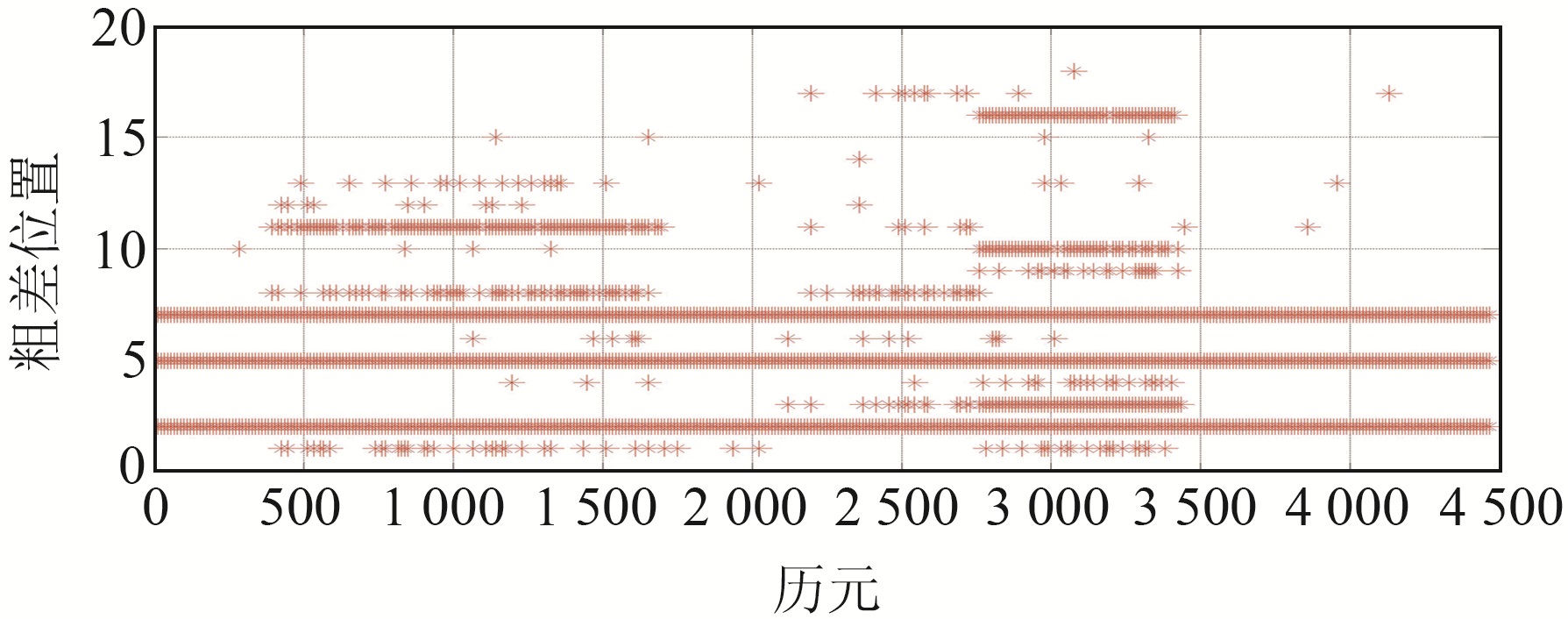
图 5为FDE方法探测的粗差位置,实际的粗差加入在第2、5和7三个观测值中。从图中可明显看出,多个历元健康的观测值被认为是粗差,误判的情况明显。
|
图 5 FDE方法探测的粗差位置 Fig. 5 Gross errors location detected by FDE method |
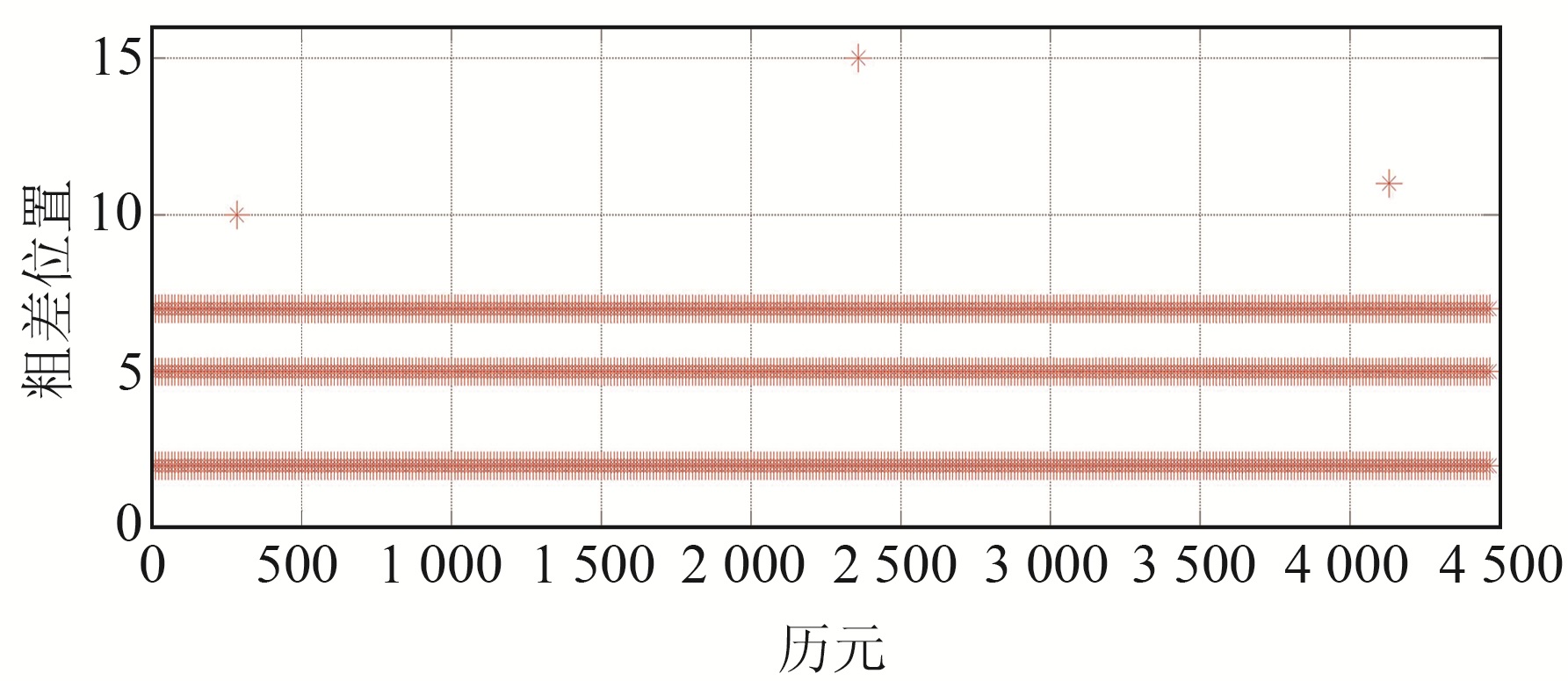
图 6、7分别为惯性辅助的FDE方法识别粗差的数量和位置。由图 6可知,几乎所有历元都能识别3个粗差,仅有3个历元有误判的情况,且没有漏检的存在。由图 7可知,分别在第286、2 359和4 136历元将第10、15和11个健康观测值识别为粗差。

|
图 6 惯性辅助的FDE方法粗差识别数量 Fig. 6 The number of gross errors detected by inertial-aided FDE method |
|
图 7 惯性辅助的FDE方法探测的粗差位置 Fig. 7 Gross errors location detected by inertial-aided FDE method |
图 8、9分别为FDE方法和惯性辅助的FDE方法剔除粗差和保留粗差的定位结果,表 6为定位结果统计。由图 8可见,由于方案②~④不能完全正确剔除粗差,使得传统的FDE方法定位结果不是最优的。在500~1 500和2 500~3 500历元阶段,剔除粗差后的精度明显低于保留粗差的结果;其他时间段可以正确识别粗差,剔除粗差后的精度优于保留粗差的结果。由图 9可见,使用惯性辅助的FDE方法时,所有历元中仅有3个观测值存在误判的情况,无漏检的情况存在,剔除粗差后,定位精度稳定。相较于FDE方法剔除粗差和保留粗差的情况,惯性辅助的FDE方法定位精度分别提高87.36%和86.47%。

|
图 8 FDE方法定位误差 Fig. 8 Positioning error of FDE method |

|
图 9 惯性辅助的FDE方法定位误差 Fig. 9 Positioning error of inertial-aided FDE method |
|
|
表 6 定位误差统计 Tab. 6 Statistics of positioning error |
当观测值中存在不同数量的粗差时,对比分析传统的FDE方法和惯性辅助的FDE方法的效果。每个历元分别加入1、2、3、4个10 m的粗差,表 7为4种情况下误判率和漏检率统计结果。当加入1个和2个粗差时,FDE方法误检和漏检率都很低,粗差检测和剔除效果好;当加入3个和4个粗差时,FDE方法检测的误判率分别为8.445% 和9.869%,漏检率分别为5.950%和8.568%,定位性能低。而惯性辅助的FDE方法能够显著改善2个以上粗差的检测效能,漏检率和误检率都显著降低。
|
|
表 7 加入10 m粗差的误检和漏检率 Tab. 7 False and missed detection rate with 10 m gross errors |
图 10为加入10 m、15 m和20 m粗差时FDE方法的识别数量情况。可以看出,随着粗差变大,加入20 m粗差时,FDE方法最多识别8个粗差,多剔除了5个观测值。这是由于观测值之间存在相关性,粗差增大时影响其余的观测值,使得误判概率变大,导致定位性能降低。

|
图 10 FDE方法粗差识别数量 Fig. 10 The number of gross errors detected by FDE method |
表 8为不同大小的粗差误检和漏检率统计结果,共4 476个历元,每个历元加入3个粗差,共加入13 428个粗差。由表可知,随着误差增大,FDE方法的误判率逐渐增大,漏检率减小。使用惯性辅助时,对于不同大小的粗差,误检和漏检的概率一致,说明随着粗差的增大,惯性辅助的FDE方法能够有效识别不同大小的粗差,显著改善误判和漏检的概率。
|
|
表 8 误检和漏检率 Tab. 8 False and missed detection rate |
本文提出一种惯性辅助的多粗差检测和排除方法,可有效降低多个粗差对定位精度的影响。通过计算分析,主要得出如下结论:
1) 当观测值中存在多个粗差时,传统的FDE方法易出现错误剔除粗差和未完全剔除粗差的情况,导致定位性能降低。
2) 当观测值中存在2个以上粗差时,传统的FDE方法误判率和漏检率随着粗差数量的增加而增大,且随着粗差增大,误判率也会增大;通过惯性辅助能显著提升多粗差探测的效率,降低误检和漏检概率,提高组合导航定位的性能。
| [1] |
舒宝, 义琛, 王利, 等. 华为P30手机GPS/BDS/GLONASS/Galileo观测值随机模型优化及定位性能分析[J]. 大地测量与地球动力学, 2022, 42(12): 1222-1226 (Shu Bao, Yi Chen, Wang Li, et al. Improvement of Stochastic Model and Positioning Performance Analysis of GPS/BDS/GLONASS/Galileo Observations of Huawei P30 Smartphone[J]. Journal of Geodesy and Geodynamics, 2022, 42(12): 1222-1226)
(  0) 0) |
| [2] |
Angrisano A, Gaglione S, Crocetto N, et al. PANG-NAV: A Tool for Processing GNSS Measurements in SPP, Including RAIM Functionality[J]. GPS Solutions, 2019, 24(1): 1-7
(  0) 0) |
| [3] |
Wu Y L, Chen S, Yin T T. GNSS/INS Tightly Coupled Navigation with Robust Adaptive Extended Kalman Filter[J]. International Journal ofAutomotive Technology, 2022, 23(6): 1639-1649 DOI:10.1007/s12239-022-0142-7
(  0) 0) |
| [4] |
张倩倩, 归庆明, 宫轶松. 卫星多故障探测和识别的独立分量分析法[J]. 测绘学报, 2017, 46(6): 698-705 (Zhang Qianqian, Gui Qingming, Gong Yisong. Multiple Satellite Faults Detection and Identification Based on the Independent Component Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(6): 698-705)
(  0) 0) |
| [5] |
刘一, 谷守周, 边少锋, 等. 一种基于观测数据集密度中心的新型RAIM算法[J]. 武汉大学学报: 信息科学版, 2021, 46(12): 1900-1906 (Liu Yi, Gu Shouzhou, Bian Shaofeng, et al. A New RAIM Algorithm Based on the Density Center of Observed Dataset[J]. Geomatics and Information Science of Wuhan University, 2021, 46(12): 1900-1906)
(  0) 0) |
| [6] |
Zhang K W, Papadimitratos P. Fast Multiple Fault Detection and Exclusion(FM-FDE) Algorithm for Standalone GNSS Receivers[J]. IEEE Open Journal of the Communications Society, 2021(2): 217-234
(  0) 0) |
| [7] |
Tan T N, Khenchaf A, Comblet F, et al. Robust-Extended Kalman Filter and Long Short-Term Memory Combination to Enhance the Quality of Single Point Positioning[J]. Applied Sciences, 2020, 10(12): 4335 DOI:10.3390/app10124335
(  0) 0) |
| [8] |
Jiang C, Zhang S B, Zhang Q Z. Adaptive Estimation of Multiple Fading Factors for GPS/INS Integrated Navigation Systems[J]. Sensors, 2017, 17(6): 1254 DOI:10.3390/s17061254
(  0) 0) |
| [9] |
Wang S Z, Zhan X Q, Zhai Y W, et al. Fault Detection and Exclusion for Tightly Coupled GNSS/INS System Considering Fault in State Prediction[J]. Sensors, 2020, 20(3): 590
(  0) 0) |
| [10] |
Jiang C, Zhang S B, Cao Y Z, et al. A Robust Fault Detection Algorithm for the GNSS/INS Integrated Navigation Systems[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 12-24
(  0) 0) |
2. School of Automation, Nanjing University of Science and Technology, 200 Xiaolingwei Street, Nanjing 210094, China;
3. College of Intelligent Science and Control Engineering, Jinling Institute of Technology, 99 Hongjing Road, Nanjing 211169, China
 2023, Vol. 43
2023, Vol. 43

