2. 福建省地震台,福州市华鸿路7号,35000;
3. 中国地震局第一监测中心,天津市耐火路7号,300180
在沿海和岛屿区域进行微重力观测须考虑海潮的影响[1-3]。由于近岸浅水区的潮汐运动较复杂,现有的海潮模型在海岸线附近精度均较低[4],特别是相位误差较大,须用验潮数据进行修正[5]。
由于连续重力台站较少,难以对漫长的海岸线进行有效控制,利用便携式相对重力仪布设流动测站是目前最为经济可行的观测方式。但与固定台连续重力仪相比,便携式相对重力仪的零漂率较大且非线性较强,非线性零漂难以完全校正,在计算调和常数时可能引入较大误差。有学者将Burris重力仪用于重力潮汐观测实验[6-7],但对于国内装备数量更多的CG型重力仪(CG-5、CG-6)只有定性讨论,没有定量分析。为此,在厦门地震台测试CG型重力仪在潮汐频段的噪声,用长期观测的gPhone型连续重力仪数据建立测站潮汐模型,预测出同址对比测试时段的海潮负荷值,将海潮负荷值作为已知量,分离得到gPhone、CG-5、CG-6的残差时间序列,并进行频谱分析,检查这3种仪器的非线性漂移在潮汐频段的量级。
1 CG型重力仪的适用性实验实验地厦门地震台离海岸线约700 m,gPhone重力仪(SN: 056)安装在山体洞室内,采样间隔为1 s,CG-5(SN: 1 316)和CG-6(SN: 414)重力仪置于地面办公楼内,采样间隔分别为44 s和60 s。用于对比的数据时段为2022-11-16~22。使用Tsoft程序[8]进行数据预处理,首先统一采样率至60 s,对地震造成的突跳、台阶等进行处理,然后进行固体潮、气压和线性漂移改正(图 1)。
|
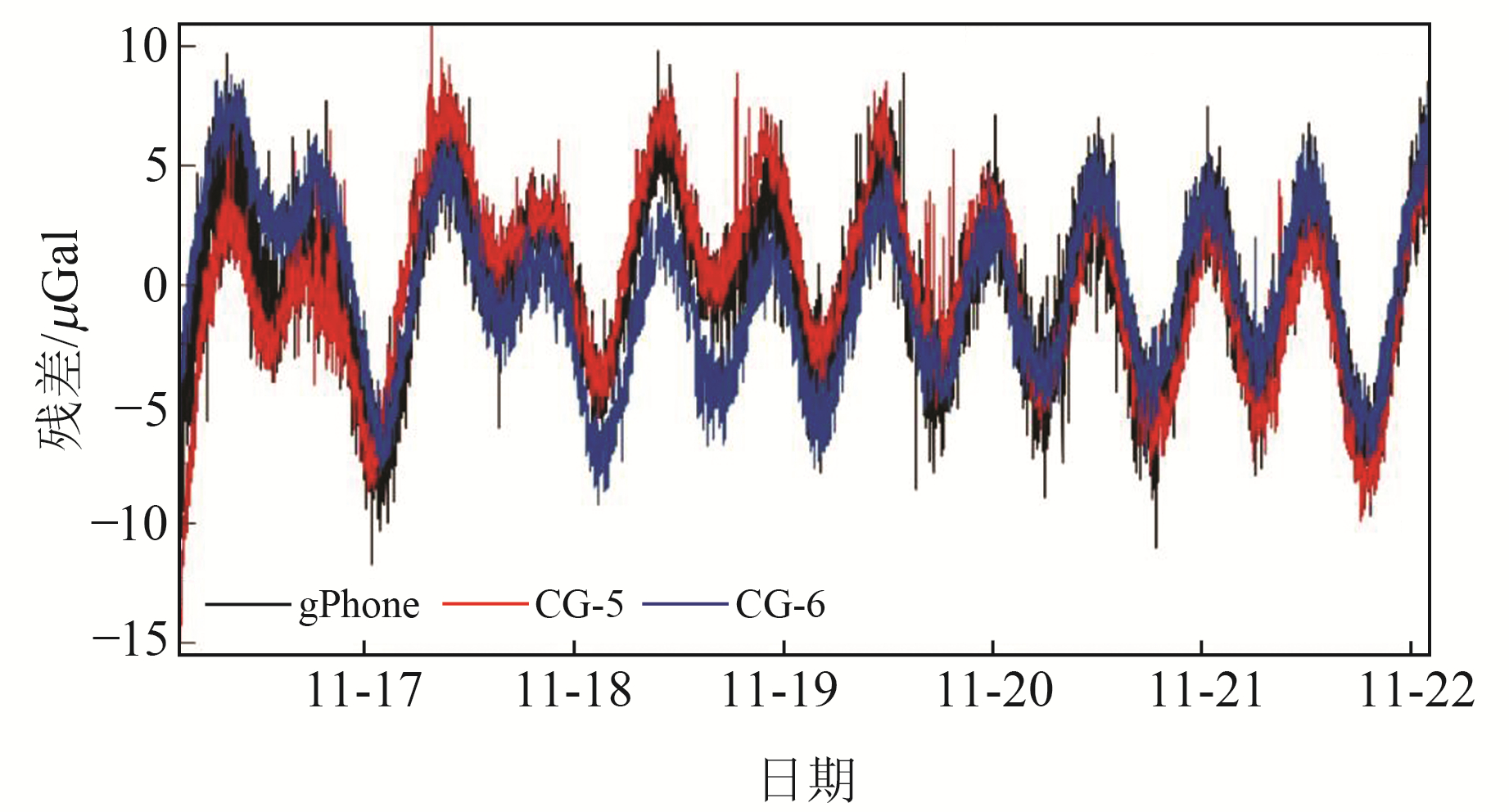
图 1 海潮改正前的gPhone、CG-5、CG-6重力仪观测残差 Fig. 1 The observation residuals of gPhone, CG-5 and CG-6 gravimeters before tidal correction |
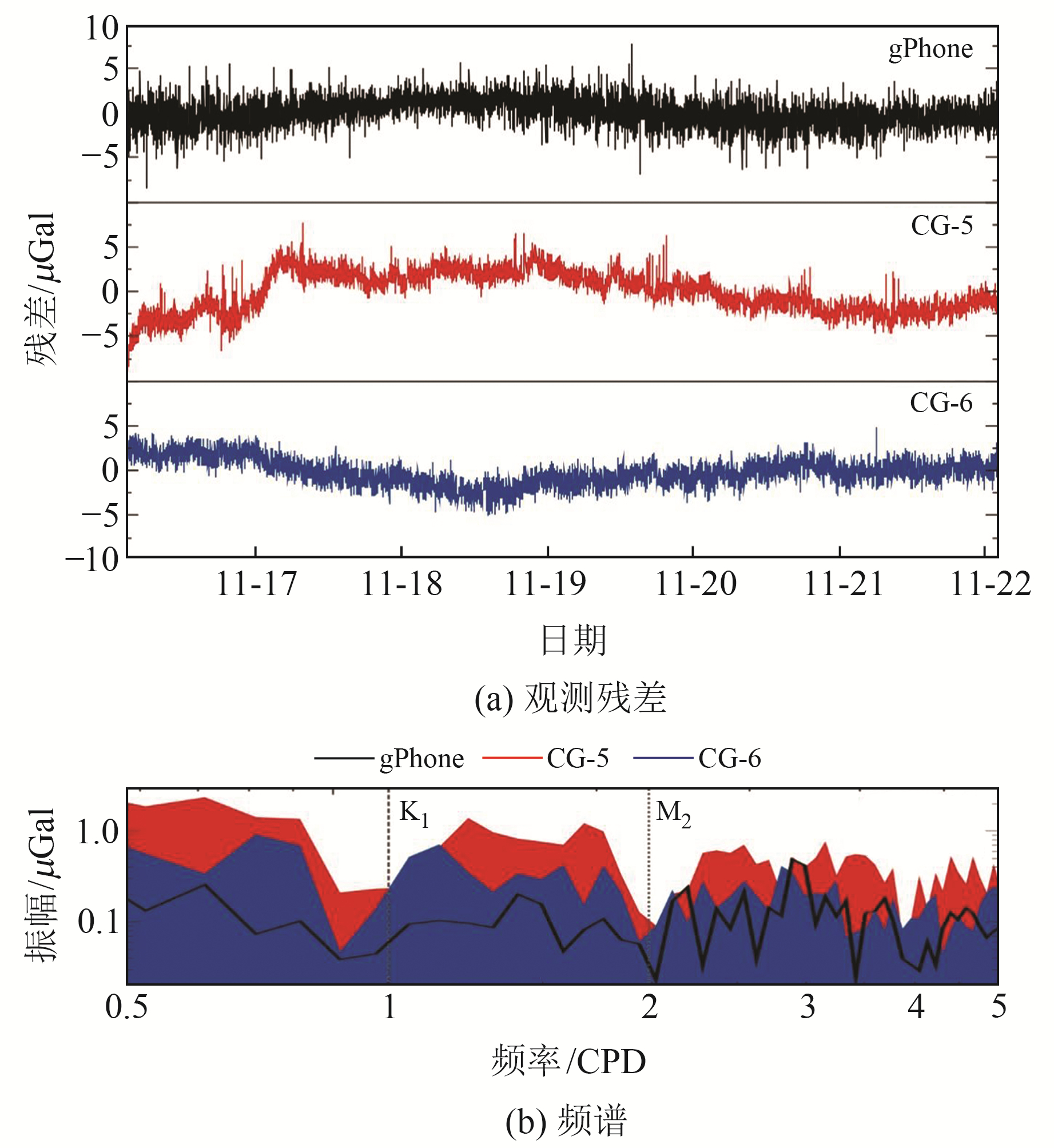
选择在厦门台适用性较好的FES2004海潮模型[9-10],应用Venedikov调和分析方法分析gPhone在2017-03-01~2021-03-01的观测数据,修正得到测站海潮模型,用SPOTL程序[11]计算同址对比测试时段的重力海潮负荷改正值,并应用于这3台仪器的观测数据,得到精确海潮改正后的残差时间序列(图 2(a))。可以看出,gPhone在地震频段的噪声水平显著高于CG-5和CG-6,这是由于厦门台的地脉动噪声较强[12],而CG-5和CG-6数据的卡尔曼滤波对高频噪声的抑制比gPhone数据的最小二乘滤波更好。
|
图 2 海潮改正后的观测残差及频谱 Fig. 2 The observation residuals and amplitude spectrums after ocean tidal correction |
由于海潮主要的8个分潮(振幅最大的4个半日分潮M2、S2、N2、K2和4个全日分潮K1、O1、P1、Q1)的频率分别集中在2 CPD和1 CPD附近,而实际测量中单个测点(绝对)或测段(相对)的观测大多在2~3 d之内完成,所以对重力观测精度影响最大的频率成分在2 CPD和1 CPD附近。因此,对残差时间序列作傅里叶变换,将0.5~5 CPD间的振幅谱绘制成图 2(b)。可以看出,总体上gPhone的残差振幅最小,CG-6次之,CG-5最大。CG-6在2~5 CPD频段内振幅与gPhone相当,0.5~2 CPD频段内振幅介于gPhone和CG-5之间。从时间域来看,3种仪器的非线性漂移皆不相关,可排除大气负荷或风暴潮等因素的影响,漂移特性的差异可能源于仪器内部温度控制性能。此次实验中办公楼内的温度波动显著大于山体洞室,在野外工作实践中发现,CG-5读数对环境温度的变化较为敏感,而CG-6由于内温较高(60℃)且温度控制系统的灵敏度较高,受环境温度的影响较小。在关键的1.9 CPD和1.0 CPD频率点附近,残差振幅最大的CG-5约为0.5 μGal和1.0 μGal,而厦门台的海潮负荷约为7.5 μGal,因此可认为CG-5的非线性漂移(自噪声水平)对短时潮汐观测影响较小,数据可满足主要的半日分潮和全日分潮分析需要。
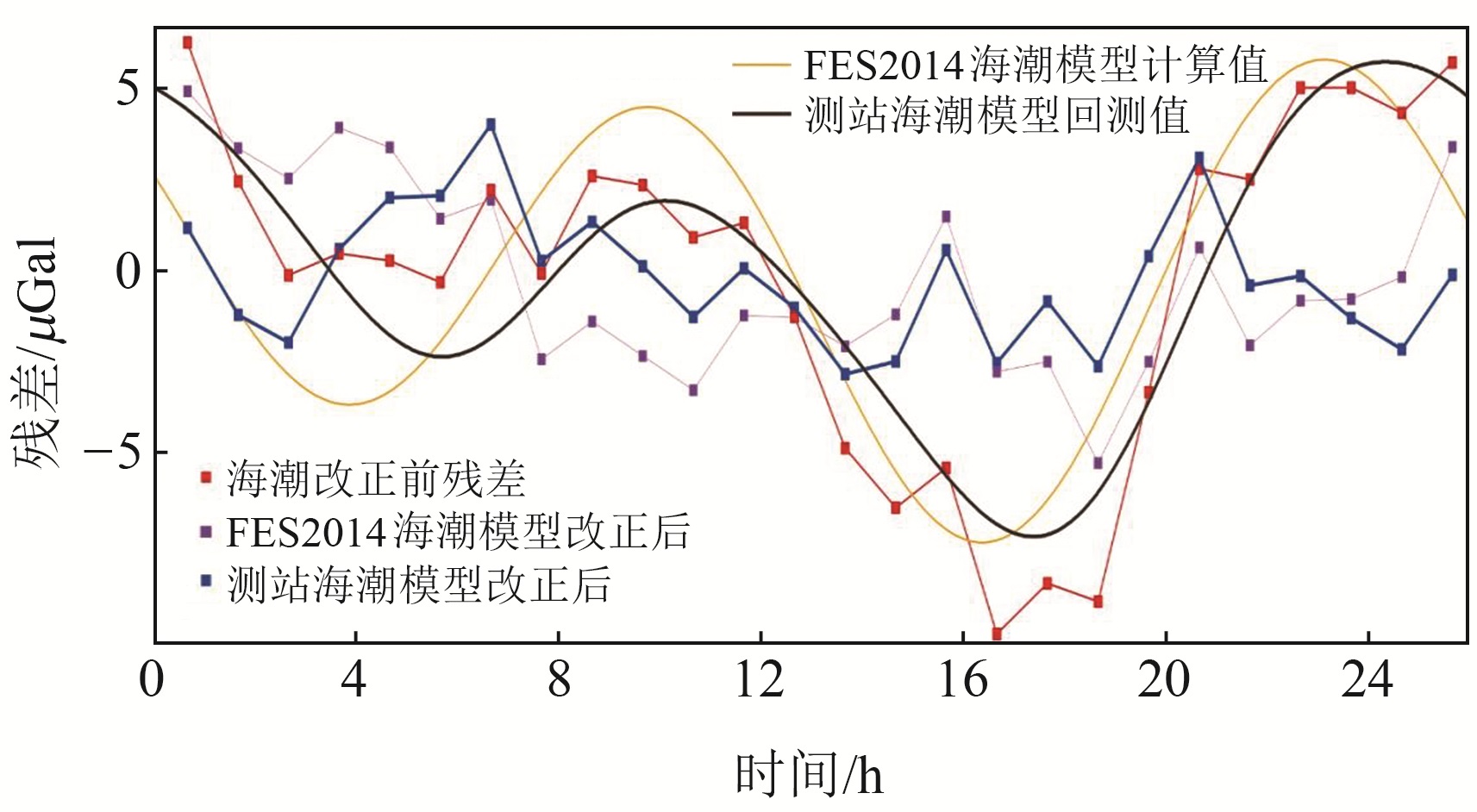
2 平潭岛的海潮改正实验2022-08-21~22中国地震局第一监测中心使用A-10型绝对重力仪在平潭岛进行绝对重力测量,发现虽然该测点离海岸线超过3 km,且观测时段为小潮,但仍受到较大的海潮影响。由于该测点尚未部署连续重力仪,因此使用CG-5型重力仪在2022-09-26~30进行88 h的重力潮汐观测,利用此次观测数据修正对平潭岛适应性较好的FES2014海潮模型[13-14],得到测站海潮模型,并回测绝对重力观测时段的海潮负荷值。海潮改正前后的绝对重力组均值残差序列见图 3。可以看出,改正前残差波动较大,标准差为4.8 μGal,其时间序列与FES2014海潮模型的形态和相位均有一定差异,改正后标准差为2.7 μGal;测站海潮模型回测值与海潮改正前残差较为符合,改正后标准差减小至1.8 μGal。由此可见,测站海潮模型精度较FES2014海潮模型大幅提高,验证了利用CG-5型重力仪的短时潮汐观测数据提取海潮调和常数的可靠性。
|
图 3 海潮改正前后平潭岛绝对重力观测残差序列 Fig. 3 Residual sequences of absolute gravity observation before and after ocean tide correction at Pingtan island |
通过同址对比测试得出,目前常用的CG型便携式重力仪静态观测时在1 CPD和2 CPD附近的噪声水平较低,满足主要的全日分潮和半日分潮的调和常数计算的需要。在平潭岛的实际应用证明,即使是使用非线性漂移较大的CG-5进行短时重力潮汐观测,仍能建立较高精度的测站海潮模型,回测35 d前的海潮负荷值与绝对重力观测组均值残差序列符合较好,改正效果较FES2014海潮模型有较大提升,由此验证了CG型重力仪用于海潮负荷观测的可行性与有效性。
利用便携式重力仪进行海潮负荷观测时应注意以下2点:1) CG-5在环境温度不稳定的临时测站中可能出现较大的非线性漂移,应尽可能使用漂移特性更好的CG-6。由于CG型重力仪的非线性漂移幅值较大,应通过最小二乘法建立法方程来修正海潮模型,不可直接将读数变化视作海潮负荷。2) 海洋潮汐除了主要的全日分潮和半日分潮外,还包括一些长周期潮波;另外,大气负荷和风暴同样可能引起较强的振幅,所以利用短时潮汐观测数据修正的海潮模型仍有一定的误差。因此在海岸线附近进行微重力观测时,宜同步进行重力潮汐观测。
下一步可尝试在测站环境温度控制较好的条件下,使用CG-6作较长时间(28 d以上)的重力潮汐观测,分析其用于提取长周期潮波的可行性。
| [1] |
纪立东, 张权, 张宏伟, 等. 潮汐对高精度重力测量的改正分析[J]. 测绘地理信息, 2014, 39(1): 26-28 (Ji Lidong, Zhang Quan, Zhang Hongwei, et al. On the Tide Correction of Hige-Precision Gravity Measurements[J]. Journal of Geomatics, 2014, 39(1): 26-28)
(  0) 0) |
| [2] |
邓洪涛, 赵珞成. 海岛重力测量负荷改正及其影响因素分析[J]. 海洋测绘, 2017, 37(1): 14-16 (Deng Hongtao, Zhao Luocheng. Load Correction of Island Gravity Survey and Its Influence Factors[J]. Hydrographic Surveying and Charting, 2017, 37(1): 14-16)
(  0) 0) |
| [3] |
杜文成, 袁林果, 张宁宁, 等. 青岛台站重力固体潮和海潮负荷特征研究[J]. 大地测量与地球动力学, 2018, 38(9): 913-916 (Du Wencheng, Yuan Linguo, Zhang Ningning, et al. Study of Earth' s Gravity Tide and Oceanic Loading Characteristics at Qingdao Station[J]. Journal of Geodesy and Geodynamics, 2018, 38(9): 913-916)
(  0) 0) |
| [4] |
范长新. 全球海潮模型最新进展及在中国沿海精度评估[J]. 大地测量与地球动力学, 2019, 39(5): 476-481 (Fan Changxin. Latest Advances of Global Ocean Tide Models and Their Accuracy Comparisons in Coastal Areas of China[J]. Journal of Geodesy and Geodynamics, 2019, 39(5): 476-481)
(  0) 0) |
| [5] |
王继刚, 周江存. 沿海和岛屿重力海潮负荷改正模型——以马祖岛为例[J]. 大地测量与地球动力学, 2020, 40(8): 794-798 (Wang Jigang, Zhou Jiangcun. Correction Model of Ocean Tide Loading on Gravity over Coastal Area and Islands: A Case Study of Matzu Island[J]. Journal of Geodesy and Geodynamics, 2020, 40(8): 794-798)
(  0) 0) |
| [6] |
赵珞成, 罗志才, 许闯, 等. 岛礁重力测量潮汐改正新方法[J]. 武汉大学学报: 信息科学版, 2015, 40(7): 913-917 (Zhao Luocheng, Luo Zhicai, Xu Chuang, et al. The New Method of Tidal Correction for Gravity Measurement on Island[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 913-917)
(  0) 0) |
| [7] |
王振宇, 王赟, 徐如刚, 等. 淮南深地重力观测的环境噪声评估与慢地震探测潜力[J]. 地球物理学报, 2022, 65(12): 4555-4568 (Wang Zhenyu, Wang Yun, Xu Rugang, et al. Environmental Noise Assessment of Underground Gravity Observation in Huainan and the Potential Capability of Detecting Slow Earthquake[J]. Chinese Journal of Geophysics, 2022, 65(12): 4555-4568)
(  0) 0) |
| [8] |
Camp M, Vauterin P. Tsoft: Graphical and Interactive Software for the Analysis of Time Series and Earth Tides[J]. Computers and Geosciences, 2005, 31(5): 631-640
(  0) 0) |
| [9] |
杨锦玲, 关玉梅, 钟继茂, 等. 厦门重力固体潮海潮负荷改正研究[J]. 地球物理学进展, 2016, 31(3): 992-998 (Yang Jinling, Guan Yumei, Zhong Jimao, et al. Study on Ocean Tidal Loading Correction of Tidal Gravity at Xiamen Station[J]. Progress in Geophysics, 2016, 31(3): 992-998)
(  0) 0) |
| [10] |
周东旭, 孙维康, 付海德, 等. 三种最新全球海潮模型在中国沿海的精度评估[J]. 海洋科学进展, 2023, 41(1): 54-63 (Zhou Dongxu, Sun Weikang, Fu Haide, et al. Accuracy Assessment of Three Latest Global Ocean Tide Models in Coastal Areas of China[J]. Advances in Marine Science, 2023, 41(1): 54-63)
(  0) 0) |
| [11] |
Agnew D C. NLOADF: A Program for Computing Ocean-Tide Loading[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5109-5110
(  0) 0) |
| [12] |
杨锦玲, 杨小林, 李军, 等. 东南沿海区域重力微震信号特征分析[J]. 地球物理学进展, 2021, 36(6): 2362-2370 (Yang Jinling, Yang Xiaolin, Li Jun, et al. Characteristics of Microseisms in Southeast Coastal China Based on Gravity Observations[J]. Progress in Geophysics, 2021, 36(6): 2362-2370)
(  0) 0) |
| [13] |
Carrere L, Lyard F, Cancet M, et al. FES2014, a New Tidal Model: Validation Results and Perspectives for Improvements[R]. ESA Living Planet Conference, Paris, 2016
(  0) 0) |
| [14] |
Lyard F H, Allain D J, Cancet M, et al. FES2014 Global Ocean Tide Atlas: Design and Performance[J]. Ocean Science, 2021, 17(3): 615-649
(  0) 0) |
2. Fujian Seismic Station, 7 Huahong Road, Fuzhou 350003, China;
3. The First Monitoring and Application Center, CEA, 7 Naihuo Road, Tianjin 300180, China
 2023, Vol. 43
2023, Vol. 43


