2. 中国科学院精密测量科学与技术创新研究院,武汉市徐东大街340号,430077;
3. 云南省地震局丽江地震监测中心站,云南省丽江市教育路462号,674100;
4. 兰州交通大学测绘与地理信息学院,兰州市安宁西路88号,730070;
5. 中国地质大学(北京)地球物理与信息技术学院,北京市学院路29号,100083
超导重力仪是目前性能最好的相对重力观测仪器,具有精度高、稳定性好、漂移率低等特点。从其观测数据中提取有效的震前重力变化异常和同震重力变化信息有助于地震预测和震源机制的研究。Imanishi等[1]从超导重力观测数据的重力残差中成功检测到2003年日本十胜近海地震小于10 nm/s2的同震重力变化,该观测值与地震位错理论的模拟结果相吻合。在超导重力数据的解释过程中,地震位错理论[2-5]发挥着重要的支撑作用,但并非所有地震引起的重力变化观测结果都可以用该理论进行较好地解释。如Xing等[6]对2015年尼泊尔MW7.9地震进行研究,发现丽江台和武汉台的同震重力变化观测值超过相应的理论值1个量级。上述研究中,同震重力变化观测结果的可靠性鲜有提及或者进行深入研究。
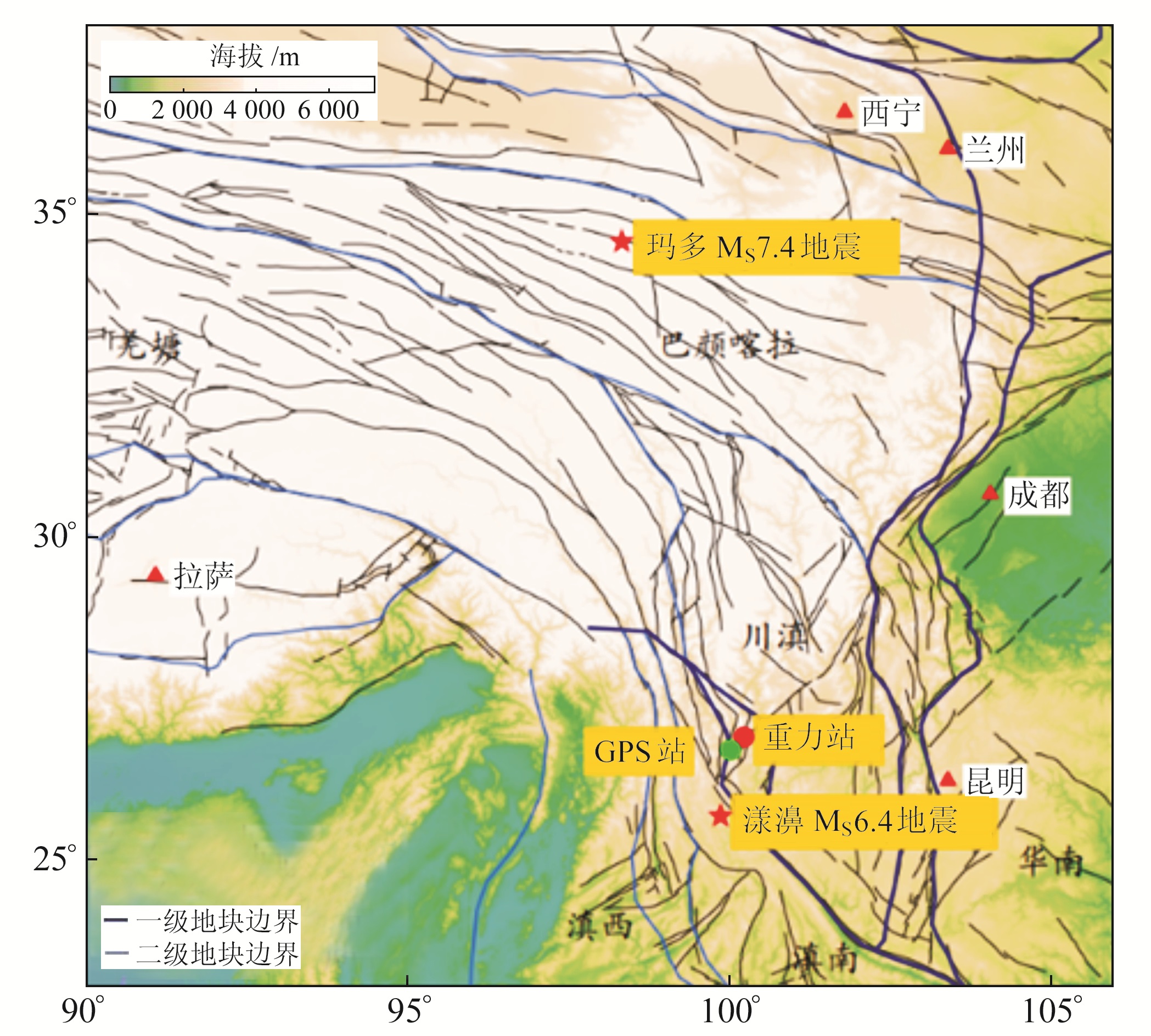
UTC 2021-05-21 13:48:34云南漾濞发生MS6.4地震,同日UTC 18:04:11青海玛多发生MS7.4地震,2次地震间隔很短,均位于青藏地块东部。丽江台距漾濞地震震中140.53 km,距玛多地震震中872.02 km(图 1)。台站现有1台GWR型超导重力仪(OSG-066),从2013-07开始正常工作,记录了近场漾濞地震和远场玛多地震发生期间的重力变化时间序列,为地震重力变化观测值与理论值的拟合度及其解释工作提供了研究资料。在提取同震重力变化的研究过程中,迄今为止的研究对象多为单次地震,而漾濞地震与玛多地震是短时间内连续发生的2次大地震,可利用2次地震之间的记录数据充分讨论仪器的记录能力,研究超导重力同震观测数据的可靠性。鉴于此,本文基于丽江台的超导重力仪记录的连续重力观测数据,结合地下水和GPS高频数据,利用球体地球地震位错理论和三维不均匀地球潮汐理论开展研究,以解释漾濞地震与玛多地震在丽江台引起的同震重力变化。
|
图 1 漾濞MS6.4、玛多MS7.4地震和丽江台位置 Fig. 1 Location of Yangbi MS6.4, Maduo MS7.4 earthquakes and Lijiang station |
从观测数据中尽可能地扣除潮汐、大气、极移和周日长、地球横向不均匀性、地下水位变化等的影响,得到重力残差时间序列,然后拟合地震时刻残差值的变化量,通过对比得到同震重力变化[7]。选取丽江台超导重力仪2021-05-21 00:00:00~2021-05-22 12:00:00的秒采样观测数据作为提取此次同震重力变化的基础数据,包括重力和台站气压数据,重力数据的格值为-96.331 9 μGal/V,气压数据的格值为1 000 hPa/V。在计算重力残差、提取同震重力变化之前,首先对观测数据作倾斜改正,相关X、Y方向水平因子见图 2。

|
图 2 超导重力仪附加倾斜数据 Fig. 2 Additional leveling data of superconducting gravimeter |
利用Tsoft软件对原始观测数据进行预处理[8-9],得到预处理之后的数据gob,见图 3(a),图中红、蓝线分别为漾濞和玛多地震发生时间,其中,漾濞MS6.4地震发生前观测数据的较大波动是前震所致。潮汐改正过程中,由于地球固体潮与相应的海潮成分的频率几乎一致,通常采用计算合成潮的方法将固体潮与海潮的影响同时剔除作为潮汐改正。本文利用Eterna软件[10-11],结合台站2020-01-01~2021-06-30的观测数据,利用调和分析方法构建当地重力合成潮,并用于潮汐改正,结果见图 3(c)。

|
图 3 超导重力观测数据的调和分析结果 Fig. 3 Harmonic analysis results of superconducting gravity observation data |
气压数据见图 3(d)。去除重力观测中气压变化引起的重力效应的基本思路是利用与重力观测同址、同期的气压观测数据,通过大气导纳得到气压重力响应值。大气压力引起的重力变化为:
| $ g_{\text {air }}=\mathrm{ap} \cdot \operatorname{adm}_{\mathrm{ap}} $ | (1) |
式中,gair为气压引起的重力变化,ap为气压值(单位为hPa),admap为气压的导纳系数。将气压观测数据代入到Eterna的潮汐分析中,求出大气导纳值为-3.204 9 nm/(s2·hPa),再通过式(1)得到气压重力响应值。漾濞和玛多地震发生前后1 d时间内,丽江台附近大气压力变化达到3 hPa左右,相应的重力变化接近10 nm/s2。
极移产生的重力效应gPT与周日长变化的影响gLOD可通过国际地球自转和参考系统服务提供的地球定向参数计算得到,其重力效应分别见图 3(e)和3(f)。
用EMC-GyPSuM模型(http://ds.iris.edu/ds/products/emc-gypsum/)计算地球横向不均匀性所导致的潮汐改正偏差对重力的影响,见图 3(g)。
丽江地区地表的水文变化非常剧烈,地下水位变化对重力影响显著。丽江台地下水位变化数据见图 3(h)。超导重力仪周围的水循环导致的重力变化与地表形变和气压重力效应相似,二者的相关性可以通过计算地下水位重力导纳系数确定。用布格平板模型计算地下水的重力效应:
| $ g_{\mathrm{gwl}}=2 {\rm{ \mathsf{ π} }} G \rho_{\mathrm{w}} h_{\mathrm{gwl}} P_{\mathrm{s}}=C_{\mathrm{gwl}} h_{\mathrm{gwl}} $ | (2) |
式中,G为引力常数,ρw为水的密度,Ps为土壤孔隙度,取0.02[12],hgwl为地下水位高度值,Cgwl为地下水位数据和重力的相关系数。由布格平板模型计算得到Cgwl=8.381 2 nm/(s2·m)。
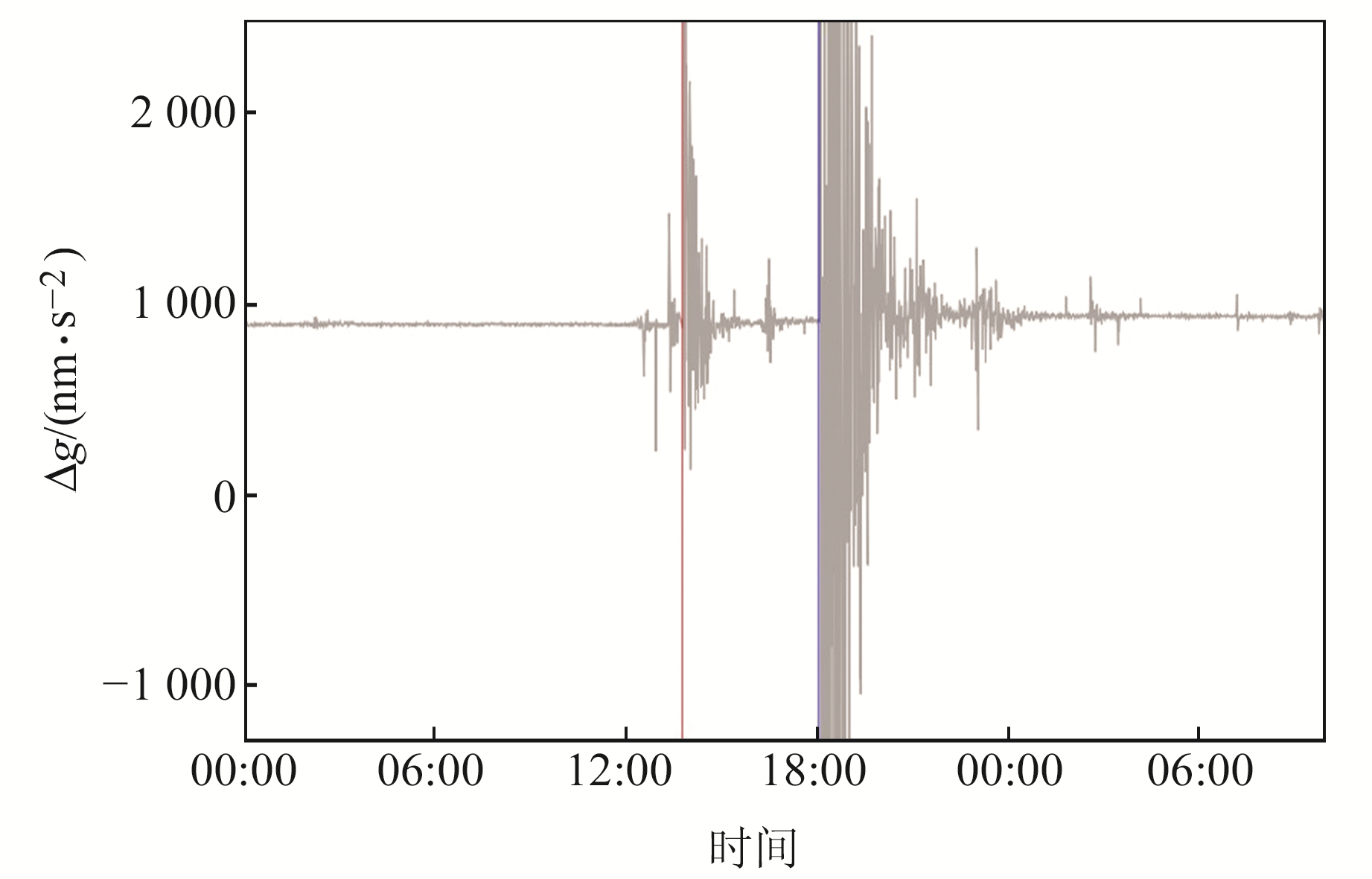
2 同震观测与模拟结果 2.1 超导重力仪同震重力变化观测值根据上节方法,利用式(3)对丽江台超导重力仪的观测数据进行处理,并进一步计算漾濞和玛多地震产生的同震重力变化,评估超导重力仪在地震发生前后的稳定性。得到的重力残差序列Δg见图 4:
| $ \begin{gathered} \Delta g=g_{\mathrm{ob}}-t_i-l_i-g_{\mathrm{air}}-g_{\mathrm{PT}}- \\ g_{\mathrm{LOD}}-g_{\mathrm{LI}}-g_{\mathrm{gwl}} \end{gathered} $ | (3) |
|
图 4 漾濞和玛多地震前后丽江台重力残差时间序列 Fig. 4 Time series of gravity residuals before and after Yangbi and Maduo earthquakes at Lijiang station |
地震发生时,断层破裂产生地震波,并引起瞬时质量重分布与密度变化[13]。由图 4可知,丽江台超导重力仪记录到漾濞和玛多地震产生的剧烈振荡的地震波信号[14],使得主震发生后一定时间内重力残差数据变化幅度较大。为了更准确地拟合出重力残差的变化趋势,扣除震后短时间内振荡剧烈的残差数据;同时,为了减小结果的偏差,尽可能缩短被剔除数据的时间跨度。
在提取同震重力变化时,将2次地震前后的数据分别利用二次函数进行拟合。根据地震发生的时间,将地震前后的重力残差时间序列(图 4)分为3个部分:2021-05-21 00:00:00~13:48:00、2021-05-21 14:40:00~18:04:00、2021-05-21 22:00:00~2021-05-22 10:00:00。利用式(4)分别拟合3个部分数据[2]。
| $ g(t)=a+b t+c t^2 $ | (4) |
然后分别计算3段数据拟合得出的二次函数在漾濞地震发生时刻(t0)与玛多地震发生时刻(t1)的数值并作差,计算同震重力变化。
漾濞地震的同震重力变化观测结果为:
| $ \Delta g(\mathrm{YB})=g_2\left(t_0\right)-g_1\left(t_0\right) $ | (5) |
玛多地震的同震重力变化观测结果为:
| $ \Delta g(\mathrm{MD})=g_3\left(t_1\right)-g_2\left(t_1\right) $ | (6) |
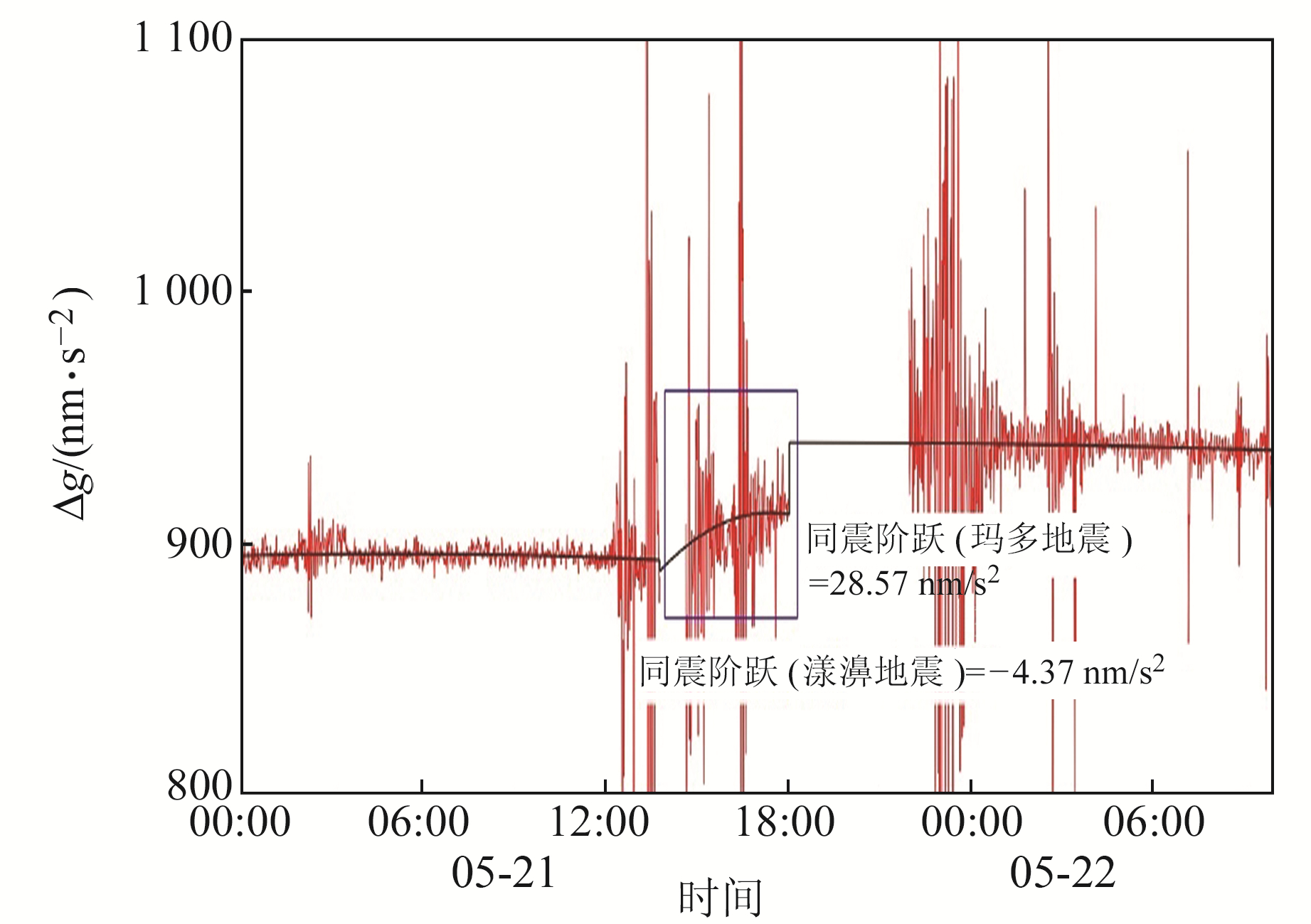
计算得出g1(t0)、g2(t0)、g2(t1)、g3(t1)的值,见表 1,同震重力变化观测结果见图 5。
|
|
表 1 漾濞和玛多地震前后丽江台超导重力数据拟合值 Tab. 1 Fitting values of superconducting gravity data before and after Yangbi and Maduo earthquakes at Lijiang station |
|
图 5 超导重力仪检测到的同震重力变化信号 Fig. 5 The coseismic gravity changes detected by the superconducting gravimeter |
由表 1和图 5可以看出,漾濞地震同震阶跃为-4.37 nm/s2,玛多地震同震阶跃为28.57 nm/s2。此外,在漾濞地震之后、玛多地震之前,超导重力仪观测到显著的重力变化,该变化是漾濞地震的余滑信号、玛多地震的前兆信号,还是仪器失稳所致,需进一步研究。
2.2 基于地震位错理论的重力变化理论值地震位错理论被广泛地应用于地震断层破裂反演、地震变形数据和大地测量数据解释工作中,为研究同震和震后重力变化等提供了有力的理论工具。利用Sun等[4-5]基于球体分层结构的球形地球位错理论,计算漾濞和玛多地震在丽江台产生的同震重力变化[15],其中玛多地震的断层滑动模型参考Hong等[16]和张克亮等[17]的断层几何模型。理论值与观测值的对比结果见表 2,可以看出,观测值总体上比理论值大1~2个数量级。这一差异很难用计算方法、反演精度、地形效应、余震效应等导致的计算误差进行解释。
|
|
表 2 漾濞和玛多地震在丽江台引起的同震重力变化观测值与理论值 Tab. 2 Observed and theoretical coseismic gravity changes caused by Yangbi and Maduo earthquakes at Lijiang station |
本节拟从超导重力仪观测值与理论值的异同、环境因素的重力变化效应改正、同址GPS观测数据反映的垂直位移与仪器的短期失稳现象3个方面讨论丽江台超导重力仪观测数据与地震位错理论模拟值相差较大的原因,以揭示本次重力变化观测信号的形成机理。
3.1 超导重力仪观测值与理论值的异同观测精度较高的超导重力仪检测的同震重力变化信号不但可以为检验和完善位错模型提供参考资料,而且可以用来讨论重力观测仪器在地震发生时的稳定性。
Xing等[6]研究2015年尼泊尔MW7.8地震的同震重力变化,认为地震发生时瞬时重力变化不仅与地震本身相关,还与重力台站背景构造应力特征和当时观测环境瞬时变化情况相关。韦进等[18]研究玛多MS7.4地震800 km范围内5个远场gPhone连续重力观测台站的观测数据,结合中甸台观测数据,讨论了漾濞MS6.4地震对玛多MS7.4地震同震重力变化估算结果的影响,发现经过漾濞MS6.4地震影响改正后,玛多MS7.4地震的观测值更接近于理论值。说明存在受到先发生地震的影响导致仪器不稳定,使后发生地震的观测值过大的情况。
由此可见,对于连续发生的2次地震,仪器的稳定性会受先发生地震的影响,导致后一个地震的观测值与理论值差异更显著。鉴于此,本文在考虑区域性地下水位变化的重力改正效果的基础上,进一步讨论地震发生时仪器的不稳定现象。
3.2 环境因素的重力变化效应计算与改正由于超导重力仪较高的敏感度,观测数据会不可避免地受到多种因素的影响,在提取同震重力变化信号时,合理剔除环境因素的影响尤为重要。潮汐、气压、极移和周日长产生的重力效应已经可以采用成熟的平台或模型精确地计算出来,而局部区域地下水效应则需根据实测地下水数据进行计算。
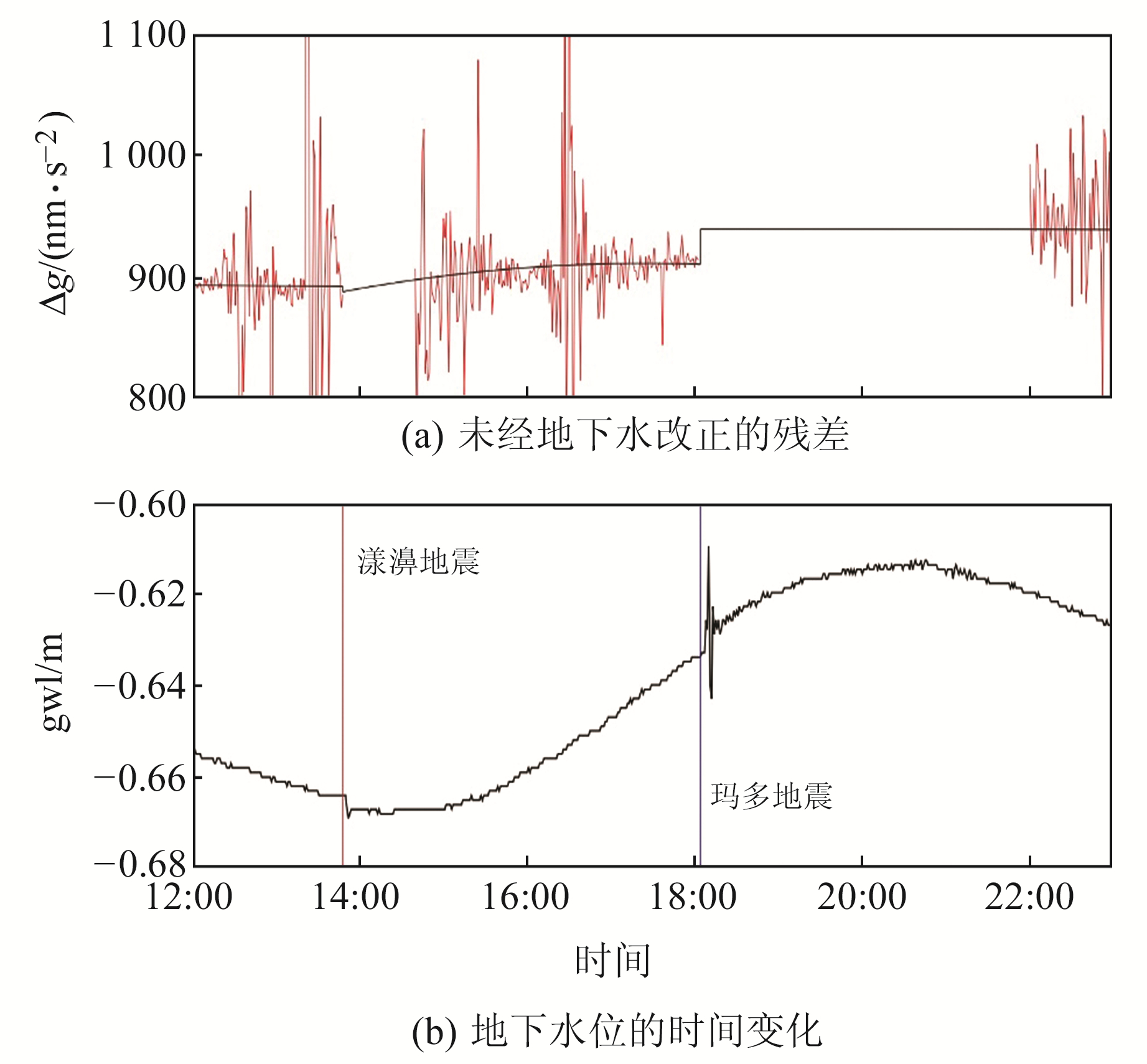
局部地下水引起的重力变化可达10 μGal以上。图 6(a)为未经地下水改正的重力残差,图 6(b)为水井的水位观测记录,0起始面选在丽江一泄洪口高程2 405 m的位置,采样间隔为1 min。从图 6可以看出,地震发生时,地下水位记录数据出现明显的波动。漾濞地震地下水位的同震阶跃为-0.005 m,玛多地震的同震阶跃为0.007 m。将地下水数据与未经地下水改正的重力残差对比,发现二者在地震发生时变化趋势一致,表明重力残差中的一部分信号来源于局部区域地下水变化产生的重力效应。
|
图 6 漾濞和玛多地震前后丽江台的重力残差与地下水位变化 Fig. 6 Gravity residuals and groundwater level changes before and after Yangbi and Maduo earthquakes at Lijiang station |
布格平板模型的计算结果表明,丽江台周边区域地下水变化在漾濞和玛多地震发生时分别引起-0.04 nm/s2和0.06 nm/s2的重力变化,和同震重力变化理论值(-0.19 nm/s2、0.24 nm/s2)相近,详细结果见表 3。因此,计算同震重力变化时,须考虑到观测站附近地下水的影响。
|
|
表 3 丽江台同震重力变化理论值与地下水重力效应的对比 Tab. 3 Comparison of theoretical coseismic gravity variation and groundwater effect on gravity at Lijiang station |
然而,从重力观测数据中扣除众多已知的影响因素之后,发现观测值和理论值虽然符号相同,但大小仍然存在差异。Imanishi等[1]利用江刺、松本、京都3个台站超导重力数据提取2003年日本十胜近海MW8.0地震的同震重力变化,观测值分别为0.58 μGal、0.10 μGal、0.07 μGal,而利用球形地球位错理论计算的理论重力变化则为0.575±0.007 μGal、0.096±0.005 μGal、0.070±0.009 μGal,与观测值十分接近,说明球形地震位错理论的计算结果是基本可信的。本文观测值与理论值振幅相差较大,难以用理论计算的精度进行解释,故实测重力变化值除受到上述已扣除的影响之外,应该还受到其他重要因素的影响。
3.3 超导重力仪的短期失稳现象从图 5中可以看出,相比于漾濞地震在丽江台引起的同震重力变化观测值(-4.37 nm/s2),后续发生的玛多地震引起的重力变化观测值(28.57 nm/s2)与理论值的差距更大。玛多地震后由于地震激发的振荡,被剔除数据的时间跨度也比漾濞地震更长(图 5中时间序列的空白部分)。引起这种现象的可能原因为:超导重力仪在观测重力变化的过程中,受到漾濞地震前震的影响(脉冲效应),出现仪器短期失稳现象,导致漾濞地震的观测值与理论值不符(图 5中蓝色方框)。之后玛多地震发生时,仪器还没有恢复稳定,再次受到地震的脉冲效应,导致仪器在震后出现更长时间跨度的振荡,同时使得玛多地震的观测值比漾濞地震大5倍以上。而玛多地震后并未出现失稳的现象,可能是因为对于丽江台来说,漾濞地震为近场地震,玛多地震为远场地震,超导重力仪对于远场和近场地震的响应有所不同。
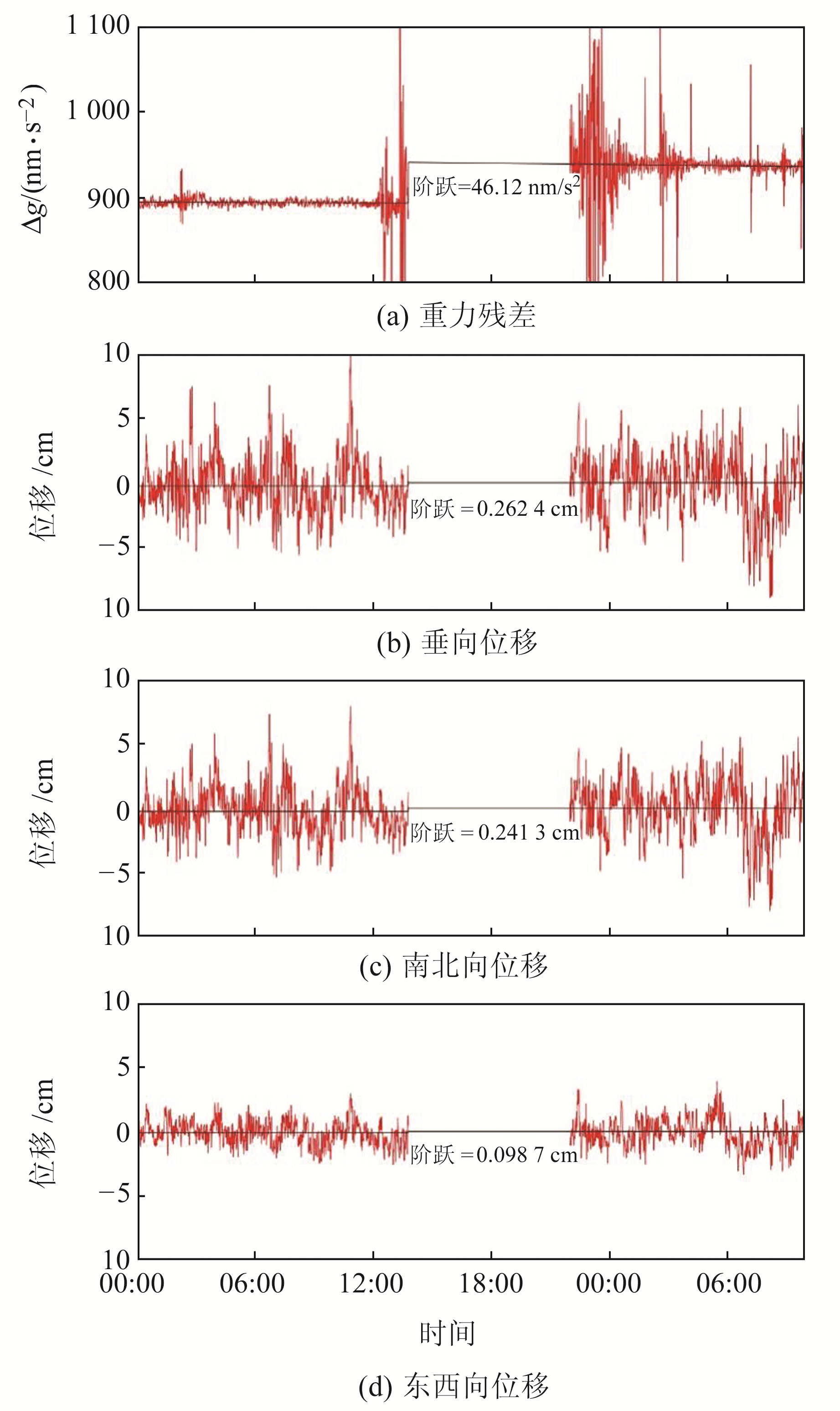
为确认此现象出现的原因,收集并处理丽江连续观测站30 s采样的高频GPS数据,通过拟合获取漾濞和玛多地震前后的位移场时间序列,然后对比GPS位移数据与重力残差数据的变化趋势,结果见图 7,图 7(a)~7(d)分别表示重力残差和3个方向的位移结果。可以看出,2次地震共同引起的重力残差的阶跃值为46.12 nm/s2,在同一时间段GPS站观测到的垂向位移约为0.26 cm,南北向的位移约为0.24 cm,东西向的位移约为0.10 cm。
|
图 7 2次地震前后丽江地区超导重力仪与GPS观测的同震变化结果 Fig. 7 Coseismic gravity changes detected by superconducting gravimeter and GPS before and after two earthquakes in Lijiang area |
同震重力变化一般受观测站的垂向变动以及地球内部物质的再分布的影响[19],且前者在多数情况下占主导地位。因此,本文将考虑0.26 cm的垂向位移伴随的重力变化量(地壳水平位移对重力场的贡献很小,可忽略不计)。重力变化和垂向位移的关系如式(7):
| $ \frac{\partial g}{\partial d}=-30.86 \mathrm{~nm} /\left(\mathrm{s}^2 \cdot \mathrm{cm}\right) $ | (7) |
式中,g为重力值,d为测点与地心的距离[20]。2个地震在丽江地区引起的垂向位移约为0.26 cm,其对应的重力变化约为8.02 nm/s2,远小于超导重力仪观测的46.12 nm/s2。即GPS数据在地震前后没有明显的差异。鉴于此,本文认为图 5蓝色方框中重力残差信号的显著变化是因为地震脉冲使重力仪失稳,导致2次地震的同震重力观测数据均明显大于理论值。Xing等[6]的研究也表明,重力仪器受到地震的脉冲信号影响而产生的失稳并非个别现象。因此,利用超导重力仪提取地震同震重力变化时,有必要考虑重力仪对地震信号的脉冲响应。
4 结语1) 通过对超导重力数据的处理,提取到漾濞MS6.4和玛多MS7.4地震的同震重力变化值分别为-4.37 nm/s2和28.57 nm/s2,较地震位错理论的计算值大1~2个量级;
2) 丽江台周边地区地下水变化产生的重力效应与地震产生的重力变化理论值处于同一量级;
3) 结合GPS、地下水等观测资料,分析同震重力变化理论值与超导重力仪观测值差异的可能原因,认为丽江台的超导重力仪在相继发生的漾濞MS6.4和玛多MS7.4地震期间受地震脉冲的影响,在短时间内产生明显的失稳现象(重力变化幅度增大)。
| [1] |
Imanishi Y, Sato T, Higashi T, et al. A Network of Superconducting Gravimeters Detects Submicrogal Coseismic Gravity Changes[J]. Science, 2004, 306(5 695): 476-478
(  0) 0) |
| [2] |
Sun W K, Okubo S. Surface Potential and Gravity Changes Due to Internal Dislocations in a Spherical Earth-Ⅰ. Theory for a Point Dislocation[J]. Geophysical Journal International, 1993, 114(3): 569-592 DOI:10.1111/j.1365-246X.1993.tb06988.x
(  0) 0) |
| [3] |
Sun W K, Okubo S. Surface Potential and Gravity Changes Due to Internal Dislocations in a Spherical Earth-Ⅱ. Application to a Finite Fault[J]. Geophysical Journal International, 1998, 132(1): 79-88
(  0) 0) |
| [4] |
Sun W K, Okubo S, Fu G Y. Green's Functions of Coseismic Strain Changes and Investigation of Effects of Earth's Spherical Curvature and Radial Heterogeneity[J]. Geophysical Journal International, 2006, 167(3): 1273-1291 DOI:10.1111/j.1365-246X.2006.03089.x
(  0) 0) |
| [5] |
Sun W K, Okubo S, Fu G Y, et al. General Formulations of Global Co-Seismic Deformations Caused by an Arbitrary Dislocation in a Spherically Symmetric Earth Model-Applicable to Deformed Earth Surface and Space-Fixed Point[J]. Geophysical Journal International, 2009, 177(3): 817-833 DOI:10.1111/j.1365-246X.2009.04113.x
(  0) 0) |
| [6] |
Xing L L, Liu Z W, Jia J G, et al. Far-Field Coseismic Gravity Changes Related to the 2015 MW7.8 Nepal(Gorkha) Earthquake Observed by Superconducting Gravimeters in Chinese Mainland[J]. Earth and Planetary Physics, 2021, 5(2): 141-148 DOI:10.26464/epp2021018
(  0) 0) |
| [7] |
徐建桥, 许厚泽, 孙和平, 等. 武汉台重力长期变化分析[J]. 地壳形变与地震, 1998, 18(3): 67-72 (Xu Jianqiao, Xu Houze, Sun Heping, et al. Analysis of the Long-Term Gravity Variations at Wuhan Station[J]. Crustal Deformation and Earthquake, 1998, 18(3): 67-72)
(  0) 0) |
| [8] |
Camp M, Vauterin P. Tsoft: Graphical and Interactive Software for the Analysis of Time Series and Earth Tides[J]. Computers and Geosciences, 2005, 31(5): 631-640 DOI:10.1016/j.cageo.2004.11.015
(  0) 0) |
| [9] |
陈晓东, 孙和平. 一种新的重力潮汐数据预处理和分析方法[J]. 大地测量与地球动力学, 2002, 22(3): 83-87 (Chen Xiaodong, Sun Heping. New Method for Pre-Processing and Analyzing Tidal Gravity Observations[J]. Journal of Geodesy and Geodynamics, 2002, 22(3): 83-87)
(  0) 0) |
| [10] |
Wenzel H G. Earth Tide Analysis Package ETERNA 3.0[J]. Bulletin d'Informations de Marees Terrestres, 1994, 118: 8719-9722
(  0) 0) |
| [11] |
Wenzel H G. The Nanogal Software: Earth Tide Data Processing Package ETERNA 3.30[J]. Bulletin d'Information de Marees Terrestres, 1996, 124: 9425-9439
(  0) 0) |
| [12] |
Xing L L, Niu X W, Bai L, et al. Monitoring Groundwater Storage Changes in a Karst Aquifer Using Superconducting Gravimeter OSG-066 at the Lijiang Station in China[J]. Pure and Applied Geophysics, 2022, 179(5): 1853-1870 DOI:10.1007/s00024-022-03024-w
(  0) 0) |
| [13] |
Zhang S J, Wang R J, Dahm T, et al. Prompt Elasto-Gravity Signals(PEGS) and Their Potential Use in Modern Seismology[J]. Earth and Planetary Science Letters, 2020, 536
(  0) 0) |
| [14] |
Kame N, Kimura M. The Fundamental Nature of a Transient Elastic Response to Prompt Gravity Perturbations[J]. Geophysical Journal International, 2019, 218(2): 1136-1142 DOI:10.1093/gji/ggz196
(  0) 0) |
| [15] |
付广裕, 刘泰. 基于粘弹性球体地球模型的震后位移与重力变化计算软件[J]. 大地测量与地球动力学, 2017, 37(7): 661-667 (Fu Guangyu, Liu Tai. A User-Friendly Code for Calculating Post-Seismic Displacements and Gravity Changes on a Symmetric Viscoelastic Spherical Earth[J]. Journal of Geodesy and Geodynamics, 2017, 37(7): 661-667)
(  0) 0) |
| [16] |
Hong S Y, Liu M, Liu T, et al. Fault Source Model and Stress Changes of the 2021 MW7.4 Maduo Earthquake, China, Constrained by InSAR and GPS Measurements[J]. Bulletin of the Seismological Society of America, 2022, 112(3): 1284-1296
(  0) 0) |
| [17] |
张克亮, 甘卫军, 梁诗明, 等. 2021年5月21日MS6.4漾濞地震GNSS同震变形场及其约束反演的破裂滑动分布[J]. 地球物理学报, 2021, 64(7): 2253-2266 (Zhang Keliang, Gan Weijun, Liang Shiming, et al. Coseismic Displacement and Slip Distribution of the 2021 May 21, MS6.4, Yangbi Earthquake Derived from GNSS Observations[J]. Chinese Journal of Geophysics, 2021, 64(7): 2253-2266)
(  0) 0) |
| [18] |
韦进, 郝洪涛, 韩宇飞, 等. 基于连续重力台观测的玛多MS7.4地震的同震重力变化特征[J]. 地震地质, 2021, 43(4): 984-998 (Wei Jin, Hao Hongtao, Han Yufei, et al. Study on the Characteristics of Co-Seismic Gravity Change Induced by Maduo MS7.4 Earthquake Based on Observations of Continuous Gravity Stations[J]. Seismology and Geology, 2021, 43(4): 984-998)
(  0) 0) |
| [19] |
Okubo S. Potential and Gravity Changes Raised by Point Dislocations[J]. Geophysical Journal International, 1991, 105(3): 573-586
(  0) 0) |
| [20] |
曾融生. 固体地球物理学导论[M]. 北京: 科学出版社, 1984 (Zeng Rongsheng. Introduction to Solid Geophysics[M]. Beijing: Science Press, 1984)
(  0) 0) |
2. Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China;
3. Lijiang Earthquake Monitoring Center Station of Yunnan Earthquake Agency, 462 Jiaoyu Road, Lijiang 674100, China;
4. Faculty of Geomatics, Lanzhou Jiaotong University, 88 West-Anning Road, Lanzhou 730070, China;
5. School of Geophysics and Information Technology, China University of Geosciences, 29 Xueyuan Road, Beijing 100083, China
 2023, Vol. 43
2023, Vol. 43


