2. 广东工业大学土木与交通工程学院,广州市外环西路100号,510006
GRACE和GRACE-FO卫星为解算高精度的月时变地球重力场模型提供了重要的数据支撑,具备监测地表质量变化与迁移的能力[1-2]。但GRACE与GRACE-FO卫星间存在衔接空白。欧洲航天局2013-11发射的3颗搭载磁测仪器、GPS接收机等设备的SWARM卫星为监测全球质量变化提供了可替换的手段[3]。AIUB(Astronomical Institute University Bern)、ASU(Astronomical Institute Ond Arˇ ejov)、OSU(Ohio State University)和IGG(Institute of Geodesy and Geophysics) 等科研机构分别采用天体力学、加速度、改进能量以及短弧积分等方法开展SWARM卫星月时变重力场模型的反演研究。短弧积分法是将弧段积分方程中任意历元的卫星状态向量表示为边界轨道参数、待估重力场参数和其他加速度参数的函数,由于引入边值条件,有利于抑制轨道积分误差的累积,引入几何轨道梯度改正后可减小观测误差对系数矩阵的影响。该方法法方程条件数较小,解算结果稳定,精度较高,已成功用于CHAMP和SWARM等低轨卫星重力反演[4-7]。有研究表明,SWARM卫星数据可有效填补GRACE/GRACE-FO在亚马孙流域的数据空白[8]。
鉴于SWARM时变重力场具有重要的科学意义和应用价值,以及短弧积分法的优势,本文采用短弧积分法解算2015~2021年共84个月的SWARM月时变重力场模型,并与ASU、COST-G、IGG等机构发布的SWARM月时变重力场模型以及ITSG发布的GRACE/GRACE-FO月时变重力场模型进行对比,以探究SWARM月时变重力场模型的精度及其用于监测区域陆地水储量变化的可行性。
1 短弧积分法反演重力场基本原理短弧积分法是基于牛顿运动方程导出的,假设卫星在某一弧段边界点的位置向量分别为rA和rB,积分弧段长度为T,则任意τ时刻卫星位置r(τ)与rA、rB及卫星受力间的关系为[9]:
| $ \begin{gathered} \boldsymbol{r}(\tau)=\boldsymbol{r}_A(1-\tau)+\boldsymbol{r}_B(\tau)- \\ T^2 \int_0^1 K\left(\tau, \tau^{\prime}\right) a\left(\boldsymbol{r}\left(\tau^{\prime}\right), u, p\right) \mathrm{d} \tau^{\prime} \end{gathered} $ | (1) |
式中,rA=r(tA),rB=r(tB),τ=
| $ K\left(\tau, \tau^{\prime}\right)=\left\{\begin{array}{l} \tau^{\prime}(1-\tau), \tau^{\prime} \leqslant \tau \\ \tau\left(1-\tau^{\prime}\right), \tau^{\prime}>\tau \end{array}\right. $ | (2) |
若卫星轨道观测向量为robs(τ),轨道改正量为Δrobs(τ),以轨道观测向量为初值,将式(1)右端最后一项线性化为:
| $ \begin{gathered} T^2 \int_0^1 K\left(\tau, \tau^{\prime}\right) a\left(\boldsymbol{r}\left(\tau^{\prime}\right), u, p\right) \mathrm{d} \tau^{\prime}= \\ T^2 \int_0^1 K\left(\tau, \tau^{\prime}\right) a\left(\boldsymbol{r}_{\text {obs }}\left(\tau^{\prime}\right), u, p\right) \mathrm{d} \tau^{\prime}+ \\ T^2 \int_0^1 K\left(\tau, \tau^{\prime}\right) \frac{\partial a\left(\boldsymbol{r}_{\text {obs }}\left(\tau^{\prime}\right), u, p\right)}{\partial \boldsymbol{r}_{\text {obs }}\left(\tau^{\prime}\right)} \Delta \boldsymbol{r}_{\text {obs }}\left(\tau^{\prime}\right) \mathrm{d} \tau^{\prime} \end{gathered} $ | (3) |
采用短弧积分法反演重力场时,首先利用式(1)和(3)给定初始重力场参数u0、先验加速度参数p0以及其他力模型,基于轨道观测数据robs、先验边界轨道参数rA0和rB0,利用最小二乘方法解算轨道改正量Δrobs;然后计算参考轨道向量rref(τ)=robs(τ)+Δrobs(τ);最后在参考轨道向量rref(τ)处对卫星轨道位置观测方程进行线性化:
| $ \boldsymbol{r}(\tau)=\boldsymbol{r}_{\mathrm{ref}}(\tau)+\left.\frac{\partial \boldsymbol{r}(\tau)}{\partial \boldsymbol{\beta}}\right|_{\boldsymbol{\beta}=\boldsymbol{\beta}_0} \delta \boldsymbol{\beta} $ | (4) |
式(4)即为利用短弧积分法反演重力场的基本观测方程,其中,β为待估边界轨道参数、重力场参数和加速度参数向量,β0为其先验值。其他参数和详细计算过程可参考文献[9]。
2 TVG-SWARM月时变重力场解算与精度分析 2.1 TVG-SWARM月时变重力场解算基于短弧积分法,采用45 min弧长,利用SWARM的3颗低轨卫星解算2015-01~2021-12共84个月的月尺度时变重力场模型,命名为TVG-SWARM(time-variable gravity SWARM)。考虑到利用SWARM轨道数据反演月时变重力场模型时,随着阶次增加,阶误差迅速增大,因此SWARM月时变重力场模型的最高阶次只选为40,这也与国际其他机构的SWARM月时变重力场模型空间分辨率一致。所使用的数据为SWARM卫星的简化动力学轨道、几何轨道以及ITSG提供的非保守力模型等,均为ITSG的产品,解算所采用的摄动力模型和有关信息见表 1。
|
|
表 1 摄动力模型信息 Tab. 1 Perturbation model information |
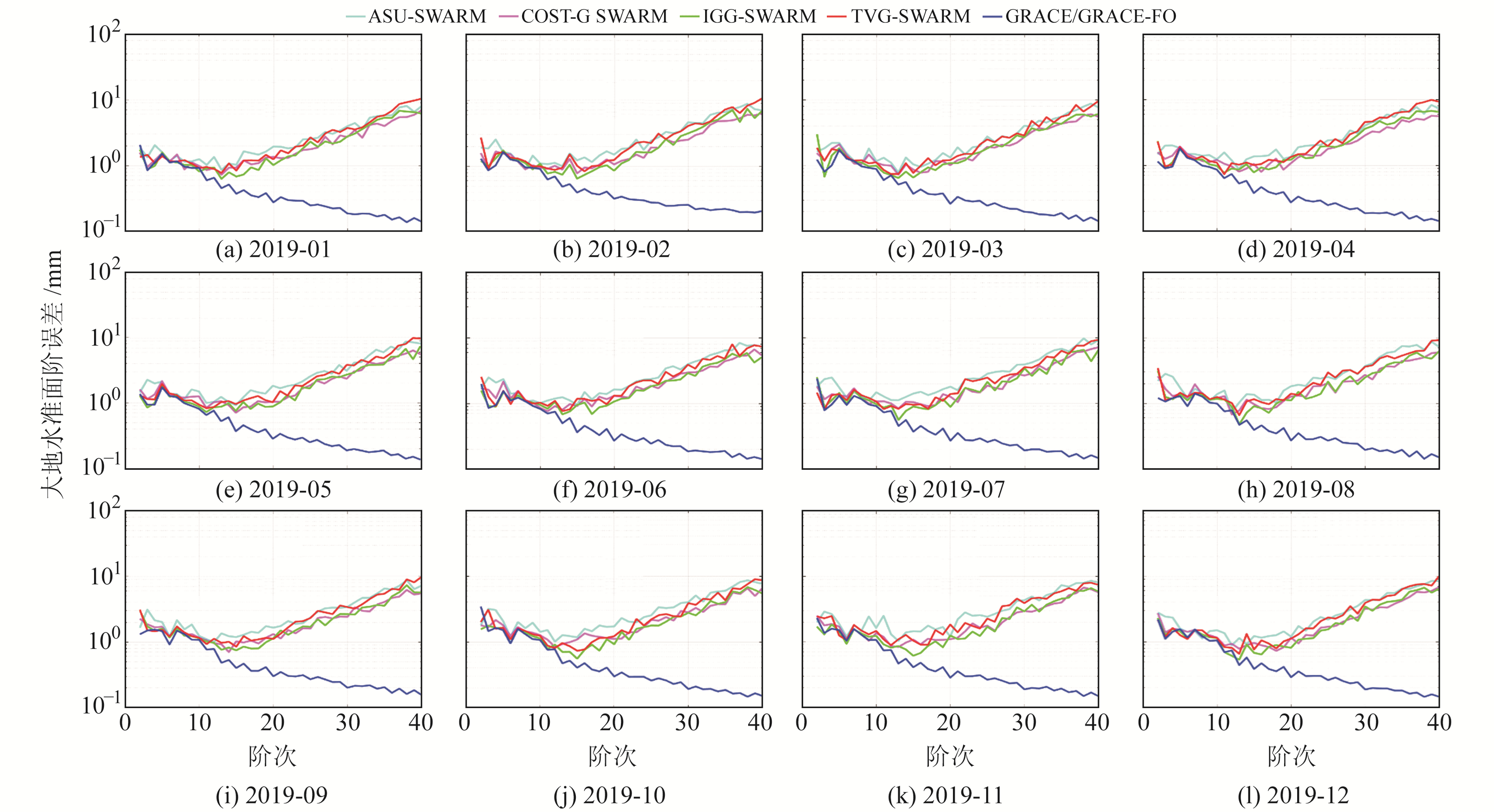
计算TVG-SWARM月时变重力场模型相对于EIGEN-6C4静态重力场模型的大地水准面阶误差,并与ASU、IGG与COST-G等科研机构解算的SWARM月时变重力场模型和ITSG-Grace2018/ITSG-Grace_op组合而成的月时变重力场模型(以下称为GRACE/GRACE-FO)结果进行比较,具体阶方差统计结果见图 1。
|
图 1 月时变重力场模型的阶方差 Fig. 1 The geoid degree error of monthly time-variable gravity field models |
通过图 1可知,本文解算的TVG-SWARM月时变重力场模型与其他SWARM月时变重力场模型的低阶项位系数的阶方差精度相当,特别是前10阶位系数的阶方差,不同SWARM月时变重力场模型结果均与GRACE/GRACE-FO月时变重力场模型结果较接近。TVG-SWARM月时变重力场模型前10阶位系数阶方差均值为1.422 mm,而ASU、COST-G、IGG和ITSG机构模型的对应均值分别为1.713 mm、1.426 mm、1.326 mm和1.229 mm,可见,TVG-SWARM月时变重力场模型前10阶位系数精度仅次于IGG-SAWRM与GRACE/GRACE-FO月时变重力场模型。不同SWARM月时变重力场模型与GRACE/GRACE-FO月时变重力场模型在10阶后的阶方差差异逐渐增大,这是因为SWARM月时变重力场模型高阶位系数的噪声更大。
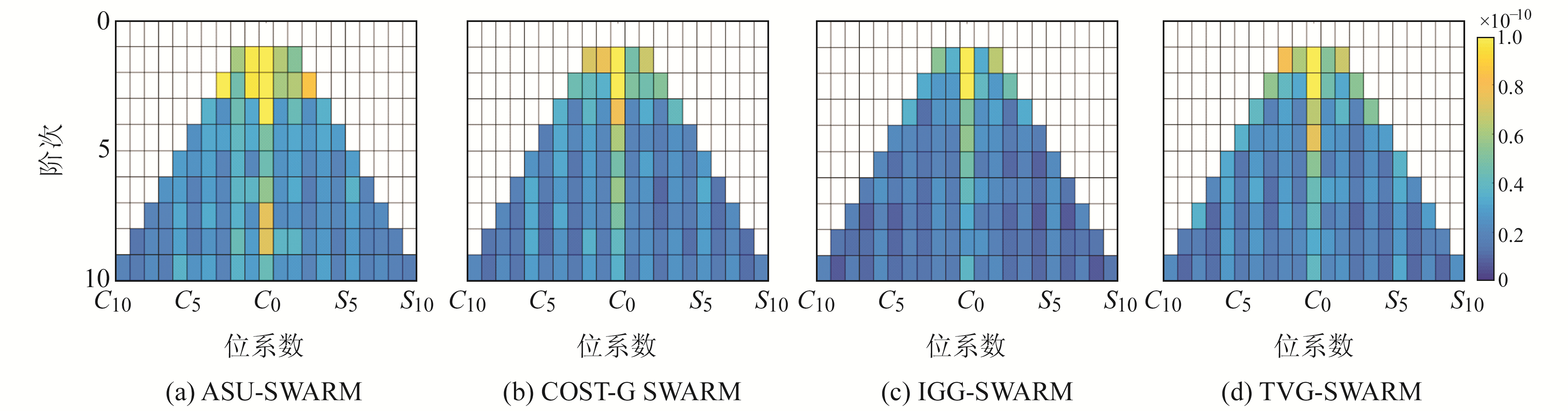
为进一步分析TVG-SWARM月时变重力场模型的解算精度,计算2015-01~2020-12不同机构的SWARM与GRACE/GRACE-FO月时变重力场模型前10阶次位系数的均方根误差(RMSE),得到相应位系数的误差谱,见图 2。由图可知,所有模型前10阶位系数的RMSE基本低于1.0×10-10,其中SWARM与GRACE/GRACE-FO月时变重力场模型的位系数差异主要集中在C20与C30处。综合图 2的各项误差谱看,IGG-SWARM月时变重力场模型前10阶位系数RMSE结果较优,TVG-SWARM与COST-G SWARM月时变重力场模型的位系数误差谱结果基本相当,ASU-SWARM月时变重力场模型结果最差。
|
图 2 月时变重力场模型位系数的误差谱 Fig. 2 Error spectra of spherical harmonic coefficients of monthly time-variable gravity field models |
由于SWARM与GRACE/GRACE-FO月时变重力场模型的最高阶次不同,为保证能够在同尺度条件下比较两者的反演结果,本文将后者截断至40阶,选取共同数据时段2015-01~2020-12,采用1 000 km的高斯滤波,其他数据处理流程和方法可参考文献[10-15]。
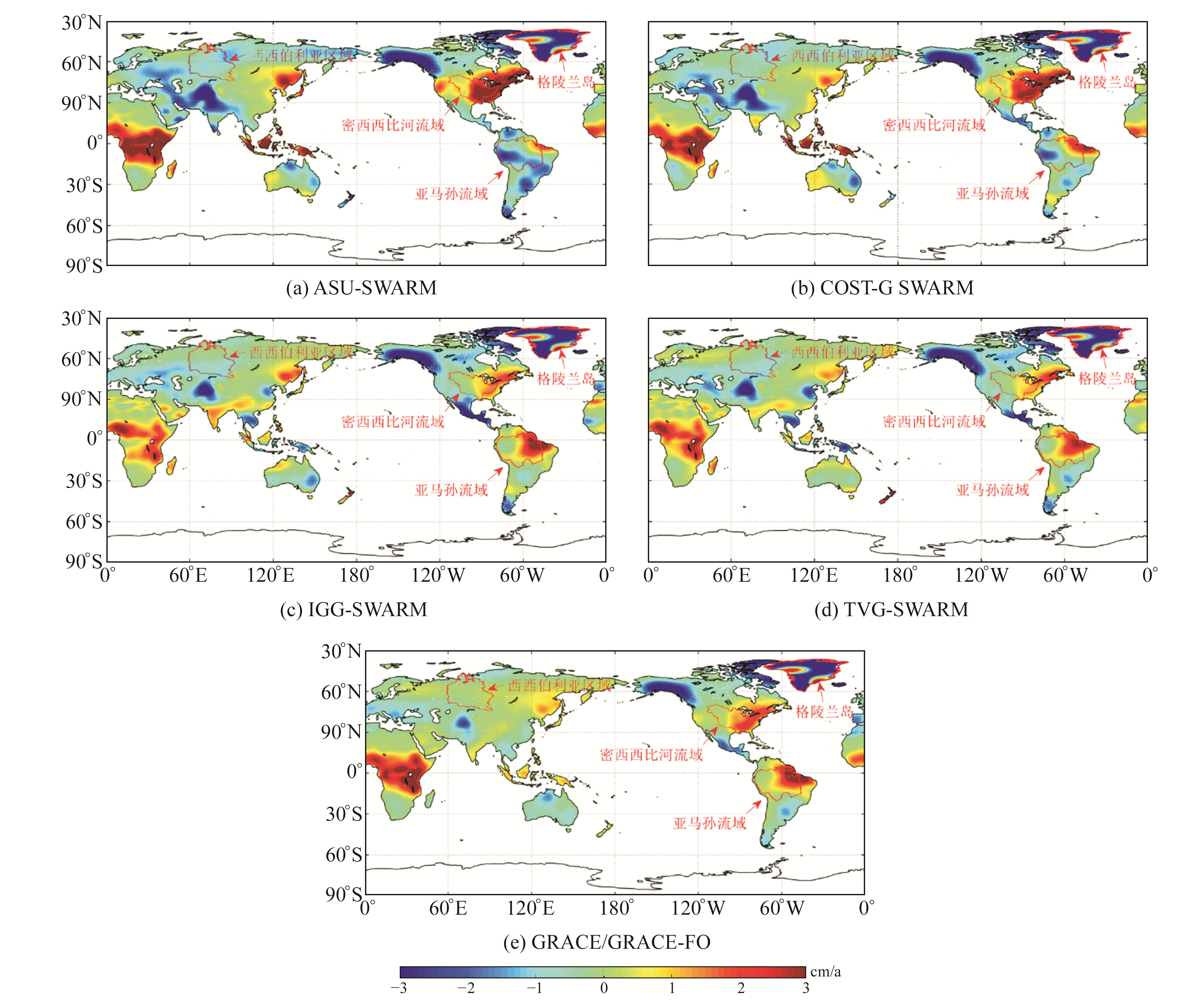
图 3给出不同SWARM与GRACE/GRACE-FO月时变重力场模型反演的全球等效水高的空间变化趋势。整体上看,两者在全球范围的陆地水储量变化趋势的空间分布具有较好的一致性。值得注意的是,TVG-SWARM与IGG-SWARM月时变重力场模型均由短弧积分法获得,两者的全球趋势图基本一致;TVG-SWARM与其他SWARM月时变重力场模型在南非洲、南美洲等区域存在一些差异,可能是由于采用的反演方法、背景场以及数据处理策略不同引起的。
|
图 3 全球陆地水储量变化趋势 Fig. 3 Trends of global terrestrial water storage change |
为了对模型反演精度进行更细致的分析,选取亚马孙流域、格陵兰岛、密西西比河流域和西西伯利亚区域为研究对象。从TVG-SWARM月时变重力场模型反演结果看出:1)格陵兰岛大部地区的冰盖质量逐年消减,密西西比河流域东南部出现水储量盈余,与其他月时变重力场模型反演结果的空间趋势高度一致;2)亚马孙流域东北部陆地水储量呈显著上升趋势,与IGG-SWARM和GRACE/GRACE-FO月时变重力场模型反演结果相吻合,而在流域西部等效水高的变化趋势与ASU-SWARM和COST-G SWARM月时变重力场模型相反;3)西西伯利亚区域南部的陆地水储量存在亏损,与IGG-SWARM月时变重力场模型反演结果较接近。整体而言,TVG-SWARM月时变重力场模型反演研究区域陆地水储量及冰盖质量的空间变化趋势与IGG-SWARM和GRACE/GRACE-FO月时变重力场模型的吻合度较高。
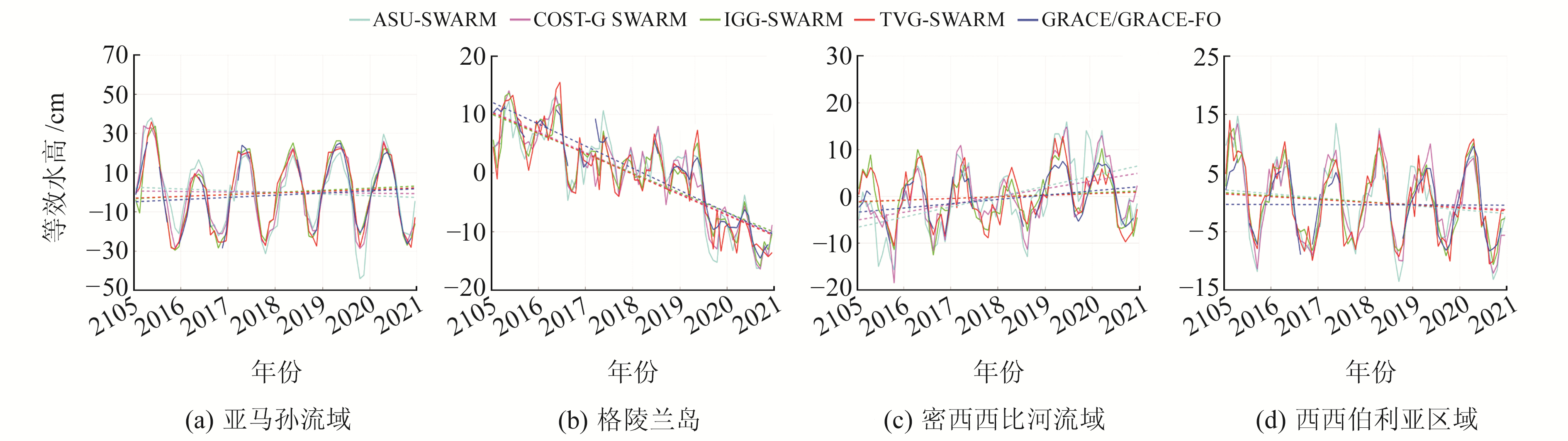
此外,利用不同SWARM与GRACE/GRACE-FO月时变重力场模型建立研究区域陆地水储量及冰盖质量变化的长期时间序列(图 4,图中虚线为各模型对应时间序列的周年趋势线),并统计各模型时间序列的周年趋势、趋势差值、RMSE和相关系数(表 2),进而分析TVG-SWARM月时变重力场模型在时间序列上的反演精度。
|
图 4 各区域等效水高的时间序列 Fig. 4 Time series of equivalent water height in each region |
|
|
表 2 各模型时间序列的周年趋势、趋势差值、RMSE和相关系数 Tab. 2 Annual trend, trend difference, RMSE and correlation coefficient of time series of each model |
综合图 4与表 2可得:1)不同SWARM与GRACE/GRACE-FO月时变重力场模型反演的亚马孙流域、密西西比河流域和西西伯利亚区域的等效水高在时间序列上均呈显著季节性变化,并反映格陵兰岛长期处于冰川消融状态。各SWARM与GRACE/GRACE-FO月时变重力场模型反演研究区域等效水高的周年变化趋势基本一致,其中TVG-SWARM与GRACE/GRACE-FO月时变重力场模型在上述区域的趋势差值分别为0.23 cm/a、0.57 cm/a、0.47 cm/a和0.27 cm/a,均优于ASU-SWARM月时变重力场模型结果。2)在RMSE方面,TVG-SWARM月时变重力场模型在亚马孙流域、密西西比河流域和西西伯利亚区域的RMSE分别达到4.27 cm、3.05 cm和2.73 cm,其与GRACE/GRACE-FO月时变重力场模型反演结果的一致性仅次于IGG-SWARM月时变重力场模型。在格陵兰岛,TVG-SWARM月时变重力场模型对应的RMSE为3.20 cm,与其他模型RMSE结果的最大差值仅为0.67 cm,说明不同SWARM月时变重力场模型的时间序列之间差异不大。3)对于相关系数,不同SWARM与GRACE/GRACE-FO月时变重力场模型在研究区具有极高的相关性,其中TVG-SWARM与GRACE/GRACE-FO月时变重力场模型的相关系数均达到0.85以上。
综上,利用TVG-SWARM月时变重力场模型探测陆地水储量及反演冰盖质量是可靠的。
3 结语本文基于短弧积分法,利用3颗SWARM卫星的精密轨道数据反演2015-01~2021-12共84个月的40阶次SWARM月时变重力场模型,并与ASU-SWARM、COST-G SWARM、IGG-SWARM与ITSG-GRACE/GRACE-FO等月时变重力场模型精度进行对比,结果表明:
1) 不同SWARM月时变重力场模型低阶项位系数的阶方差精度相当,其中前10阶结果均与GRACE/GRACE-FO月时变重力场模型相近,且不同SWARM与GRACE/GRACE-FO月时变重力场模型前10阶位系数的RMSE基本低于1.0×10-10。
2) 整体来看,不同SWARM月时变重力场模型在全球范围的陆地水储量变化趋势的空间分布与GRACE/GRACE-FO月时变重力场模型结果具有较好的一致性。在亚马孙流域、格陵兰岛、密西西比河流域和西西伯利亚区域中,本文模型与GRACE/GRACE-FO月时变重力场模型反演的区域等效水高的变化趋势一致,趋势差值分别为0.23 cm/a、0.27 cm/a、0.57 cm/a和0.47 cm/a,相关系数均达到0.85以上,两者的吻合情况良好,且本文模型与IGG-SWARM月时变重力场模型结果最接近。综合可得,本文TVG-SWARM月时变重力场模型精度是可靠的。后续将进一步开展本文模型与GRACE/GRACE-FO模型的融合研究。
| [1] |
汪秋昱, 饶维龙, 张岚, 等. GRACE时变重力信号反演方法研究的进展和展望[J]. 华中科技大学学报: 自然科学版, 2022, 50(9): 104-116 (Wang Qiuyu, Rao Weilong, Zhang Lan, et al. Progress and Prospect of GRACE Time-Varying Gravity Signal Inversion Method[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2022, 50(9): 104-116)
(  0) 0) |
| [2] |
陈智伟, 张兴福, 冉将军, 等. 利用新版GRACE时变模型反演珠江流域陆地水储量变化[J]. 大地测量与地球动力学, 2020, 40(3): 305-310 (Chen Zhiwei, Zhang Xingfu, Ran Jiangjun, et al. Terrestrial Water Storage Changes in Pearl River Region Derived from the Latest Release Temporal Gravity Field Models[J]. Journal of Geodesy and Geodynamics, 2020, 40(3): 305-310)
(  0) 0) |
| [3] |
Visser P, Doornbos E, Jose V, et al. Thermospheric Density and Wind Retrieval from Swarm Observations[J]. Earth, Planets and Space, 2013, 65(11): 1 319-1 331 DOI:10.5047/eps.2013.08.003
(  0) 0) |
| [4] |
Jäggi A, Dahle C, Arnold D, et al. Swarm Kinematic Orbits and Gravity Fields from 18 Months of GPS Data[J]. Advances in Space Research, 2016, 57(1): 218-233 DOI:10.1016/j.asr.2015.10.035
(  0) 0) |
| [5] |
Bezděk A, Sebera J, Teixeira J, et al. Time-Variable Gravity Fields Derived from GPS Tracking of Swarm[J]. Geophysical Journal International, 2016, 205(3): 1 665-1 669 DOI:10.1093/gji/ggw094
(  0) 0) |
| [6] |
Zehentner N, Mayer-Gürr T. Precise Orbit Determination Based on Raw GPS Measurements[J]. Journal of Geodesy, 2016, 90(3): 275-286 DOI:10.1007/s00190-015-0872-7
(  0) 0) |
| [7] |
Christina L, Jürgen K, Roelof R, et al. IGG-Swarm: Temporal Gravity Models from Swarm[EB/OL]. https://dataservices.gfz-potsdam.de/icgem/showshort.php?id=96be3fd8-7a9c-11ec-9fbb-f55ef7bbc29d, 2021
(  0) 0) |
| [8] |
Zhang X F, Chen Q J, Shen Y Z. Preliminary Monthly Gravity Field Models from Kinematic Orbits of SWARM Satellites[C]. EGU General Assembly, Vienna, 2021
(  0) 0) |
| [9] |
Mayer-Gürr T. Gravitationsfeldbestimmung aus der Analyse kurzer Bahnbögen am Beispiel der Satellitenmissionen CHAMP und GRACE[D]. Bonn: Institute für Theoretische Geodäsie der Universität Bonn, 2006
(  0) 0) |
| [10] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B12): 30 205-30 229 DOI:10.1029/98JB02844
(  0) 0) |
| [11] |
Sun Y, Riva R, Ditmar P. Optimizing Estimates of Annual Variations and Trends in Geocenter Motion and J2 from a Combination of GRACE Data and Geophysical Models[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(11): 8 352-8 370 DOI:10.1002/2016JB013073
(  0) 0) |
| [12] |
Cheng M K, Ries J C, Tapley B D. Variations of the Earth's Figure Axis from Satellite Laser Ranging and GRACE[J]. Journal of Geophysical Research: Solid Earth, 2011, 116(B1)
(  0) 0) |
| [13] |
Loomis B D, Rachlin K E, Wiese D N, et al. Replacing GRACE/GRACE-FO with Satellite Laser Ranging: Impacts on Antarctic Ice Sheet Mass Change[J]. Geophysical Research Letters, 2020, 47(3)
(  0) 0) |
| [14] |
Chambers D P, Wahr J, Tamisiea M E, et al. Ocean Mass from GRACE and Glacial Isostatic Adjustment[J]. Journal of Geophysical Research: Solid Earth, 2010, 115(B11)
(  0) 0) |
| [15] |
Landerer F W, Swenson S C. Accuracy of Scaled GRACE Terrestrial Water Storage Estimates[J]. Water Resources Research, 2012, 48(4)
(  0) 0) |
2. School of Civil and Transportation Engineering, Guangdong University of Technology, 100 West-Waihuan Road, Guangzhou 510006, China
 2023, Vol. 43
2023, Vol. 43
