2. 中国地震局地震大地测量重点实验室,武汉市洪山侧路40号,430071;
3. 湖北省地震局,武汉市洪山侧路48号,430071
微动台阵探测是从台阵采集的微动信号中提取瑞雷波频散曲线,反演得到地下介质横波速度结构的一种新兴天然源面波探测方法[1]。该方法具有抗干扰能力强、场地限制小、勘探耗时短等优势[2],在工程领域受到广泛关注[3-6]。利用微动进行二维剖面探测需要大量观测仪器,但仪器数量相对整个测线是有限的,为克服该难题,可开展滚动式数据采集,这种数据采集方式特别适合于因有建筑物等限制,通常只能沿交通公路采用线型台阵进行观测的城市区域[7]。同时,文献[8-9]将主动源面波多道分析(MASW)中共中心点成像的概念引入微动探测,提出共中心点(CMP)道集重组分析方法,可有效提高微动探测的效率和适用性,在城区浅层地质调查中具有较好的应用效果。
本文根据微动线型台阵高效滚动的观测特点与共中心点道集重组的基本原理,结合实践经验,设计一套适应于不同微动线型台阵的快速探测方案输出系统,并讨论不同参数下理论输出方案的特点,再通过城区具体场地进行实验观察,以分析其可行性和有效性。
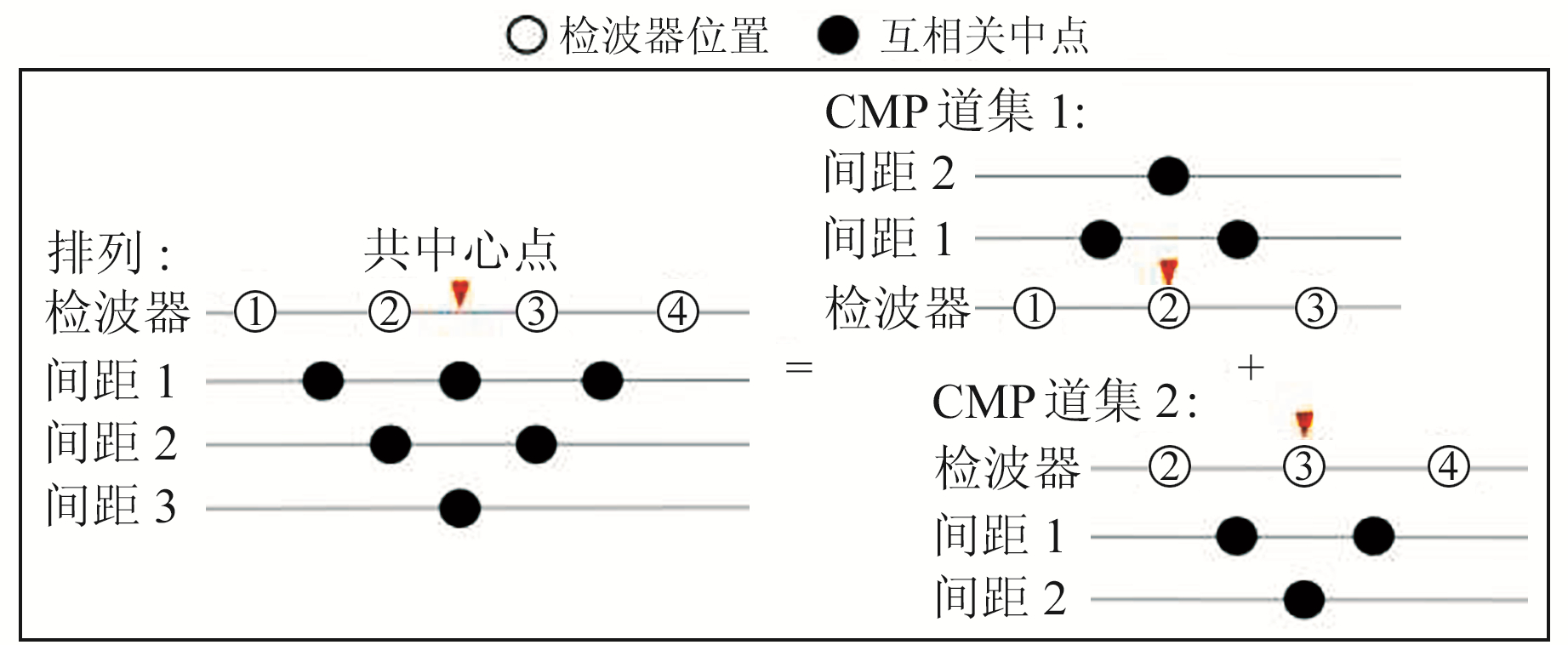
1 方案设计 1.1 基本原理本文方案设计原理如图 1所示,图中空心圆为检波器位置,实心圆为互相关中点,共中心点(CMP)为用于计算互相关的检波器对中点位置。通常1个排列中检波器自相关计算仅得到1个共中心测点;道集重组后,检波器1、2、3组成的CMP道集1和检波器2、3、4组成的CMP道集2可分别进行自相关计算,得到2个测点。
|
图 1 共中心点道集重组分析概念图 Fig. 1 Conceptual diagram of common midpoint(CMP) gather rearrangement analysis |
对每组CMP道集采用SPAC法提取频散曲线。假设微动在时空上符合平稳随机过程,且以基阶面波为主,经初步计算,微动记录f、g的相关系数COHf, g(ω, r)为:
| $ \mathrm{COH}_{f, g}(\omega, r)=\frac{\operatorname{Re}\left(\mathrm{CC}_{f, g}(\omega, r)\right)}{\sqrt{A_{f}(\omega) \cdot A_{g}(\omega)}} $ | (1) |
式中,ω为角频率,r为检波器对间距,Af(ω)和Ag(ω)分别为f和g的自功率谱,CCf, g(ω, r)为f和g的互功率谱,Re(·)为取复数实部。对f和g的相关系数方位平均后得到空间自相关系数SPACf, g(ω, r),其计算公式为:
| $ \text{SPAC}_{f, g}(\omega, r)=\frac{1}{2 {\rm{ \mathsf{ π}}}} \int_{0}^{2 {\rm{ \mathsf{ π}}}} \mathrm{COH}_{f, g}(\omega, r) \mathrm{d} \varphi $ | (2) |
式中,φ为方位角。将空间自相关系数拟合第一类零阶Bessel函数,最小误差ε为:
| $ \varepsilon=\sqrt{\frac{\sum\limits_{i=1}^{m}\left(\operatorname{SPAC}_{f, g}(\omega, r)-J_{0}\left(\frac{\omega, r}{c(\omega)}\right)\right)_{i}^{2}}{m}} $ | (3) |
式中,J0(·)为第一类零阶Bessel函数,c(ω)为瑞雷波相速度,m为检波器对个数。
1.2 参数及流程已知检波器总数为Q,目标探测深度为H,横向探测精度为D,理论探测长度为Xg。1个排列中包括多组CMP道集,每组CMP道集中参与空间自相关计算的道数(即分组道数)为a,台间距为d,测点数为b。规定测线前进方向为前方,第1次排列结束后依次移动后方N道至测线前方,沿测线如此重复滚动n次,完成(n+1)个排列,可得到总测点数S、实际探测长度X、仪器布设里程L和预估探测总用时T。
根据野外观测及工程实践经验:1)目标探测深度约为最大计算距离的5倍,最大计算距离指CMP道集中自相关计算中心与最远检波器的距离;2)1次排列同步采集时长为30 min,单次移台损失时长约为10 min。为保证数据质量,通常采集时长不小于15 min,周围环境有明显干扰时可适当延长观测时间;数据采集所用仪器集成度高、轻量便携,单次移台损失时间仅依据台阵规模和作业人数来确定,一般为5~10 min。
参数计算流程如图 2所示,其中d=D表示横向探测精度(测点距)和台间距相等,便于台阵布设和校验;

|
图 2 参数计算流程 Fig. 2 Flowchart of parameter calculation |
|
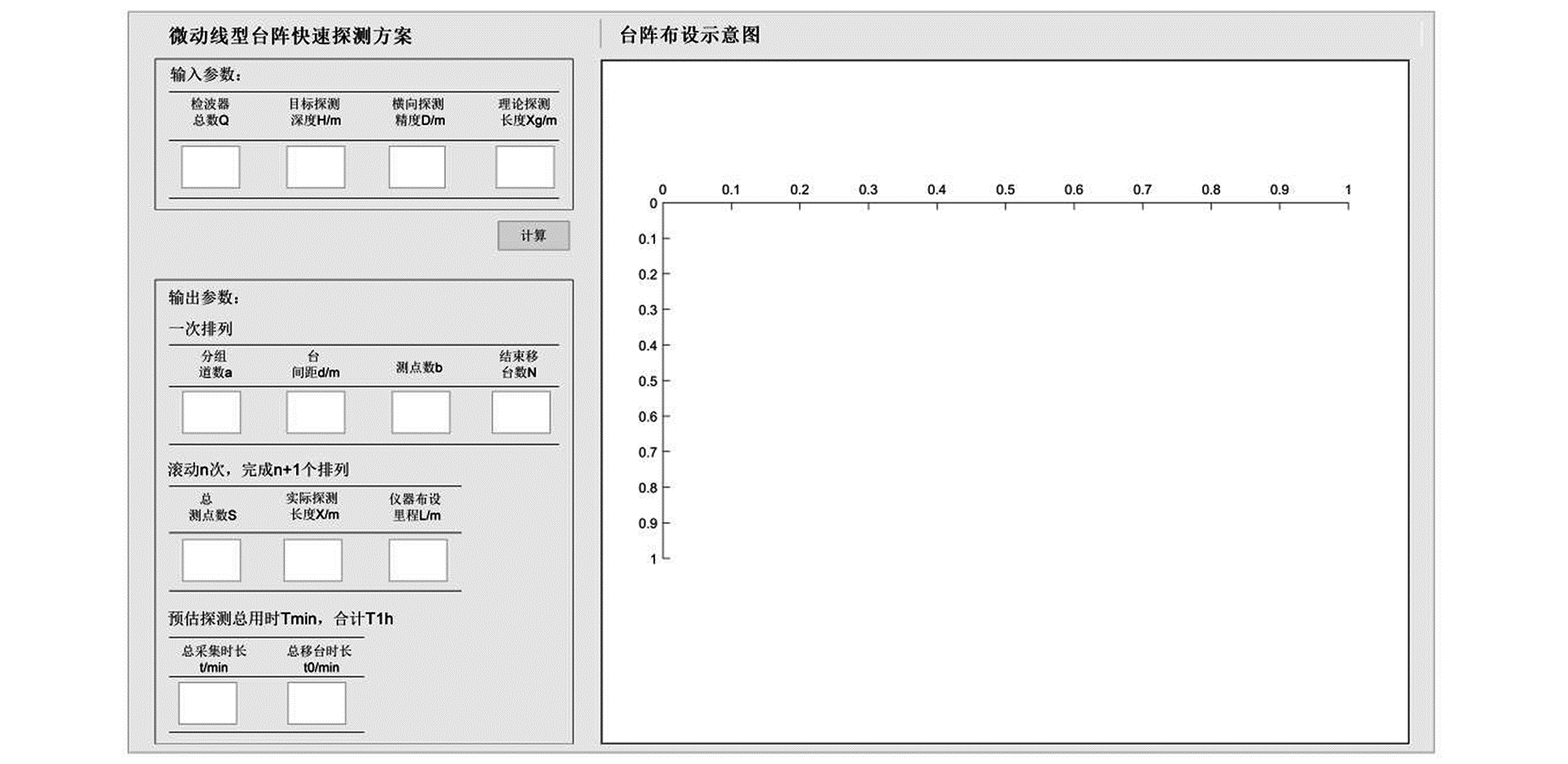
图 3 方案输出系统界面 Fig. 3 Interface of scheme output system |
城区浅层探测一般布设半径数米至数十米的小型台阵,探测深度在100 m以内[10]。结合城市微动探测特点和仪器配置情况,将检波器总数16台、目标探测深度100 m、横向探测精度(测点距)5 m、理论探测长度200 m作为城市道路浅层探测常规方案的输入参数,并以此为基准,对比不同参数理论输出方案的特点、优势或注意事项。
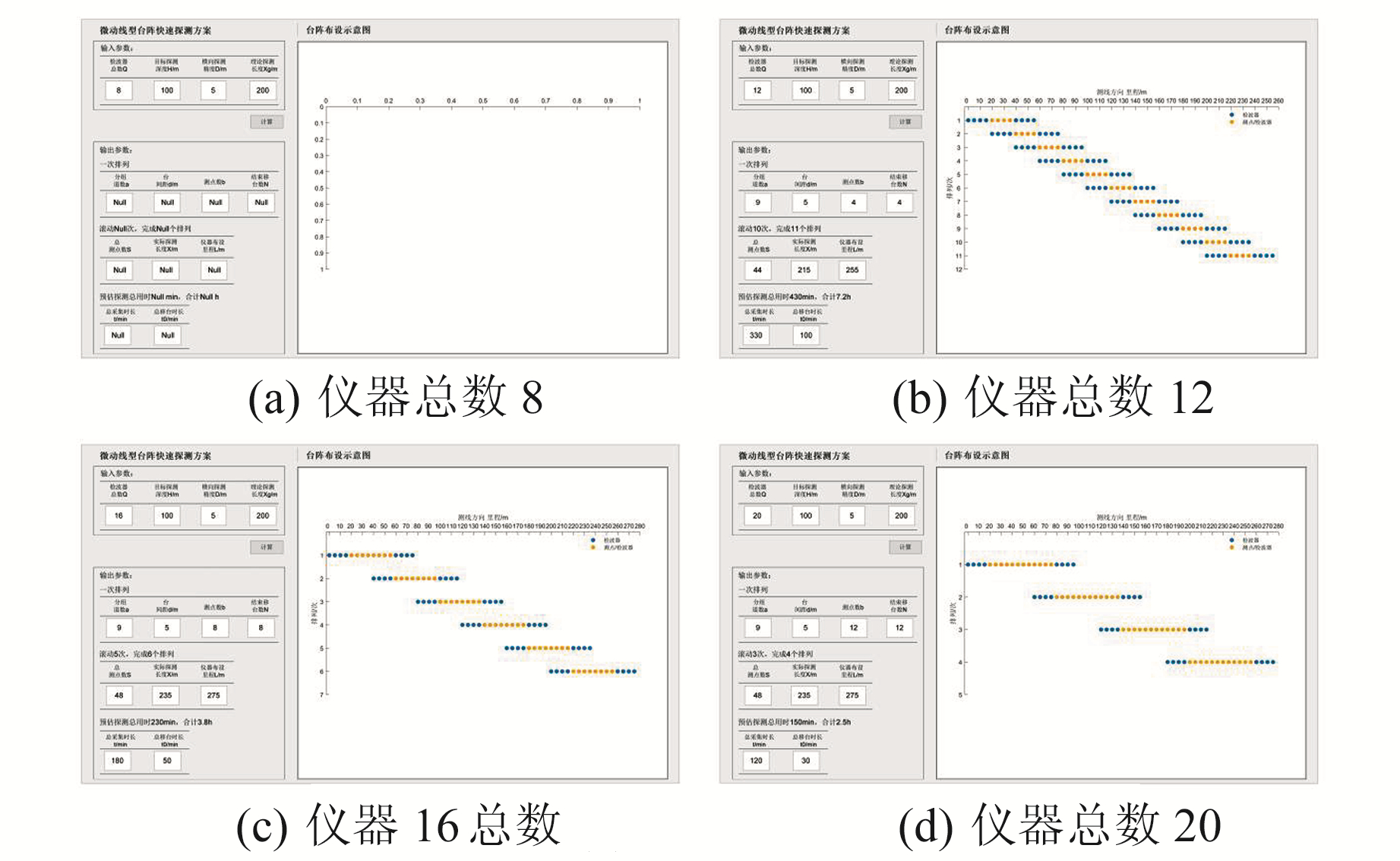
1.3.1 不同检波器总数结合图 4和表 1可知,仪器数量小于单测点空间自相关计算所需道数时,输出方案无效;而针对有效探测方案,随着检波器总数增加,分组道数相等,总测点数及实际探测长度基本不变,排列个数及探测用时显著减少,探测效率大大提高。
|
图 4 不同检波器总数的输出方案 Fig. 4 Output scheme for different number of geophones |
|
|
表 1 不同检波器总数的输出方案对比 Tab. 1 Comparison of output scheme for different number of geophones |
结合图 5和表 2可知,目标测深超出5倍最大计算距离时,输出方案无效;针对有效探测方案,随着探测目标深度增大,总测点数及实际探测长度基本保持不变,分组道数、排列个数及探测总用时显著增加。值得注意的是,目标深度过浅导致分组道数减少,可能引起测点频散成像的分辨率下降,实际观测中应予以考虑。

|
图 5 不同目标探测深度的输出方案 Fig. 5 Output scheme for different target detection depths |
|
|
表 2 不同目标探测深度的输出方案对比 Tab. 2 Comparison of output scheme for different target detection depths |
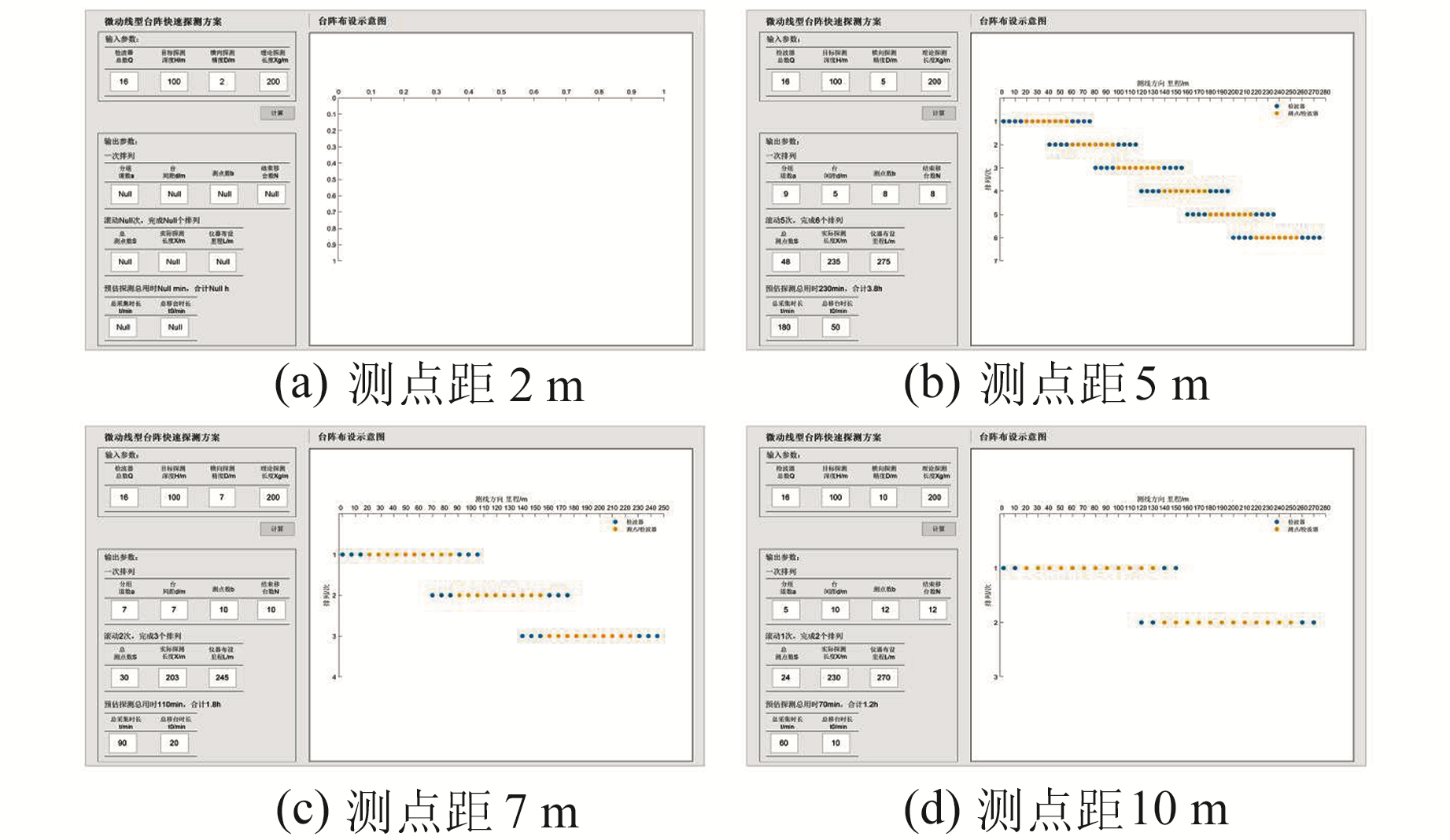
结合图 6和表 3可知,当测点距过小、探测深度较浅时,为达到目标测深,需更多检波器参与自相关计算,致使超出仪器总数,输出方案无效;针对有效探测方案,随着横向精度(测点距)增加,分组道数、排列个数及总测点数减少,相应的总探测耗时减小,实际探测长度不随测点距发生显著改变。横向精度(测点距)过大虽能正常输出方案,但对应分组道数减小可能导致测点频散成像的分辨率下降,实际观测中应予以考虑。
|
图 6 不同横向探测精度的输出方案 Fig. 6 Output scheme for different lateral detection accuracy |
|
|
表 3 不同横向探测精度的输出方案对比 Tab. 3 Comparison of output scheme for different lateral detection accuracy |
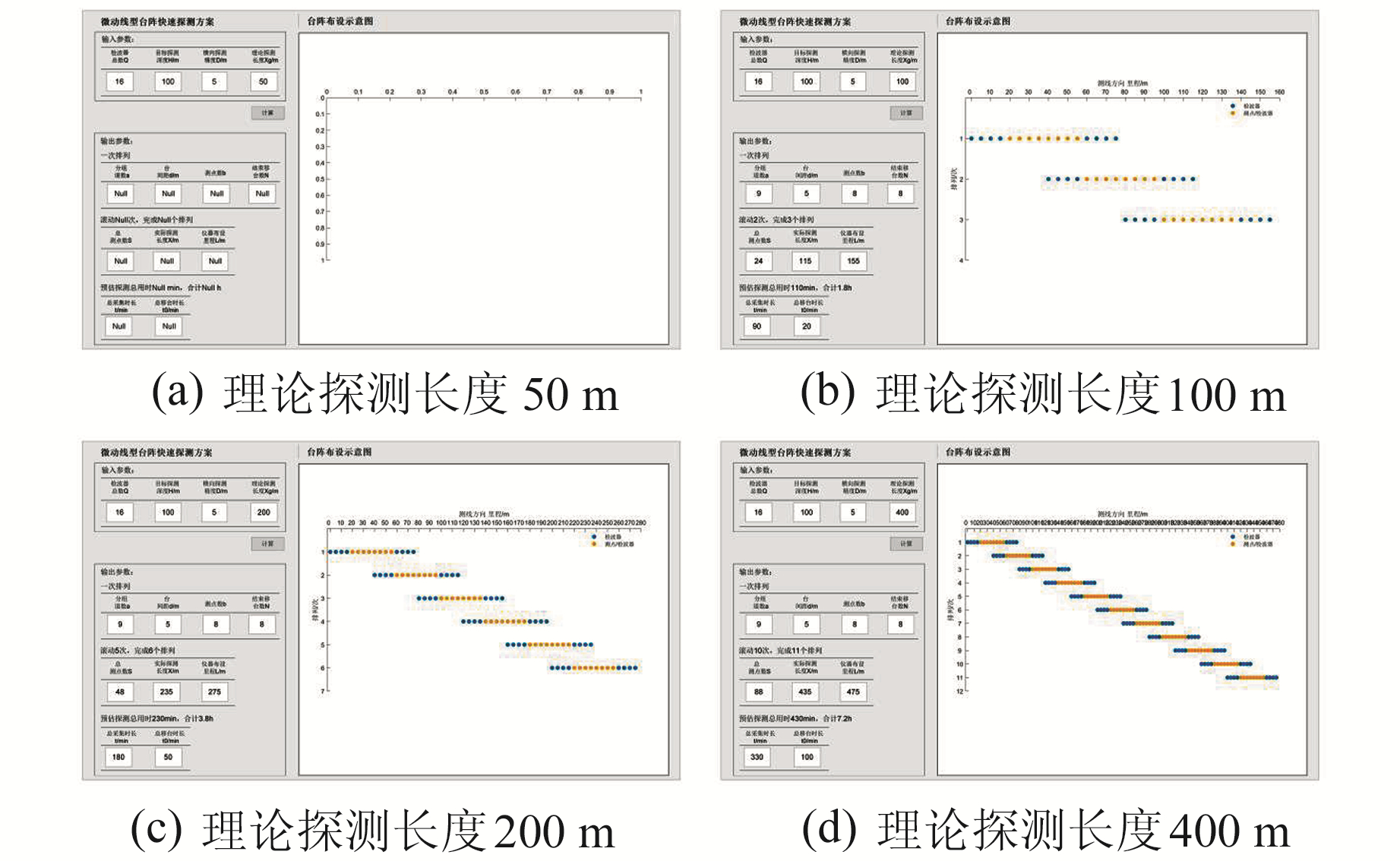
结合图 7和表 4可知,理论探测长度小于1个排列长度时,无需台阵平移,输出方案无效;针对有效探测方案,随着理论探测长度增加,分组道数不变,频散分辨率不变,但排列个数、总测点数及总用时呈线性增加,相应的工作量增大,实际探测长度趋近于理论值。
|
图 7 不同理论探测长度的输出方案 Fig. 7 Output scheme for different theoretical detection length |
|
|
表 4 不同理论探测长度的输出方案对比 Tab. 4 Comparison of output scheme for different theoretical detection length |
选取武汉市中心城区某沥青道路(30.541°N,114.346°E)作为实验观测场地(图 8),场地总长80 m,可探测长约60 m,路面平整,周边区域道路纵横、建筑密布、车流量大,天然源较为丰富。

|
图 8 实验场地 Fig. 8 Experimental site |
实验采用节点式UGL-3C检波器,该设备集成度高、性能较好。UGL-3C记录通道数为3道,固有频率为4.5 Hz,内置GPS自动授时可保证台站间时间同步性。选定采样率为250 Hz,台站有效同步观测时间不小于30 min。实验开始前将16台仪器加装三角锥,增强与地面耦合,并进行一致性检测(图 9),结果表明,在有效频段(1~25 Hz)内仪器的一致性较好,符合微动探测要求。

|
图 9 一致性检测结果 Fig. 9 Consistency test results |
数据采集时,采用与检波器匹配的UGL-3C探测系统,该系统由主设备、路由站和检波器组成[11],其优势在于:1)自动识别仪器编号与台阵序号并进行配置;2)实时监测数据采集质量并显示各节点工作状态;3)人为发送控制指令启动采集且数据通过Wi-Fi无线传输至主设备,能很好地配合实验数据采集。
本文数据采集观测方案由微动线型台阵快速探测方案程序给出。由方案分析可知,检波器总数越多探测越高效,因此将全部16台检波器均用于观测;在有限长场地实现排列多次滚动观测分析,确定探测深度为40 m,重点考虑横向探测精度(测点距)。由图 10可知,当测点距为1 m时,仪器数量过少,不足以达到预估探测深度;当测点距为3 m时,台站布设里程为105 m,超出场地总长,不符合要求;当测点距为4 m时,1次排列就有60 m,无法实现连续滚动观测;而当测点距为2 m时,在该实验场地可滚动观测3次,完成4次排列,实际探测长度为62 m,仪器布设里程为78 m,符合场地要求。

|
图 10 现场实验输出方案 Fig. 10 Output scheme of field experiment |
为提高数据质量,减小近源干扰,实验选在05:00~07:00时段进行。首先沿测线将所有检波器按2 m台间距依次布设,并通过Wi-Fi路由站连接至主设备;然后设置台间距、分组道数等排列所需参数,启动采集;采集中检波器状态信息和瑞雷波垂直分量数据可无线传输至主设备,在此过程中可实时监控各位置测点的完成进度;30 min后第1次排列采集结束,最终获得8个测点格式为SG2的数据文件,包含台阵中台站的相对位置信息和波形数据。第1次排列数据采集过程如图 11所示。

|
图 11 第1次排列数据采集过程 Fig. 11 Data acquisition process in the first array |
第1次排列采集结束后,按图 10(b)所示观测方案,将后方8台检波器移至测线最前方对应台站位置,进行下1次排列的数据采集,依次循环向前滚动3次,共完成4次排列,得到32个测点数据。在此过程中,通过主设备可一键设定坐标并启动采集,仅需保证移台时检波器位置准确,可节省记录坐标和等待授时的时间。采集结束后,整条测线共得到32个实际测点,探测长度为62 m,与理论参数一致,实际用时约2.5 h,与预估时长相符。
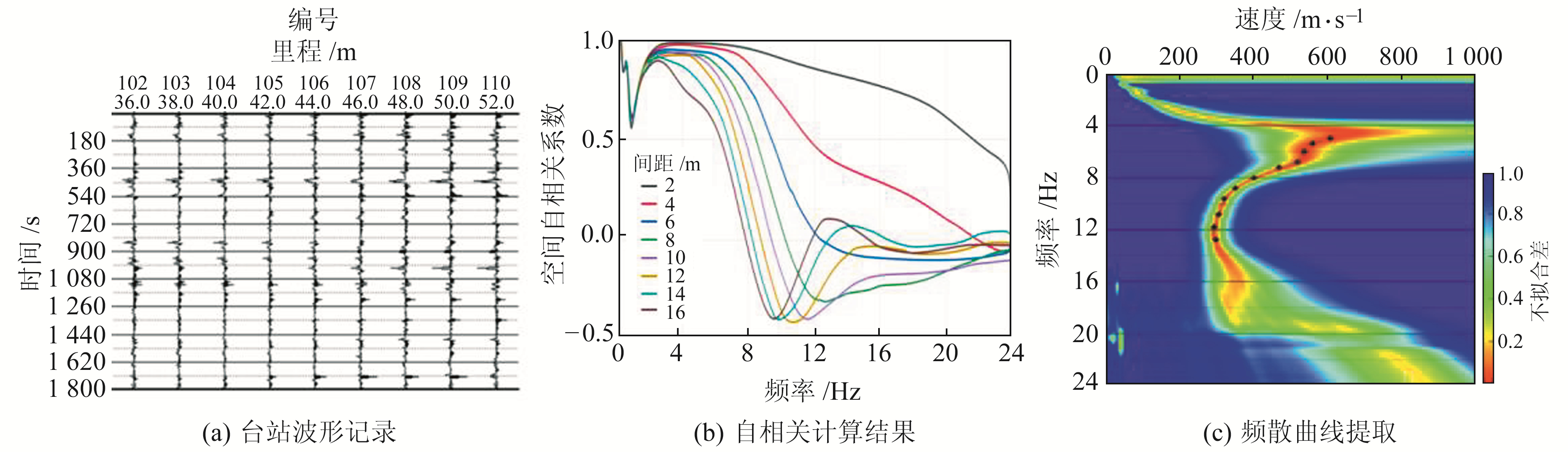
2.3 数据处理在数据采集过程中已将截取和解编的测点数据以SG2格式文件通过Wi-Fi无线传输至主设备。对于单测点,仅需读取CMP道集中带有坐标及时长等参数的台站波形记录(图 12(a)),经滤波、去均值及去倾斜等预处理后即可计算出各台站对空间自相关系数,拟合不同间距台站对空间自相关系数(图 12(b))与第一类零阶Bessel函数单调递减部分,得到测点频散谱(图 12(c))。
|
图 12 实测频散曲线提取过程 Fig. 12 Extraction process of measured dispersion curve |
对于城区浅层地下空间结构探测,通常仅需了解地层剖面速度的相对变化,利用式(4)计算一维视横波速度,可避免反演多解性,较快地反映地层速度的相对变化[12]:
| $ v_{x, i}=\left(\frac{t_{i} v_{r, i}^{4}-t_{i-1} v_{r, i-1}^{4}}{t_{i}-t_{i-1}}\right)^{\frac{1}{4}} $ | (4) |
式中,vx, i为第i个频率值的视横波速度,vr, i为第i个频率值的瑞雷波速度,ti为对应频率值的周期。依次循环计算32个测点的频散曲线,再运用克里金插值法进行横向插值,即可快速获得横向精度为2 m的微动二维视横波速度剖面(图 13)。

|
图 13 二维视横波速度剖面 Fig. 13 2D apparent S-wave velocity profile |
微动线型台阵探测具有抗干扰性强、场地限制小、勘探耗时短的特点,在城市地层勘探方面具有较大优势。通过研究微动线型台阵快速探测方案,能够根据场地条件和设计要求确定主要采集参数,制定合理观测方式,提高外业观测效率,为台阵布设和平移提供参考,适用于城市浅地表、长距离、高精度勘探。
微动线型台阵快速探测方案可借助高集成探测系统(如UGL-3C)实现实时监控、无线传输及自动截取等功能,后期可进一步优化探测过程,使该方案具有更高的应用价值,以满足城区浅层微动精细化和快速化探测需求。
| [1] |
Okada H, Suto K. The Microtremor Survey Method[M]. Tulsa: Society of Exploration Geophysicists, 2003
(  0) 0) |
| [2] |
李万伦, 刘素芳, 田黔宁, 等. 城市地球物理学综述[J]. 地球物理学进展, 2018, 33(5): 2 134-2 140 (Li Wanlun, Liu Sufang, Tian Qianning, et al. Reviews in Urban Geophysics[J]. Progress in Geophysics, 2018, 33(5): 2 134-2 140)
(  0) 0) |
| [3] |
徐佩芬, 李传金, 凌甦群, 等. 利用微动勘察方法探测煤矿陷落柱[J]. 地球物理学报, 2009, 52(7): 1 923-1 930 (Xu Peifen, Li Chuanjin, Ling Suqun, et al. Mapping Collapsed Columns in Coal Mines Utilizing Microtremor Survey Methods[J]. Chinese Journal of Geophysics, 2009, 52(7): 1 923-1 930)
(  0) 0) |
| [4] |
徐佩芬, 侍文, 凌甦群, 等. 二维微动剖面探测"孤石": 以深圳地铁7号线为例[J]. 地球物理学报, 2012, 55(6): 2 120-2 128 (Xu Peifen, Shi Wen, Ling Suqun, et al. Mapping Spherically Weathered "Boulders" Using 2D Microtremor Profiling Method: A Case Study along Subway Line 7 in Shenzhen[J]. Chinese Journal of Geophysics, 2012, 55(6): 2 120-2 128)
(  0) 0) |
| [5] |
杜亚楠, 徐佩芬, 凌甦群. 土石混合滑坡体微动探测: 以衡阳拜殿乡滑坡体为例[J]. 地球物理学报, 2018, 61(4): 1 596-1 604 (Du Yanan, Xu Peifen, Ling Suqun. Microtremor Survey of Soil-Rock Mixture Landslides: An Example of Baidian Township, Hengyang City[J]. Chinese Jour-nal of Geophysics, 2018, 61(4): 1 596-1 604)
(  0) 0) |
| [6] |
沈雨忆, 李井冈, 王秋良, 等. 基于SPAC法勘探武汉市江夏区地下岩溶结构[J]. 大地测量与地球动力学, 2018, 38(5): 482-486 (Shen Yuyi, Li Jinggang, Wang Qiuliang, et al. Application of SPAC Method to Probe Underground Karst Structure in Jiangxia District, Wuhan[J]. Journal of Geodesy and Geodynamics, 2018, 38(5): 482-486)
(  0) 0) |
| [7] |
周紫岩, 廖武林, 李井冈. 微动线型台阵数据快速处理研究[J]. 大地测量与地球动力学, 2020, 40(10): 1 097-1 100 (Zhou Ziyan, Liao Wulin, Li Jinggang. Microtremor Survey Method Linear Array Rapid Processing[J]. Journal of Geodesy and Geodynamics, 2020, 40(10): 1 097-1 100)
(  0) 0) |
| [8] |
Hayashi K, Craig M, Kita T, et al. CMP Spatial Autocorrelation Analysis of Multichannel Passive Surface-Wave Data[C]. SEG Annual Meeting, New Orleans, 2015
(  0) 0) |
| [9] |
Tan S J, Hayashi K, He B, et al. Active Fault Investigation by 3D Ambient Noise Tomography in Hebei Province, China[C]. SEG Annual Meeting, San Antonio, 2019
(  0) 0) |
| [10] |
贾辉, 陈义军, 王铁领, 等. 浅部地层微动勘探关键影响因素探讨[J]. 工程勘察, 2018, 46(9): 68-73 (Jia Hui, Chen Yijun, Wang Tieling, et al. Key Factors of Shallow Stratum Micro-Tremor Exploration[J]. Geotechnical Investigation and Surveying, 2018, 46(9): 68-73)
(  0) 0) |
| [11] |
吴海超, 林君, 李哲, 等. 无缆存储式地震仪无线网络监控技术[J]. 吉林大学学报: 工学版, 2012, 42(5): 1 296-1 301 (Wu Haichao, Lin Jun, Li Zhe, et al. Wireless Network Monitoring Technology of Cable-Less Stored Seismic Instrument[J]. Journal of Jilin University: Engineering and Technology Edition, 2012, 42(5): 1 296-1 301)
(  0) 0) |
| [12] |
Xu P F, Ling S Q, Li C J, et al. Mapping Deeply-Buried Geothermal Faults Using Microtremor Array Analysis[J]. Geophysical Journal International, 2012, 188(1): 115-122
(  0) 0) |
2. Key Laboratory of Earthquake Geodesy, CEA, 40 Hongshance Road, Wuhan 430071, China;
3. Hubei Earthquake Agency, 48 Hongshance Road, Wuhan 430071, China
 2023, Vol. 43
2023, Vol. 43


