接收机自主完好性监测算法具有低成本、自主性和灵活性等特点,其利用接收机内部的冗余信息对卫星测量值进行一致性校验,当接收机发生故障或无法提供导航服务时,向用户发出告警信息[1]。目前比较常用的RAIM算法为仅利用当前伪距观测量的“快照(snapshot)”方法,包括伪距比较法[2]、最小二乘残差法[3]和奇偶矢量法[4],这些方法均只需要一个历元的观测量就可以进行故障探测和识别。陈柯勋等[5]提出一种根据卫星故障检测难度动态分配漏检率的方法;杨传森等[6]利用最大定位误差的完好性风险,使残差更精确和数据可靠性更高;舒宝等[7]基于卫星特征斜率加权优化故障检测统计量,可较好地解决高漏检风险卫星在故障检测中不敏感的问题;陈小平等[8]基于最小二乘残差故障检测,引入调整系数来降低漏检率;Yang等[9]深入讨论总体最小二乘残差在RAIM算法中的应用。
虽然RAIM算法故障检测可以通过提高检验门限来降低漏检率,但同时也会增大误警率,且检验门限的选取涉及到权衡误警率和漏检率之间的关系;最小二乘残差法未考虑到最小二乘存在矩阵病态的问题,因此一次性排除所有故障卫星会存在缺陷。针对上述问题,本文提出一种改进的RAIM算法,通过引入卫星定位内符合精度检验门限,并对最小二乘残差法的故障识别流程进行改进,同时给出相应算例结果。
1 RAIM算法原理 1.1 RAIM算法基本模型通常GNSS伪距观测模型可表示为:
| $ \boldsymbol{y}=\boldsymbol{H x}+\boldsymbol{\varepsilon} $ | (1) |
式中,y∈Rn×1表示伪距观测值与计算伪距之差的n维矢量,n为可见卫星数; H∈Rn×4为待估参数的系数矩阵;x∈R4×1为待估参数矢量;ε∈Rn×1为伪距观测噪声矢量。
用户状态的最小二乘解为:
| $ \hat{\boldsymbol{x}}=\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{y} $ | (2) |
式中,矩阵P为伪距观测权阵。
伪距残差矢量v可表示为:
| $ \begin{gathered} \boldsymbol{v}=\boldsymbol{y}-\hat{\boldsymbol{y}}=\left(\boldsymbol{I}-\boldsymbol{H}\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{P}\right) \boldsymbol{y}= \\ \left(\boldsymbol{I}-\boldsymbol{H}\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{P}\right) \boldsymbol{\varepsilon} \end{gathered} $ | (3) |
伪距残差矢量的协因数阵Qv可表示为:
| $ \boldsymbol{Q}_{v}=\boldsymbol{P}^{-1}-\boldsymbol{H}\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} $ | (4) |
验后单位权中误差σ由伪距残差平方和(SSE)计算得到:
| $ \sigma=\sqrt{\boldsymbol{v}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{v} /(n-4)}=\sqrt{\mathrm{SSE} /(n-4)} $ | (5) |
若伪距误差矢量ε中的各个分量是相互独立的正态分布随机误差,均值为0,方差为σ02,可作二元假设:H0(无故障):E(ε)=0,则SSE/σ02~χ2(n-4);H1(有故障):E(ε)≠0,则SSE/σ02~χ2(n-4, λ)。
给定误警率PFA,有下列概率等式成立:
| $ \begin{gathered} P\left(\mathrm{SSE} / \sigma_{0}^{2}<T^{2}\right)= \\ \int_{0}^{T^{2}} f_{\chi^{2}(n-4)}(x) \mathrm{d} x=1-P_{\mathrm{FA}} \end{gathered} $ | (6) |
可通过式(6)确定检验门限T,并计算出验后单位权中误差σ的检验门限σT=σ0×T/
通常利用水平保护级(horizontal protection level, HPL)来判断卫星几何条件是否满足需求。令A=(HTPH)-1HT,可以证明有如下关系式成立[10]:
| $ \frac{A_{1 i}^{2}+A_{2 i}^{2}}{Q_{v_{i i}}}=\mathrm{HDOP}_{i}-\mathrm{HDOP} $ | (7) |
式中,HDOP表示所有观测卫星参与计算的水平精度衰减因子;HDOPi表示去掉第i颗卫星后剩余卫星计算的水平精度因子。
给定漏检概率PMD,满足以下概率等式:
| $ \begin{gathered} P\left(\mathrm{SSE} / \sigma_{0}^{2}<T^{2}\right)= \\ \int_{0}^{T^{2}} f_{\chi^{2}(n-4, \lambda)}(x) \mathrm{d} x=P_{\mathrm{MD}} \end{gathered} $$ $ | (8) |
由式(8)可求得非中心化参数λ。δHDOPi=HDOPi-HDOP为水平精度衰减因子变化,取其最大值为δHDOPmax,则水平保护级HPL计算公式为:
| $ \mathrm{HPL}=\delta \mathrm{HDOP}_{\max } \times \sigma_{0} \times \sqrt{\lambda} $ | (9) |
基于最小二乘残差矢量构造统计量:
| $ d_{i}=\frac{\left|v_{i}\right|}{\sigma_{0} \sqrt{Q_{v_{i i}}}} $ | (10) |
对统计量di作二元假设:H0(无故障):E(εi)=0,则di~N(0, 1);H1(有故障):E(εi)≠0,则di~N(δi, 1)。
给定总体误警概率PFA,则每个统计量的误警概率为PFA/n,有如下等式成立:
| $ \begin{gathered} P\left(d>T_{d}\right)= \\ \frac{2}{\sqrt{2 {\rm{ \mathsf{ π}}}}} \int_{T_{d}}^{\infty} \mathrm{e}^{-\frac{x^{2}}{2}} \mathrm{~d} x=P_{\mathrm{FA}} / n \end{gathered} $ | (11) |
通过式(11)可求得检验门限Td,将每颗卫星的检验统计量di与检验门限Td比较,如果di>Td,则表明第i颗卫星出现故障,应将其剔除。
2 改进的RAIM算法传统的RAIM算法故障检测方法完全依赖于伪距残差平方和,而有时伪距残差并不能正确反映出卫星定位偏差,从而导致完好性监测算法漏检率过高。内符合精度通过数据间的离散度反应数据质量的好坏,一般可用方差或标准差来度量。通过计算卫星定位内符合精度,可判断当前卫星位置解的离散程度,通常当卫星观测值质量较差时,卫星位置解也较为分散。
按协因数传播率,待估参数x的协因数阵Qx可由下式计算得到:
| $ \begin{gathered} \boldsymbol{Q}_{x}=\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{P H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{Q} \boldsymbol{P H}\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{H}\right)^{-1}= \\ \left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{H}\right)^{-1} \end{gathered} $ | (12) |
则待估参数各分量的中误差Vci可表示为:
| $ V_{c_{i}}=\sigma \times Q_{x_{i i}} $ | (13) |
内符合精度检验统计量d可表示为:
| $ d=\sqrt{\sigma_{h}^{2}+\sigma_{z}^{2}+\sigma_{t}^{2}} $ | (14) |
式中,σh2为水平方向定位结果的方差,σz2为垂直方向定位结果的方差,σt2为接收机钟差计算结果的方差。在改进的RAIM算法中,内符合精度检验门限为不存在卫星故障时的卫星定位中误差σs。
式(4)中Qv对角线元素qvi为各伪距残差的权倒数,由于伪距观测值相互独立,可得:
| $ q_{v_{i}}=\frac{1}{P_{i}}-\boldsymbol{H}_{i}\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{H}\right)^{-1} \boldsymbol{H}_{i}^{\mathrm{T}} $ | (15) |
式中,
| $ \sigma_{v_{i}}^{2}=\sigma_{0}^{2} q_{v_{i}} $ | (16) |
标准化残差可表示为:
| $ \tilde{v}_{i}=\frac{v_{i}}{\sqrt{\sigma_{v_{i}}^{2}}} $ | (17) |
将事先给定的误警率平均分配给每颗卫星,根据标准正态分布概率表获得每个统计量的检验门限。若
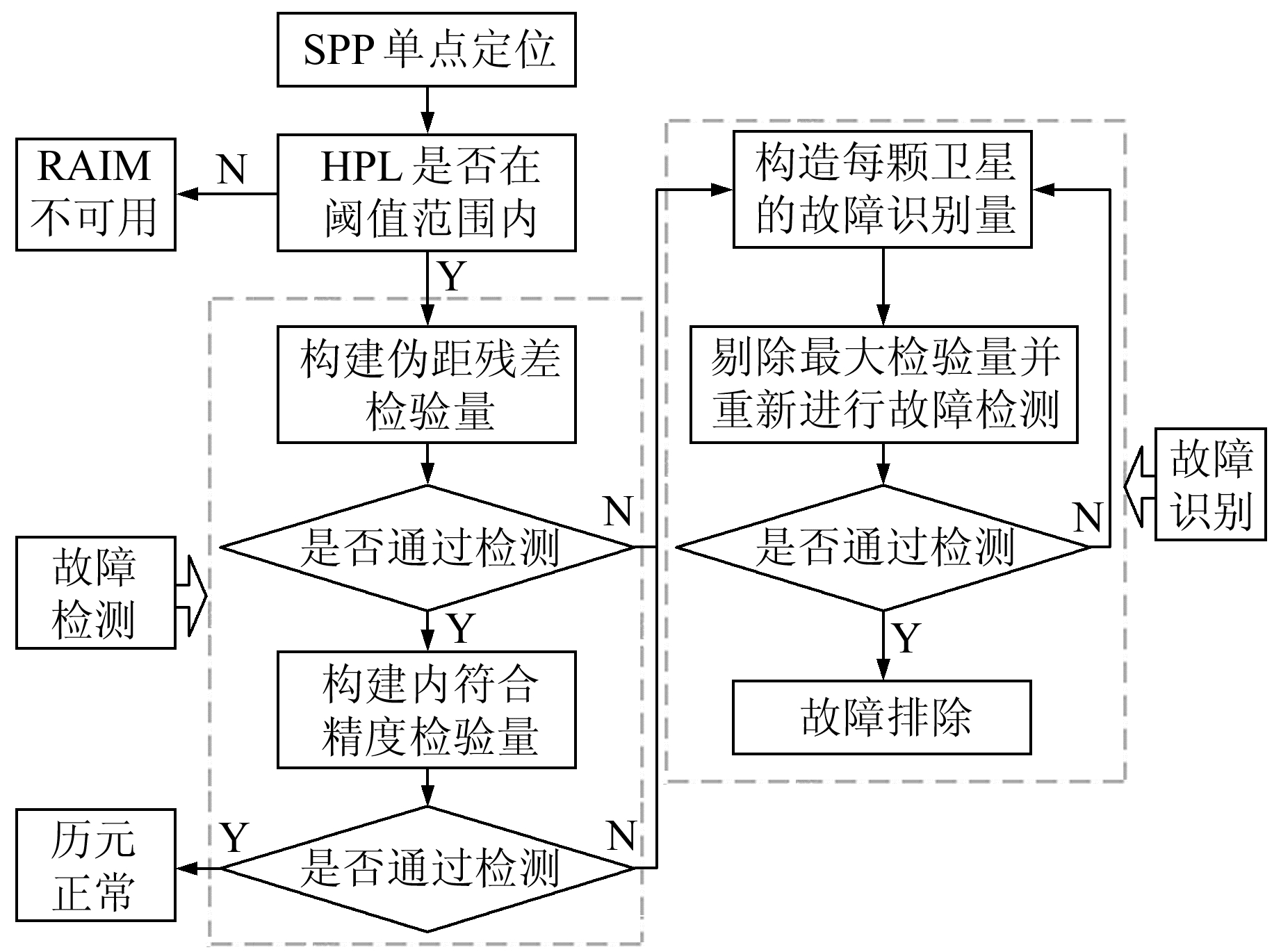
传统最小二乘残差法假设最小二乘残差中存在粗差,根据每颗卫星的检验统计量一次性排除多颗问题卫星。但最小二乘残差法存在系数矩阵病态的问题,观测量的微小波动会使得最终计算结果产生较大波动,一次性排除故障卫星可能会出现漏排、错排现象。据此,本文对故障识别流程进行改进,并不将所有超出门限的卫星都作为故障卫星进行排除,而是剔除检验量绝对值最大且超出门限的卫星,重新进行定位,再进行故障识别,直至检测不出故障卫星为止。改进的RAIM算法处理流程如图 1所示。
|
图 1 改进的RAIM算法处理流程 Fig. 1 Processing flowchart of improved RAIM algorithm |
由于低轨卫星在轨道上保持高速运动,而且GPS接收机天线受安装条件限制,以及受卫星姿态变化和空间环境影响,故其实测数据精度和理论精度差异较大[11]。实验采用2016-01-01低轨卫星GRACE-A和GRACE-B全天的观测数据,采样间隔为10 s。选取这两组数据分别进行实验,并将实验结果与简化动力学轨道进行对比分析。起算基准采用广播星历,电离层延迟采用消电离层组合模型进行改正,随机模型采用基于卫星高度角的正弦函数模型进行定权。计算过程中,因GPS卫星P码伪距观测噪声中误差约为3 m,故将σ0设置为3 m,PMD设置为0.01,PFA设置为0.001,水平告警门限HAL设置为500 m。
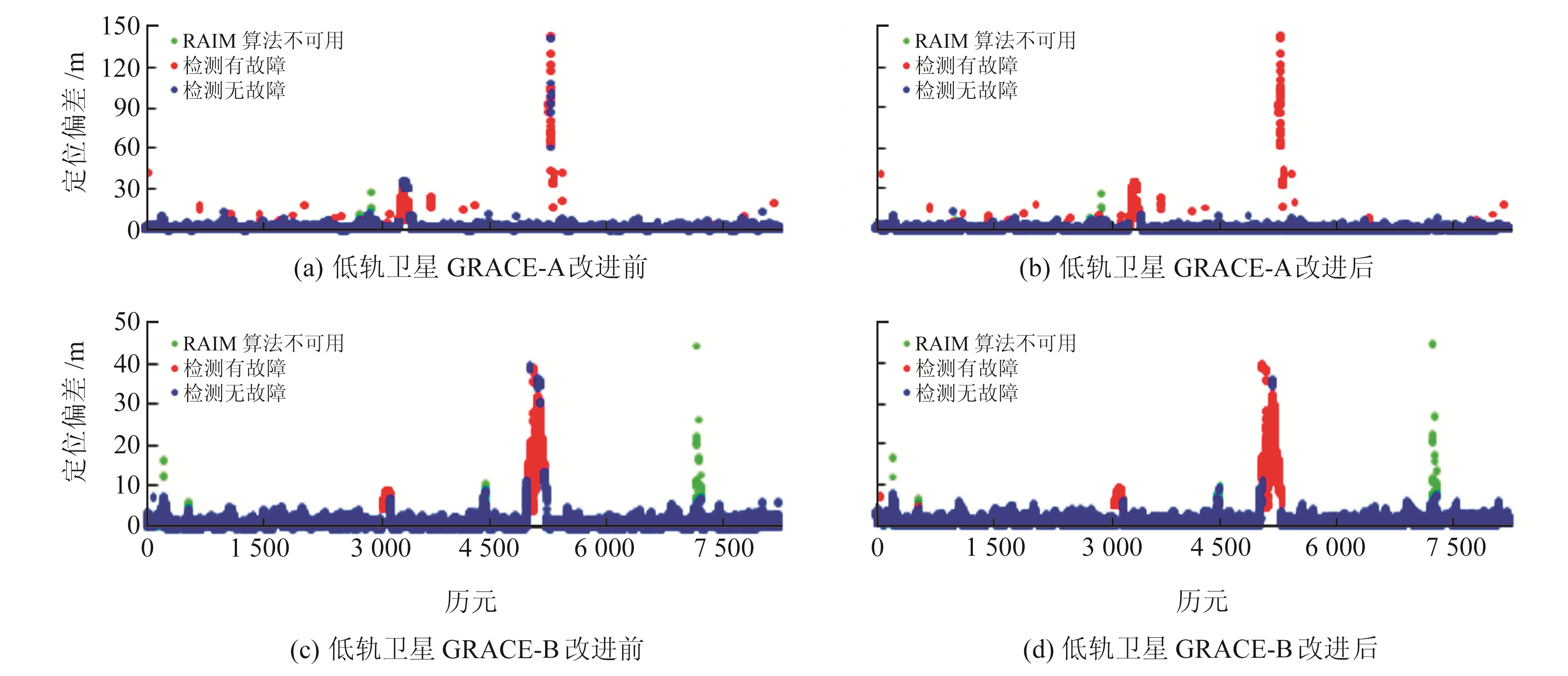
相较于地面静止测站,低轨卫星定位中误差较大,实验将内符合精度检验门限设置为8 m。图 2为两组数据分别使用传统RAIM算法和改进的算法进行故障检测的结果。
|
图 2 故障探测算法改进前后结果对比 Fig. 2 Comparison of results before and after improvement of fault detection algorithm |
由图 2可知,传统故障检测方法完全依赖于伪距残差进行卡方检验,可检测出大部分故障历元,但仍存在很多漏检的情况;改进的故障检测算法通过对卫星定位解的分布情况进行检验,对定位偏差大于40 m的历元全部发出告警信息。相较于GRACE-A卫星,GRACE-B卫星定位偏差明显更小,对于存在微小定位偏差的历元,故障检测难以成功。由于内符合精度会随着定位偏差的增大而发生跳变,因此对于存在10 m左右定位偏差的情况,改进的故障检测算法的故障检测成功率更高,漏检率更低。改进前后的漏检率和误警率数据如表 1所示。
|
|
表 1 改进前后的漏检率及误警率 Tab. 1 The missed detection rate and false alarm rate before and after improvement |
由表 1可知,改进的算法将GRACE-A数据的漏检率从4.66%降低至1.95%;GRACE-B数据质量更高,漏检率从2.21%降低至0.81%。虽然改进的故障检测算法引进更严格的检验门限可稍稍提高误警率,但提高幅度并不大。实验结果表明,改进的故障检测算法可在牺牲很小量误警率的情况下大幅降低漏检率。
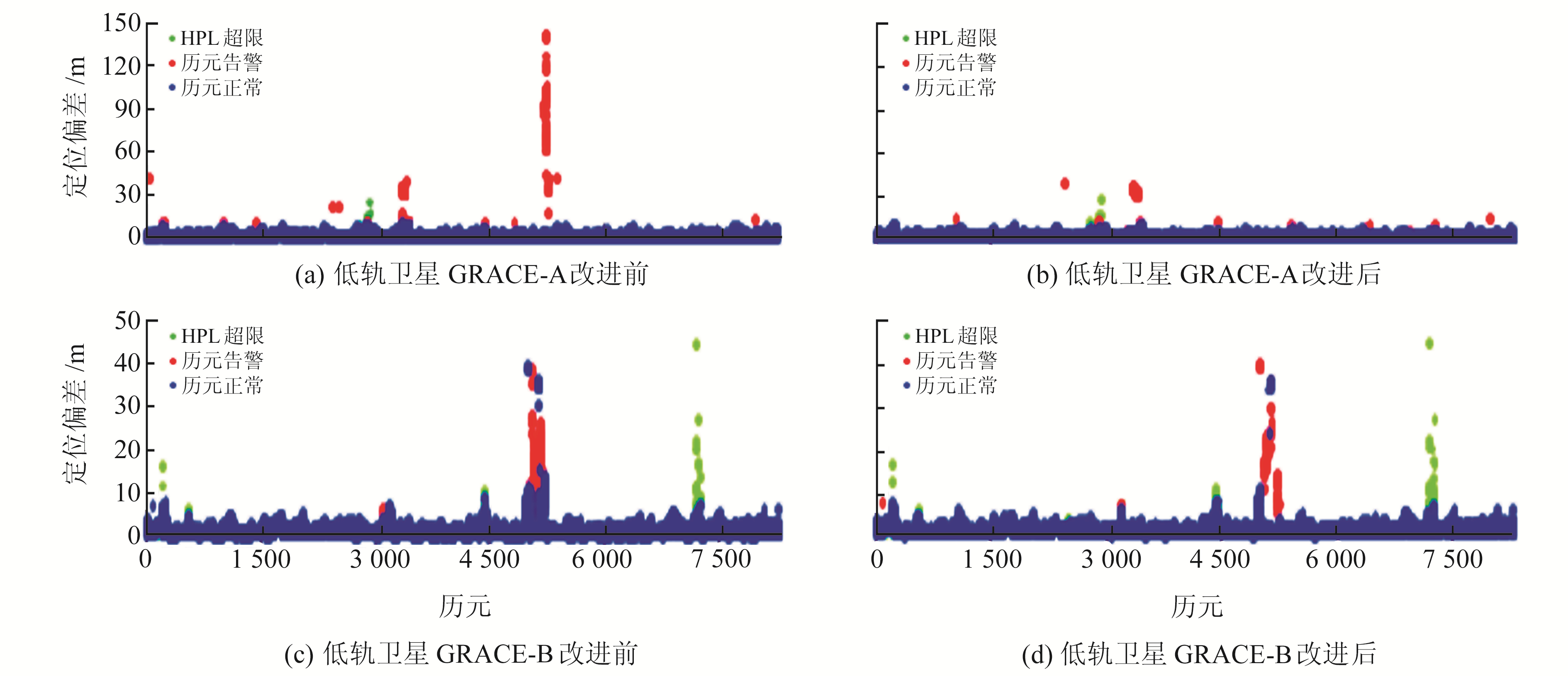
为验证本文提出的改进故障识别算法的有效性,分别采用传统故障识别算法和改进的故障识别算法对两组数据进行故障识别,图 3为两组数据的故障识别结果。
|
图 3 故障识别算法改进前后结果对比 Fig. 3 Comparison of results before and after improvement of fault identification algorithm |
对比图 3(a)和3(b)、图 3(c)和3(d)可知,当定位偏差大于40 m时,传统故障识别算法并不能有效识别和排除故障卫星。这是因为利用最小二乘法计算得到的定位结果会受到故障卫星影响而发生偏移,使得正常卫星的残差变大,传统故障识别算法会错误地认为历元存在多颗问题卫星并将其全部排除,使得历元可用卫星数不足。同时,当故障卫星导致的定位偏差较小时,最小二乘矩阵病态的问题会掩盖其他故障卫星的存在,使得传统故障识别算法难以准确识别出正确的故障卫星。相较于传统故障识别算法,改进的故障识别算法每次仅排除检验统计量最大的故障卫星,并利用其他卫星重新进行定位计算,这样可以避免定位结果受到故障卫星的影响,从而使得故障识别更加准确。
表 2、表 3分别为低轨卫星GRACE-A和GRACE-B故障识别数据统计结果。
|
|
表 2 GRACE-A故障识别数据统计 Tab. 2 Statistics of fault identification data of GRACE-A |
|
|
表 3 GRACE-B故障识别数据统计 Tab. 3 Statistics of fault identification data of GRACE-B |
由表 2、表 3可知,传统故障识别算法和改进的故障识别算法均可进行单故障及多故障卫星识别和排除。但是传统故障识别算法一次性排除所有故障卫星,未考虑到最小二乘存在矩阵病态的问题,可能会出现漏排、错排现象。改进的故障识别算法考虑到最小二乘法受异常值影响大的特点,根据伪距残差构建检验统计量逐个识别并排除故障卫星,其故障识别更加准确,可靠性更高。
4 结语针对传统RAIM算法基于最小二乘残差进行故障检测和识别,故障检测漏检率过高且故障识别存在漏排、错排现象,本文提出一种改进的RAIM算法。该算法在基于伪距残差平方和进行故障检测基础上,利用卫星定位内符合精度增设新的检验门限,可进一步降低完好性漏检率;同时,改进的算法对传统故障识别流程进行改进,每次仅排除检验统计量最大的故障卫星并重新进行定位和故障检测,直至故障全部排除,可较好地克服传统故障识别算法因未考虑到最小二乘存在矩阵病态的问题而导致故障识别不准确的缺陷。本文采用2016-01-01低轨卫星GRACE-A和GRACE-B全天的观测数据进行实验,结果表明,改进的RAIM算法可以在牺牲很小量误警率的情况下大大降低漏检率,同时可有效提高故障识别的成功率和可靠性,为接收机自主完好性监测故障检测及识别提供了一种新方法。
| [1] |
喻思琪, 张小红, 郭斐, 等. 卫星导航进近技术进展[J]. 航空学报, 2019, 40(3) (Yu Siqi, Zhang Xiaohong, Guo Fei, et al. Recent Advances in Precision Approach Based on GNSS[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(3))
(  0) 0) |
| [2] |
Lee Y C. Analysis of Range and Position Comparison Methods as a Means to Provide GPS Integrity in the User Receiver[C]. The 42nd Annual Meeting of the Institute of Navigation, Seattle, 1986
(  0) 0) |
| [3] |
Brown R G, McBurney P W. Self-Contained GPS Integrity Check Using Maximum Solution Separation[J]. Navigation, 1988, 35(1): 41-53 DOI:10.1002/j.2161-4296.1988.tb00939.x
(  0) 0) |
| [4] |
Parkinson B W, Axelrad P. Autonomous GPS Integrity Monitoring Using the Pseudorange Residual[J]. Navigation, 1988, 35(2): 255-274 DOI:10.1002/j.2161-4296.1988.tb00955.x
(  0) 0) |
| [5] |
陈柯勋, 张雪英, 邱伟. 一种改进的GNSS接收机完好性监测算法[J]. 哈尔滨理工大学学报, 2021, 26(3): 103-107 (Chen Kexun, Zhang Xueying, Qiu Wei. An Improved Integrity Monitoring Algorithm for GNSS Receiver[J]. Journal of Harbin University of Science and Technology, 2021, 26(3): 103-107)
(  0) 0) |
| [6] |
杨传森, 徐肖豪, 刘瑞华, 等. GPS RAIM定位误差保护限值算法分析[J]. 安徽大学学报: 自然科学版, 2011, 35(3): 76-81 (Yang Chuansen, Xu Xiaohao, Liu Ruihua, et al. Analysis of Algorithms for GPS RAIM Position Integrity Risk[J]. Journal of Anhui University : Natural Sciences, 2011, 35(3): 76-81)
(  0) 0) |
| [7] |
舒宝, 李一, 王利, 等. 基于卫星特征斜率加权的RAIM性能分析[C]. 第十三届中国卫星导航年会, 北京, 2022 (Shu Bao, Li Yi, Wang Li, et al. RAIM Performance Analysis Based on the Satellite Characteristic Slope Weighted[C]. The 13th China Satellite Navigation Annual Conference, Beijing, 2022)
(  0) 0) |
| [8] |
陈小平, 滕云龙. 接收机自主完好性监测算法研究[J]. 电子科技大学学报, 2008, 37(2): 218-220 (Chen Xiaoping, Teng Yunlong. Study of Receiver Autonomous Integrity Monitoring Algorithm[J]. Journal of University of Electronic Science and Technology of China, 2008, 37(2): 218-220 DOI:10.3969/j.issn.1001-0548.2008.02.016)
(  0) 0) |
| [9] |
Yang C S, Xu X H, Liu R H, et al. An Improved RAIM Algorithm Based on the Total Least Squares[C]. 2008 International Conference on Computational Intelligence and Security, Suzhou, 2008
(  0) 0) |
| [10] |
陈金平, 曹月玲, 徐君毅, 等. 卫星导航系统完好性原理与方法[M]. 北京: 国防工业出版社, 2021 (Chen Jinping, Cao Yueling, Xu Junyi, et al. Principle and Method of Navigation Satellite System Integrity[M]. Beijing: National Defense Industry Press, 2021)
(  0) 0) |
| [11] |
王甫红, 刘基余. 星载GPS伪距测量数据质量分析[J]. 测绘科学技术学报, 2007, 24(2): 97-99 (Wang Fuhong, Liu Jiyu. Data Quality Analysis of Space-Borne GPS Code Measurements[J]. Journal of Geomatics Science and Technology, 2007, 24(2): 97-99)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


