2. 上海海洋大学海洋科学学院,上海市沪城环路999号,201306
卫星测高技术自20世纪70年代起就被广泛应用于大地测量学和海洋学等学科,其主要方法是利用卫星雷达高度计回波信号,计算卫星至星下点距离,并结合卫星定轨高度,进而获得该点相对于参考椭球面的大地高。在远海开阔海域,该技术可以达到cm级精度;但在近岸海域,数据精度受陆地影响较大,导致所测数据常不被采用[1]。
随着技术的进步,为提高测高数据精度,波形重定技术应运而生。该方法大致可分为两类:一类是基于模型的波形重定,如β参数算法[2]、海洋-1(Ocean-1或MLE3)[3]、海洋-2(Ocean-2或MLE4)[3]等;另一类是基于经验的波形重定,如重心偏移(offset center of gravity, OCOG)算法[4]、Threshold法[5]、多子波参数重跟踪算法[6]等。上述方法在特定环境下可取得较好效果,但仍不能满足近岸海域的精度需求。研究发现,清除波形中包含的噪声信息,称之为“波形去污”,能够改善数据质量[7]。其中,奇异谱分析(SSA)是一种有效的时间序列分析方法,可从嘈杂数据中提取关键信息[8]。SSA首先将原始数据进行分解以获得基本信息,然后重构主要波形信息以形成新的时间序列。因此,利用SSA处理和重定波形,有望进一步提高测高数据质量。
1 数据来源本文所用数据为AVISO(archiving validation and interpretation of satellite oceanographic)官网发布的Jason-3卫星SGDR(sensor geophysical data records) F版本数据,包含20 Hz波形数据。Jason-3卫星发射于2016-01-17,作为Jason-2卫星的继任卫星,可为全球气候预测和海洋地形研究提供高精度的监测数据。然而,该卫星与其他卫星一样,其在近海的测高数据质量受海岸、海底地形等影响而变得很差。因此,针对Jason-3卫星提出新的波形重定方法,对改善近海测高数据精度具有重要意义。
到目前为止,Jason-3卫星已执行2个不同阶段的精密重复任务(exact repeat mission, ERM),其中第2阶段卫星运行轨道处于第1阶段卫星运行轨道中间位置。本文第1阶段Jason-3卫星数据称为ERM1数据, 数据时间段为2016-02-12~2022-04-07(第0~227周期);第2阶段Jason-3卫星数据称为ERM2数据,数据时间段为2022-04-25(第300周期)开始至今,目前Jason-3卫星仍在轨运行。
本文选取Jason-3卫星经过中国南海及其邻域(105°~125°E, 0°~25°N)的高度计回波波形数据,图 1为Jason-3卫星在中国南海及其邻域的地面轨迹。

|
图 1 中国南海及其邻域的Jason-3卫星地面轨迹 Fig. 1 The ground tracks of Jason-3 satellite in the south China sea and its adjacent areas |
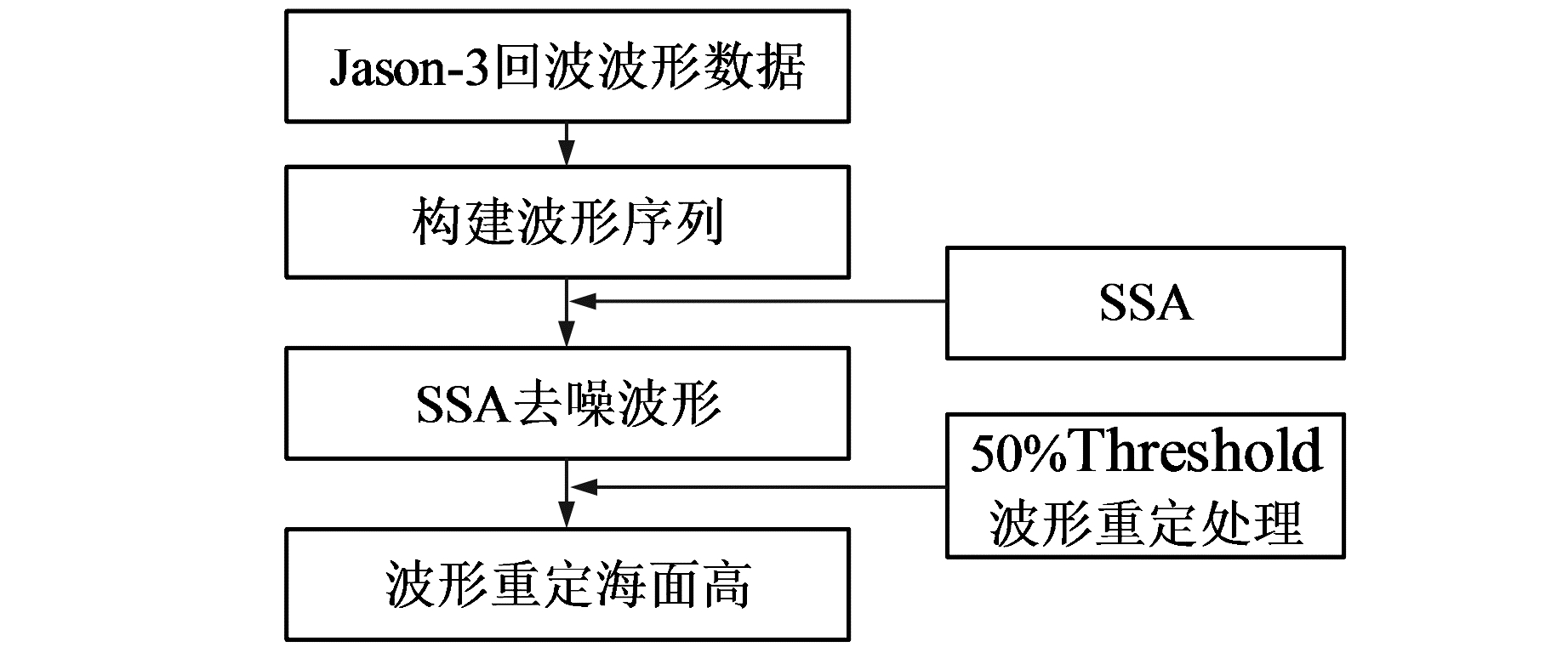
将Jason-3轨迹上的单个波形首尾相连构成波形序列,并采用SSA对波形序列进行去噪处理,以获得SSA去噪波形(简称为SSA波形)。对SSA波形采用50%Threshold波形重定方法进行波形重定处理,以得到重定海面高。图 2为处理流程。
|
图 2 Jason-3回波波形数据处理流程 Fig. 2 Processing flowchart of Jason-3 echo waveforms |
SSA通过对一维非零时间序列构造多维轨迹矩阵,并对轨迹矩阵进行分解和重构,从而提取出代表原时间序列不同成分的信号,如趋势、周期和噪声信号等[8]。
假设由i个波形构成的波形序列为X(i){xi: 1<i<N},该波形序列长度为N=104×i,104为Jason-3单个波形对应的跟踪门数。对该波形序列进行SSA分解与重构,详细过程见文献[9]。
2.2 波形重定方法波形重定是改善测高数据质量的有效手段。文献[10]对各类波形重定方法及其在近海高度计回波波形中的应用进行详细分析,且已有研究表明基于模型的波形重定方法,如β参数算法、Ocean-1、Ocean-2等,并不适用于近海复杂环境条件下的高度计回波波形重定。相比于基于模型的波形重定方法,基于经验的波形重定方法更易于实现,且已成功应用于近海测高数据质量改善方面,如OCOG和Threshold波形重定方法等。本文选取当前使用较成熟的波形重定方法,如OCOG算法、Threshold方法和5-β参数法,以验证基于SSA去噪的Jason-3波形重定方法的效果。
3 数据处理结果及分析 3.1 波形序列分析采用SSA对Jason-3卫星20 Hz波形数据进行分解重构。选取Jason-3 cycle310 pass153(19.91°~21.65°N)(简称为c310-p153轨迹)频率为20 Hz的波形数据作为处理对象,如图 1中紫色线轨迹。所选数据包含从陆地到海洋和海洋到陆地的测高数据,所经海域最深处约1 730 m,最浅处约7 m,既包含近海测高数据又包含远海测高数据,总共有3 118个波形,数据量充足,具有一定的代表性。将这些波形连接在一起构成波形序列(简称为c310-p153波形序列),波形序列长度为3 118×104,采用SSA对该波形序列进行分解重构,分离出噪声信息,从而得到新的波形序列,新波形序列已剔除噪声信息,称之为SSA波形序列。
采用SSA对波形序列进行分解和重构之前,需要确定两个重要参数,为窗口长度M和波形主成分的个数l,即确定子集D1={1, …, l}大小。M太大会使奇异值分解得到的不同重构成分产生混叠,M太小会造成波形中包含的主要波形信息与噪声信息无法很好地分离。前l个成分能够很好地表达波形中所包含的主要信息,而后M-l个成分表达的是波形中包含的噪声信息。l太小会使波形中主要信息包含噪声信息,l太大会造成波形过度分解,可能导致将波形中部分主要信息误认为噪声信息。对于这两个参数的确定,目前未有较为明确的标准。文献[11]对窗口长度进行分析,认为窗口长度选取为104可较好地分离出波形序列中的主要波形信息成分和噪声信息成分。因此,本文选取窗口长度M为104。l值大小可根据各成分占原始波形序列能量的比值来确定,称之为贡献率。
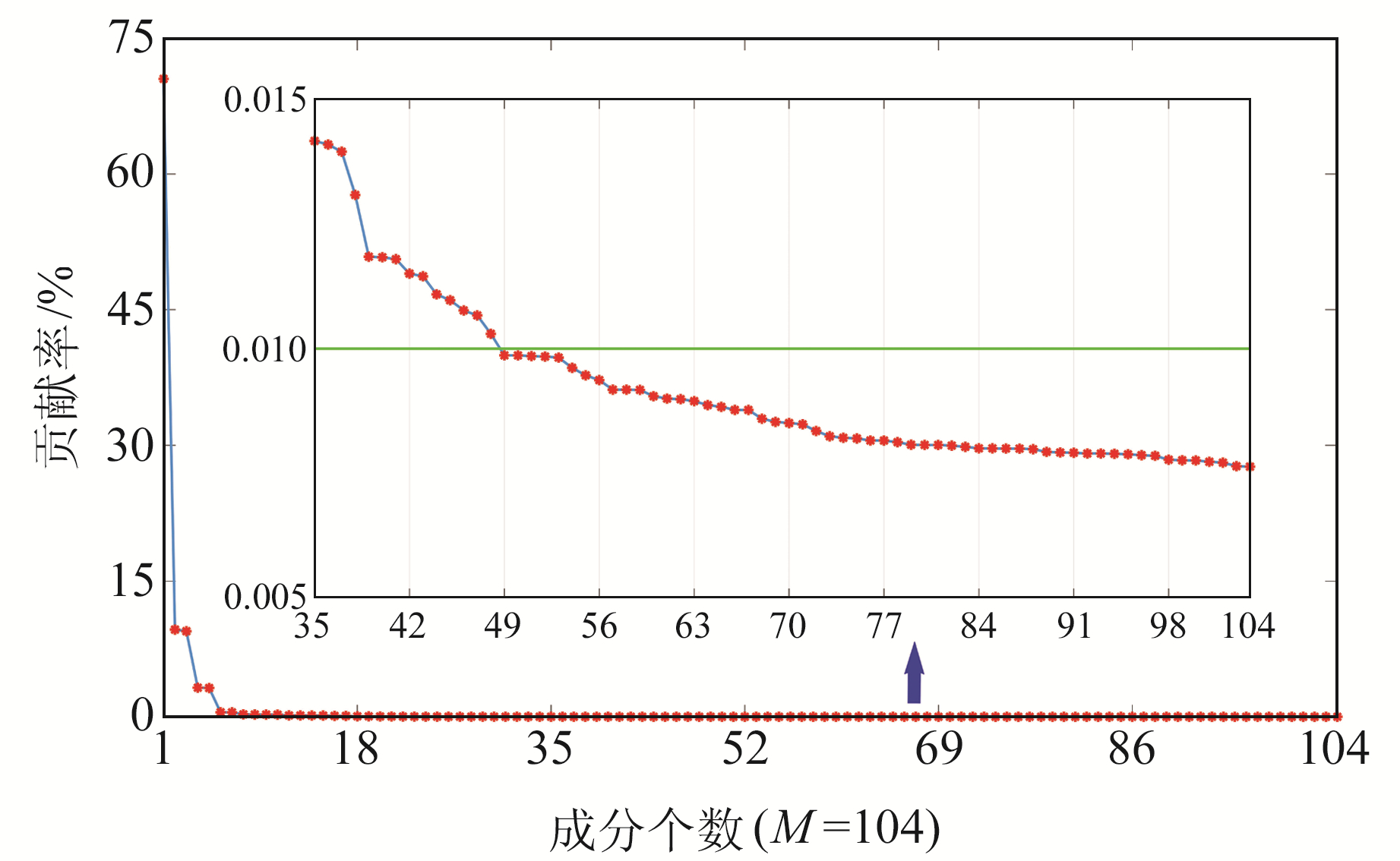
图 3为各成分的贡献率情况,从图中可以看出,除第1个成分的贡献率达到约71.4%外,其他成分的贡献率均低于10%。从第49个成分开始,各成分的贡献率均低于0.01%。为保证重构后的波形序列能够很好地保留原始波形的重要信息,即波形前缘振幅、斜率信息保持不变,并尽可能地剔除波形序列中所包含的噪声信息,本文取贡献率经验值0.01%为标准,在所有成分中,将贡献率低于0.01%的成分归位于噪声信息,贡献率高于0.01%的成分归位于主要波形信息。因此,对于c310-p153波形序列,经过SSA分解,取前48个成分进行重构得到代表主要信息的波形序列(称之为SSA波形序列),后56个成分进行重构得到噪声信息残差序列。前48个成分总贡献率为99.43%,后56个成分总贡献率仅为0.57%,因此,重构后的SSA波形序列可以很好地保持原始波形序列的主要信息成分。
|
图 3 特征值对应成分的贡献率 Fig. 3 The contribution ratio of components corresponding to eigenvalues |
图 4为c310-p153轨迹上经过SSA分解重构的前50个波形构成的波形序列及其残差序列。从图 4(a)可以看出,原始波形与SSA波形的主要差异体现在波形热噪声区和波形幅值上,而波形的前缘信息得到很好的保留,这表明SSA可以有效实现Jason-3波形消噪处理。从图 4(b)可以看出,残差序列振幅较大的区域主要集中在前后波形的交界处,其主要原因为波形后缘容易受到后面波形热噪声区低频信号的影响,而波形前缘部分所受影响较小。

|
图 4 原始波形序列和SSA波形序列的前50个波形以及相对应的残差序列 Fig. 4 The first 50 waveforms of raw waveform series and SSA waveform series and corresponding residual series |
对c310-p153轨迹上SSA分解重构前后的波形分别采用OCOG、阀值为50%的Threshold(简称50%Threshold)和5-β等3种波形重定方法进行波形重定处理,并将重定结果与EGM2008确定的大地水准面高进行比较,通过计算波形重定改善率[12](improvement percentage, IMP)判断重定结果的质量。
图 5为重定海面高比较结果,其中Ocean波形重定算法得到的海面高由Jason-3 SGDR数据提供,Raw为原始波形不经过波形重定处理计算得到的海面高。从图中可以看出,沿纬度方向,经过波形重定处理得到的海面高要比原始波形未经过波形重定处理得到的海面高更平滑,并且重定后的海面高与EGM2008模型计算得到的大地水准面高更相似。从图 5(a)~(c)可以看出,3种方法对SSA波形重定的海面高比对原始波形重定的海面高更平滑。除OCOG重定结果较差外,50%Threshold、5-β两种波形重定方法对SSA波形重定的海面高相较于对原始波形重定的海面高与Ocean重定结果更相似,并且重定结果在深海区域相差不大,其差异主要表现在近海区域。

|
图 5 沿c310-p153轨迹不同重定方法得到的重定海面高比较 Fig. 5 Comparison of retracked sea surface height(SSH) calculated by different methods along the c310-p153 track |
表 1为OCOG、50%Threshold和5-β三种重定算法分别对c310-p153轨迹上原始波形和SSA波形的重定结果比较。从表中可以看出,除5-β重定算法对原始波形和SSA波形的重定成功率分别为99.90%和99.84%外,其他算法对原始波形和SSA波形的重定成功率均为100%。不同重定方法对原始波形和SSA波形进行重定计算得到的IMP值不同,3种重定方法对SSA波形的重定结果均比对原始波形的重定结果好,其中OCOG算法对原始波形的重定结果最差,50%Threshold算法对SSA波形的重定结果最好,这说明对原始波形进行SSA分解重构处理能有效提高波形重定精度。
|
|
表 1 c310-p153轨迹上原始波形和SSA波形的不同重定方法重定改善率比较 Tab. 1 Comparison of improvement percentage(IMP) between different retracking methods for the raw waveforms and SSA waveforms of the c310-p153 track |
为更进一步验证SSA波形重定结果比原始波形重定结果效果好,本文在中国南海区域选取2个验潮站,分别为Quarry Bay(22.3°N, 114.2°E)和Subic Bay(14.765°N, 120.252°E),具体位置如图 1所示。离验潮站Quarry Bay最近的轨迹为Jason-3 ERM1 pass153,最近距离约为9.18 km;离验潮站Subic Bay最近的轨迹为Jason-3 ERM2 pass088,最近距离约为20.58 km。利用OCOG、50%Threshold和5-β方法分别对这2个轨迹上不同观测时间的原始波形和SSA波形进行波形重定处理,得到相应的校正海面高。
本文对验潮站水位和卫星测高的海面高数据分别计算一个随时间变化的海面波动序列,比较两者的相关性(cor)和标准差(std),结果如表 2所示。验潮站处的测高海面高序列是以验潮站为中心、30 km为半径、按反距离加权方法计算得到。
|
|
表 2 不同重定方法对原始波形和SSA波形重定得到的海面高序列与验潮站海面高序列的相关性和标准差 Tab. 2 The correlation and standard deviation between the SSH series obtained from the raw waveforms and SSA waveforms by different retracking methods and the SSH series obtained from the tide gauge |
从表 2可以看出,采用OCOG分别对原始波形和SSA波形重定的海面高与验潮站数据相比,前者的标准差和相关性大于后者,这是因为SSA对原始波形进行滤噪处理后,SSA波形相对原始波形在热噪声区出现较大的震荡,导致OCOG算法对SSA波形重定结果变差。而采用50%Threshold和5-β方法分别对原始波形和SSA波形重定的海面高与验潮站数据相比,其结果均是后者大于前者,这说明经过SSA滤噪处理能够有效提高波形重定质量。其中,50%Threshold对SSA波形重定结果与验潮站数据最接近。
4 结语本文提出采用SSA对Jason-3高度计回波波形数据进行分解重构,剔除波形中包含的噪声信息,从而提取出主要波形信息,然后进行波形重定处理,以进一步提高波形重定数据质量,达到尽可能最大化改善近海测高数据质量的目的。通过OCOG、50%Threshold和5-β三种波形重定算法对Jason-3高度计cycle310 pass153轨迹上原始波形和SSA波形分别进行波形重定处理,将重定海面高与EGM2008模型提取的大地水准面高进行对比,并比较波形重定改善率,其结果均表明测高轨迹上原始波形经过SSA滤噪处理后能有效改善波形重定数据质量,从而提高近海测高数据质量。通过对Jason-3 ERM1 pass153和ERM2 pass088轨迹上原始波形和SSA波形进行波形重定处理,将重定海面高与验潮站数据进行比较,其结果进一步表明采用SSA对原始波形进行滤噪处理后,近海测高数据质量可得到进一步改善。本文研究结果对于改善近海测高数据质量,拓宽卫星测高技术在近海的应用范围具有重要意义。
| [1] |
范雕, 李姗姗, 孟书宇, 等. Jason-2卫星波形重跟踪算法比较[J]. 海洋测绘, 2017, 37(6): 5-8 (Fan Diao, Li Shanshan, Meng Shuyu, et al. Altimetry Waveform Retracking Algorithm Comparing for Jason-2[J]. Hydrographic Surveying and Charting, 2017, 37(6): 5-8)
(  0) 0) |
| [2] |
Martin T V, Zwally H J, Brenner A C, et al. Analysis and Retracking of Continental Ice Sheet Radar Altimeter Waveforms[J]. Journal of Geophysical Research: Oceans, 1983, 88(C3): 1 608-1 616 DOI:10.1029/JC088iC03p01608
(  0) 0) |
| [3] |
Thibaut P, Poisson J C, Bronner E, et al. Relative Performance of the MLE3 and MLE4 Retracking Algorithms on Jason-2 Altimeter Waveforms[J]. Marine Geodesy, 2010, 33(S1): 317-335
(  0) 0) |
| [4] |
鄂栋臣, 杨元德. 卫星测高波形重跟踪算法在南极应用的比较[J]. 大地测量与地球动力学, 2007, 27(1): 45-49 (E Dongchen, Yang Yuande. Comparison among Several Altimetry Waveform Retracking Algorithms Applied in Antarctic[J]. Journal of Geodesy and Geodynamics, 2007, 27(1): 45-49)
(  0) 0) |
| [5] |
Davis C H. Growth of the Greenland Ice Sheet: A Performance Assessment of Altimeter Retracking Algorithms[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(5): 1 108-1 116 DOI:10.1109/36.469474
(  0) 0) |
| [6] |
焦明连, 孙佳龙. 基于聚类分析的多子波优化重定算法[J]. 海洋测绘, 2013, 33(6): 36-38 (Jiao Minglian, Sun Jialong. A Multi-Wave Optimized Retracking Method Based on Cluster Analysis[J]. Hydrographic Surveying and Charting, 2013, 33(6): 36-38)
(  0) 0) |
| [7] |
汪海洪, 罗北, 梁月, 等. 卫星雷达测高波形修正方法研究[J]. 大地测量与地球动力学, 2016, 36(3): 202-205 (Wang Haihong, Luo Bei, Liang Yue, et al. Improved Method for Modification of Satellite Radar Altimeter Waveform[J]. Journal of Geodesy and Geodynamics, 2016, 36(3): 202-205)
(  0) 0) |
| [8] |
Shen Y, Guo J Y, Liu X, et al. Long-Term Prediction of Polar Motion Using a Combined SSA and ARMA Model[J]. Journal of Geodesy, 2018, 92(3): 333-343
(  0) 0) |
| [9] |
Yuan J J, Guo J Y, Niu Y P, et al. Denoising Effect of Jason-1 Altimeter Waveforms with Singular Spectrum Analysis: A Case Study of Modelling Mean Sea Surface Height over South China Sea[J]. Journal of Marine Science and Engineering, 2020, 8(6)
(  0) 0) |
| [10] |
Gommenginger C, Thibaut P, Fenoglio-Marc L, et al. Retracking Altimeter Waveforms near the Coasts[M]//Vignudelli S, Kostianoy A, Cipollini P, et al. Coastal Altimetry. Berlin, Heidelberg: Springer, 2011
(  0) 0) |
| [11] |
Guo J Y, Di W Q, Yuan J J, et al. Satellite Radar Altimetric Waveform Simulation and Retracking over Coastal Sea Based on Singular Spectrum Analysis[C]. International Workshop on Earth Observation and Remote Sensing Applications(EORSA), Xi'an, 2018
(  0) 0) |
| [12] |
Hwang C, Guo J Y, Deng X L, et al. Coastal Gravity Anomalies from Retracked Geosat/GM Altimetry: Improvement, Limitation and the Role of Airborne Gravity Data[J]. Journal of Geodesy, 2006, 80(4): 204-216
(  0) 0) |
2. College of Marine Sciences, Shanghai Ocean University, 999 Huchenghuan Road, Shanghai 201306, China
 2023, Vol. 43
2023, Vol. 43

