2. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077;
3. 武汉大学测绘学院,武汉市珞喻路129号,430079;
4. 湖北珞珈实验室,武汉市珞喻路129号,430079;
5. 中国科学院大学地球与行星科学学院,北京市玉泉路19号甲,100049
低轨卫星精密轨道数据是解算时变重力场位系数的主要输入量之一,也是反演时变重力场模型的基础[1]。Yunck等[2]针对遥感卫星定轨分别对动力学法、简化动力学法、运动学法和局部重力调整4种定轨策略进行测试,其定轨精度优于10 cm,并详细分析各定轨策略的优缺点。Bock等[3]采用简化动力学法和非差运动学法对GRACE双星进行定轨,均能满足2 cm的定轨径向精度要求。Zehentner[4]提出非差非组合运动学法,可有效解决线性组合会放大观测噪声的问题,结果表明,GRACE-FO卫星固定解轨道精度可达1~2 cm。李建成等[5]采用大型方程快速求解算法对GRACE进行非差运动学定轨,径向精度能达到3~5 cm。
动力学法和简化动力学法定轨难以精化非保守力模型,对轨道精度有所制约。相比之下,运动学法定轨相对简单且不需要力学模型,定轨精度只受观测值精度和观测时GPS卫星几何结构影响[6]。高性能星载GPS接收机的出现使得运动学法也能取得与简化动力学法相当的定轨精度,同时由于不含重力场先验信息,运动学轨道也能提高时变重力场解算精度[7]。目前相关机构的运动学轨道数据发布存在滞后性,时延高达1 a,这会限制相关时变重力场反演的研究。因此,开展低轨卫星运动学精密定轨研究,有助于恢复地球重力场。
本文引入平滑卡尔曼滤波,利用自主研发的精密定轨软件对GRACE-FO双星进行定轨与分析。为客观评估平滑滤波定轨精度,对外符合和内符合精度进行评定,探讨平滑滤波与传统单向卡尔曼滤波相比,能否降低纯运动学定轨法对星载GPS观测值质量的过分依赖和提高轨道结果的可靠性。
1 非差运动学定轨原理与方法 1.1 观测方程低轨卫星与GPS卫星间的载波相位观测方程为:
| $ \begin{gathered} L_{\mathrm{r}, i}^{\mathrm{s}}(t)=\rho_{\mathrm{r}}^{\mathrm{s}}(t)+c \delta_{\mathrm{r}}(t)-c \delta^{\mathrm{s}}(t)+\lambda_{i} N_{\mathrm{r}, i}^{\mathrm{s}}- \\ \Delta_{\text {ion }, i}+\Delta_{\mathrm{rel}}+\Delta_{\mathrm{PCO}}^{\mathrm{GPS}}+\Delta_{\mathrm{PCO}}^{\mathrm{LEO}}+\varepsilon_{i} \end{gathered} $ | (1) |
式中,r代表低轨卫星,s代表GPS卫星,i为观测频率,Lr, is为低轨卫星r和GPS卫星s在频率i上的载波相位观测值,ρrs为低轨卫星r和GPS卫星s之间的几何距离,c为真空中光速,δr为低轨卫星r的接收机钟差,δs为GPS卫星s的卫星钟差,Δion, i为频率i上的电离层延迟改正,λi为载波波长(L1或L2),Nr, is为频率i上的载波相位整周模糊度,εi为频率i上的载波相位观测值噪声。与地面定位观测方程相比,上述观测方程不含对流层延迟改正,而多路径效应也因低轨卫星天线配置扼流圈和对卫星高度角进行限制而忽略不计[8]。
为消除一阶电离层的影响,可以利用载波相位观测值Lr, 1s和Lr, 2s形成无电离层组合,即
| $ L_{\mathrm{r}, 3}^{\mathrm{s}}=\frac{f_{2}^{2}}{f_{1}^{2}-f_{2}^{2}} L_{\mathrm{r}, 1}^{\mathrm{s}}-\frac{f_{2}^{2}}{f_{1}^{2}-f_{2}^{2}} L_{\mathrm{r}, 2}^{\mathrm{s}} $ | (2) |
式中,f1、f2分别为载波L1、L2的频率,其他参数意义与式(1)相同。
1.2 星载GPS定轨误差源及改正措施上述误差源中,卫星星历与钟差由外部文件给出[9],地球自转效应、星基和接收机端相对论效应、天线相位中心改正与天线相位缠绕由数学模型进行精确改正[10-13],大气延迟可通过线性组合方式消除其影响[14]。
1.3 随机模型不同的加权方法反映观测值之间相对精度的不同,本文采用高度角定权方法[15],其表达式为:
| $ \begin{gathered} P(E)= \\ a^{2}+\frac{b^{2}}{\sin (E)^{2}}+\sigma_{\text {eph }}^{2}+\sigma_{\text {code }}^{2}+\sigma_{\text {phase }}^{2} \end{gathered} $ | (3) |
式中,P为观测值权重,E为卫星高度角,σeph为卫星轨道和钟差中误差,σcode为伪距观测误差中误差,σphase为相位观测误差中误差,a、b为固定值。
2 基于平滑卡尔曼滤波的运动学定轨本文根据序贯最小二乘思想,设计并实现平滑卡尔曼滤波定轨。观测方程线性化可表示为:
| $ \boldsymbol{L}_{k}=\boldsymbol{H}_{k} \boldsymbol{X}_{k}+\boldsymbol{v}_{k}, \boldsymbol{v}_{k} \sim \boldsymbol{N}\left(0, \boldsymbol{R}_{k}\right) $ | (4) |
式中,Lk为观测矢量;k为时间引数;H为观测方程系数阵;Xk为状态矢量,包含坐标、钟差和模糊度参数;vk和Rk为观测噪声及其方差-协方差阵。
单向滤波中状态预测与更新如图 1所示。

|
图 1 扩展卡尔曼滤波过程 Fig. 1 Extended Kalman filtering process |
图 1中
在完成前向和后向滤波后,根据坐标协方差信息进行平滑滤波。平滑算法为:
| $ \boldsymbol{Q}_{s}=\left(\boldsymbol{Q}_{F}^{-1}+\boldsymbol{Q}_{B}^{-1}\right)^{-1} $ | (5) |
| $ \boldsymbol{X}_{s}=\boldsymbol{Q}_{s}\left(\boldsymbol{Q}_{F}^{-1} \boldsymbol{X}_{F}+\boldsymbol{Q}_{B}^{-1} \boldsymbol{X}_{B}\right)^{-1} $ | (6) |
式中,QF为前向滤波结果位置协方差信息,QB为后向滤波结果位置协方差信息,XF为前向位置信息,XB为后向位置信息,XS为平滑后的轨道结果[16]。
3 载波相位定轨精度分析本文利用自主研发的精密定轨软件处理GRACE-FO C和D卫星2020-01-01~07星载GPS观测数据,并将运动学轨道计算结果与JPL提供的科学轨道进行对比分析。2020-01-01 GRACE-FO C星两种滤波方法轨道计算结果与科学轨道对比如图 2所示,由图可知,C星平滑滤波定轨结果在X、Y、Z三个方向的差异基本都小于5 cm,均不存在显著的系统误差,能够获得稳定的高精度轨道结果。

|
图 2 C星doy1两种滤波方法轨道残差对比 Fig. 2 Comparison of track residuals of two filtering methods for satellite C on doy1 |
由图 3(b)可知,D星前向滤波结果中存在大量轨道异常值,最大值达70 m。经检核发现,由于观测数据质量问题,滤波迭代时验前和验后残差数据处理过程中剔除了过多卫星,该历元GPS卫星接收数仅为4,导致方程对未知参数的约束减弱。对比图 3(a)发现,平滑滤波对该现象具有很好的平滑效果,最终仍能取得高精度的运动学轨道。

|
图 3 D星doy1两种滤波方法轨道残差对比 Fig. 3 Comparison of track residuals of two filtering methods for satellite D on doy1 |
综合图 2和图 3,分析比较2020-01-01平滑滤波和前向滤波计算的3个方向轨道结果和协方差可知,平滑算法对滤波前期收敛慢导致的轨道异常值具有很好的平滑效果,能够显著提高开始阶段的定轨精度。但由于前向和后向滤波最后阶段参数的协方差在数值和阶次上一致,该算法对最后阶段滤波发散的改善效果较小。
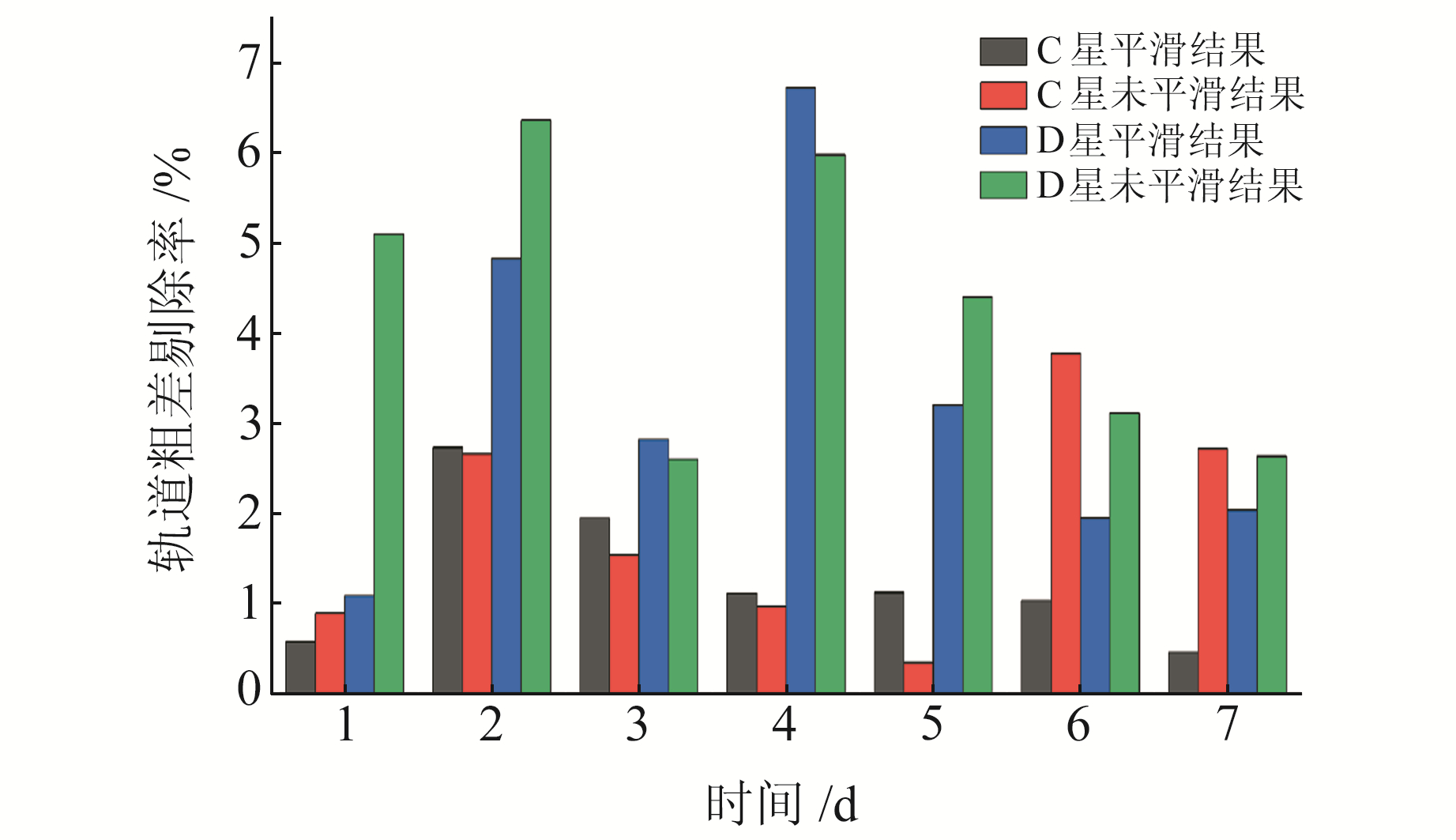
在每日观测数据的结尾部分,由于对卡尔曼滤波参数调节的不完善,导致滤波最后阶段发散,本文对10 s采样率的运动学轨道结果进行残差编辑,剔除观测卫星数小于4和滤波发散的历元。图 4为GRACE-FO双星在两种滤波方法下的7 d定轨结果剔除率,对比可知,多数情况下平滑滤波相较于单向滤波能够极大地降低定轨结果的剔除率,整体提高定轨精度,保证轨道结果的有效性。在少数情况下,由于观测数据质量问题或周跳探测不完全等,两种滤波方法的剔除率相当。
|
图 4 运动学轨道粗差剔除率比较 Fig. 4 Comparison of gross error elimination rate of kinematic orbit |
图 5、6为GRACE-FO C和D星2020-01-01~07前向滤波和平滑滤波定轨结果与JPL轨道结果的残差在X、Y、Z三个方向的均方根误差分布。结合图 2和图 5可知,doy1 C星观测数据质量较好,不存在数值较大的轨道异常值,因此3个方向的前向滤波轨道残差RMS值均小于10 cm。此外,双星前向滤波轨道残差RMS值均处于dm级,少数日期轨道异常值较大,RMS值可达m级。

|
图 5 doy1~7前向滤波轨道残差RMS值 Fig. 5 Track residual RMS values of forward filtering on doy1-7 |
|
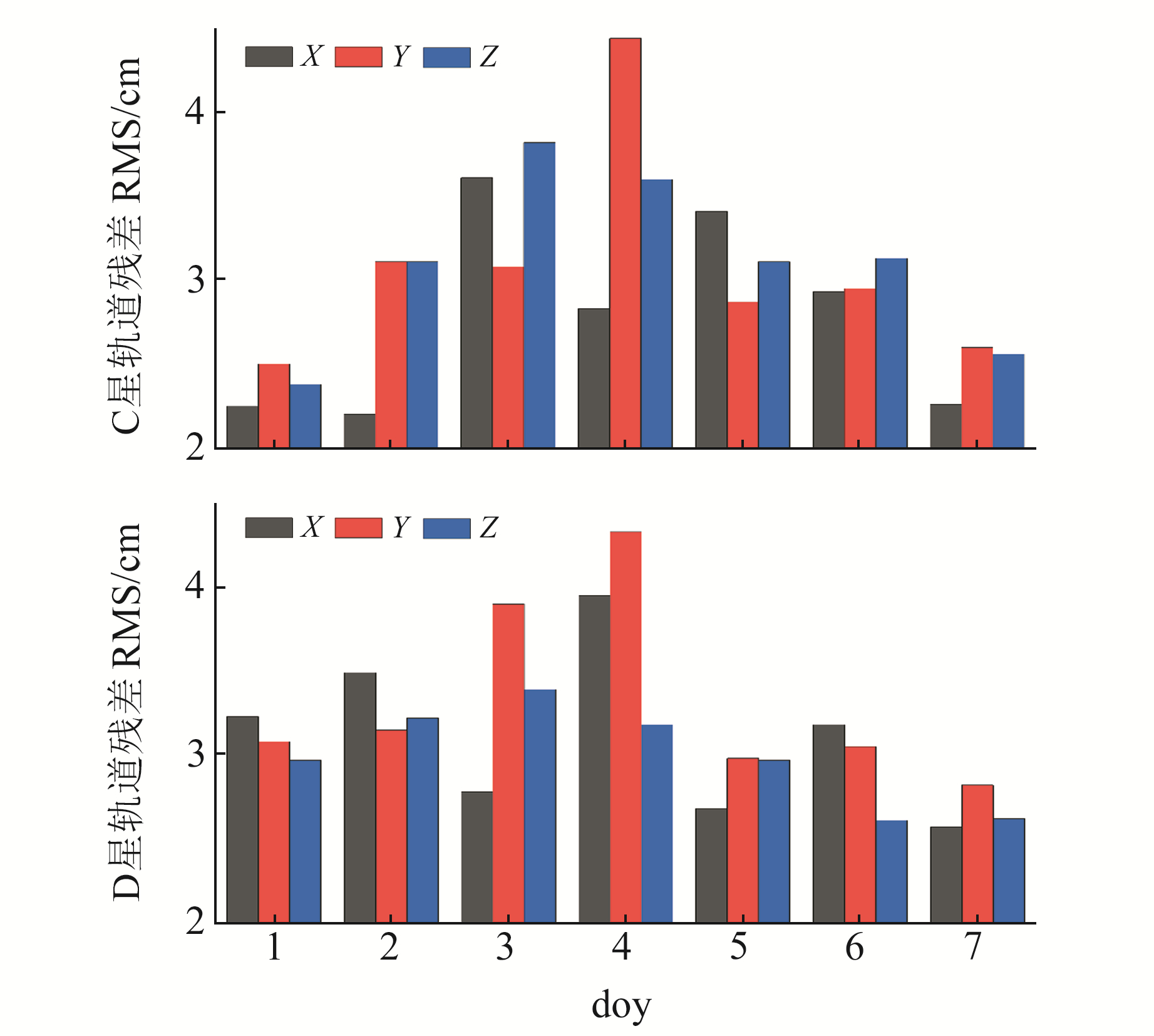
图 6 doy1~7平滑滤波轨道残差RMS值 Fig. 6 Track residual RMS values of smooth filtering on doy1-7 |
由图 6可知,GRACE-FO C和D星平滑滤波轨道X方向精度分别为2~3 cm和3~4 cm,其中最大值分别为3.41 cm和3.95 cm,7 d轨道三维坐标精度分别为5.20 cm和5.47 cm。可以看出,C星定轨精度比D星高,由GRACE-FO官方给出的轨道故障和机动文件(ftp://isdcftp.gfz-potsdam.de/grace-fo/DOCUMENTS/TECHNICAL_NOTES/TN-01a_SCE.txt) 可知,该阶段D星作为跟踪卫星,需要不断在高速状态下调整姿态和轨道以保证KBR测距系统正常工作,力学模型较为复杂,轨道精度会受到一定影响。综合分析两种滤波轨道残差RMS可知,平滑滤波相较于传统的单向滤波能够有效提升整体定轨精度。
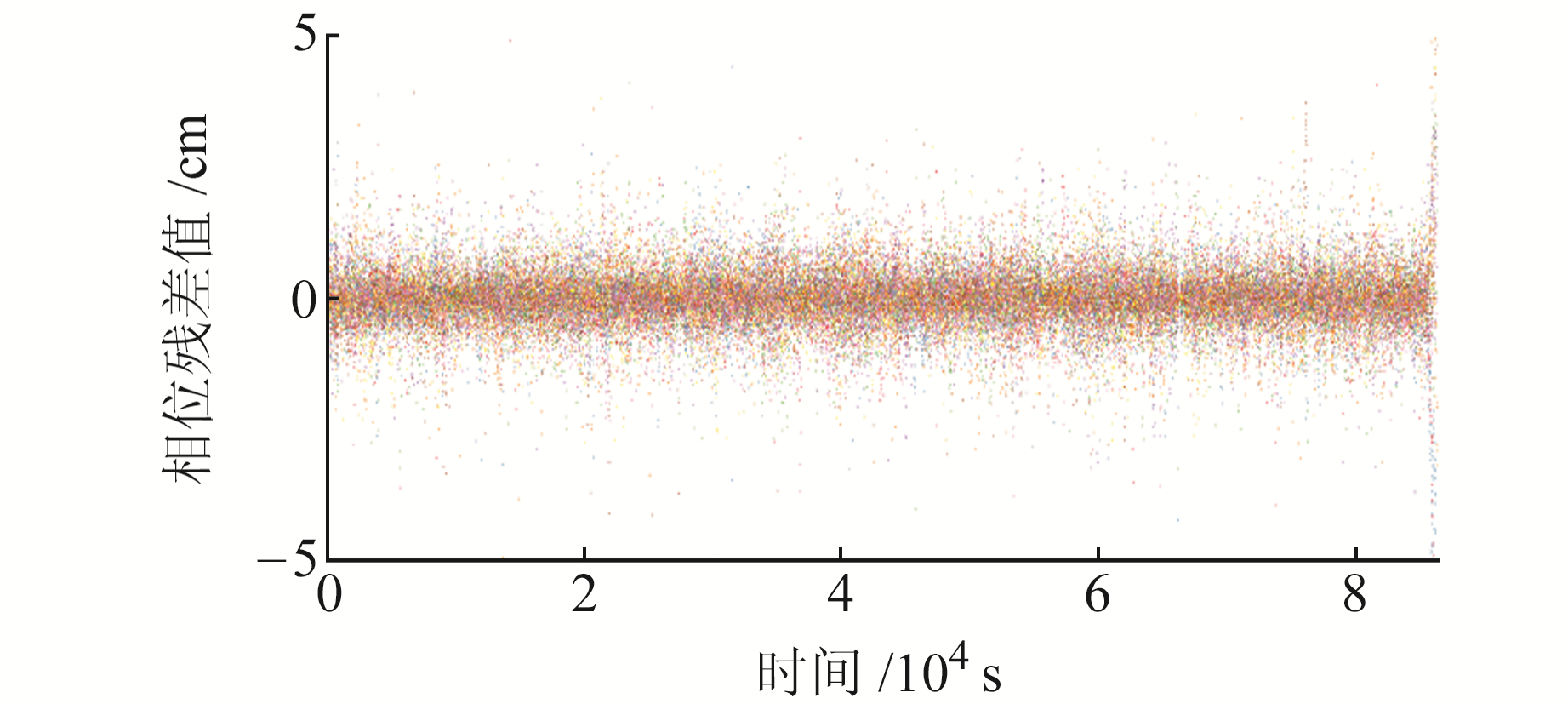
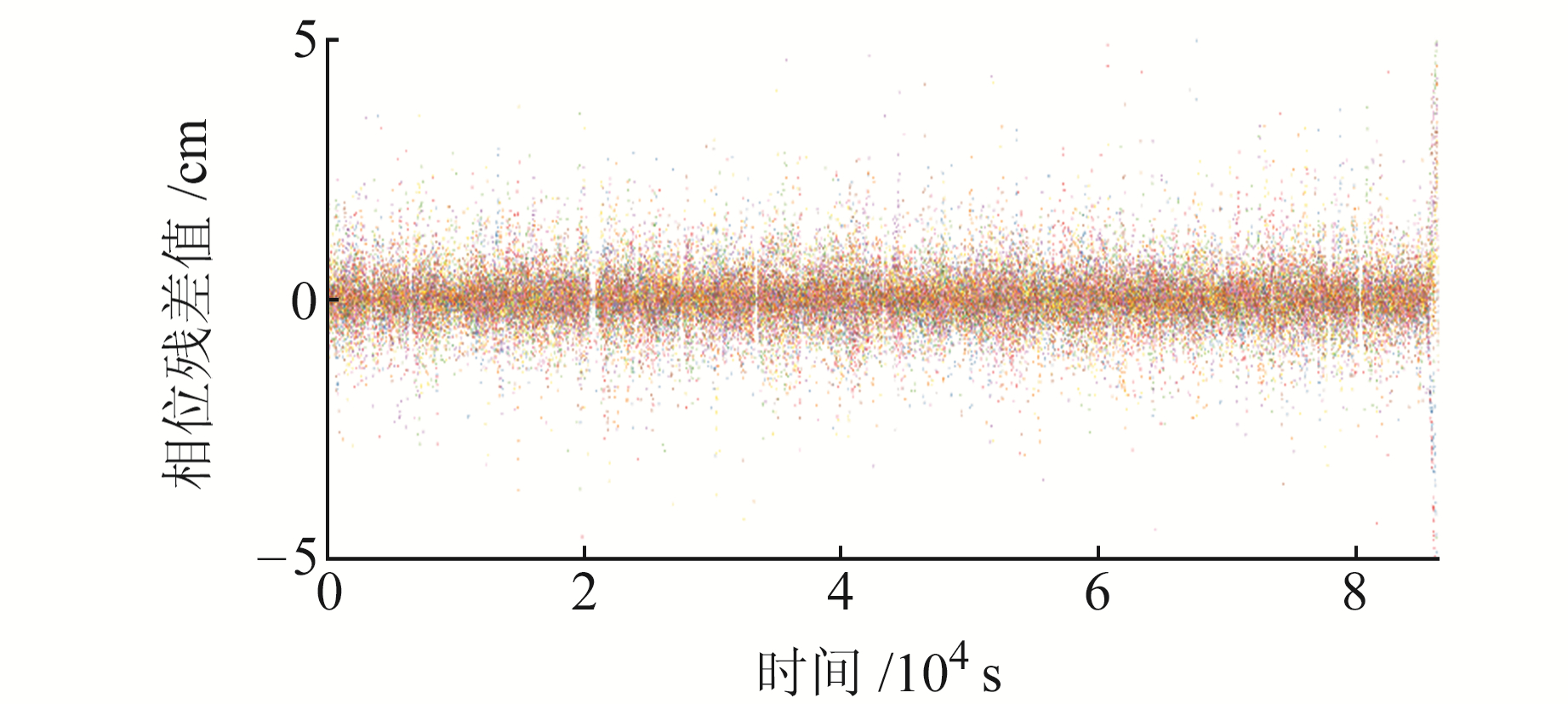
本文在进行运动学轨道外符合精度评定的同时进行残差分析。图 7、8为2020-01-01 GRACE-FO C和D卫星相位无电离层组合残差,可以看出,除数据结尾部分由于滤波发散导致残差分布在±10 cm之间,其余残差值均分布在±5 cm以内,残差均值为0。上述分析表明,本文采用的MW(Melbourne-Wubbena)和GF(Geometry-Free)组合周跳探测算法及残差编辑算法具有可行性。
|
图 7 C星相位无电离层组合残差 Fig. 7 Phase ionosphere-free combination residual of satellite C |
|
图 8 D星相位无电离层组合残差 Fig. 8 Phase ionosphere-free combination residual of satellite D |
基于低轨卫星精密定轨原理,本文在扩展卡尔曼滤波基础上增加平滑算法,利用自主研发的精密定轨软件处理2020-01星载GPS观测数据,并对GRACE-FO进行非差运动学定轨,得到以下结论:
1) 采用本文方法计算的GRACE-FO卫星3个坐标分量的定轨精度分别为2~3 cm、2~4 cm和3~4 cm。
2) 本文采用的平滑滤波算法相较于单向滤波可明显改善由于滤波器前期预热导致的轨道异常问题,提高定轨开始阶段的定轨精度。在星载GPS观测值质量不高的情况下,平滑滤波能很好地解决由于剔除卫星阈值设置、观测GPS卫星数不够带来的轨道异常值较大的问题,降低运动学轨道结果的剔除率,提高轨道结果的可靠性,也可间接降低纯运动学法定轨对星载GPS观测值质量的依赖,整体提高定轨精度。
| [1] |
Tenzer R, Chen W J, Jin S G. Effect of Upper Mantle Density Structure on Moho Geometry[J]. Pure and Applied Geophysics, 2015, 172(6): 1 563-1 583 DOI:10.1007/s00024-014-0960-2
(  0) 0) |
| [2] |
Yunck T P, Wu S C, Wu J T, et al. Precise Tracking of Remote Sensing Satellites with the Global Positioning System[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(1): 108-116 DOI:10.1109/36.45753
(  0) 0) |
| [3] |
Bock H, Jäggi A, Švehla D. Precise Orbit Determination for the GOCE Satellite Using GPS[J]. Advances in Space Research, 2007, 39(10): 1 638-1 647 DOI:10.1016/j.asr.2007.02.053
(  0) 0) |
| [4] |
Zehentner N. Kinematic Orbit Positioning Applying the Raw Observation Approach to Observe Time Variable Gravity[D]. Graz: Graz University of Technology, 2016
(  0) 0) |
| [5] |
李建成, 张守建, 邹贤才, 等. GRACE卫星非差运动学厘米级定轨[J]. 科学通报, 2009, 54(16): 2 355-2 362 (Li Jiancheng, Zhang Shoujian, Zou Xiancai, et al. Precise Orbit Determination for GRACE with Zero-Difference Kinematic Method[J]. Chinese Science Bulletin, 2009, 54(16): 2 355-2 362)
(  0) 0) |
| [6] |
Yunck T P, Wu S C. Non-Dynamic Decimeter Tracking of Earth Satellites Using the Global Positioning System[C]. 24th Aerospace Sciences Meeting, Reston, 1986
(  0) 0) |
| [7] |
杨帆, 王长青, 许厚泽, 等. 利用运动学轨道提高GRACE时变重力场解算[J]. 地球物理学报, 2017, 60(1): 37-49 (Yang Fan, Wang Changqing, Hsu Houtse, et al. Towards a More Accurate Temporal Gravity Model from GRACE Observations through the Kinematic Orbits[J]. Chinese Journal of Geophysics, 2017, 60(1): 37-49)
(  0) 0) |
| [8] |
Teunissen P J G, Montenbruck O. Springer Handbook of Global Navigation Satellite Systems[M]. Cham: Springer International Publishing, 2017
(  0) 0) |
| [9] |
Montenbruck O, Gill E, Kroes R. Rapid Orbit Determination of LEO Satellites Using IGS Clock and Ephemeris Products[J]. GPS Solutions, 2005, 9(3): 226-235 DOI:10.1007/s10291-005-0131-0
(  0) 0) |
| [10] |
蔡艳辉, 程鹏飞, 李夕银. GPS伪距改正及精密动态单点定位精度分析[J]. 全球定位系统, 2004, 29(2): 11-15 (Cai Yanhui, Cheng Pengfei, Li Xiyin. Pseudo-Range Correction and Kinematic Point Positioning Accuracy[J]. GNSS World of China, 2004, 29(2): 11-15)
(  0) 0) |
| [11] |
Ashby N. Relativity in the Global Positioning System[J]. Living Reviews in Relativity, 2003, 6(1)
(  0) 0) |
| [12] |
Zehentner N, Mayer-Gürr T. Precise Orbit Determination Based on Raw GPS Measurements[J]. Journal of Geodesy, 2016, 90(3): 275-286 DOI:10.1007/s00190-015-0872-7
(  0) 0) |
| [13] |
Wu J T, Wu S C, Hajj G A, et al. Effects of Antenna Orientation on GPS Carrier Phase[C]. Advances in the Astronautical Sciences, Durango, 1992
(  0) 0) |
| [14] |
陈俊平. 低轨卫星精密定轨研究[D]. 上海: 同济大学, 2007 (Chen Junping. Precise Orbit Determination of Low Earth Orbiters[D]. Shanghai: Tongji University, 2007)
(  0) 0) |
| [15] |
张守建, 李建成, 邹贤才, 等. GRACE卫星精密定轨随机模型精化[J]. 地球物理学报, 2010, 53(7): 1 554-1 561 (Zhang Shoujian, Li Jiancheng, Zou Xiancai, et al. The Stochastic Model Refinement for Precise Orbit Determination of GRACE[J]. Chinese Journal of Geophysics, 2010, 53(7): 1 554-1 561)
(  0) 0) |
| [16] |
秦显平, 杨元喜. LEO星载GPS双向滤波定轨研究[J]. 武汉大学学报: 信息科学版, 2009, 34(2): 231-235 (Qin Xianping, Yang Yuanxi. GPS-Based Orbit Determination for LEO Using Bidirectional Filter[J]. Geomatics and Information Science of Wuhan University, 2009, 34(2): 231-235)
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China;
3. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
4. Hubei Luojia Laboratory, 129 Luoyu Road, Wuhan 430079, China;
5. College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2023, Vol. 43
2023, Vol. 43


