2. 航科院(北京)科技发展有限公司,北京市光熙门北里甲31号,100028
随着移动互联网技术的迅速发展,越来越多的场景需要使用位置服务,定位功能逐步成为智能手机的重要功能。智能手机的定位方式有基站定位、全球导航卫星系统(global navigation satellite system, GNSS)以及多种传感器组合的融合定位等,目前室外定位的主要方法为GNSS定位。早期Android智能手机仅支持直接输出经纬度和高程等位置信息,其定位精度较差,即使在观测条件良好的情况下,定位精度也仅为5~10 m[1],难以满足实际需求。2016年起,谷歌公司在Android 7.0及以上版本设备上开放了可以获取GNSS原始观测值的应用程序接口(application programming interface, API)[2],开发者可以通过调用API实时获取Android智能手机的GNSS伪距、载波相位、多普勒等原始观测值数据,这使得智能手机的高精度定位成为可能。
GNSS观测值质量是影响定位精度的主要因素,国内外许多学者对智能手机GNSS原始观测值质量进行研究,结果表明,智能手机信噪比较低,其与卫星高度角的相关性也较差,需要采用新的随机模型对观测值进行定权[3-5]。与此同时,部分学者也采用各种方法对智能手机GNSS定位性能进行评估。在单频PPP解算中,一般采用经验模型来改正电离层和对流层延迟,其定位精度达到亚米级;在双频PPP解算中,静态定位精度达dm级,动态定位精度达m级[6-7]。总体上看,PPP定位精度和收敛时间不太理想。
因此,本文拟采用Xiaomi 8智能手机,首先对其GPS/BDS伪距观测值数据质量进行分析,并确定一个精确且通用的随机模型,通过SPP解算验证其效果,同时引入国际GNSS服务组织(international GNSS service,IGS)发布的全球电离层格网模型(GIM)产品和Saastamoinen模型,对单频PPP估计中的电离层和对流层参数进行约束,以提高定位精度和缩短定位时间。
1 Android智能手机原始观测值获取在Android 7.0及以上版本中,可通过GNSSClock和GNSSMeasurement类中相关字段来计算GNSS时间、伪距、载波相位和多普勒等观测值,相关字段如表 1和表 2所示[2]。
|
|
表 1 GNSSClock类相关字段 Tab. 1 Relevant fields of GNSSClock class |
|
|
表 2 GNSSMeasurement类字段 Tab. 2 Relevant fields of GNSSMeasurement class |
GPS参考时间为:
| $ \begin{gathered} \text { GPSTime }=\text { TimeNanos }- \\ (\text { FullBiasNanos }+ \text { BiasNanos }) \end{gathered} $ | (1) |
伪距观测值为:
| $ P=\left(t_{R x}-t_{T x}\right) \times 10^{-9} \times c $ | (2) |
式中,c为光速,tRx为信号接收时间,tTx为信号发射时间:
| $ t_{T x}=\text { ReceivedSvTimeNanos } $ | (3) |
| $ \begin{aligned} t_{R x}= & \text { TimeNanos }+ \text { TimeOffsetNanos }- \\ & (\text { FullBiasNanos }+ \text { BiasNanos }) \end{aligned} $ | (4) |
由于手机钟差不稳定,手机本地硬件时钟与GPST的差值会随时间发生变化,为保证时钟偏差的一致性,在计算各历元tRx时,应使用初始历元的FullBiasNanos和BiasNanos值代入计算[8]。
载波相位观测值为:
| $ L=\text { AccumulatedDeltaRangeMeters } $ | (5) |
多普勒观测值为:
| $ D=-\frac{\text { PseudorangeRateMetersPerSecond }}{\lambda} $ | (6) |
式中,λ表示载波波长。
2 智能手机GNSS定位基本原理 2.1 随机模型在GNSS数据处理中,较常用的随机模型主要有卫星高度角模型、信噪比模型。本文同时考虑卫星高度角和信噪比对观测值质量的影响,提出一种联合卫星高度角和信噪比的随机模型。
2.1.1 高度角模型一般而言,卫星高度角越低的观测值,受到的大气延迟和多路径干扰越严重,其信号质量也就越差,可将卫星高度角与观测值噪声方差σ2建立函数模型,本文采用最为常用的三角函数模型[9]:
| $ \sigma^{2}=a+b \frac{1}{\sin (\mathrm{el})^{2}} $ | (7) |
式中,el为卫星高度角,a和b为拟合常数。
2.1.2 信噪比模型信噪比可表征卫星信号强度,能在一定程度上反映卫星信号的质量水平,因此可根据观测值信噪比来确定观测值噪声方差σ2[9]:
| $ \sigma^{2}=a+b \times 10^{-\frac{\mathrm{SNR}}{10}} $ | (8) |
式中,SNR为观测值信噪比,a和b为拟合常数。
2.1.3 联合高度角与信噪比模型鉴于卫星高度角和观测值信噪比均可能对观测值质量造成影响,因此本文同时考虑卫星高度角与观测值信噪比,建立联合高度角与信噪比模型:
| $ \sigma^{2}=a+b \frac{1}{\sin (\mathrm{el})^{2}}+c \times 10^{-\frac{\mathrm{SNR}}{10}} $ | (9) |
式中,el为卫星高度角,SNR为观测值信噪比,a、b、c为拟合常数。
2.2 函数模型目前,大多数智能手机只支持单频GNSS信号接收,只有少量智能手机支持双频卫星信号,因此本文采用单频PPP定位模型,同时将电离层和对流层延迟作为待估参数,并分别使用全球电离层格网模型(GIM)产品和Saastamoinen模型计算的电离层和对流层延迟改正数作为大气估计参数的约束条件[10],模型表达示为:
| $ \left\{\begin{array}{l} P_{\mathrm{r}}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+c \delta t_{\mathrm{r}}-c \delta t^{\mathrm{s}}+M^{\mathrm{s}} \cdot \mathrm{ZTD}_{\mathrm{r}}+ \\ \quad I_{\mathrm{r}}^{\mathrm{s}}+b_{\mathrm{r}}+b^{\mathrm{s}}+\varepsilon_{P_{\mathrm{r}}^{\mathrm{s}}} \\ L_{\mathrm{r}}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+c \delta t_{\mathrm{r}}-c \delta t^{\mathrm{s}}+M^{\mathrm{s}} \cdot \mathrm{ZTD}_{\mathrm{r}}- \\ \quad I_{\mathrm{r}}^{\mathrm{s}}+\lambda N_{\mathrm{r}}^{\mathrm{s}}+B_{\mathrm{r}}+B^{\mathrm{s}}+\varepsilon_{L_{\mathrm{r}}^{\mathrm{s}}} \\ \widetilde{I}_{\mathrm{r}}^{\mathrm{s}}=I_{\mathrm{r}}^{\mathrm{s}}+\varepsilon_{I_{\mathrm{r}}^{\mathrm{s}}} \\ \widetilde{{\rm{Z T D}}_{\mathrm{r}}}=\mathrm{ZTD}_{\mathrm{r}}+\varepsilon_{\widetilde{{\rm{Z T D}}}_{\mathrm{r}}} \end{array}\right. $ | (10) |
式中,Prs表示伪距观测值,Lrs表示载波相位观测值,ρrs表示接收机和卫星之间的几何距离,c为光速,δtv和δts为接收机钟差和卫星钟差,ZTDr为测站r处天顶对流层延迟,Ms为对流层延迟投影函数,Irs为卫星信号在传播过程中的电离层延迟,
选取某大楼楼顶作为数据采集地点,该处环境开阔,观测条件良好。智能手机设备采用Xiaomi 8手机,该设备搭载博通BCM47755芯片,可以提供GPS、GLONASS、BDS和Galileo四个系统L1频率上的观测数据,同时支持GPS和Galileo系统L5和E5a频率上的观测数据。为进行对比分析,在智能手机附近使用测量型接收机Septentrio PolaRx5进行同步观测,两者数据采样间隔均为1 s。其中智能手机参考位置提前由测量型接收机进行高精度测量获得。实验数据采集日期为2022-06-26,为保证实验的可靠性,采集2段实验数据进行分析。
3.2 伪距观测数据质量分析本文通过智能手机与接收机站间单差方法来分析评估智能手机的伪距观测数据质量。在差分观测值中利用智能手机和接收机的参考位置改正站间位置差异,然后通过均值估计站间钟差并进行改正,剩余部分则为伪距噪声和多路径误差。由于接收机伪距噪声远小于智能手机,因此可认为经过改正后的伪距残差主要为智能手机伪距噪声[11]。
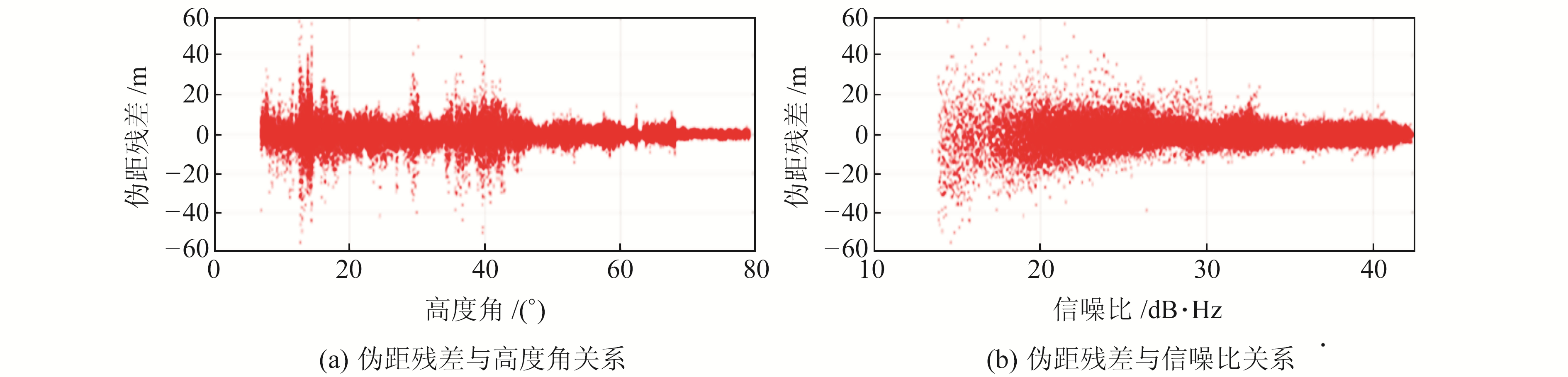
图 1为智能手机伪距残差情况,可以看出,绝大部分卫星的残差在10 m以内,但是部分卫星伪距残差较大,甚至达到60 m。图 2为伪距残差与高度角和信噪比的关系,由图可知,随着高度角增加或信噪比增大,伪距残差均呈现方差逐渐减小的趋势。分别计算伪距残差与高度角和信噪比的相关系数,前者为-0.81,后者为-0.90,说明伪距残差方差与高度角和信噪比均存在极强的负相关性,且与信噪比的相关性更强于与高度角的相关性。由于信噪比和卫星高度角均会影响观测值精度,因此在对卫星观测值进行定权时,同时考虑信噪比和高度角因素更为合理。图 3为智能手机GPS和BDS卫星伪距残差对比,可以看出,GPS卫星伪距残差主要分布在10 m以内,BDS卫星伪距残差主要分布在5 m以内,BDS卫星伪距观测值质量明显优于GPS,因此对于不同导航系统卫星,其随机模型应该分开确定。

|
图 1 智能手机伪距残差 Fig. 1 Pseudorange residuals of smartphone |
|
图 2 智能手机伪距残差与高度角和信噪比关系 Fig. 2 Correlation of pseudorange residuals with elevation angle and SNR of smartphone |

|
图 3 智能手机GPS与BDS伪距残差对比 Fig. 3 Comparison of GPS and BDS pseudorange residuals of smartphone |
本文采用高度角模型、信噪比模型和联合高度角与信噪比模型这3种随机模型分别进行SPP计算,通过定位精度来比较随机模型的效果。实验前对3种随机模型的拟合系数进行标定,考虑到GPS与BDS卫星观测数据质量不一致,因此标定时对GPS和BDS卫星分开拟合模型系数,表 3为3种随机模型的拟合系数。由于时段2伪距质量情况更为复杂,更能表现随机模型的效果,因此采用时段2数据进行SPP计算。SPP观测数据采用单频GPS/BDS数据,卫星轨道和钟差采用广播星历轨道和钟差数据,电离层延迟和对流层延迟分别采用Klobuchar模型和Saastamoinen模型进行改正,地球自转及相对论效应等误差采用相应模型进行改正,参数估计采用最小二乘估计方法。
|
|
表 3 3种随机模型拟合系数 Tab. 3 Fitting coefficients of the three stochastic models |
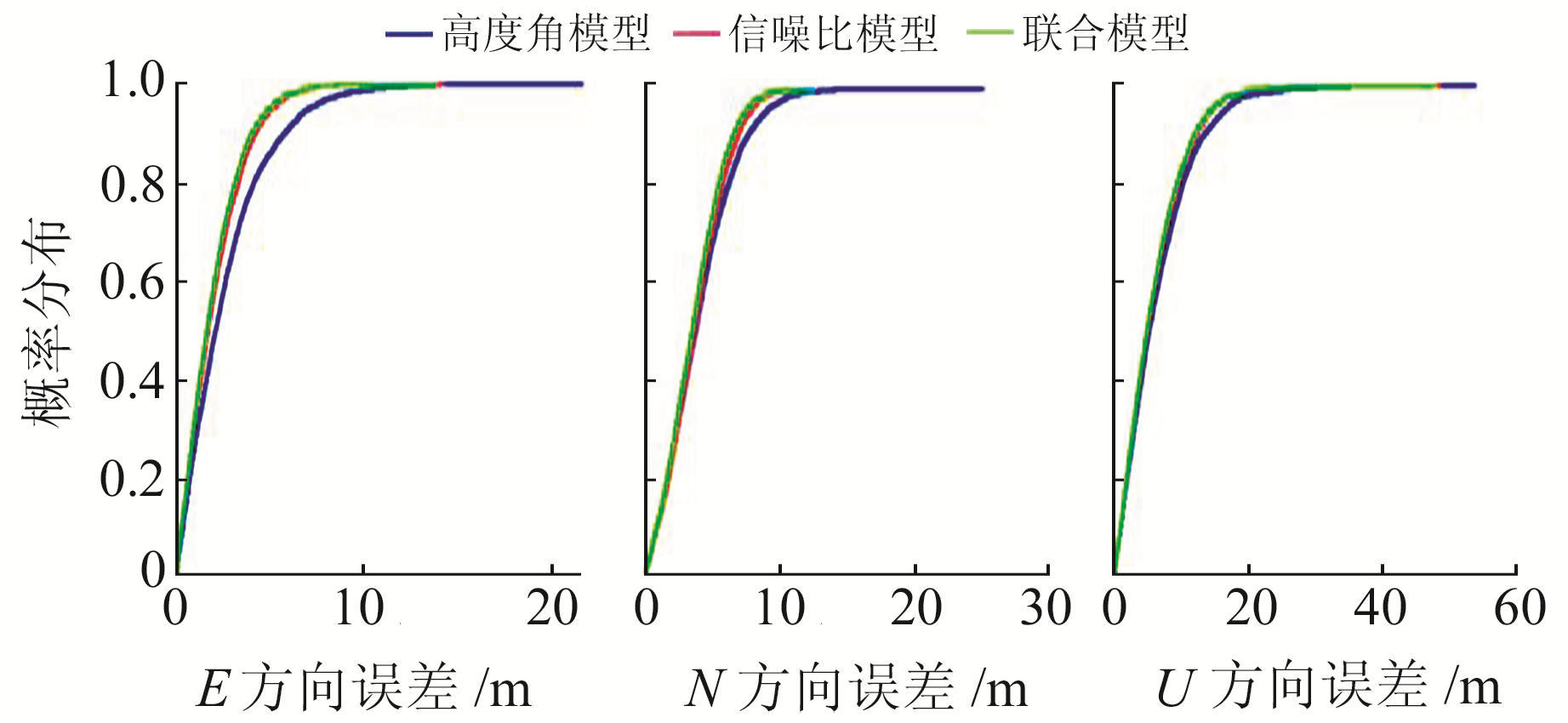
图 4和图 5分别为3种随机模型在E、N、U方向上的定位误差对比和累积分布。可以看出,高度角模型定位精度最差,联合模型定位精度略优于信噪比模型。表 4为3种随机模型定位结果的RMS,可以看出,高度角模型定位精度最差,在E、N、U方向上的定位精度分别为3.57 m、4.85 m、8.60 m;信噪比模型在3个方向上的定位精度分别为2.64 m、4.40 m、7.71 m,比高度角模型定位精度分别提高26%、9%、10%;联合模型在3个方向上的定位精度分别为2.53 m、4.19 m、7.53 m,比高度角模型定位精度分别提高29%、14%、13%。联合高度角与信噪比随机模型优于单一因素随机模型。

|
图 4 3种随机模型定位精度对比 Fig. 4 Comparison of positioning accuracy of the three stochastic models |
|
图 5 3种随机模型定位误差累积分布 Fig. 5 Cumulative distribution of positioning errors of the three stochastic models |
|
|
表 4 3种随机模型定位精度 Tab. 4 Positioning accuracy of the three stochastic models |
由于智能手机双频可见卫星数量稀少且智能手机噪声较大,因此PPP函数模型采用单频PPP非差非组合模型,PPP随机模型分别采用高度角模型、信噪比模型和联合高度角与信噪比模型进行计算。在PPP定位中,观测数据采用单频GPS/BDS数据,轨道和钟差采用国际GNSS服务组织(IGS)发布的事后精密轨道和钟差产品,电离层延迟和对流层延迟分别附加参数进行估计,相位缠绕、地球自转等误差采用对应模型进行改正,卫星端伪距硬件延迟采用IGS发布的差分码偏差(DCB)产品进行改正,其他误差则在进行PPP浮点解算时被相应参数吸收。由于需要估计大气误差参数,估计参数较多,收敛缓慢,因此引入外部的大气产品和模型对大气参数估计进行约束。对于电离层延迟参数,采用IGS发布的全球电离层格网模型产品进行约束,该产品可预报2 d,预报产品精度约为0.5 m[12];对于对流层延迟参数,采用Saastamoinen模型进行约束,该模型精度约为0.1 m。
表 5为2段数据分别采用3种随机模型进行PPP计算的定位结果。从定位精度来看,时段1数据联合模型的定位精度相比于另外两种模型在水平和高程方向上提高约5 cm,时段2数据由于伪距质量情况更为复杂,联合模型的定位精度提升效果更加明显,在水平方向上提高数cm,高程方向上提高2~3 dm。从收敛时间来看,由于时段1数据伪距质量优于时段2,因此时段1数据3种模型定位结果的收敛速度均优于时段2,对于同一段数据,联合模型定位结果的收敛速度明显快于高度角模型和信噪比模型。可以看出,联合模型在定位精度和收敛时间上均优于另外两种随机模型。
|
|
表 5 PPP定位结果 Tab. 5 PPP results |
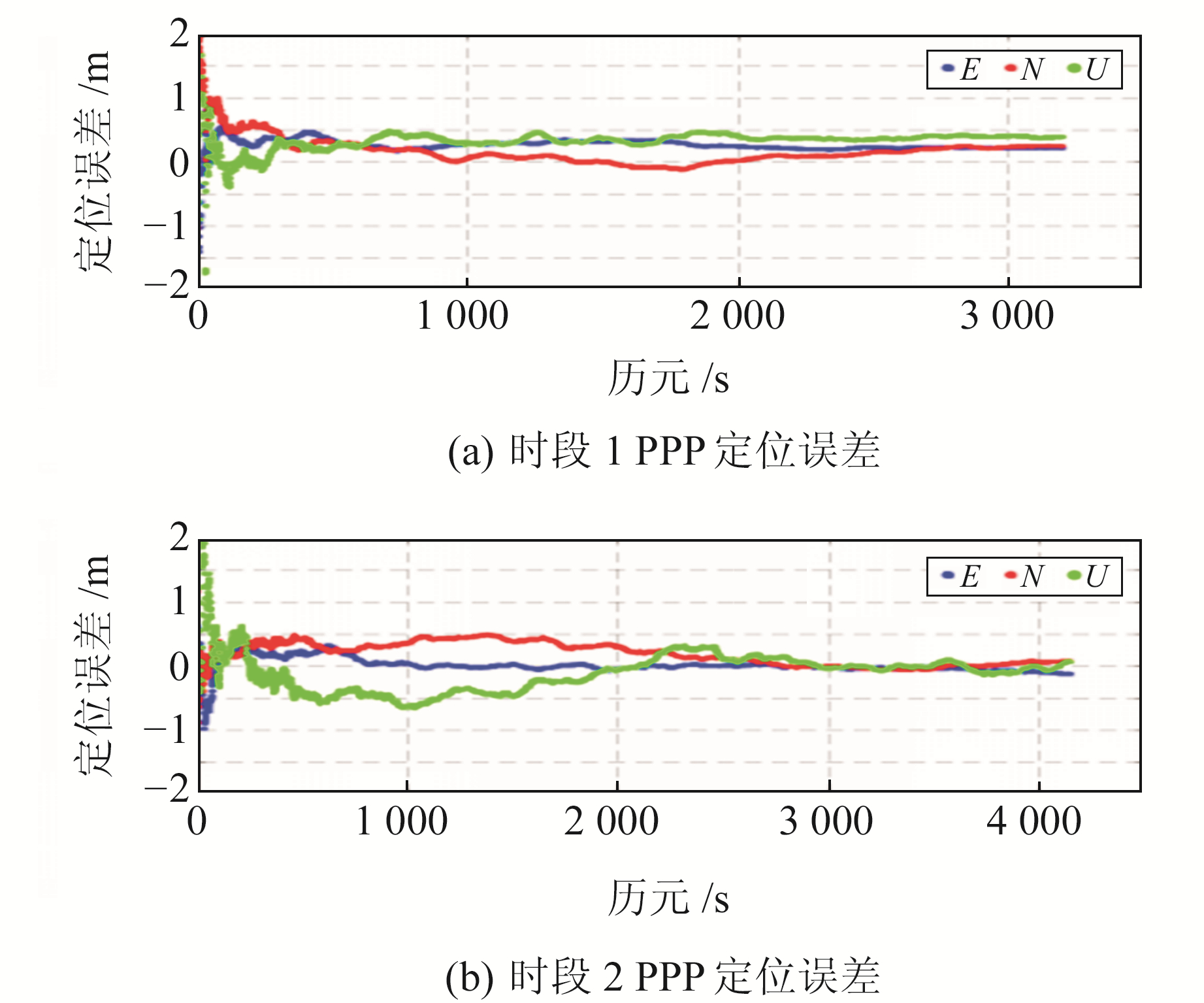
图 6为联合高度角与信噪比模型PPP定位误差。由图可知,时段1数据PPP定位误差收敛迅速,在0.5 min收敛到1 m以内,5 min定位误差收敛到0.5 m以内,E、N、U三个方向上RMS分别为0.24 m、0.15 m、0.42 m。时段2数据PPP定位误差收敛稍慢,水平定位误差在0.1 min收敛到1 m以内,约1.1 min收敛到0.5 m以内,但在高程方向上收敛到1 m需要1 min,收敛到0.5 m则需要约19.3 min。时段2数据E、N、U方向上RMS分别为0.12 m、0.25 m、0.35 m。两段数据最终的定位精度在水平方向上均优于0.2 m,高程方向上均优于0.3 m。以上结果表明,在后处理模式中,智能手机单频PPP可以在较短时间内实现dm级定位结果。
|
图 6 智能手机联合模型PPP定位误差 Fig. 6 PPP error of smartphone with stochastic model |
本文通过Xiaomi 8智能手机获取原始观测值,对智能手机伪距观测数据质量进行分析,通过计算智能手机伪距残差方差与卫星高度角和观测值信噪比的相关系数发现,智能手机伪距残差与高度角和信噪比均具有较强的相关性,采用联合高度角与信噪比的随机模型更为合理;同时,智能手机BDS卫星伪距残差明显小于GPS卫星,不同导航系统卫星的随机模型需要分开确定。基于智能手机实际数据,分别采用SPP及单频PPP模型,对联合高度角和信噪比模型、高度角模型、信噪比模型的定位性能进行比较分析。结果表明,在SPP定位模式下,联合高度角与信噪比模型的定位精度优于单一因素模型,在单频PPP模式下,联合模型的定位精度和收敛时间均优于单一因素模型。在附加电离层和对流层约束的单频PPP后处理解算模式下,智能手机1 min定位精度可收敛至1 m以内,5 min水平方向定位精度优于0.5 m,最终水平方向和高程方向定位精度分别优于0.2 m和0.3 m,表明智能手机后处理可以快速实现dm级定位。
| [1] |
毕京学, 甄杰, 郭英. Android手机GPS和A-GPS定位精度分析[J]. 测绘通报, 2016(7): 10-13 (Bi Jingxue, Zhen Jie, Guo Ying. Accuracy of GPS and A-GPS Positioning on Android Phone[J]. Bulletin of Surveying and Mapping, 2016(7): 10-13)
(  0) 0) |
| [2] |
European GNSS Agency. White Paper on Using GNSS Raw Measurements on Android Devices[S]. 2017
(  0) 0) |
| [3] |
Robustelli U, Baiocchi V, Pugliano G. Assessment of Dual Frequency GNSS Observations from a Xiaomi Mi 8 Android Smartphone and Positioning Performance Analysis[J]. Electronics, 2019, 8(1)
(  0) 0) |
| [4] |
张垠, 涂锐, 洪菊, 等. Android智能手机GNSS数据质量分析[J]. 全球定位系统, 2021, 46(4): 85-92 (Zhang Yin, Tu Rui, Hong Ju, et al. Quality Assessment of Android Smartphone with GNSS Raw Observations[J]. GNSS World of China, 2021, 46(4): 85-92)
(  0) 0) |
| [5] |
Liu W K, Shi X, Zhu F, et al. Quality Analysis of Multi-GNSS Raw Observations and a Velocity-Aided Positioning Approach Based on Smartphones[J]. Advances in Space Research, 2019, 63(8): 2 358-2 377 DOI:10.1016/j.asr.2019.01.004
(  0) 0) |
| [6] |
Gill M, Bisnath S, Aggrey J, et al. Precise Point Positioning(PPP) Using Low-Cost and Ultra-Low-Cost GNSS Receivers[C]. The 30th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, 2017
(  0) 0) |
| [7] |
Elmezayen A, El-Rabbany A. Precise Point Positioning Using World's First Dual-Frequency GPS/Galileo Smartphone[J]. Sensors, 2019, 19(11)
(  0) 0) |
| [8] |
Zangenehnejad F, Gao Y. GNSS Smartphones Positioning: Advances, Challenges, Opportunities, and Future Perspectives[J]. Satellite Navigation, 2021, 2(1)
(  0) 0) |
| [9] |
葛于祥, 刘赞, 李增科, 等. 智能手机单点定位随机模型与平滑方式分析[J]. 合肥工业大学学报: 自然科学版, 2022, 45(8): 1 113-1 119 (Ge Yuxiang, Liu Zan, Li Zengke, et al. Analysis of Stochastic Models and Smoothing Methods in Smartphone Single Point Positioning[J]. Journal of Hefei University of Technology: Natural Science, 2022, 45(8): 1 113-1 119)
(  0) 0) |
| [10] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[D]. 上海: 华东师范大学, 2018 (Zhou Feng. Theory and Methodology of Multi-GNSS Undifferenced and Uncombined Precise Point Positioning[D]. Shanghai: East China Normal University, 2018)
(  0) 0) |
| [11] |
史翔. 基于智能手机GNSS观测值的连续平滑定位算法[D]. 武汉: 武汉大学, 2019 (Shi Xiang. Continuous Smoothing Positioning Algorithm Based on GNSS Observations of Smartphones[D]. Wuhan: Wuhan University, 2019)
(  0) 0) |
| [12] |
盛传贞, 张京奎, 张宝成. 不同全球电离层格网产品在中国区域的应用精度评估与分析[J]. 全球定位系统, 2021, 46(4): 8-15 (Sheng Chuanzhen, Zhang Jingkui, Zhang Baocheng. Evaluation and Analysis of Different Global Ionospheric Maps over China[J]. GNSS World of China, 2021, 46(4): 8-15)
(  0) 0) |
2. Hangke Technology Development Co Ltd, A31 Guangximenbeili, Beijing 100028, China
 2023, Vol. 43
2023, Vol. 43

