2. 千寻位置网络有限公司,上海市国权北路1688弄,200438
GNSS具有操作简单、全天候观测、测站间无需通视等优点,初期主要用于监测地壳运动、地震与火山喷发等[1-3],当前GNSS技术已广泛应用于大坝、滑坡、地面沉降等工程变形监测,成为一种常规的技术手段[4-6],对防灾减灾具有重要意义。GNSS精确可靠的定位结果与观测数据质量密不可分[7],观测数据质量主要与观测环境以及终端设备自身性能有关[8-10]。在水利水电等工程领域,观测环境通常比较复杂,有深山峡谷、密林水域、电磁辐射等不利场景,导致观测数据质量差,定位结果易出现粗差[11-12]。高可靠的定位结果是进行变形分析、制定防灾减灾策略的前提,粗差信息会对变形分析产生干扰。为了更加精准地掌握监测对象的变形动态,需要一种评价指标来评估定位结果的质量,以辅助用户判断成果可靠性。当前常用的GNSS定位结果质量评定指标有方差比(Ratio值)、均方根误差(RMSE)、数据剔除率及定位精度因子(PDOP)等。但GNSS定位解算过程复杂,单一指标或将多种指标简单结合无法有效表征GNSS定位解算结果的质量。基于此,本文针对大坝场景,在分析影响GNSS定位结果质量的各类因素基础上,基于变异系数定权方法,将各单一影响因素指标归一化处理后组合构成一种GNSS定位结果质量评价指标。实例分析表明,该指标准确率较高,是一种实用的GNSS定位结果质量评价指标,可应用于工程实践。
1 GNSS定位结果质量相关因素分析在实际应用中,解算结果的质量或可用性常取决于观测数据质量的好坏、数据解算采用的算法策略、基线距离长短及数据时长等因素。
1.1 原始观测数据质量GNSS定位解算结果质量与原始观测数据质量密不可分,表征原始观测数据质量的关键指标主要包括数据完整率、数据周跳比、平均多路径误差、平均信噪比等。
1) 数据完整率
数据完整率为观测时段内接收机观测到的实际有效观测数据量与理论观测数据量的比值,可反映环境遮挡情况,比率越大越好。单频点数据完整率和单系统数据完整率公式如下:
| $ \mathrm{DI}_f=\left(\sum\limits_{j=1}^n H_f^j / \sum\limits_{j=1}^n E_f^j\right) \times 100 \% $ | (1) |
| $ \mathrm{DI}_s=\left(\sum\limits_{j=1}^n H_s^j / \sum\limits_{j=1}^n E_s^j\right) \times 100 \% $ | (2) |
式中,DIf为单频点观测数据完整率,n为观测时段内理论卫星总数,Hfj为第j颗卫星在观测时段内某频点的有效观测值实际数,Efj为第j颗卫星在观测时段内某频点的有效观测值理论数,DIs为单系统观测数据完整率,Hsj为第j颗卫星在观测时段内所有频点的平均有效观测值实际数,Esj为第j颗卫星在观测时段内所有频点的平均有效观测值理论数。
2) 数据周跳比
数据周跳比为观测时段内接收机观测到的实际有效观测值数与发生周跳历元数据量的比值,可反映周跳发生的平均观测值数,用来表征设备对卫星信号跟踪的连续性情况,比率越大越好,公式如下:
| $ \text { oslip }=\frac{\text { obs }_{\text {have }}}{\text { slip }} $ | (3) |
式中,oslip为周跳比,obshave为有效观测值数,slip为周跳数。
3) 平均多路径误差
多路径误差是指由非视距信号引入的测距误差[13],载波相位测量的多路径误差小于波长的1/4,远小于伪距多路径误差,因此研究重点为伪距多路径误差,其计算公式如下:
| $ \left\{\begin{array}{l} \mathrm{MP}_i=\rho_i-\frac{f_i^2+f_j^2}{f_i^2-f_j^2} \varphi_i+\frac{2 f_j^2}{f_i^2-f_j^2} \varphi_j \\ \mathrm{MP}_j=\rho_j-\frac{2 f_i^2}{f_i^2-f_j^2} \varphi_i+\frac{f_i^2+f_j^2}{f_i^2-f_j^2} \varphi_j \end{array}\right. $ | (4) |
式中,MPi、MPj为包含多路径误差和整周模糊度的计算量,ρi、ρj为伪距观测量,φi、φj为载波相位观测量,fi、fj为频率。
同一颗卫星在连续观测且无周跳情况下组合的模糊度参数不会发生变化,在无周跳的多个历元间按式(5)进行计算,得到平均多路径误差:
| $ \overline{\mathrm{MP}}_k=\sqrt{\frac{1}{n-1} \sum\limits_{i=1}^n\left(\mathrm{MP}_k^t-\frac{\sum\limits_{i=1}^n \mathrm{MP}_k^t}{n}\right)^2} $ | (5) |
式中,MPk为接收机观测到的卫星在k频率上多路径误差的评估值;n为滑动窗口的历元数,默认为50;MPkt为历元t时刻接收机观测到的卫星在频率k上包含多路径误差和整周模糊度信息的计算量。
4) 平均信噪比
平均信噪比可表征设备捕获的信号强度,数值越大越好,公式如下:
| $ \overline{\mathrm{SNR}}=\frac{1}{n} \sum\limits_{j=1}^n\left(\frac{1}{N_j} \sum\limits_{i=1}^{N_j} \mathrm{SNR}_j^t\right) $ | (6) |
式中,SNR为卫星平均信噪比指标统计值,n为观测卫星总数,j为观测卫星号,Nj为卫星j的观测历元总数,i为卫星j的观测历元序号,SNRjt为卫星j在历元t的信噪比观测值。
1.2 数据处理算法及策略GNSS定位结果质量同样与数据处理算法及策略有关。数据处理算法中不同函数模型、随机模型、误差改正模型都会导致结果出现差异,而不同数据采样间隔、截止高度角同样会使解算结果产生差异。数据处理算法及策略对解算结果质量的影响无法定量分析,通常情况下采用Ratio值、RMSE、数据剔除率以及PDOP等数据解算特征信息来表示:Ratio值为整周模糊度固定时次优整数解方差与最优整数解方差的比值,可反映整周模糊度可靠性的高低,数值越大表明可靠性越高;RMSE可反映观测值质量,数值越小表明定位结果质量越高;数据剔除率是指定位解算过程中未采用的观测值个数与获取的同类观测值总数的比值,可表征原始观测值的稳定性及精度,数值越高表明观测值质量越差;PDOP值可表征定位时所跟踪卫星在空间分布的几何强度对三维定位精度的影响,数值越小表明卫星分布的几何强度和定位精度越高。上述评价指标从模糊度可靠性、观测值质量、数据利用率以及卫星几何强度等方面来判定GNSS定位解算质量,均无法直接准确评价GNSS定位结果质量。
1.3 基线距离与数据时长由于基线距离长、站间高程差异大,会使基线两端对流层特征相似度降低,通过差分方式很难有效消除全部的对流层延迟,对定位精度的影响较大,特别是对高程精度的影响。此外,不同观测时段长度也会影响基线解算精度。一般情况下,观测时段越长,基线解算精度越高,但当观测环境较差时,观测时间越长,基线解算精度不一定越高。其原因为同一观测环境下不同观测时段的数据质量不同:数据质量较好时,较短时间内的观测数据就能获得较高精度的基线解算结果;相反,若其中某些时段的观测数据质量较差,即使观测时间很长,基线解算也可能会失败,这主要是由于数据质量较差的这部分数据将使周跳探测与修复发生错误。
2 综合评价指标构建及算法步骤综合考虑各类因素对结果精度的影响,利用变异系数定权方法,将多种指标进行线性组合,用于评价GNSS定位结果质量。
2.1 单一评价指标选取通过比较研究,本文选取与原始数据质量、数据解算特征信息、基线距离和观测时长相关的11个指标,具体见表 1。
|
|
表 1 评估项目 Tab. 1 The evaluation item |
由于不同指标的变化趋势和变化范围可能不一致,因此无法对多个指标进行简单结合,需对其进行归一化处理,从而成为纯量。具体步骤如下:
1) 指标同趋势化:在综合指标体系中,当数据完整率越大、多路径数值越小时,观测数据质量越高,因此需将数据完整率指标按照取倒数方法将其极大型指标值转化为极小型。
2) 指标无量纲化:综合评价体系中各指标值必须均为无量纲数值,通常按照式(7)对同趋势化后的各指标值进行处理:
| $ Q_l=\frac{x_l-\operatorname{Min}_l}{\operatorname{Max}_l-\operatorname{Min}_l} $ | (7) |
式中,Ql为指标无量纲化后第l项指标值,xl为同趋势化后第l项指标值,Minl为第l项指标的最小值,Maxl为第l项指标的最大值。
3) 指标权重系数确定:不同指标的权重不同,因此需对其进行赋权操作。本文采用变异系数定权法[14]进行赋权。变异系数又称标准差率,是标准差与均值的比值,可客观反映指标数值的变异程度。其基本思想是变异系数越大的指标(越难以实现的指标)更能反映被评价单位的差距,因此其权重也越大[15-16]。具体定权过程可表示为:
| $ \mathrm{CV}_l=\frac{\sigma_l}{\mu_l} $ | (8) |
| $ W_l=\frac{\mathrm{CV}_l}{\sum\limits_{j=1}^n \mathrm{CV}_j} $ | (9) |
式中,CV为变异系数,W为基于变异系数定权的权值,σ和μ分别为标准差操作与均值操作。
通过线性组合方法得到综合评价指标T:
| $ T=\sum\limits_{i=1}^{N_l} w_i \cdot Q_i $ | (10) |
式中,Nl为单项指标个数,本文设置为11;wi和Qi分别为第i项指标的权值和无量纲化后指标。
2.3 算法步骤综合评价指标计算方法如下:
1) 利用式(1)~(5)对GNSS原始观测数据进行质量评估,获取原始观测数据质量的相关指标值;
2) 对GNSS数据基线进行解算,获取基线解算结果、基线解算特征信息、基线距离高差及数据时长等指标;
3) 对表 1中各项指标进行归一化处理,并基于变异系数进行定权;
4) 将定权后各参数的均方根误差及平滑度进行线性组合,求出T值,T值越小表明监测结果质量越高。
3 工程应用为验证本文方法的有效性,利用实测数据进行测试验证。测试数据来源于一组大坝实测数据,共选取2个GNSS监测点,测点1为库区边坡监测点,测点2为坝体监测点。在测点2上进行移动滑台测试,测试时段内共进行4次滑动实验,现场记录数据如表 2(单位mm)所示。
|
|
表 2 滑动测试记录 Tab. 2 Sliding test record |
数据解算具体配置如下:测试时段为2021-06-28~07-12,共15 d,数据采样间隔为10 s,参与解算的卫星系统为GPS+BDS,解算弧长为4 h,2个测点的坐标残差序列及质量指标序列如图 1、2所示。

|
图 1 测点1评价指标 Fig. 1 Evaluation indicators of measurement point 1 |
|
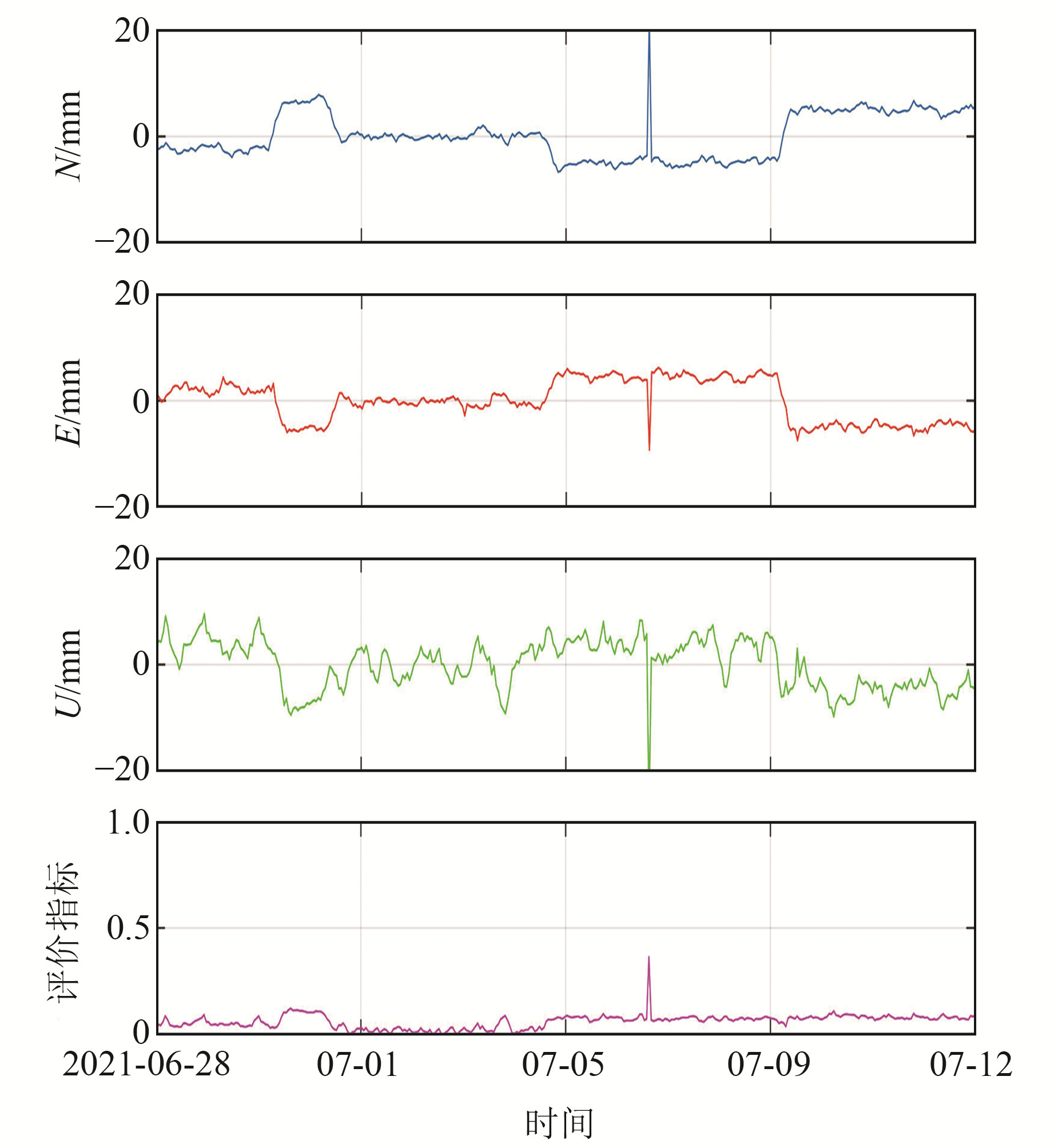
图 2 测点2评价指标 Fig. 2 Evaluation indicators of measurement point 2 |
由图 1、2可知,2个测点的坐标序列整体较为平稳,未发现明显位移情况。测点1在整个测试时段内未出现异常点;测点2在测试时段内进行滑动测试时出现1个跳点,水平和高程偏差均超过20 mm。表 3(单位mm)为具体精度指标,其中测点2数据为修正滑台位移后的统计指标。图 3、4分别为测点2原始数据质量指标及数据解算特征信息。
|
|
表 3 精度统计指标 Tab. 3 Statistics of accuracy indicator |

|
图 3 测点2原始数据质量指标 Fig. 3 Raw data quality indicators of measurement point 2 |
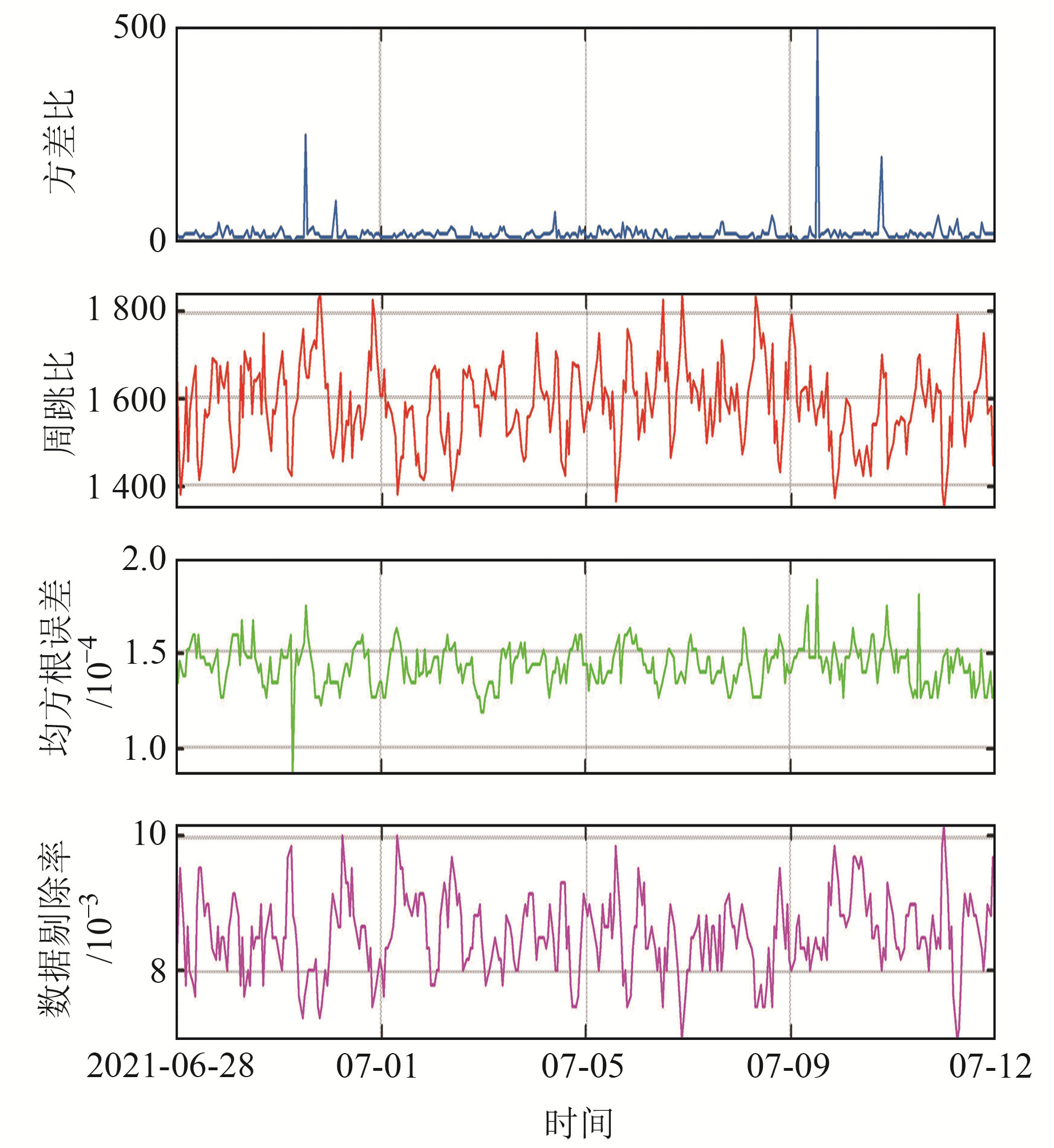
|
图 4 测点2数据解算特征信息 Fig. 4 GNSS data processing feature information of measurement point 2 |
由表 3可知,2个测点在水平精度上均优于1 mm,在高程精度上均优于5 mm。2个测点的综合评价指标均值均小于0.1,说明定位结果质量较好,测点2的综合评价指标最大值出现在跳点时刻,滑台移动时综合指标未出现较大变化。由图 2~4可知,在滑台移动及跳点时刻,测点2的单一指标均无法有效表征定位质量,综合质量指标明显增大,说明综合质量指标可有效反馈测点跳点情况,为监测数据的使用提供依据,表明本文提出的质量评价指标具有可行性,可服务于工程实践。
4 结语本文提出一种GNSS定位结果质量评价指标,即通过变异系数定权法,将归一化后的各单项指标进行线性组合。大坝实测数据分析表明,该方法所确定的质量评估值效果较好,是一种有效的GNSS定位结果质量评价指标,可服务于工程实践,同时可为GNSS定位结果质量评估提供新思路。但此次测试样本较少,后续可增加测试样本以进一步验证算法的可靠性。
| [1] |
Dong D N, Bock Y. Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B4): 3 949-3 966 DOI:10.1029/JB094iB04p03949
(  0) 0) |
| [2] |
Bock Y, Wdowinski S, Fang P, et al. Southern California Permanent GPS Geodetic Array: Continuous Measurements of Regional Crustal Deformation between the 1992 Landers and 1994 Northridge Earthquakes[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18 013-18 033 DOI:10.1029/97JB01379
(  0) 0) |
| [3] |
Dvorak J. Tracking the Movement of Hawaiian Volcanoes: Global Positioning System(GPS) Measurement[J]. Earthquakes and Volcanoes, 1992, 23(6): 255-267
(  0) 0) |
| [4] |
Vazquez-Ontiveros J R, Martinez-Felix C A, Vazquez-Becerra G E, et al. Monitoring of Local Deformations and Reservoir Water Level for a Gravity Type Dam Based on GPS Observations[J]. Advances in Space Research, 2022, 69(1): 319-330 DOI:10.1016/j.asr.2021.09.018
(  0) 0) |
| [5] |
Wang J, Nie G G, Gao S J, et al. Landslide Deformation Prediction Based on a GNSS Time Series Analysis and Recurrent Neural Network Model[J]. Remote Sensing, 2021, 13(6)
(  0) 0) |
| [6] |
陈玉林, 匡翠林, 戴吾蛟, 等. 广州南沙区GPS地面沉降监测数据处理[J]. 大地测量与地球动力学, 2015, 35(5): 849-852 (Chen Yulin, Kuang Cuilin, Dai Wujiao, et al. Land Subsidence Monitoring Using GPS Network in Nansha, Guangzhou[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 849-852 DOI:10.14075/j.jgg.2015.05.027)
(  0) 0) |
| [7] |
戴吾蛟, 谢荣安, 余文坤, 等. 不同观测环境基于基线解算的数据质量分析[J]. 工程勘察, 2012, 40(11): 55-58 (Dai Wujiao, Xie Rongan, Yu Wenkun, et al. Quality Analysis of GNSS Data in Different Environments Based on Baseline Vector Solution[J]. Geotechnical Investigation and Surveying, 2012, 40(11): 55-58)
(  0) 0) |
| [8] |
Li B F. Stochastic Modeling of Triple-Frequency Beidou Signals: Estimation, Assessment and Impact Analysis[J]. Journal of Geodesy, 2016, 90(7): 593-610 DOI:10.1007/s00190-016-0896-7
(  0) 0) |
| [9] |
Luo X G. GPS Stochastic Modelling: Signal Quality Measures and ARMA Processes[M]. Berlin, Heidelberg: Springer, 2013
(  0) 0) |
| [10] |
Yang Y X, Li J L, Wang A B, et al. Preliminary Assessment of the Navigation and Positioning Performance of Beidou Regional Navigation Satellite System[J]. Science China: Earth Sciences, 2014, 57(1): 144-152 DOI:10.1007/s11430-013-4769-0
(  0) 0) |
| [11] |
刘大杰, 陶本藻. 实用测量数据处理方法[M]. 北京: 测绘出版社, 2000 (Liu Dajie, Tao Benzao. Practical Measurement Data Processing Method[M]. Beijing: Surveying and Mapping Press, 2000)
(  0) 0) |
| [12] |
周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115-120 (Zhou Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18(2): 115-120)
(  0) 0) |
| [13] |
Pan L, Guo F, Ma F J. An Improved BDS Satellite-Induced Code Bias Correction Model Considering the Consistency of Multipath Combinations[J]. Remote Sensing, 2018, 10(8)
(  0) 0) |
| [14] |
Dellwo V. Rhythm and Speech Rate: A Variation Coefficient for deltaC[J]. Language and Language-Processing, 2006, 231-241
(  0) 0) |
| [15] |
王永弟, 许承权, 范千. 熵权、变异系数及模糊多准则决策在测量平差中的综合应用[J]. 工程勘察, 2012, 40(9): 58-61 (Wang Yongdi, Xu Chengquan, Fan Qian. Integrated Application of Entropy Theory, Variation Coefficient and Fuzzy Multi-Criteria Decision Making in Surveying Adjustment[J]. Geotechnical Investigation and Surveying, 2012, 40(9): 58-61)
(  0) 0) |
| [16] |
朱建军, 章浙涛, 匡翠林, 等. 一种可靠的小波去噪质量评价指标[J]. 武汉大学学报: 信息科学版, 2015, 40(5): 688-694 (Zhu Jianjun, Zhang Zhetao, Kuang Cuilin, et al. A Reliable Evaluation Indicator of Wavelet De-Noising[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 688-694)
(  0) 0) |
2. Qianxun Spatial Intelligence Co Ltd, 1688 North-Guoquan Road, Shanghai 200438, China
 2023, Vol. 43
2023, Vol. 43

