2. 湖北工业大学土木建筑与环境学院,武汉市南李路28号,430068
由于强震事件的不可重复性与我国强震观测能力分布的不均匀性,以及近场强震观测资料的缺失,导致当前强地震动场的分析存在实测波形不足的困难,前人利用格林函数法、有限断层法及三角级数叠加法等开展强地面运动估计与波形的合成[1-5]。2017-08-08九寨沟M7.0地震是2008年汶川M8.0地震与2013年雅安M7.0地震后四川地区发生的又一次破坏性地震,中国地震局发布的地震烈度分布显示,宏观震中比芒村地震烈度为Ⅸ度,近场PGA达707 Gal。现场建筑结构震害与地质灾害情况揭示,近场强地震动具有较为显著的方向效应特征,即平行断层方向的结构震害显著大于垂直断层方向[6]。
本文基于二维有限单元法使用接触单元模拟断裂带的非连续破裂过程,建立2017-08-08四川九寨沟M7.0地震近场强地面运动估计模型,并对应力降和屈服应力等关键震源参数进行研究。在利用国家强震数据中心提供的实际观测波形开展地震动参数信度检验基础上,给出PGA及仪器地震烈度分布结果,探讨近场强地面运动方向效应特征及其成因机理。通过给出一种具备明确震源物理意义且参数设置简单的强地面运动模拟方法,可在一定程度上克服当前观测能力不足所造成的困难,对近断层强地震动特性研究具有一定的科学意义和理论增量。
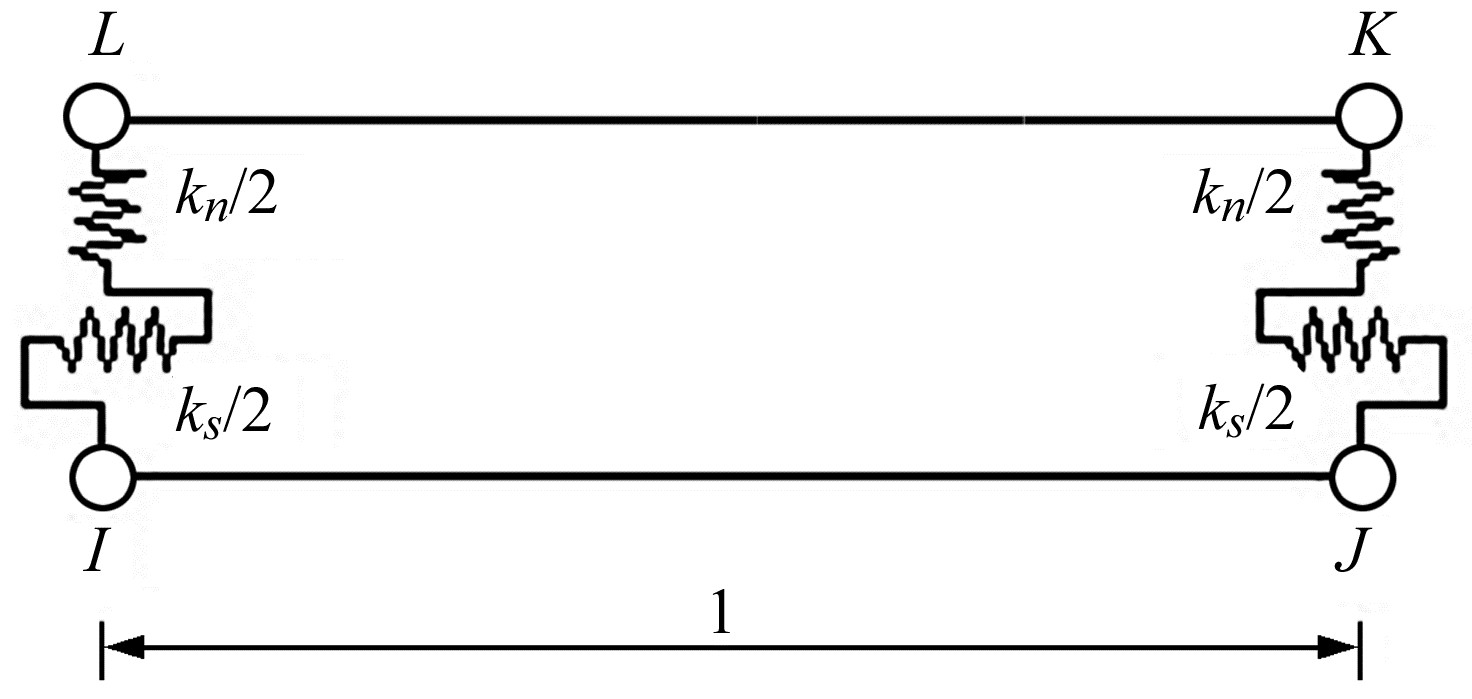
1 基于有限元的地震动模拟方法 1.1 断层面接触模型建立方法发震断层连续破裂过程的运动学方程描述了破裂行为的不连续性,将其作为非线性问题进行处理,分别使用平面应变单元和接触单元模拟孕震区域的基岩和发震断层。使用由2个固体单元组成的Goodman接触单元模拟发震断层[7],具有平行、垂直或旋转等3种不同的运动方式,如图 1所示,当引入拉力时,接触单元将会分离,作用力通过接触面的传递将会被切断[8]。
|
图 1 Goodman接触单元示意图 Fig. 1 Schematic diagram of Goodman contact element |
当动剪切应力达到接触面的剪应力屈服值τy时,单元将会发生滑动。此时,粘聚力C、正应力σ和内摩擦角φ存在以下关系式:
| $ \tau_y=C+\sigma \tan \varphi $ | (1) |
首先求解由重力产生的应力场,其应力分布可表示为:
| $ \{f\}=\int_V \boldsymbol{N}^{\mathrm{T}}\{\boldsymbol{p}\} \mathrm{d} v $ | (2) |
式中,N为形函数矩阵,{p}={0-ρg}T,ρ为密度,g为重力加速度。
假设断层面上由重力产生的剪应力在之前的历史地震事件中被释放,现阶段组成断层的接触单元的剪应力被减小至0。然后在模型两端边界施加构造应力场,通过逐渐增加构造应力,直至接触单元的剪应力到达屈服强度,确定地震事件破裂的临界应力状态,并将其转移到动力分析模型上[9]。
1.3 动力分析为分析断层面上的破裂情况,需考虑滑动和分离现象。动力分析为非线性分析[8],第n时步的运动方程为:
| $ [\boldsymbol{M}]\{\ddot{u}\}_n+[\boldsymbol{C}]\{\dot{u}\}_n+[\boldsymbol{K}]\{u\}_n=\{g(t, s)\} $ | (3) |
式中,M、C、K分别为质量、阻尼及刚度矩阵,{g(t, s)}为由动应力降Δτ计算得到的外力,t和s为滑动发生的时间和节点对。在初始时步(t=0)有:
| $ \{g(0, s)\}=\frac{l \cdot \Delta \tau}{2} $ | (4) |
式中,l为接触单元的长度,在接触单元滑动时剪应力τ为定值,且大小为τ=τy-Δτ,其中τy为屈服应力。将该节点的外力{g(0, s)}施加于破裂起始位置处的节点对上,同时确保外力方向必须与初始剪应力方向一致。施加的节点外力会使应力重新分布,并使相邻接触单元的剪应力增加。
2 九寨沟M7.0地震强地面运动模拟 2.1 九寨沟地震概况2017-08-08九寨沟M7.0地震震中为33.20°N、103.82°E,震源深度约20 km,宏观震中位于九寨沟核心景区西部5 km处的比芒村,震中烈度为Ⅸ度,近场PGA达707 Gal,为左旋走滑型地震。易桂喜等[6]通过研究余震分布认为,该地震发震断层为以左旋走滑为主的NW-SE向树正断裂,长度约38 km。表 1及图 2为九寨沟地区CSMN强震测站、活动断裂及地震序列等相关信息。
|
|
表 1 CSMN台站信息 Tab. 1 Information of CSMN stations |

|
F01:东昆仑断裂;F02:白龙江断裂;F03光盖山-迭山断裂;F04:哈南-青山湾-稻畦子断裂;F05:塔藏断裂;F06:雪山梁子断裂;F07:虎牙断裂;F08:树正断裂;F09:岷江断裂;F10:龙日坝断裂 图 2 九寨沟区域活动断裂、CSMN强震测站及余震序列分布 Fig. 2 The distribution of active faults, CSMN strong earthquake stations and aftershock events in Jiuzhaigou area |
九寨沟地震震源参数为走向152°、倾角88°、滑动角-3°,平均位错1.4 m,应力降8.5 MPa。考虑到发震断层近乎垂直且震源机制为左旋走滑,故将该地震事件简化为二维平面问题。结合区域活动断裂分布,利用接触单元及研究区内活动断裂,建立九寨沟地区强地面运动数值模型,网格划分情况见图 3。

|
图 3 九寨沟地区二维有限元模型 Fig. 3 Two-dimensional finite element model of Jiuzhaigou area |
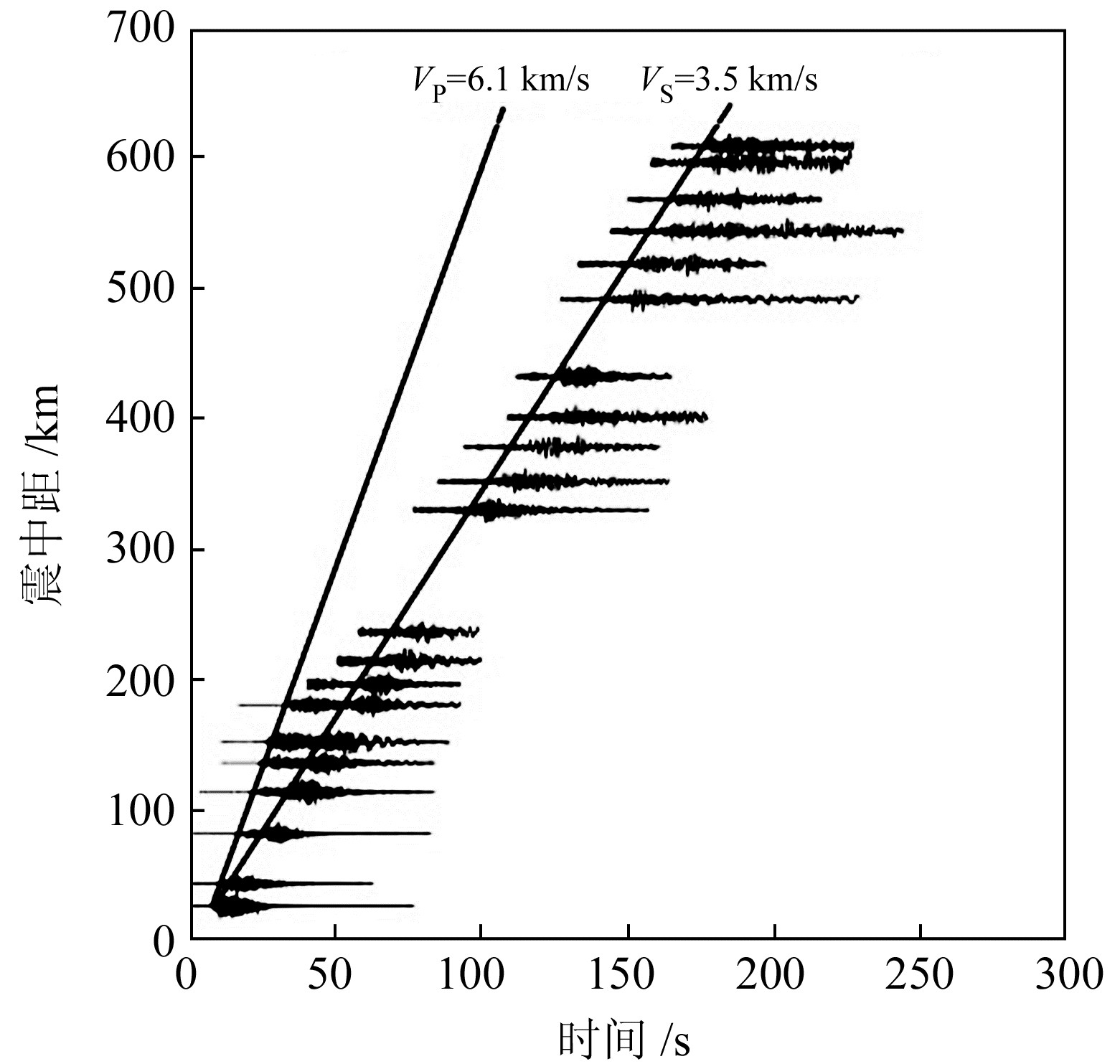
岩体介质的物理力学参数对数值模拟结果具有重要影响,利用国家强震动观测台网中心(CSMN)提供的九寨沟地震观测波形计算建模区P波与S波波速。由图 4可知,研究区测站震中距与弹性波到达时间线性相关,因此将基岩视为弹性均质介质,重度为28.0 kN/m3,泊松比为0.3,VP=6.1 km/s,VS=3.5 km/s,与徐晶等[10]的研究结果基本一致。
|
图 4 九寨沟地区P波及S波波速 Fig. 4 Velocity of P wave and S wave of Jiuzhaigou area |
在假设实际应力降未知的情况下,将应力降范围设为6.0~12.0 MPa,取值间隔为0.5 MPa;将断层接触单元的屈服应力范围设为2.0~5.0 MPa,取值间隔为1.0 MPa。经处理后可获得研究区内水平地表任意位置的地震动加速度波形,将EW向与NS向地震动分量进行矢量合成,获得水平向PGA,则:
| $ \mathrm{PGA}=\max \left(\operatorname{abs}\left(\boldsymbol{a}_h\right)\right) $ | (5) |
| $ \boldsymbol{a}_h=\boldsymbol{a}_{\mathrm{EW}}+\boldsymbol{a}_{\mathrm{NS}} $ | (6) |
式中,ah为某场址处水平向地震动加速度时程;aEW和aNS分别为EW向及NS向地震动加速度分量。
为直观分析不同震源参数对水平向PGA的影响,取九寨百河(51JZB)及平武木座(51PWM)2个台站场址处的PGA计算结果,其中近场九寨百河台(51JZB)震中距约为31.73 km,远场平武木座台(51PWM)震中距约为91.30 km。
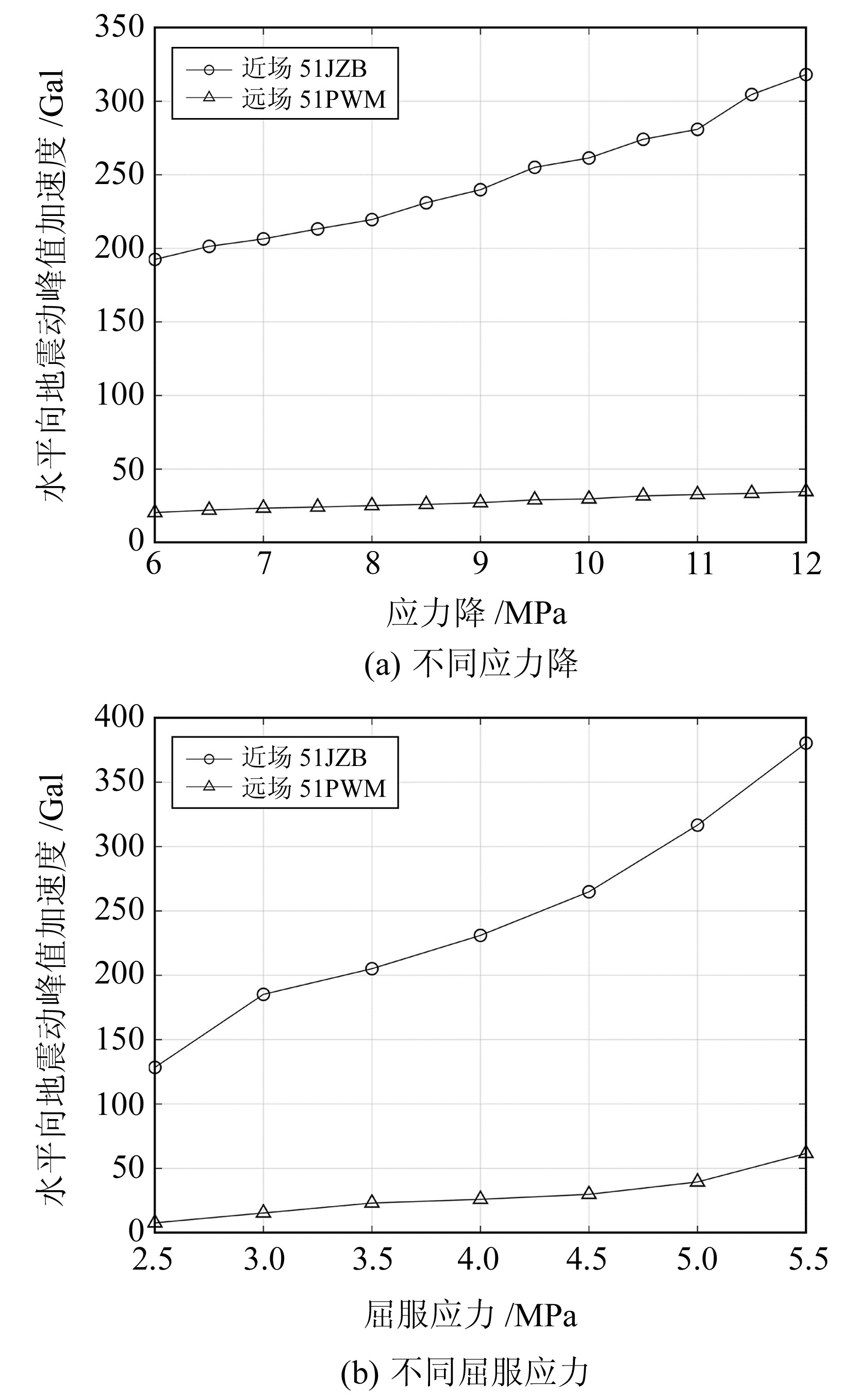
图 5(a)为当屈服应力取值4 MPa时,不同应力降条件下近场及远场PGA的变化情况。由图可见,随着应力降取值由2.5 MPa增大至5.5 MPa,PGA在近场由192.52 Gal增大至318.15 Gal,远场则由20.45 Gal增大至34.77 Gal,说明PGA在整体上随应力降增大的同时,其近场地震动受到的影响较远场更为显著。究其原因可能在于,高频地震动随震中距增大而产生衰减效应,这与李宗超等[11]使用随机有限断层法获得的结论一致。
|
图 5 不同条件下的PGA Fig. 5 PGA under different conditions |
图 5(b)为当应力降取值8.5 MPa时,不同屈服应力条件下近场及远场PGA的变化情况。由图可见,随着屈服应力取值由2.5 MPa增大至5.5 MPa,PGA在近场由128.40 Gal增大至380.44 Gal,远场则由7.71 Gal增大至61.63 Gal。说明随着屈服应力增大,PGA呈现出整体持续增大但远场衰减的变化特征,且其对屈服应力的响应较应力降更加明显。
引入模型偏差k及模型标准差s以分析2类震源参数对水平向PGA的影响[12],表达式为:
| $ k=\frac{1}{n} \sum\limits_{i=1}^n \ln \left(\mathrm{PGA}_{\mathrm{ob}} / \mathrm{PGA}_{\mathrm{simu}}\right) $ | (7) |
| $ s=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(\ln \left(\mathrm{PGA}_{\mathrm{ob}} / \mathrm{PGA}_{\mathrm{simu}}\right)-k\right)^2} $ | (8) |
式中,n为台站数量,k越大表示模拟结果越偏离观测结果,s越大则离散程度越高。
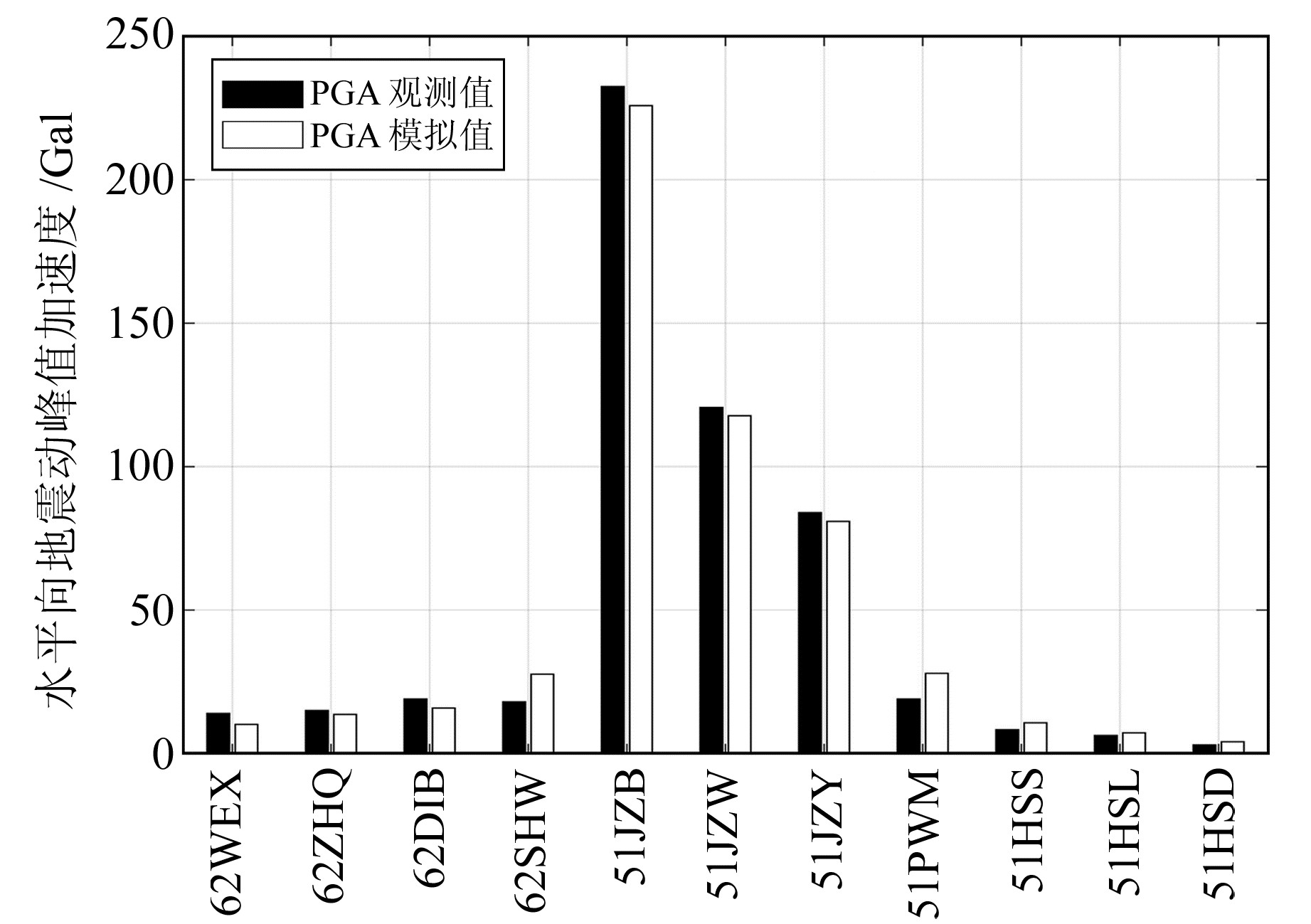
通过对比不同震源参数条件下水平向PGA模拟值与实际观测值的偏差及标准差发现,当屈服应力变化时,PGA偏差约为6.73,标准差约为0.35;而应力降变化时,PGA偏差约为3.24,标准差约为0.46,说明断层接触单元屈服应力与应力降均对PGA具有重要影响,且屈服应力影响更为显著。在震源参数敏感性分析基础上,通过对不同震源参数组合进行试算发现,应力降为8.5 MPa且屈服应力为4.0 MPa时,获得的模拟值与CSMN强震观测结果具有最好的一致性。图 6为该最优震源参数组合下的PGA观测值与模拟值,可以发现,51JZB、51JZY和51JZW 3个近场强震台站场址处的PGA明显高于其他8个远场台站。
|
图 6 最优震源参数组合下的PGA观测值与模拟值 Fig. 6 PGA observations and simulation results under the optimal source parameter combination |
利用相对误差百分比R来评价模拟误差随震中距的变化情况:
| $ R=\left|\mathrm{PGA}_{h, \text { simu }}-\mathrm{PGA}_{h, \mathrm{ob}}\right| / \mathrm{PGA}_{h, \mathrm{ob}} \times 100 \% $ | (9) |
式中,PGAh, simu与PGAh, ob分别表示水平向PGA的模拟值和观测值。
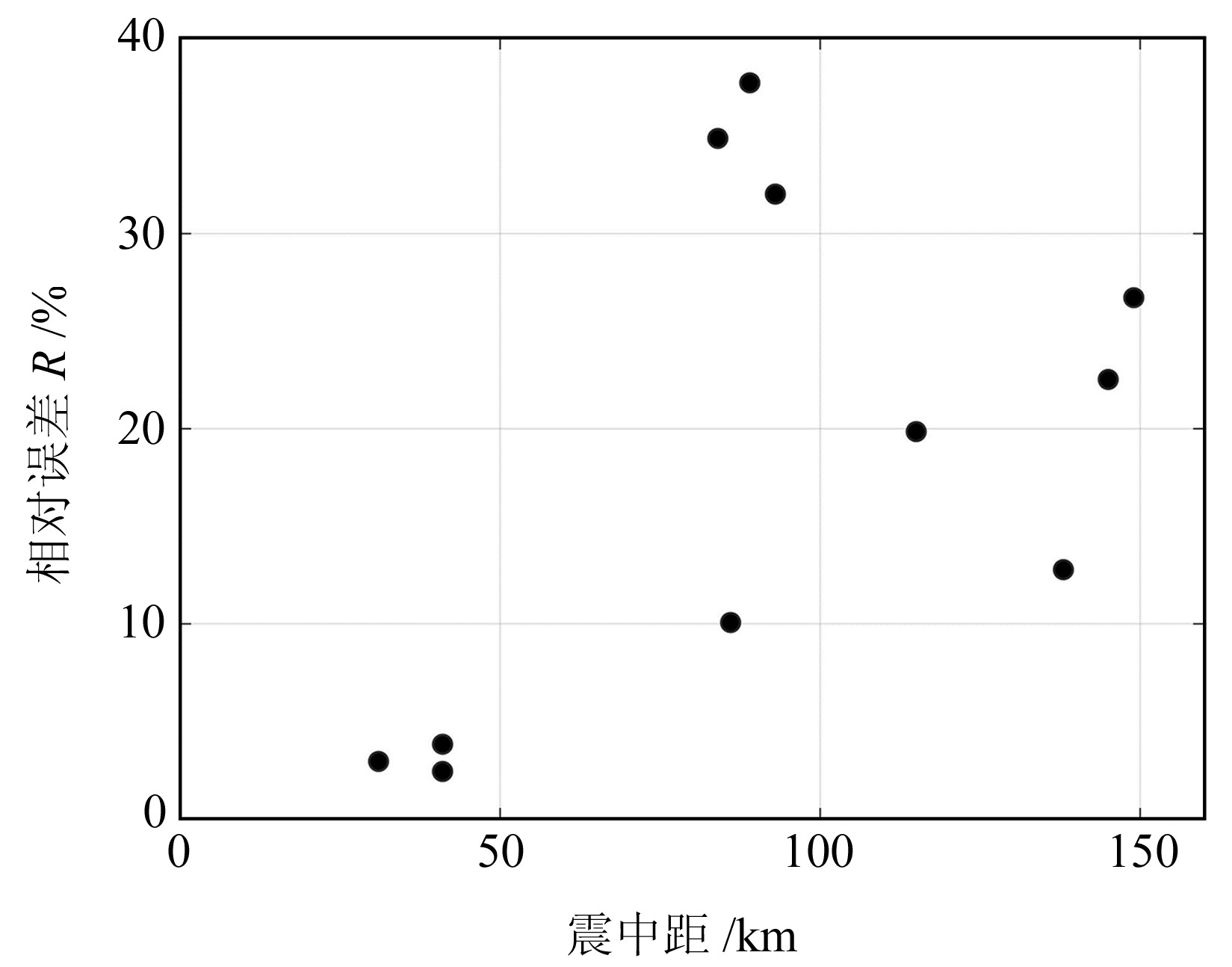
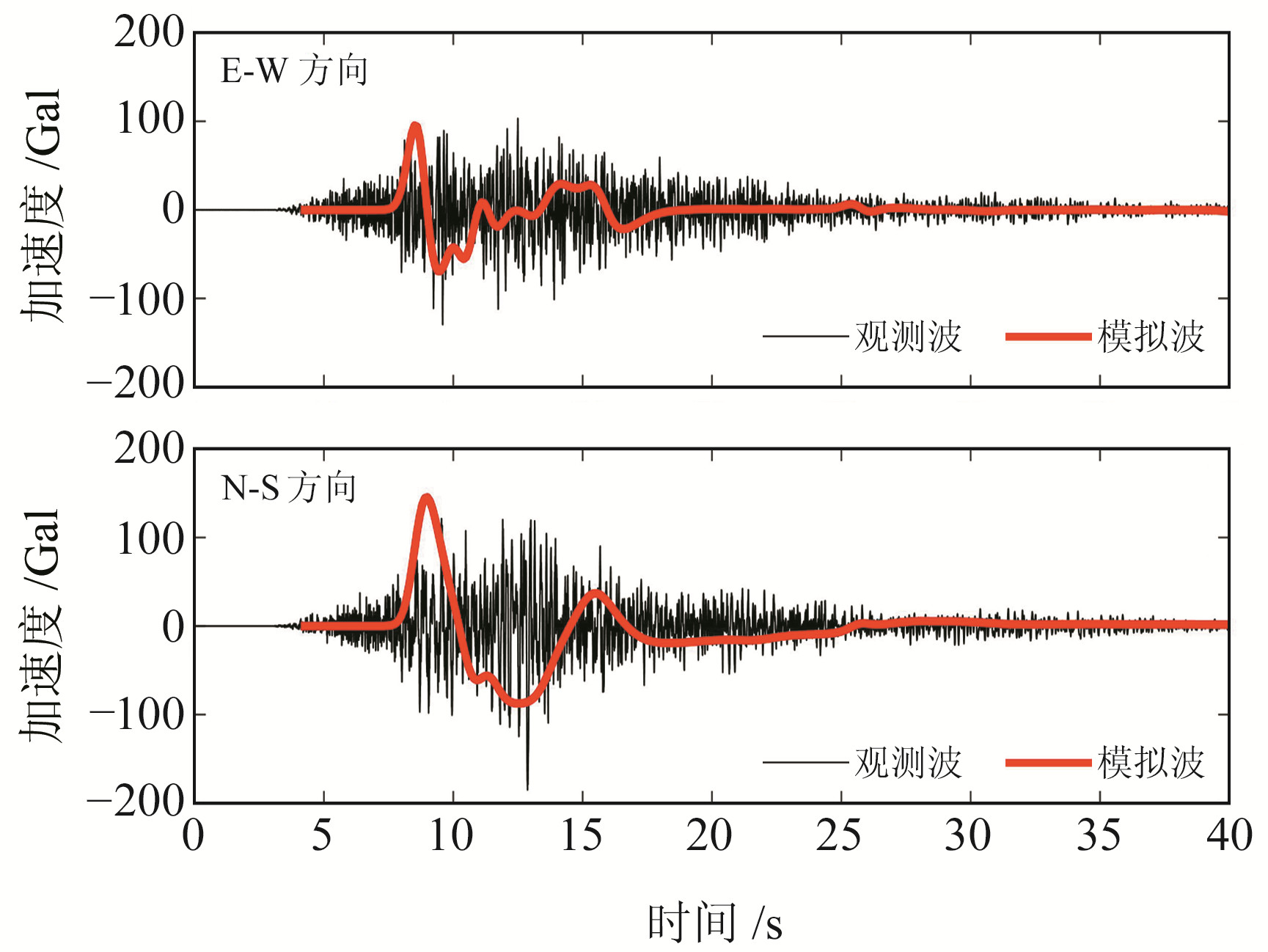
图 7为相对误差随震中距的分布情况,其中近场强震台站51JZB、51JZW和51JZY的相对误差均小于5%;随着震中距增加,相对误差呈现明显增大的趋势,可能与有限元空间分网的高频滤波效应及地震动传播过程中的介质复杂性有关。总体而言,强地面运动模拟结果的相对误差百分比整体上均小于40%,与李明会等[13]使用复合震源模型及Dang等[14]使用随机有限断层法获得的结果相当,可用于后续强地面运动场特征分析。图 8为九寨百合台(51JZB)地震动加速度观测波形与模拟波形。
|
图 7 不同台站处模拟误差随震中距的变化情况 Fig. 7 Variation of simulation error with epicenter distance at different stations |
|
图 8 51JZB台地震动加速度观测波形与模拟波形 Fig. 8 The observed and simulated waveforms of ground motion acceleration at 51JZB station |
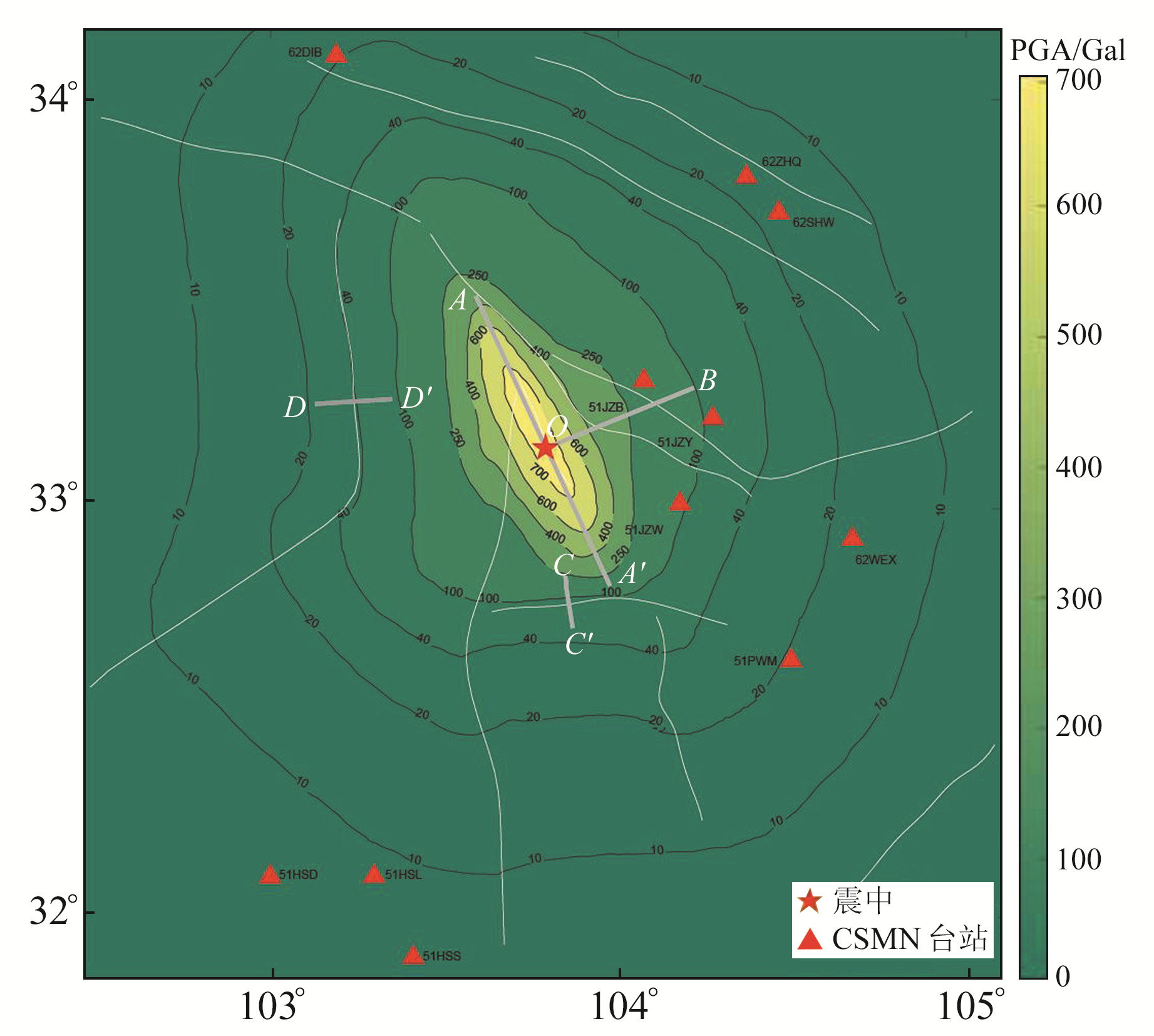
水平向地震动加速度是近场强地面运动最重要的地震动参数之一,在表征地震能量释放的同时,也是抗震设防的重要参考依据。基于二维有限元方法,本文在参数研究和不确定性分析基础上获得九寨沟M7.0地震水平向PGA空间分布。由图 9可见,近断层地区水平向PGA等值线整体呈椭圆状分布,椭圆长轴与发震断层树正断裂走向具有较好的一致性。震中附近PGA最大值约为720 Gal,且整体上随着震中距增大而不断衰减。总体而言,本文地震动峰值加速度场结果与周红[15]使用随机有限断层方法获得的结论大体一致,符合对地震动加速度分布的常规认识。值得指出的是,在PGA分布呈现出较为显著的方向效应的同时,亦呈现出断层破裂的方向效应及其与断裂带空间分布的一致性,值得进一步展开分析。
|
图 9 九寨沟地震水平向地震动峰值加速度场 Fig. 9 Horizontal peak ground acceleration field of Jiuzhaigou earthquake |
沿断裂带破裂方向的地震动幅值明显比逆破裂方向大,这种断层破裂的方向效应会使近断层地区地震动产生剧烈的空间变化。为研究九寨沟地震断层破裂的方向效应,以震中破裂起始位置为起点,计算沿破裂方向及逆破裂方向的水平向PGA。由图 10可见,2个方向的PGA均呈现出随震中距增大而衰减的特点,但随着震中距持续增大,2个方向的PGA开始呈现出差异性,沿破裂方向的PGA显著大于逆破裂方向。当震中距分别为5 km、20 km及40 km时,逆破裂方向的PGA约为沿破裂方向的96.93%、93.92%和54.24%,说明断层破裂的方向效应在近断层地区较微弱,但随着震中距增大,在远场区域更加明显。

|
图 10 近断层地区PGA的破裂方向效应 Fig. 10 Fracture directional effect of PGA in near-fault area |
建立垂直于发震断层走向的剖面,将该方向PGA与沿断层破裂方向PGA进行对比,以分析九寨沟M7.0地震的地震动方向效应。由图 11可见,随着震中距增大,2个方向的PGA均出现较为显著的衰减现象,但垂直断层方向的PGA衰减速度更快,呈现出地震动传播的方向效应。当震中距分别为5 km、20 km及40 km时,垂直断层方向的PGA约为平行断层方向的94.63%、44.02%和38.07%,说明地震动传播的方向效应在近断层地区非常显著,且随着震中距增大,在远场区域愈发明显。

|
图 11 近断层地区地震动衰减的方向效应 Fig. 11 Directional effect of ground motion attenuation in near-fault area |
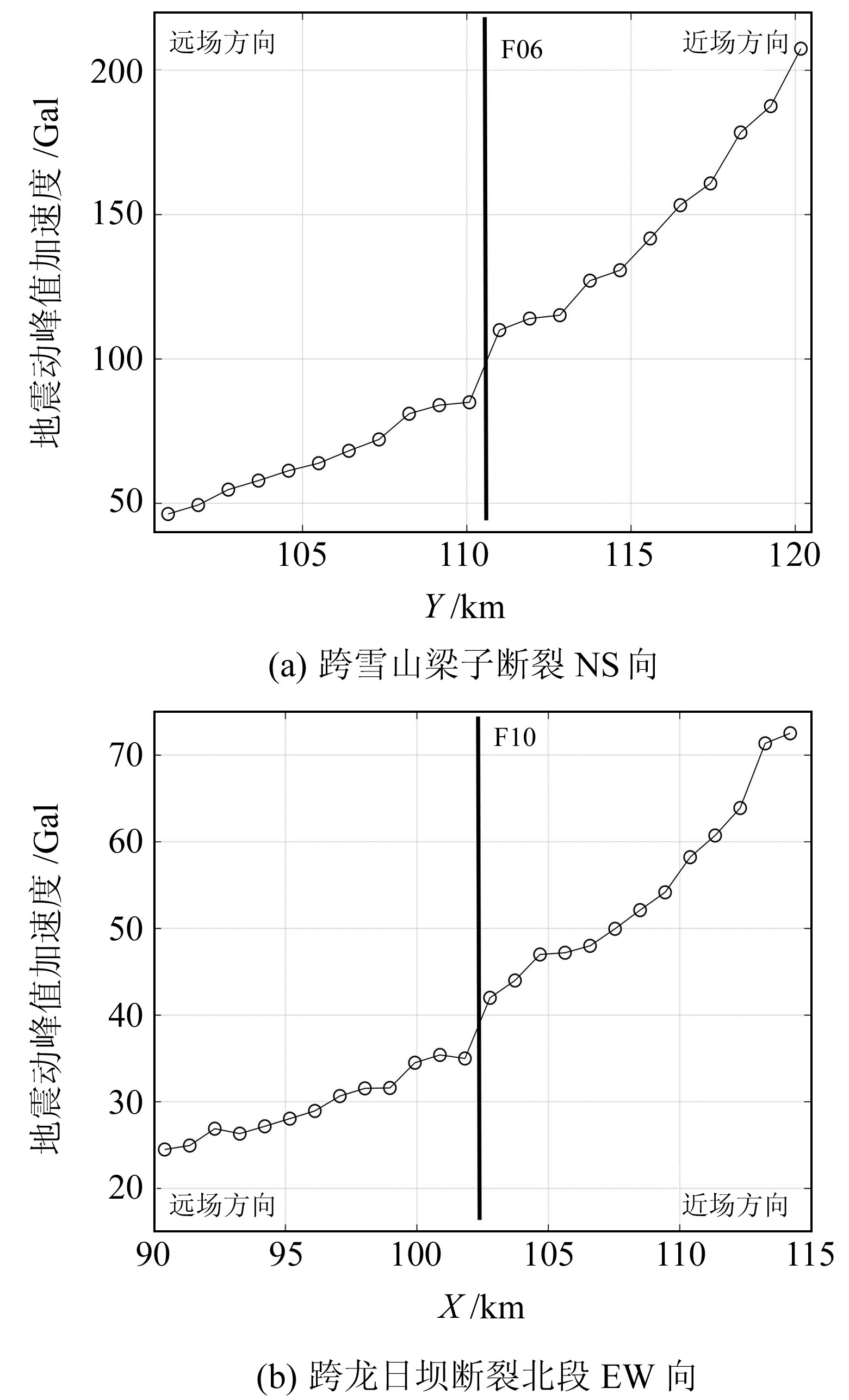
由图 2和图 9可知,水平向PGA的等值线在一定程度上与区域断裂带的空间分布一致,如雪山梁子断裂、龙日坝断裂及白龙江断裂等。为分析区域活动断裂在近场强地震动传播中的作用,建立跨雪山梁子断裂近NS向剖面C-C′及跨龙日坝断裂北段EW向剖面D-D′,图 12为2个剖面的PGA衰减情况。
|
图 12 PGA衰减 Fig. 12 PGA attenuation |
由图 12(a)可见,水平向地震动在由近场向远场传播过程中,跨雪山梁子断裂NS向PGA由110 Gal突降至85 Gal,降幅为22.72%;由图 12(b)可见,跨龙日坝断裂北段EW向PGA由42 Gal降低到35 Gal,降幅为16.67%,呈现出断裂带减震消能作用。究其成因机制,可能是断层使地震动沿断层面的透射明显降低,呈现出显著的隔震特性[16]。
4 结语基于二维有限单元法利用接触单元模拟断裂带的非连续破裂过程,建立2017-08-08四川九寨沟M7.0地震近场强地面运动估计模型,在参数研究及信度检验基础上,探讨断层破裂的方向效应、地震动传播的方向效应及其成因机理。研究结果表明:
1) 随着震源接触单元屈服应力及应力降的增大,水平向PGA整体增大,屈服应力对于强地面运动的影响更为显著;当应力降为8.5 MPa、屈服应力为4.0 MPa时,强地面运动模拟结果的相对误差百分比整体小于40%,近场强震台站的相对误差小于5%。
2) 九寨沟M7.0地震水平向PGA模拟结果等值线整体呈椭圆状,椭圆长轴与发震断层树正断裂走向具有较好的一致性;震中附近PGA最大值约为720 Gal,且整体随震中距的增大不断衰减,跨龙日坝断裂北段及跨雪山梁子断裂PGA分别降低16.67%及22.72%,这种断裂带的隔震效应或与地震动沿断层面的透射降低有关。
3) 沿断层破裂方向的PGA幅值明显大于逆断层破裂方向,呈现出较为显著的断层破裂方向效应,震中距40 km处逆断层破裂方向的PGA约为沿破裂方向的54.24%;震中距40 km处垂直断层方向的PGA约为平行断层方向的38.07%,呈现出地震动传播的方向效应。
| [1] |
Hartzell S H. Earthquake Aftershocks as Green's Functions[J]. Geophysical Research Letters, 1978, 5(1): 1-4 DOI:10.1029/GL005i001p00001
(  0) 0) |
| [2] |
王海云, 谢礼立. 近断层地震动模拟现状[J]. 地球科学进展, 2008, 23(10): 1 043-1 049 (Wang Haiyun, Xie Lili. A Review on Near-Fault Ground Motion Simulation[J]. Advances in Earth Science, 2008, 23(10): 1 043-1 049)
(  0) 0) |
| [3] |
王国新, 史家平. 经验格林函数法与随机有限断层法在合成近场强地震动中的联合运用[J]. 震灾防御技术, 2008, 3(3): 292-301 (Wang Guoxin, Shi Jiaping. The Combine Application of Empirical Green's Function and Stochastic Finite Fault Method in Simulating Near-Site Strong Ground Motion[J]. Technology for Earthquake Disaster Prevention, 2008, 3(3): 292-301 DOI:10.3969/j.issn.1673-5722.2008.03.012)
(  0) 0) |
| [4] |
Sandeep, Joshi A, Kumari P, et al. Emergence of the Semi-Empirical Technique of Strong Ground Motion Simulation: A Review[J]. Journal of the Geological Society of India, 2017, 89(6): 719-722 DOI:10.1007/s12594-017-0684-x
(  0) 0) |
| [5] |
高孟潭, 卢寿德. 关于下一代地震区划图编制原则与关键技术的初步探讨[J]. 震灾防御技术, 2006, 1(1): 1-6 (Gao Mengtan, Lu Shoude. The Discussion on Principles of Seismic Zonation of the next Generation[J]. Technology for Earthquake Disaster Prevention, 2006, 1(1): 1-6 DOI:10.3969/j.issn.1673-5722.2006.01.001)
(  0) 0) |
| [6] |
易桂喜, 龙锋, 梁明剑, 等. 2017年8月8日九寨沟M7.0地震及余震震源机制解与发震构造分析[J]. 地球物理学报, 2017, 60(10): 4 083-4 097 (Yi Guixi, Long Feng, Liang Mingjian, et al. Focal Mechanism Solutions and Seismogenic Structure of the 8 August 2017 M7.0 Jiuzhaigou Earthquake and Its Aftershocks, Northern Sichuan[J]. Chinese Journal of Geophysics, 2017, 60(10): 4 083-4 097)
(  0) 0) |
| [7] |
Goodman R E. Methods of Geological Engineering in Discontinuous Rocks[M]. New York: West Publishing Company, 1976
(  0) 0) |
| [8] |
Toki K, Miura F. Simulation of a Fault Rupture Mechanism by a Two-Dimensional Finite Element Method[J]. Journal of Physics of the Earth, 1985, 33(6): 485-511 DOI:10.4294/jpe1952.33.485
(  0) 0) |
| [9] |
Fukushima K, Kanaori Y, Miura F. Influence of Fault Process Zone on Ground Shaking of Inland Earthquakes: Verification of Mj=7.3 Western Tottori Prefecture and Mj=7.0 West off Fukuoka Prefecture Earthquakes, Southwest Japan[J]. Engineering Geology, 2010, 116(1-2): 157-165 DOI:10.1016/j.enggeo.2010.08.006
(  0) 0) |
| [10] |
徐晶, 邵志刚, 刘静, 等. 基于库仑应力变化分析巴颜喀拉地块东端的强震相互关系[J]. 地球物理学报, 2017, 60(10): 4 056-4 068 (Xu Jing, Shao Zhigang, Liu Jing, et al. Analysis of Interaction between Great Earthquakes in the Eastern Bayan Har Block Based on Changes of Coulomb Stress[J]. Chinese Journal of Geophysics, 2017, 60(10): 4 056-4 068)
(  0) 0) |
| [11] |
李宗超, 高孟潭, 陈学良, 等. 九寨沟MS7.0地震强地震动模拟及漳扎镇地震动强度预测[J]. 地球物理学报, 2019, 62(7): 2 567-2 581 (Li Zongchao, Gao Mengtan, Chen Xueliang, et al. Simulation of Ground Motion by the 2017 Jiuzhaigou MS7.0 Earthquake and Estimation of Ground Motion Intensity in the Zhangzha Town[J]. Chinese Journal of Geophysics, 2019, 62(7): 2 567-2 581)
(  0) 0) |
| [12] |
王德才, 何骁慧. 地震动模拟过程中断层参数的敏感性分析[J]. 地震工程学报, 2016, 38(2): 212-218 (Wang Decai, He Xiaohui. Sensitivity Analysis of Fault Parameters during Ground Motion Simulation[J]. China Earthquake Engineering Journal, 2016, 38(2): 212-218)
(  0) 0) |
| [13] |
李明会, 景月岭, 张宇璇, 等. 九寨沟MS7.0地震强地震动模拟及参数敏感性分析[J]. 大地测量与地球动力学, 2022, 42(10): 1 025-1 033 (Li Minghui, Jing Yueling, Zhang Yuxuan, et al. Strong Ground Motion Simulation and Parameter Sensitivity Analysis of the Jiuzhaigou MS7.0 Earthquake[J]. Journal of Geodesy and Geodynamics, 2022, 42(10): 1 025-1 033)
(  0) 0) |
| [14] |
Dang P F, Liu Q F, Song J. Simulation of the Jiuzhaigou, China, Earthquake by Stochastic Finite-Fault Method Based on Variable Stress Drop[J]. Natural Hazards, 2020, 103(2): 2 295-2 321
(  0) 0) |
| [15] |
周红. 基于NNSIM随机有限断层法的7.0级九寨沟地震强地面运动场重建[J]. 地球物理学报, 2018, 61(5): 2 111-2 121 (Zhou Hong. Reconstruction of Strong Ground Motion of Jiuzhaigou M7.0 Earthquake Based on NNSIM Stochastic Finite Fault Method[J]. Chinese Journal of Geophysics, 2018, 61(5): 2 111-2 121)
(  0) 0) |
| [16] |
谭云亮, 谭涛, 张修峰, 等. 正断层两盘动力灾害显现差异性及机制[J]. 煤炭科学技术, 2023, 51(1): 214-223 (Tan Yunliang, Tan Tao, Zhang Xiufeng, et al. Difference and Mechanism of Dynamic Behaviors between Two Walls of Normal Fault[J]. Coal Science and Technology, 2023, 51(1): 214-223)
(  0) 0) |
2. School of Civil, Architecture and Environment, Hubei University of Technology, 28 Nanli Road, Wuhan 430068, China
 2023, Vol. 43
2023, Vol. 43


