随着正演计算方法的发展和计算机性能的提高,神经网络为地球物理学研究打开了新的篇章。已有研究表明,神经网络在电磁反演中具有可行性[1-2],但目前大部分神经网络在可控源电磁反演中的应用是基于反向传播等传统方法提供初始输入的一次性生成的网络模型。神经网络的非线性优势在分类问题上效果显著,但在回归预测方面其优势会弱化,导致神经网络模型出现过拟合或欠拟合等问题[3]。在神经网络训练中,较少的特征无法很好地反映地表特征场源之间的关系,因此一般使用高维的训练样本,但这也容易导致网络模型不收敛[4]。由此可见,神经网络在可控源电磁法中的应用具有一定的挑战性,同时也有很大的科研拓展空间。
本文提出一种卷积神经网络(convolutional neural network,CNN)和生成对抗网络(generative adversarial networks,GAN)相结合的CNN-GAN组合模型来解决可控源电磁二维反演问题。CNN具有较强的空间提取能力,而GAN判别器的识别能力可以增强网络,抓取更多的数据信息。使用CNN从差分总场中提取地下异常体电导率的空间数据信息,再将获得的数据信息输入GAN,以改进数据图像重建。通过CNN-GAN组合模型训练方法可以使网络拥有更强的学习能力,更加有效地挖掘输入与标签之间数据的关联性,最后利用直方图交互法将组合模型的预测结果与传统网络模型的预测结果进行对比。
1 方法原理地电模型由空气层、地层和地下异常体3部分组成,接收区域位于地面,异常体位于地下,磁偶极子发射源位于异常体上方,其横坐标位于原点处,地电模型如图 1所示。

|
图 1 地电模型示意图 Fig. 1 Schematic diagram of geoelectric model |
根据麦克斯韦方程组和相应的电磁张量格林函数,可以写出任意电流分布为j(r)的电场公式:
| $ E\left(r_j\right)=\iiint_D \hat{G}_E\left(r_j \mid r\right) \cdot j(r) \mathrm{d} v=G_E(j(r)) $ | (1) |
式中,rj为剖分后的任意点,E为电场,GE为电场格林算子,D为异常体内部区域。
将背景介质的过载电流
| $ \left\{\begin{array}{l} \nabla \times H=\tilde{\sigma}_b E+j^a+j^e \\ \nabla \times E=i \omega \mu_0 H \end{array}\right. $ | (2) |
式中,ω为角频率,μ0为真空中的磁导率,je为外部电流密度,
| $ E\left(r_j\right)=G_E\left(j^a\right)+G_E\left(j^e\right) $ | (3) |
式中,GE(ja)为过载电流ja产生的异常场,GE(je)为对应背景介质的外部电流je产生的背景场。另有:
| $ E^a\left(r_j\right)=G_E\left(j^a\right)=G_E(\tilde{\sigma} E) $ | (4) |
| $ E^b\left(r_j\right)=G_E\left(j^e\right) $ | (5) |
式中,Ea为由模型中异常体电导率
| $ E\left(r_j\right)=G_E(\tilde{\sigma} E)+E^b\left(r_j\right) $ | (6) |
若已知非均匀区域内的电场和异常体电导率,使用式(6)便可求出任意点rj的电场[5]。式(6)为电磁正演模拟建立了基础。
由于异常体位于地下深处,异常场相比于背景场弱,电磁场数据信息容易受噪声干扰,为有效减弱背景场的影响,引入差分总场模拟方法对输入数据进行预处理。在建立正演模型时,将磁偶极子发射源A和磁偶极子发射源B分别放置于异常体上、下方,求总场差值,从而提高异常场精度并减小噪声影响,提高输入数据质量。差分总场ΔE与异常体电导率
| $ \begin{gathered} \Delta E=E_1\left(r_j\right)-E_2\left(r_j\right)=G_{E_1}\left(\tilde{\sigma} E_1\right)+ \\ E_1^b\left(r_j\right)-G_{E_2}\left(\tilde{\sigma} E_2\right)+E_2^b\left(r_j\right) \end{gathered} $ | (7) |
式中,E1和E1b分别为发射源A的总场和背景场,E2和E2b则分别为发射源B的总场和背景场。
2 CNN-GAN组合模型原理 2.1 卷积神经网络卷积神经网络(CNN)是深度学习中的代表网络之一,由输入层、输出层、全连接层、卷积层和池化层5部分组成,具体的网络结构[6]如图 2所示。由于CNN可以将模型中的特征提取出来,然后根据模型的特征进行识别、分类或预测等,其在地震及电磁数据分析领域中的应用十分广泛。

|
图 2 CNN示意图 Fig. 2 Schematic diagram of CNN |
CNN主要通过训练网络来学习输入与输出之间的关系,而在其应用于地球物理领域时,可以把某点观测的电磁场数据看成一个特征。因此,本文将地面接收机接收及处理后的差分总场作为该网络模型的输入,将地下异常体的电导率作为输出,通过一系列卷积操作有效提取出输入和输出数据之间的映射关系。将ADAM优化器应用于CNN中,该优化器将AdaGrad算法和RMSProp算法的优点相结合,可对网络中的每个参数使用相同学习率,并独立适应神经网络的学习[7]。
虽然CNN可实现地下异常体电导率的粗略重构,但其池化层丢失了一些有价值的信息,忽略了局部与整体之间的关系,导致精度较低,不能满足工程应用的要求。因此,本文将CNN的训练过程作为传统深度学习方法的初值选择过程,再使用GAN对模型进行优化。
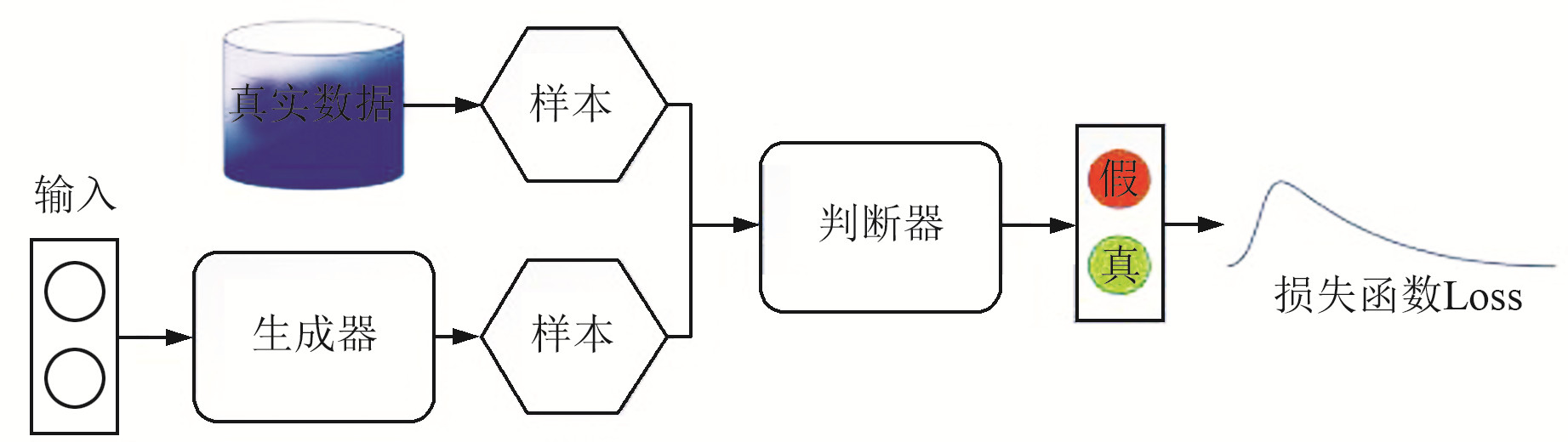
2.2 生成对抗网络生成对抗网络(GAN)由生成器和判别器两部分组成,具体结构如图 3所示。与CNN不同,GAN是基于模拟人脑建模的,需要不断学习和模仿,以提升到与标签数据一致且符合需要的建模水平[8]。
|
图 3 GAN示意图 Fig. 3 Schematic diagram of GAN |
在传统GAN中,常使用随机噪声作为生成器的输入,但噪声是随机采样的,并且噪声在原始空间的映射并不是满射的,这是导致GAN崩溃的原因之一。所以,本文直接使用CNN的输出作为GAN生成器的输入,同时也使用ADAM优化器优化二元交叉熵更新生成器的权重。
2.3 评价指标 2.3.1 CNN的评价指标均方根误差(RMSE)是判断CNN预测效果的指标之一。RMSE擅长追踪异常的数据值,注重预测结果中异常值对模型效果的影响,RMSE值越小,其训练效果越好[9]。RMSE的计算公式为:
| $ \mathrm{RMSE}=\sqrt{\frac{1}{m} \sum\limits_{i=1}^m\left(Y_i-f\left(x_i\right)\right)^2} $ | (8) |
式中,m为样本总数,Yi为预测的地下异常体电导率,f(xi)为真实的地下异常体电导率。
2.3.2 GAN的评价指标传统GAN的损失函数常表示为:
| $ \begin{gathered} \min _G \max _D V(D, G)=E_{x \sim P_{\text {data }}}[\log D(x)]+ \\ E_{z \sim P_z}[\log (1-D(G(z))] \end{gathered} $ | (9) |
式中,G为生成器,D为判别器,V(D, G)为其运算关系,x为真实数据,Z为噪声数据,E为数学期望,Pdata为真实数据的分布,Pz为噪声数据的分布,G(z)为生成器生成样本的数据,D(x)为判别器判别图片的真实概率。
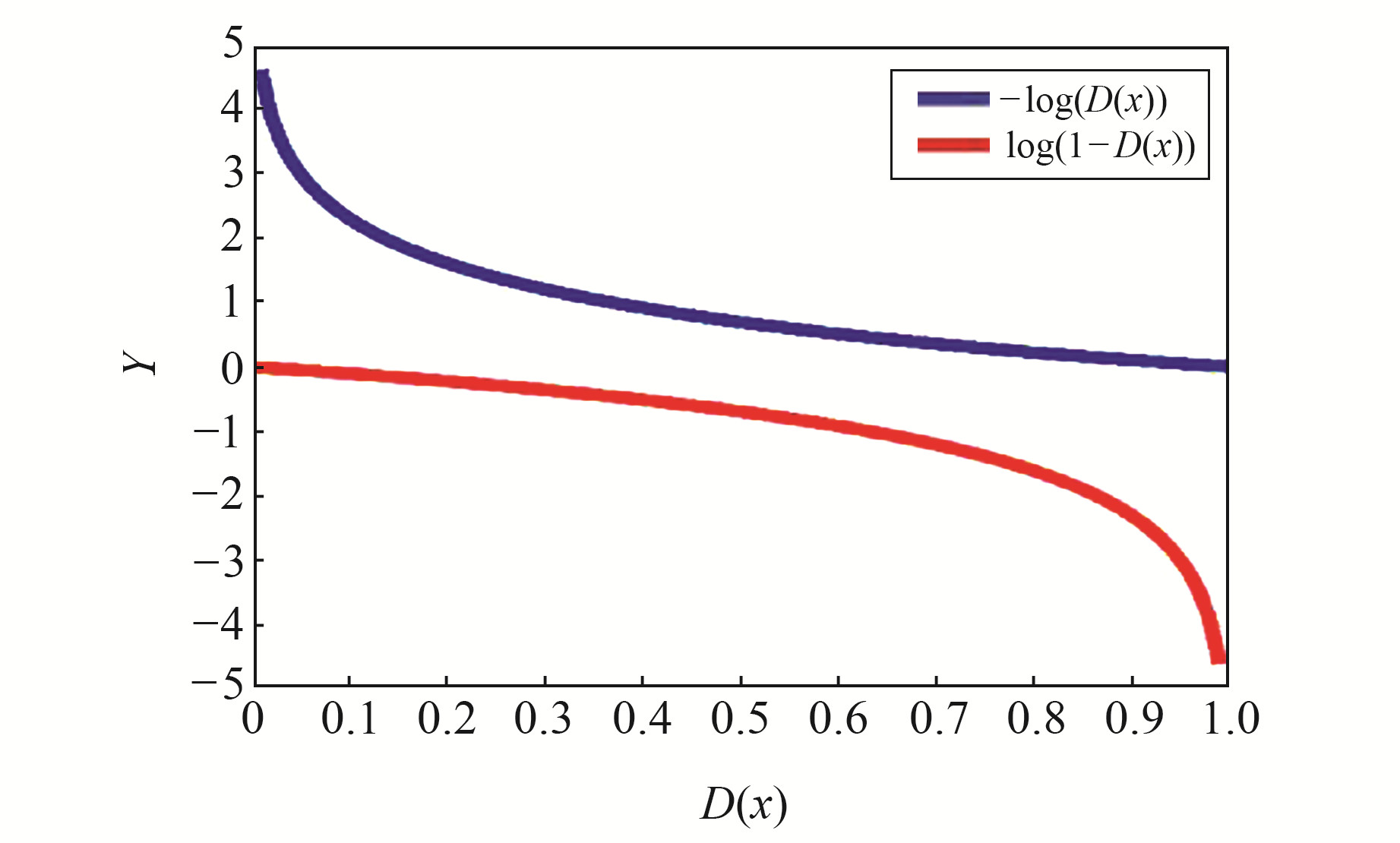
传统GAN的损失函数常用log(1-D(G(z)))表示生成器的交叉熵,但通过图 4中log(1-D(x))函数曲线发现,当D(x)接近0时,梯度非常小。所以,在传统GAN训练初期,生成器“欺骗”判别器的效率很低。虽然-log(D(x))函数和log(1-D(x))函数的整体趋势都是递减的,但-log(D(x))函数在D(x)接近0时梯度较大,有利于提高生成器在训练初期“欺骗”判别器的效率,从而提高GAN整体的训练速度。此外,为尽可能增强生成器的性能,避免训练模型出现过拟合的现象,本文增加了L1正则化(L1 regularization)作为损失函数的惩罚项[10],因此可将生成器的损失函数Loss(G)表示为:
| $ \begin{gathered} \operatorname{Loss}(G)=-\frac{1}{m} \sum\limits_{i=1}^m \log (D(G(z))) \times \\ W_G+\frac{1}{m} \sum\limits_{i=1}^m|D(x)-D(G(z))| \times W_{\mathrm{L} 1} \end{gathered} $ | (10) |
|
图 4 两种log函数对比 Fig. 4 Comparative diagram of the twolog functions |
式中,m为样本个数,WG为GAN生成器损失的权重初始值,WL1为平均绝对误差的权重初始值。
对于GAN的判别器损失函数Loss(D)可表示为:
| $ \begin{gathered} \operatorname{Loss}(D)=\frac{1}{m} \sum\limits_{i=1}^m- \\ {[\log (D(x)+\beta)+\log (1-D(G(z))+\beta)]} \end{gathered} $ | (11) |
式中,β为常数,用于确保log函数里面的参数大于0。
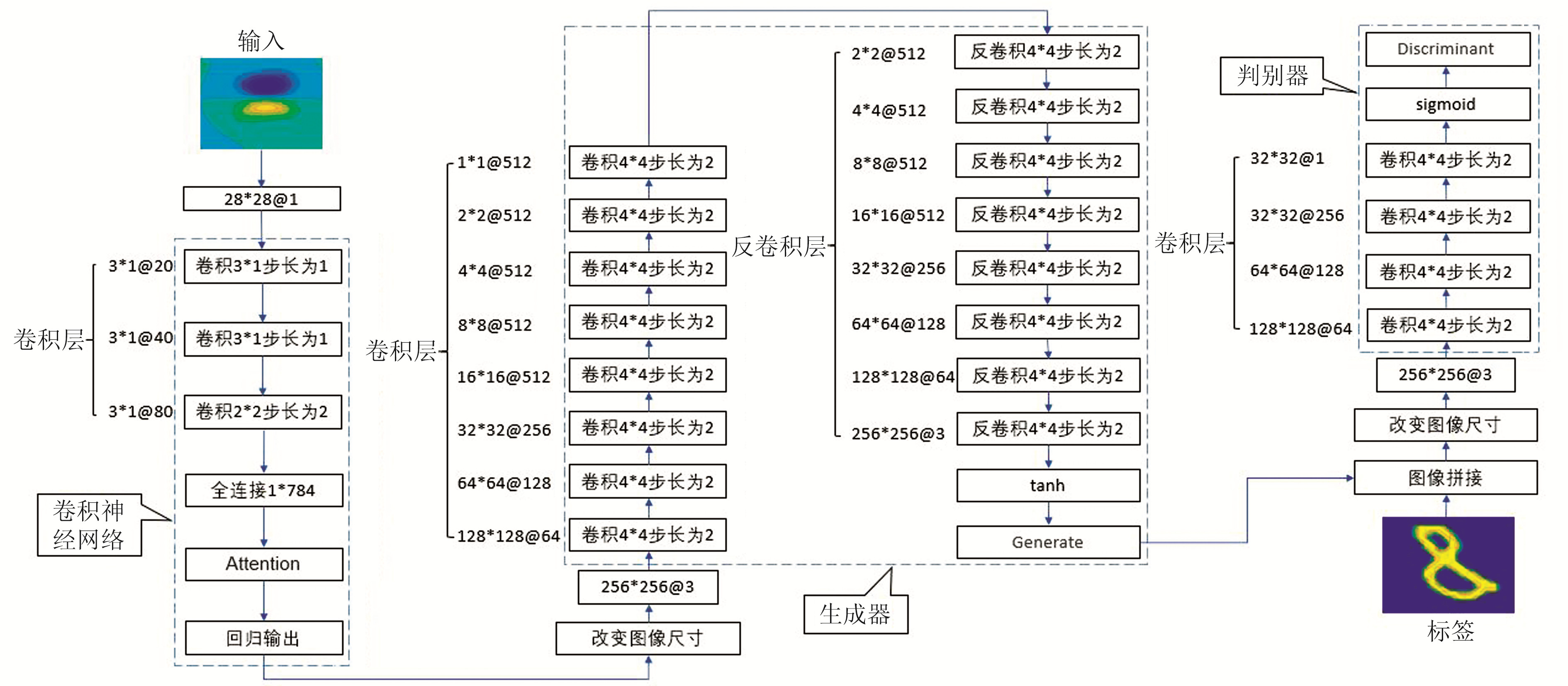
2.4 CNN-GAN组合模型本文提出的CNN-GAN组合模型结构如图 5所示,该模型弥补了单一网络容易出现训练效果不稳定的缺点。考虑到现实情况中获取差分总场相位的成本很高,所以将差分总场以幅值的形式作为输入。差分总场幅值可表示为:
| $ M=\sqrt{\operatorname{Re}^2+\operatorname{Im}^2} $ | (12) |
|
图 5 CNN-GAN组合模型 Fig. 5 CNN-GAN combinatorial model |
式中,M为差分总场幅值,Re为差分总场实部的模值,Im为差分总场虚部的模值。通过CNN初步完成对地下异常体电导率的粗略预测,再将预测结果送入GAN生成器中,然后将生成器的预测结果与真实数据信息一同传入到判别器中,判别器将判断结果反馈给生成器,通过生成器和判别器相互对抗,提高生成器的回归预测能力,充分挖掘出差分总场中的隐藏信息。
3 实验及结果分析 3.1 模型建立与实验参数本文使用电磁仿真模拟软件批量制作以差分电场幅值作为输入和以异常体电导率模型作为输出的数据集。该软件是基于积分方程方法的频率域建模软件,可设计三维地电结构模型,并实现平面波水平和垂直方向的双极源及X、Y、Z三方向的场源模拟,通过修改参数文件来实现地电模型的模拟,参数设置包括场源参数、激发频率、层状模型参数、异常体剖分及异常体电导率等,运行程序即可获得相应的电磁场数据。
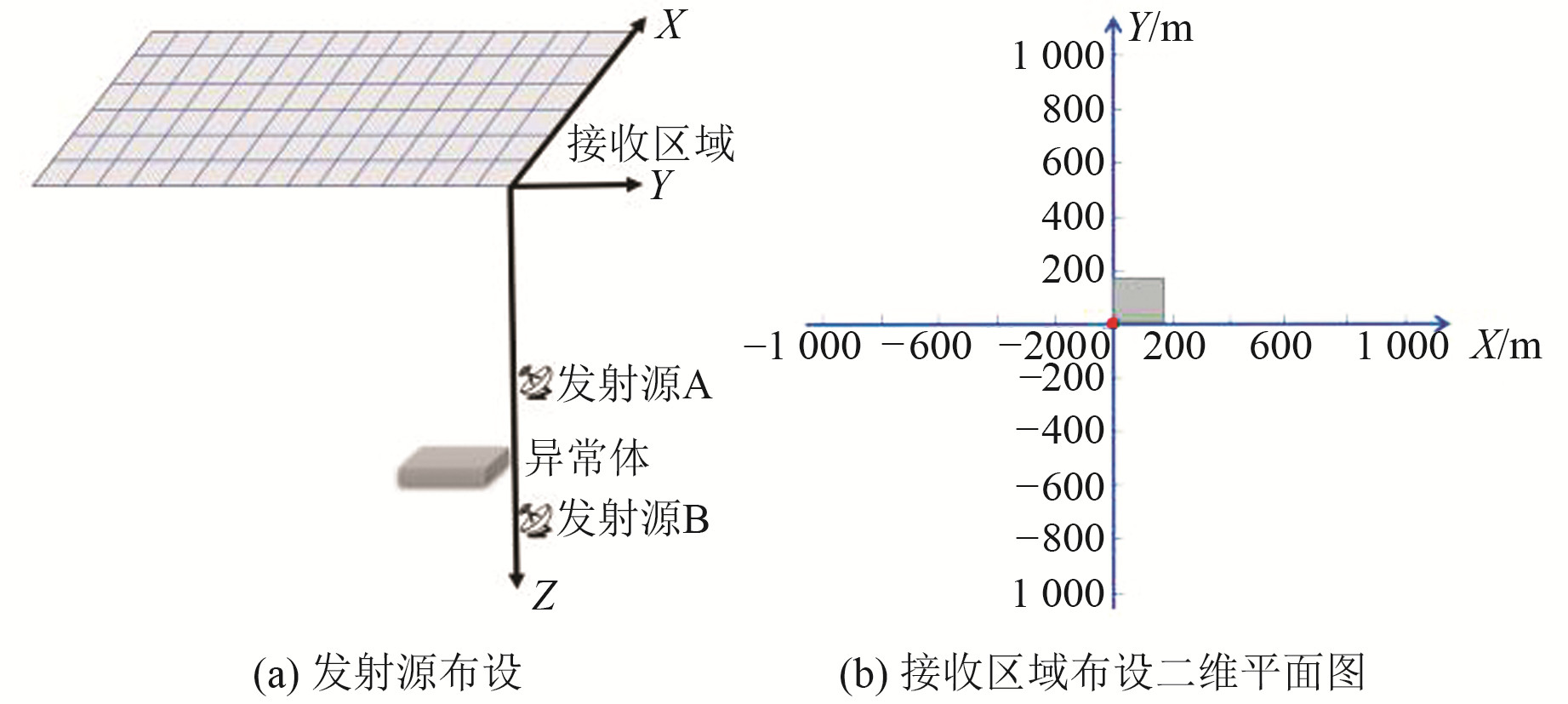
根据油田实际情况建立地电模型,地下异常体的范围为140 m×140 m×8 m,剖分网格大小为28 m×28 m×2 m,地下异常体形态与电导率是基于MNIST手写数字集随机生成的,且异常体电导率经过归一化的数据预处理后在0~1之间随机变化。如图 6(a)所示,接收区域在地面上2 000 m×2 000 m,异常体位于地下1 400 m,频率设置为200 Hz。以磁偶极子发射源为中心布设接收区域,在已知异常体所在储层大致位置的情况下,发射源A和发射源B分别位于异常体上方和下方100 m处,坐标分别为(0 m,0 m,1 308 m)、(0 m,0 m,1508 m),异常体坐标范围为X(0~140 m)、Y(0~140 m)、Z(1 400~1 408 m),接收区域范围为X(-1 000~1 000 m)、Y(-1 000~1 000 m)。接收区域布设如图 6(b)所示,其中红点为发射源的位置,灰色矩形为异常体。
|
图 6 可控源模型示意图 Fig. 6 Schematic diagram of controllable source model |
CNN-GAN组合模型的硬件环境包括AMD Ryzen 7 5800H with Radeon Graphics@3.20 GHz,NVIDIA GeForce RTX 3050Ti Laptop GPU;软件环境包括Python 3.5,TensorFlow1.2和CUDA 10.2等。其中,CNN的学习率设置为0.001,GAN中生成器和判别器的学习率分别设置为0.002和0.000 01,训练的批量大小为1,Epoch设置为120,初始权重WG和WL1分别设置为1.0和0.1。
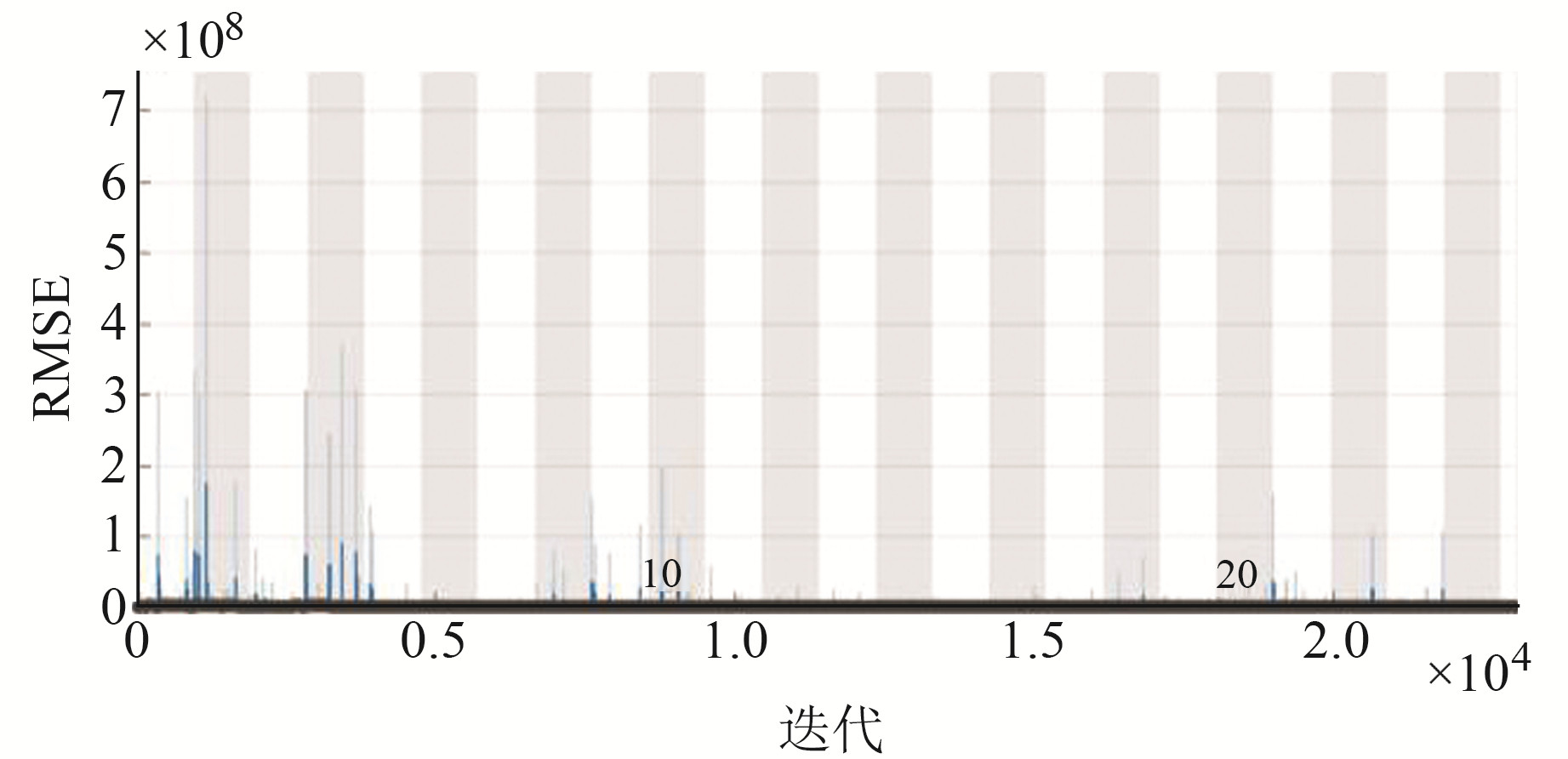
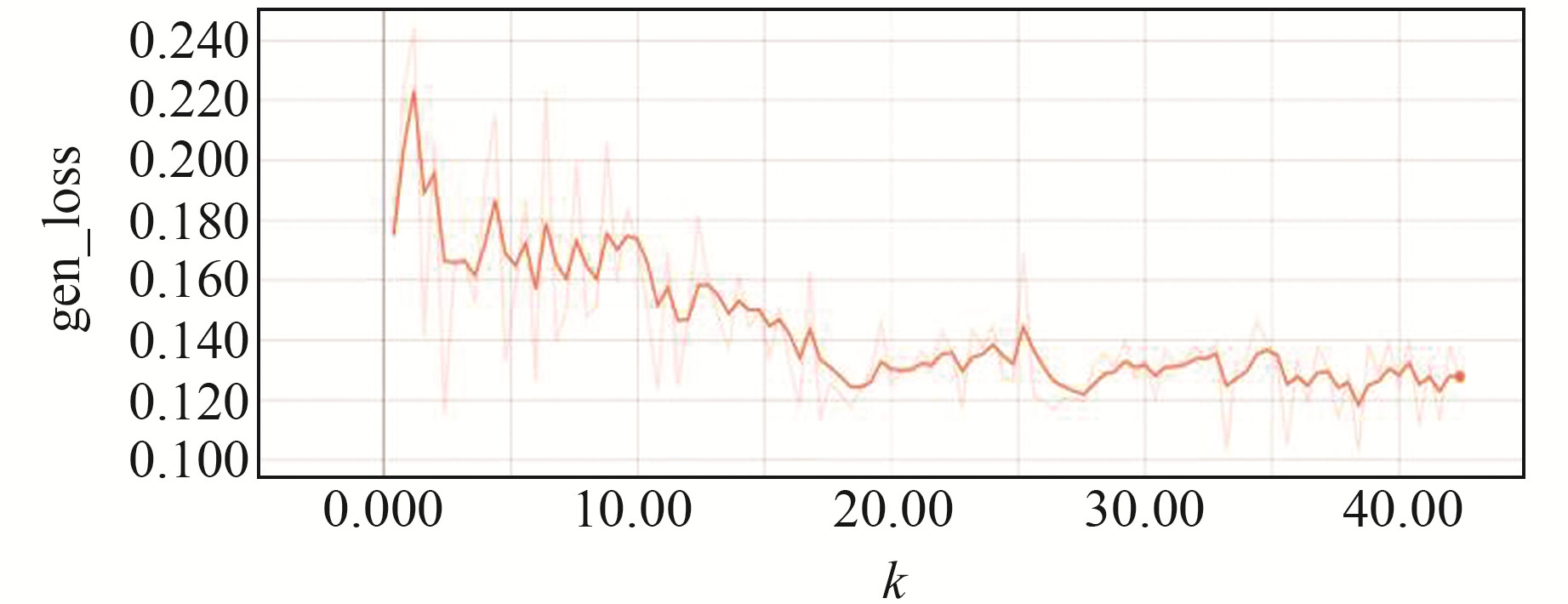
3.2 结果与分析数据集由地面接收器采集到的作为深度学习网络输入的差分总场幅值和作为网络输出的地下异常体电导率构成。随着网络模型学习参数的增加,训练所需数据也会增加,所以高质量的数据更能对网络性能产生积极影响[11]。经测试,选取1 000个数据集相较于500个数据集对于网络性能有较大提升;而选取1 200个数据集和1 500个数据集相较于1 000个数据集对于网络性能的提升并不显著。因此,考虑到计算效率和时间成本,本文挑选了1 000个异常体占比较大的高质量数据集作为训练样本,200个数据集作为测试样本,送入CNN进行训练,并使用均方根误差(RMSE)作为衡量指标。由图 7可以看出,曲线呈跳跃状,训练过程不稳定,只能给出粗略的预测结果。再将CNN中粗略的预测结果送入GAN,结果如图 8所示,随着训练次数的增加,生成器的损失函数也逐渐降低,前150次迭代GAN生成器和判别器处于激烈的对抗训练中,迭代至18 000次后趋于平稳,模型基本收敛,结果达到预期效果。由此可知,CNN-GAN组合模型训练花费时间为36 783 s。
|
图 7 CNN网络的均方根误差 Fig. 7 RMSE of CNN |
|
图 8 生成器损失函数 Fig. 8 Generator loss function |
分别使用CNN、GAN及CNN-GAN组合模型进行对比实验,结果如图 9所示。可以看出,CNN及GAN只能粗略预测异常体电导率,而CNN-GAN组合模型预测的电导率分布与真实情况基本一致,可精确反演出地下异常体的位置形状。

|
(a)差分总场幅值作为神经网络的输人; (b)真实异常体电导率分布作为神经网络的标签; (c)基于CNN的二维反演异常体电导率分布; (d)基于GAN的二维反演异常体电导率分布; (e)基于CNN-GAN的二维反演异常体电导率分布 图 9 不同网络模型预测的电导率对比 Fig. 9 Comparative plot of conductivity predicted by different network models |
本文采用直方图相交法计算模型输出和标签之间的相似度,将彩色图分为3个通道并绘制直方图[12],将CNN、GAN及CNN-GAN组合模型预测图形的直方图分别与标签RGB三通道直方图进行匹配,并对匹配结果求平均值,分别得出不同网络模型预测的图形与标签的相似度(表 1),发现CNN-GAN组合模型预测的电导率与标签相似度高达94.38%。
|
|
表 1 不同模型预测图形的相似度 Tab. 1 Similarity of graphs predicted by different models |
针对传统可控源电磁反演方法容易陷入局部最小、计算量大及反演结果不稳定等问题,本文提出一种基于CNN和GAN的组合神经网络模型。该模型不仅在总场数据送入网络前对其进行差分预处理,还提高了CNN的提取能力及GAN的稳定性。将CNN-GAN组合模型的预测结果与传统CNN和GAN的预测结果进行分析对比,结果显示,CNN-GAN组合模型预测效果最好,相似度高达94.38%,比传统CNN和GAN模型分别提高约48%、78%。
神经网络模型在可控源反演领域还存在许多问题,后期将提高模型的训练效率,改善CNN-GAN组合模型的泛化能力,以提高其实用性。
| [1] |
Carbonari R, Di Maio R, Piegari E, et al. Filtering of Noisy Magnetotelluric Signals by SOM Neural Networks[J]. Physics of the Earth and Planetary Interiors, 2018, 285: 12-22 DOI:10.1016/j.pepi.2018.10.004
(  0) 0) |
| [2] |
王鹤, 刘梦琳, 席振铢, 等. 基于遗传神经网络的大地电磁反演[J]. 地球物理学报, 2018, 61(4): 1 563-1 575 (Wang He, Liu Menglin, Xi Zhenzhu, et al. Magnetotelluric Inversion Based on BP Neural Network Optimized by Genetic Algorithm[J]. Chinese Journal of Geophysics, 2018, 61(4): 1 563-1 575)
(  0) 0) |
| [3] |
Belkebir K, Chaumet P C, Sentenac A. Superresolution in Total Internal Reflection Tomography[J]. Journal of the Optical Society of America A, Optics, Image Science, and Vision, 2005, 22(9): 1 889-1 897 DOI:10.1364/JOSAA.22.001889
(  0) 0) |
| [4] |
刘彦锋, 张文彪, 段太忠, 等. 深度学习油气藏地质建模研究进展[J]. 地质科技通报, 2021, 40(4): 235-241 (Liu Yanfeng, Zhang Wenbiao, Duan Taizhong, et al. Progress of Deep Learning in Oil and Gas Reservoir Geological Modeling[J]. Bulletin of Geological Science and Technology, 2021, 40(4): 235-241)
(  0) 0) |
| [5] |
Raiche A P. An Integral Equation Approach to Three-Dimensional Modelling[J]. Geophysical Journal International, 1974, 36(2): 363-376 DOI:10.1111/j.1365-246X.1974.tb03645.x
(  0) 0) |
| [6] |
Szegedy C, Vanhoucke V, Ioffe S, et al. Rethinking the Inception Architecture for Computer Vision[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Las Vegas, USA, 2016
(  0) 0) |
| [7] |
Kingma D P, Ba J. Adam: A Method for Stochastic Optimization[C]. 3rd International Conference on Learning Representations, La Jolla, 2015
(  0) 0) |
| [8] |
Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Networks[J]. Communications of the ACM, 2020, 63(11): 139-144 DOI:10.1145/3422622
(  0) 0) |
| [9] |
Yang Z P, Lu W X, Long Y Q, et al. Application of Back-Propagation Artificial Neural Network Models for Prediction of Groundwater Levels: Case Study in Western Jilin Province, China[C]. 2008 2nd International Conference on Bioinformatics and Biomedical Engineering, Shanghai, 2008
(  0) 0) |
| [10] |
Zhang Y C, Song L, Xie R, et al. Multi-Scale Generative Adversarial Learning for Facial Attribute Transfer[M]. Singapore: Springer Singapore, 2020
(  0) 0) |
| [11] |
李卫. 深度学习在图像识别中的研究及应用[D]. 武汉: 武汉理工大学, 2014 (Li Wei. The research and application of deep learning in image recognition[D]. Wuhan: Wuhan University of Technology, 2014)
(  0) 0) |
| [12] |
Sonka M, Hlavac V, Boyle R. 艾海舟, 苏延超, 译. 图象处理、分析与机器视觉[M]. 北京: 人民邮电出版社, 2002 (Sonka M, Hlavac V, Boyle R. Ai Haizhou, Su Yanchao, Translate. Image Processing, Analysis, and Machine Vision[M]. Beijing: Posts and Telecom Press, 2002)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


