板块俯冲是地壳向地幔进行物质和能量传输的重要方式之一,也是地壳缩短、消亡的主要因素[1-2]。长期的板块俯冲作用会沿着俯冲界面产生应力积累,并在震空区逐渐增加,当应力超过岩层承受强度时,则会以地震、海啸、火山喷发等形式释放,给人类生命财产安全带来损失[3]。
厘清巨型逆冲断裂闭锁特征与地表形变的关系,是理解俯冲带地震周期模式的关键环节[4]。根据现代大地测量资料,反演断裂面闭锁程度和滑动亏损分布特征是评估断裂带未来地震危险性的重要手段[5]。研究表明,在震间深部蠕滑区,俯冲板块的推挤作用会引发软流层缓慢的粘性流动,从而导致地表速度场发生显著变化,并展现出更远距离的长波形变模式,即震间深部粘弹性圈层的动力效应,会在一定程度上影响地表变形[4, 6-8]。然而,目前基于Okada弹性半空间的位错理论在推估断层闭锁特征时往往会忽略板块粘弹性变形随时间的变化特征,存在一定局限性[9-11]。同时为拟合GPS实测形变场,弹性模型可能会在一定程度上将断层的闭锁区域估算得更深,从而导致区域闭锁特征估计错误[8, 12]。因此,基于考虑深部介质差异的粘弹性模型来重新评估俯冲区的闭锁深度十分重要。
研究断裂的震间闭锁深度能够有效判断断层应力积累特征,对于评估区域未来地震危险性和研究岩石圈流变特性都具有重要意义[13-16]。前人针对厄瓜多尔俯冲区的研究大多基于弹性回跳理论来反演断层闭锁特征,鲜有从粘弹性模型角度出发,并基于数值模拟的方法研究该区域的断层闭锁分布[17]。基于此,本文以该区较为密集的GPS速度场为约束,分别建立厄瓜多尔俯冲区纯弹性与弹性+粘弹性的地球模型,并采用有限元数值模拟方法,研究深部粘弹性圈层对震间地表变形的响应特征,从而对俯冲区的闭锁深度重新进行评估。
1 地质背景南美板块位于纳斯卡板块、可可斯板块与大西洋板块之间,受到来自纳斯卡板块东向强烈冲击和大西洋海底拉张应力,导致板内形变非常复杂[13, 18]。
本文研究区位于纳斯卡板块和南美板块俯冲区北部,主要包括厄瓜多尔与哥伦比亚南部,也称厄瓜多尔俯冲区,西侧的纳斯卡板块以约55 mm/a的速度沿N83°E方向俯冲至厄瓜多尔的南美板块之下[16]。大地测量数据表明,在厄瓜多尔北部,Rio-Chingual-La-Sofia断层存在约7.6±0.5 mm/a的右旋运动;而中部Pallatanga断层右旋运动减少到5.3±0.4 mm/a;南部则几乎无应变积累,GNSS速度降至约3 mm/a,并转向东南方向[1, 17, 19]。由此可知,厄瓜多尔地区地壳运动的主要动力来源于纳斯卡板块和南美板块之间的俯冲碰撞。此外,在厄瓜多尔南部,位于纳斯卡板块之上的卡内基海脊与南美洲大陆发生次生碰撞,导致局部构造变形极为复杂[20]。为简化模型,本文在之后研究中并未考虑卡内基海脊对南美大陆的碰撞变形作用。
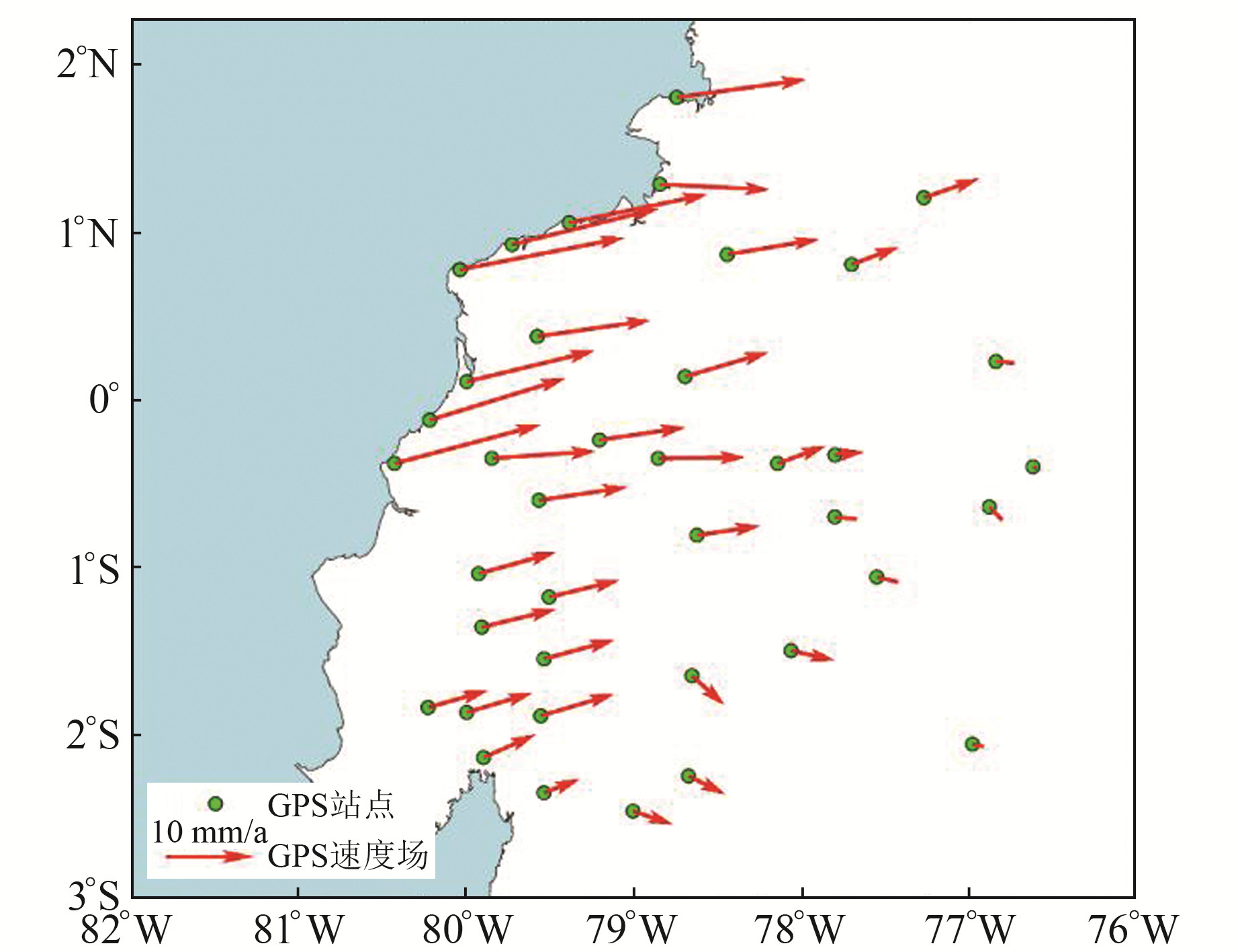
2 数据和方法 2.1 GPS速度场Mocquet等[11]采用GAMIT/GLOBK软件和地球动力学的标准策略,获取了1994~2012年GPS时间序列,在分析所有GPS站点速度时考虑GPS时间序列中与时间相关的噪声。本文采用的GPS速度场来自该研究中相对稳定的南美洲大陆水平速度场(图 1),区域速度场图像表明,南美板块整体呈东向运动,并沿内陆方向运动速率逐渐降低。
|
图 1 厄瓜多尔地区GPS水平速度场 Fig. 1 GPS horizontal velocity field in Ecuador region |
由于卡内基海脊海沟对厄瓜多尔南部存在碰撞作用,导致邻区GPS数据出现明显的离群现象。为简化模型,本文并未顾及海脊的作用机制,因此剔除该区域部分GPS站点,重点考虑纳斯卡俯冲板块对南美大陆的俯冲作用,最终选取的GPS站点如图 1所示。
2.2 有限元模型为厘清震间地表形变与深部粘弹性圈层的响应机制,本文分别建立纯弹性模型与弹性地壳+粘弹性软流圈模型。其中,有限元模型主要考虑海洋板块和大陆板块,在板块上方被定义为延伸至各自估计弹性厚度的纯弹性体,分别为大陆地壳和海洋地壳;在板块下方则认为岩石圈和软流圈地幔为各向同性的大陆地幔域和海洋地幔域,这些地幔域在弹性模型中具有纯弹性性质,而在粘弹性模型中则具有粘弹性性质[8]。本文建立的三维粘弹性有限元模型可分为4个块体,分别为海洋地壳、陆地地壳、海洋地幔和陆地地幔(图 2(a)),模型几何构建与地壳厚度主要来自crust1.0(https://igppweb.ucsd.edu/) 与部分前期研究成果[10, 17, 21]。由于莫霍面的复杂性,本文对所建模型进行一定程度的简化处理,将海洋地壳与陆地地壳厚度均设置为30 km,该深度以下为粘弹性地幔区域[8]。

|
图 2 研究区有限元模型示意图 Fig. 2 Schematic diagram of thefinite element model of the study area |
在建立的三维有限元模型中,俯冲界面数据从Slab 2.0(https://www.usgs.gov/)获取。由于获取的俯冲界面深度约为400~500 km,为降低数值模拟中边界效应对研究区的影响,同时考虑到地幔深处几何界面对模拟的影响较小,俯冲界面延伸至800 km深度[22]。同样,对于研究区周边区域也采用扩张方法,使整个有限元模型明显大于本文研究区。图 2(b)为构建的研究区几何模型,模型长度为2 600 km,宽度为1 100 km,深度为800 km。在本文模型中,所有横向边界均固定为在法线方向具有零位移,但在切线方向不受约束;底面边界在垂直方向固定,但在水平方向不受约束;顶部边界在水平和垂直方向均不受约束。该设置会使断层沿板块界面滑动及地幔粘弹性松弛产生的应变在板块内部累积[23]。
在对三维实体模型进行格网划分时,为更好地计算断层破裂附近的位移精度、数值计算精度与收敛性等[24-25],突出重点研究区厄瓜多尔及海沟的构造变形,本文首先将断层面上海沟附近区域划分为边长约2 km的四面体单元,设置格网尺寸随距断层面的距离以1 ∶1.2比例逐渐增大,最终共划分734 072个四面体单元,模型共包含143 157个节点,最小格网尺寸为2 km,最大格网尺寸为110 km(图 2(b))。该方法可避免四面体划分出现高度扭曲,从而出现非收敛解和数值误差,同时在深地幔中使用粗元素可节省计算时间和成本,且不影响分辨率精度[23-24, 26]。
本文忽略震间模型的重力因素,将其视为绝对应力状态的扰动,这些应力扰动通过沿断层界面以运动学方式指定反向滑移率进行模拟[8]。同时,为使模拟结果能较客观地反映该区域构造变形特征,建模时忽略地表曲率[27]。有限元节点上的累积位移可根据其在假定笛卡尔坐标系内的原始位置进行计算。即使在远场中,地球曲率导致的水平差异也可以忽略不计,球面坐标系和笛卡尔坐标系测试模型之间的差异很小[23, 27]。此外,已有研究表明,在模拟百年尺度的震间变形时,该区域历史大地震的影响较小,因此本文在之后研究中并未考虑历史地震的影响[8]。
2.3 岩石圈流变结构配置本文采用的P波、S波速度及地壳、地幔密度、粘弹性等参数均来自文献[12]和[25]。弹性模型和粘弹性模型之间唯一的区别是地幔域是否施加粘性参数。在弹性模型中,地壳与地幔变形视为弹性回弹,无粘度系数;而在粘弹性模型中,地幔变形视为弹性变形和与时间相关的粘性行为的组合,大陆地幔与海洋地幔的粘度分别为4×1019 Pa·s和1×1020 Pa·s[10]。粘弹性材料的弹性特性(如杨氏模量、泊松比和密度)与对应弹性模型中的弹性材料相同[10]。表 1为本文模型的地块属性。
|
|
表 1 地块属性 Tab. 1 Plate properties |
对于弹性模型,由于弹性变形是与时间无关的变形行为,因此本文模拟时间尺度为1 a的地表位移。而对于具有随时间变化的变形行为的粘弹性模型,本文使用自适应时间步长方法模拟200 a的震间闭锁[8]。该方法基于本构模型和变形率返回稳定时间步长,从而捕获粘弹性材料的稳定响应[8]。对于粘弹性模型,地表速度场是从模拟的最后一个时间步长计算而来,因此该时间之后的粘弹性响应(约为Maxwell弛豫时间的10倍,已经稳定)速度可以代表地震后期速度。
本文采用Pylith有限元计算软件模拟厄瓜多尔震间闭锁效应在不同模型下的最佳闭锁深度[28]。对于大地震震后几百年的震间变形来说,双粘度Burgers材料所代表的瞬态流变学对实验的影响微乎其微,甚至对总的粘弹性贡献有所低估。而南美洲大陆板块下方海洋纳斯卡板块快速俯冲引发的大型(MW>7.5)大推力地震,其特征重现时间为100~250 a[29]。因此,本文选择忽略瞬态流变学因素,并结合Maxwell粘弹性流变学来模拟板块震间的粘弹性效应[8]。对于地幔的应力积累和长期演变过程,具有流变学特性的Maxwell粘弹性介质体能很好地模拟不同地块随时间缓慢变化的粘弹性流变特性,较好地反映地壳运动过程中产生的地表位移和应力积累过程。同时,Maxwell体也是一种与时间无关的弹性行为和与时间相关的粘性行为的组合,分别以弹性模量和粘度为特征[30]。
本文在模拟2种不同模型的震间板块运动时采用相同的反向滑动(backslip)设置,即假设一个与同震滑移相反的断层位错来模拟不同板块间相邻断裂带的震间闭锁[8, 31]。大量研究表明,反向滑移模型能较好地解释震间活动断裂附近的GPS观测[8]。本文采用文献[21]中估计的纳斯卡板块(NAZ)相对于南美板块(NA)的相对滑动速率作为约束,设置俯冲界面以55 mm/a的相对速率发生滑动,并沿N83°E方向俯冲至南美板块之下[13, 21, 32]。
对弹性和粘弹性三维模型,本文设置闭锁区深度在10~80 km内变化,根据文献[16]并间隔5 km进行设置。同时为简化模型,将断裂闭锁设置为均匀分布,共完成15个正演模型。使用均方根(root mean square, RMS)准则以量化GPS观测结果和有限元模型预测值之间的不拟合度,进而通过评估该不拟合度搜索最优的震间闭锁深度[8]。RMS计算公式为:
| $ \mathrm{RMS}=\sqrt{\frac{\sum\limits_{i=1}^n\left(V_{\text {横拟 }}-V_{\text {实测 }}\right)^2}{n}} $ | (1) |
式中,V实测为实测GPS点在东、北方向的速度分量;V模拟为有限元模型在相应点东、北方向的速度分量;n为GPS站点数。
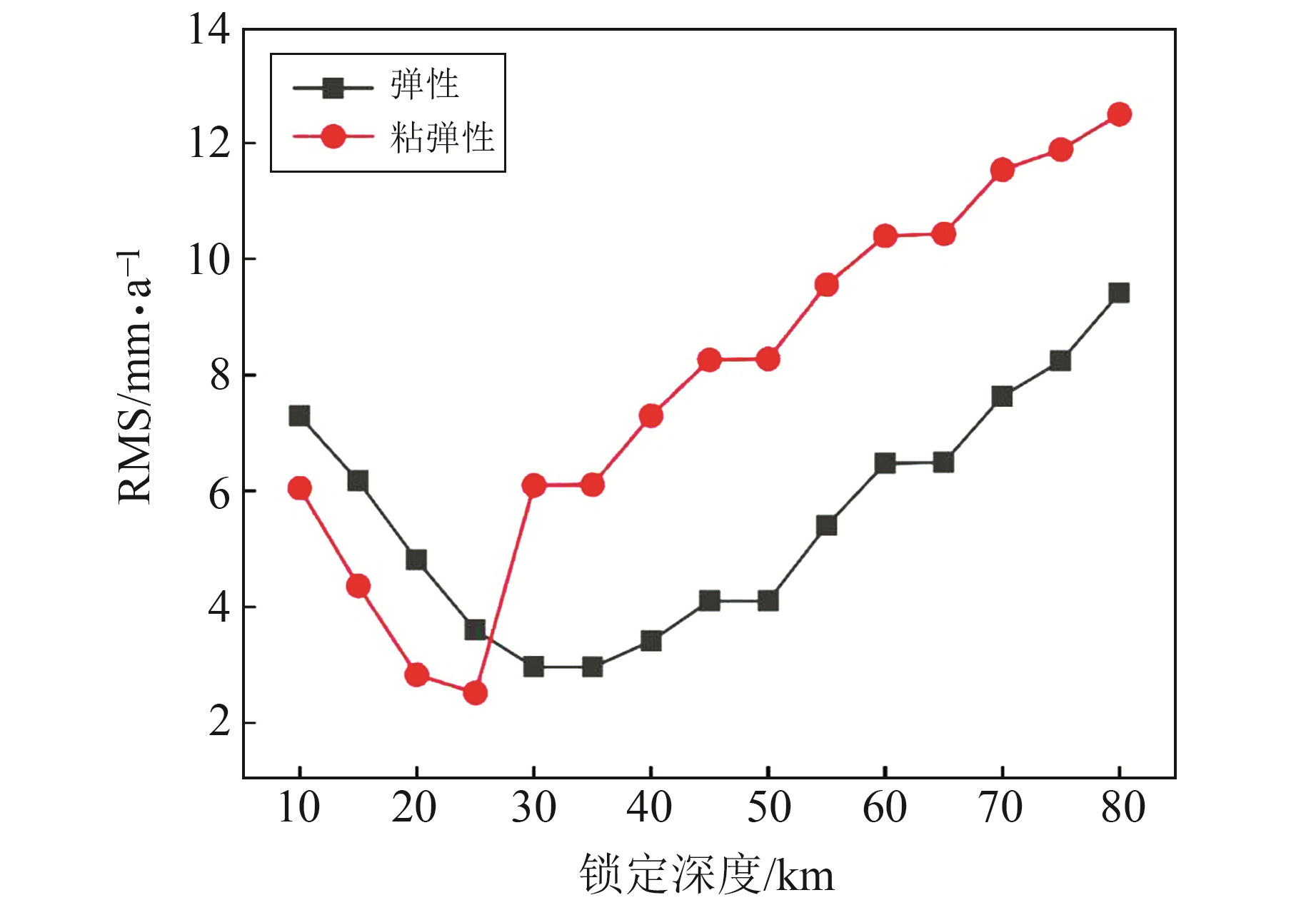
3 结果和讨论图 3为弹性模型与粘弹性模型在不同闭锁深度的模拟值与GPS实测数据的均方根分布。可以看出,两种模型表现出相近的变化趋势:随着断层闭锁深度的增加,弹性模型和粘弹性模型的RMS值先下降,达到最佳拟合后逐渐上升。另外,在断层闭锁深度为30~35 km时,弹性模型能较好地拟合GPS数据,RMS值为2.96 mm/a;而对于粘弹性模型,最佳断层闭锁深度为25 km,此时对应的RMS值为2.52 mm/a。
|
图 3 弹性模型与粘弹性模型不同闭锁深度的模拟值与GPS实测数据的均方根 Fig. 3 RMS of simulated values and GPS measured data for different locking depths of elastic and viscoelastic models |
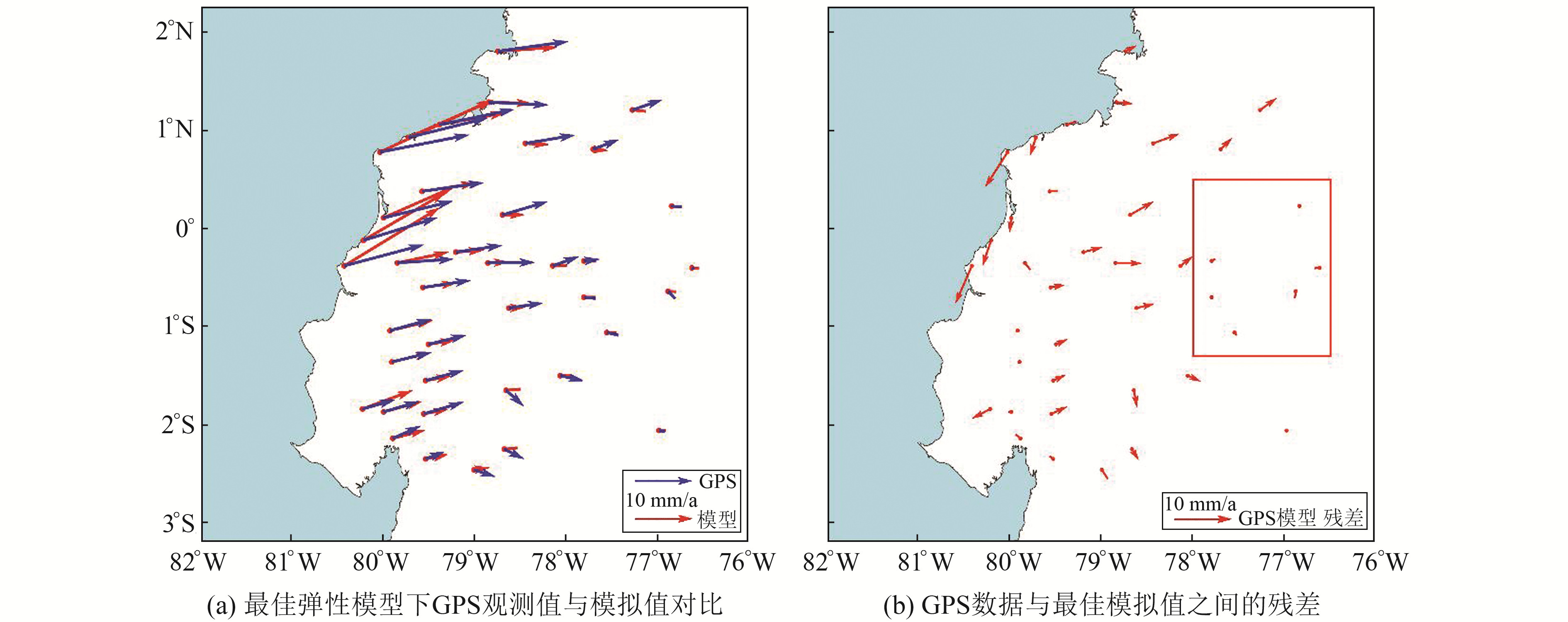
采用弹性模型计算的震间最佳闭锁深度约为30~35 km,与前人研究的秘鲁区域闭锁深度约为30~40 km较为接近[16, 21]。由图 4(a)可知,在该闭锁深度下,弹性模型结果与实测GPS速度场在大部分地区较为接近,但在靠近海沟及北部区域的差异仍较为明显。从图 4(b)可以看出,除靠近海沟的部分站点外,大部分区域均呈现出NEE向系统性残差,并与板块俯冲汇聚方向一致,表明纯弹性模型未能较好地模拟研究区震间俯冲变形机制。
|
图 4 最佳闭锁深度下GPS数据、模拟值及其残差 Fig. 4 GPS data, simulated values andtheir residuals at optimal locking depth |
粘弹性模型获得的最佳闭锁深度为25 km,与弹性模型相比(RMS为2.96 mm/a),粘弹性模型在整体上能更好地拟合厄瓜多尔地区GPS速度场,模拟值与GPS观测值的吻合度更高(RMS为2.52 mm/a),结果见图 5。虽然在远场粘弹性模型的残差稍大(图 4和5红色方框区域),但这主要是由粘弹性变形所具有的明显长波信号所致[8]。此外,远场区域的构造变形也在一定程度上受安第斯造山运动的影响,同样也可能导致模拟残差较大,因此板块的俯冲汇聚并非其唯一的构造机制[11, 16-17]。但从整体上看,相比于纯弹性模型,粘弹性模型能明显提升该区数值模拟结果与GPS数据的拟合度,更好地解释震间所观测到的形变场。分析表明,在厄瓜多尔地区,深部粘弹性软流圈在俯冲板块的推挤作用下,在震间会引起较为明显的上地壳变形,且这一变形方向与俯冲汇聚方向基本一致。

|
图 5 最佳闭锁深度下GPS数据、模拟值及及其残差 Fig. 5 GPS data, simulated values andtheir residuals at optimal locking depth |
本文以南美洲板块高精度GPS速度场为约束,结合区域活动构造特征与深部圈层结构,构建纳斯卡板块与南美洲板块在厄瓜多尔俯冲区的三维有限元动力学模型,并分别以纯弹性与纯弹性+粘弹性模型为理论基础,模拟分析厄瓜多尔地区的震间形变场,估计最佳断裂闭锁深度。结果表明,相比于弹性模型,粘弹性模型能更好地解释震间地表变形,表明深部粘弹性圈层在俯冲板块的推挤作用下会引起明显的上地壳变形。此外,基于弹性模型的最佳震间闭锁深度约为30~35 km,而基于粘弹性模型的最佳闭锁深度为25 km,进一步说明粘弹性模型同样会引起俯冲断裂闭锁分布特征的差异。今后针对该地区的地球动力学研究有必要进一步考虑深部粘弹性圈层的动力学机制。
本文关注的重点是俯冲界面闭锁深度对于弹性模型与粘弹性模型在震间影响的差异,并未考虑内陆造山运动与其他断层构造,在后续研究中会进一步精化模型,研究更复杂情况下的闭锁深度和区域流变结构。
| [1] |
Stern R J. Subduction Zones[J]. Reviews of Geophysics, 2002, 40(4)
(  0) 0) |
| [2] |
Agius M R, Rychert C A, Harmon N, et al. A Thin Mantle Transition Zone beneath the Equatorial Mid-Atlantic Ridge[J]. Nature, 2021, 589(7 843): 562-566
(  0) 0) |
| [3] |
Staller A, Álvarez-Gómez J A, Luna M P, et al. Crustal Notion and Deformation in Ecuador from cGNSS Time Series[J]. Journal of South American Earth Sciences, 2018, 86: 94-109 DOI:10.1016/j.jsames.2018.05.014
(  0) 0) |
| [4] |
Li S Y, Fukuda J, Oncken O. Geodetic Evidence of Time-Dependent Viscoelastic Interseismic Deformation Driven by Megathrust Locking in the Southwest Japan Subduction Zone[J]. Geophysical Research Letters, 2020, 47(4)
(  0) 0) |
| [5] |
赵静, 江在森, 武艳强, 等. 汶川地震前龙门山断裂带闭锁程度和滑动亏损分布研究[J]. 地球物理学报, 2012, 55(9): 2 963-2 972 (Zhao Jing, Jiang Zaisen, Wu Yanqiang, et al. Study on Fault Locking and Fault Slip Deficit of the Longmenshan Fault Zone before the Wenchuan Earthquake[J]. Chinese Journal of Geophysics, 2012, 55(9): 2 963-2 972)
(  0) 0) |
| [6] |
Tian Z, Freymueller J T, Yang Z Q. Spatio-Temporal Variations of Afterslip and Viscoelastic Relaxation Following the MW7.8 Gorkha(Nepal) Earthquake[J]. Earth and Planetary Science Letters, 2020, 532
(  0) 0) |
| [7] |
Wang K L, Hu Y, He J H. Deformation Cycles of Subduction Earthquakes in a Viscoelastic Earth[J]. Nature, 2012, 484(7 394): 327-332
(  0) 0) |
| [8] |
Li S Y, Moreno M, Bedford J, et al. Revisiting Viscoelastic Effects on Interseismic Deformation and Locking Degree: A Case Study of the Peru-North Chile Subduction Zone[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(6): 4 522-4 538 DOI:10.1002/2015JB011903
(  0) 0) |
| [9] |
张健, 赵斌, 王东振, 等. 基于2015年尼泊尔MW7.8地震震后形变探测青藏高原南缘的岩石圈流变结构[J]. 大地测量与地球动力学, 2021, 41(8): 827-832 (Zhang Jian, Zhao Bin, Wang Dongzhen, et al. Probing the Rheological Structure of Southern Tibet from the Postseismic Deformation of the 2015 MW7.8 Nepal Earthquake[J]. Journal of Geodesy and Geodynamics, 2021, 41(8): 827-832)
(  0) 0) |
| [10] |
Hu Y, Wang K, He J, et al. Three-Dimensional Viscoelastic Finite Element Model for Postseismic Deformation of the Great 1960 Chile Earthquake[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B12)
(  0) 0) |
| [11] |
Nocquet J M, Villegas-Lanza J C, Chlieh M, et al. Motion of Continental Slivers and Creeping Subduction in the Northern Andes[J]. Nature Geoscience, 2014, 7(4): 287-291 DOI:10.1038/ngeo2099
(  0) 0) |
| [12] |
Wang K L, Hu Y, He J H. Deformation Cycles of Subduction Earthquakes in a Viscoelastic Earth[J]. Nature, 2012, 484(7 394): 327-332
(  0) 0) |
| [13] |
金双根, 朱文耀. 南美板块的运动和活动形变[J]. 武汉大学学报: 信息科学版, 2002, 27(4): 358-362 (Jin Shuanggen, Zhu Wenyao. Motion and Active Deformation of South America Plate[J]. Editoral Board of Geomatics and Information Science of Wuhan University, 2002, 27(4): 358-362)
(  0) 0) |
| [14] |
Vallée M, Nocquet J M, Battaglia J, et al. Intense Interface Seismicity Triggered by a Shallow Slow Slip Event in the Central Ecuador Subduction Zone[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(6): 2 965-2 981 DOI:10.1002/jgrb.50216
(  0) 0) |
| [15] |
Pollitz F F, Bürgmann R, Segall P. Joint Estimation of Afterslip Rate and Postseismic Relaxation Following the 1989 Loma Prieta Earthquake[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B11): 26 975-26 992 DOI:10.1029/98JB01554
(  0) 0) |
| [16] |
Chlieh M, Mothes P A, Nocquet J M, et al. Distribution of Discrete Seismic Asperities and Aseismic Slip along the Ecuadorian Megathrust[J]. Earth and Planetary Science Letters, 2014, 400: 292-301 DOI:10.1016/j.epsl.2014.05.027
(  0) 0) |
| [17] |
White S M, Trenkamp R, Kellogg J N. Recent Crustal Deformation and the Earthquake Cycle along the Ecuador-Colombia Subduction Zone[J]. Earth and Planetary Science Letters, 2003, 216(3): 231-242 DOI:10.1016/S0012-821X(03)00535-1
(  0) 0) |
| [18] |
杨建, 盛书中, 万永革, 等. 1976年以来南美板缘浅源强震间应力触发研究[J]. 大地测量与地球动力学, 2018, 38(6): 634-638 (Yang Jian, Sheng Shuzhong, Wan Yongge, et al. Study on Stress Triggering of Strong Shallow-Focus Earthquakes in South America since 1976[J]. Journal of Geodesy and Geodynamics, 2018, 38(6): 634-638 DOI:10.14075/j.jgg.2018.06.017)
(  0) 0) |
| [19] |
Mora-Páez H, Kellogg J N, Freymueller J T, et al. Crustal Deformation in the Northern Andes—A New GPS Velocity Field[J]. Journal of South American Earth Sciences, 2019, 89: 76-91 DOI:10.1016/j.jsames.2018.11.002
(  0) 0) |
| [20] |
Trenkamp R, Kellogg J N, Freymueller J T, et al. Wide Plate Margin Deformation, Southern Central America and Northwestern South America, CASA GPS Observations[J]. Journal of South American Earth Sciences, 2002, 15(2): 157-171 DOI:10.1016/S0895-9811(02)00018-4
(  0) 0) |
| [21] |
Nocquet J M, Villegas-Lanza J C, Chlieh M, et al. Motion of Continental Slivers and Creeping Subduction in the Northern Andes[J]. Nature Geoscience, 2014, 7(4): 287-291 DOI:10.1038/ngeo2099
(  0) 0) |
| [22] |
Huang K J, Hu Y, Freymueller J T. Decadal Viscoelastic Postseismic Deformation of the 1964 MW9.2 Alaska Earthquake[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(9)
(  0) 0) |
| [23] |
Hashima A, Becker T W, Freed A M, et al. Coseismic Deformation Due to the 2011 Tohoku-Oki Earthquake: Influence of 3-D Elastic Structure around Japan[J]. Earth, Planets and Space, 2016, 68(1)
(  0) 0) |
| [24] |
瞿伟, 王运生, 徐超, 等. 渭河盆地构造应力场有限元数值模拟[J]. 武汉大学学报: 信息科学版, 2017, 42(12): 1 749-1 755 (Qu Wei, Wang Yunsheng, Xu Chao, et al. Tectonic Stress Field of the Weihe Basin Using the Finite Element Method[J]. Geomatics and Information Science of Wuhan University, 2017, 42(12): 1 749-1 755)
(  0) 0) |
| [25] |
Melnick D, Moreno M, Quinteros J, et al. The Super-Interseismic Phase of the Megathrust Earthquake Cycle in Chile[J]. Geophysical Research Letters, 2017, 44(2): 784-791 DOI:10.1002/2016GL071845
(  0) 0) |
| [26] |
Melnick D, Li S Y, Moreno M, et al. Back to Full Interseismic Plate Locking Decades after the Giant 1960 Chile Earthquake[J]. Nature Communications, 2018, 9(1)
(  0) 0) |
| [27] |
Hu Z P, Hu Y, Bodunde S S. Viscoelastic Relaxation of the Upper Mantle and Afterslip Following the 2014 MW8.1 Iquique Earthquake[J]. Earthquake Research Advances, 2021
(  0) 0) |
| [28] |
Aagaard B T, Knepley M G, Williams C A. A Domain Decomposition Approach to Implementing Fault Slip in Finite-Element Models of Quasi-Static and Dynamic Crustal Deformation[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(6): 3 059-3 079 DOI:10.1002/jgrb.50217
(  0) 0) |
| [29] |
Nishenko S P. Circum-Pacific Seismic Potential: 1989-1999[J]. Pure and Applied Geophysics, 1991, 135(2): 169-259 DOI:10.1007/BF00880240
(  0) 0) |
| [30] |
Hilton H H. Elastic and Viscoelastic Poisson's Ratios: The Theoretical Mechanics Perspective[J]. Materials Sciences and Applications, 2017, 8(4): 291-332 DOI:10.4236/msa.2017.84021
(  0) 0) |
| [31] |
Savage J C. A Dislocation Model of Strain Accumulation and Release at a Subduction Zone[J]. Journal of Geophysical Research: Solid Earth, 1983, 88(B6): 4 984-4 996 DOI:10.1029/JB088iB06p04984
(  0) 0) |
| [32] |
Chlieh M, Perfettini H, Tavera H, et al. Interseismic Coupling and Seismic Potential along the Central Andes Subduction Zone[J]. Journal of Geophysical Research: Solid Earth, 2011, 116(B12)
(  0) 0) |
 2023, Vol. 43
2023, Vol. 43


