2. 成都锦城学院通识教育学院,成都市西源大道1号,611731;
3. 中国地震局地震研究所,武汉市洪山侧路40号,430071;
4. 引力与固体潮国家野外科学观测研究站,武汉市洪山侧路40号,430071;
5. 武汉理工大学计算机与人工智能学院,武汉市珞狮路122号,430070
微震震源定位是微震监测技术的核心内容,也是减少地质灾害损失、加强重点工程与设施抗震减灾预警预防的关键部分,其中微震震源定位数学模型和模型解算方法是理论研究的重要基础,模型的选择或组合是提高定位精度的有效途径[1]。
群体智能优化方法是微震震源定位方法的重要手段之一。不同于单目标优化定位方法[2],多目标优化定位方法[3-4]采用2个或多个目标函数进行震源近似解寻优,相当于在单目标优化基础上增加额外的自变量寻优约束条件,使定位结果更加可靠,但针对微震震源定位数学模型组合合理性的研究较少,使其在具体应用时缺乏可靠性依据。
常见的微震震源定位模型[5]有走时模型、到时差模型(time difference of arrival, TDA)、到时差商(time difference quotient of arrival, TDQA)模型和到距差模型,虽然这些模型的目标函数在数值计算时理论值皆为0,但具有完全不同的物理意义,在进行目标优化时对含有误差的参数值具有显著的敏感性差异,使得定位目标函数过早收敛或陷入局部极值中。而物理意义相差较大的模型组合有助于减少优化过程中的数值跳跃现象,提供更加稳定的微震震源优化定位过程。
本文基于经典的微震到时差和到时差商原理构建4个微震震源定位数学模型,并设计6个微震正反演仿真实验和1个工程验证实验,结合多目标蚁狮优化(multi-objective ant lion optimization, MOALO)算法求解多目标优化模型组合。
1 微震震源定位数学模型本文将结合到时差模型和到时差商模型进行组合模型研究,并以此进行数学模型组合方案的制定。
定义Tk为2个拾震器记录到的地震波到时差,即Tk=ti-tj,且i≠j;定义Lk为2个拾震器与微震震源的空间距离差,即Lk=li-lj=vTk。根据上述关键参数建立以下4个含义不同的微震震源定位数学模型:
| $ f_1=\sum\limits_{k=1}^N\left(T_k-\frac{L_k}{v}\right)^2 $ | (1) |
| $ f_2=\sum\limits_{k=1}^N||\left(T_k-\frac{L_k}{v}\right)+\left.1\right|^2-1 \mid $ | (2) |
| $ f_3=\sum\limits_{p, q=1 ; p>q}^M\left(\frac{T_p}{L_p}-\frac{T_q}{L_q}\right)^2 $ | (3) |
| $ f_4=\sum\limits_{p, q=1 ; p>q}^M|| \frac{T_p}{L_p}-\frac{T_q}{L_q}+\left.1\right|^2-1 \mid $ | (4) |
式中,f1为经典到时差模型[5],反映观测到时差与理论到时差的偏离程度,记作TDA;f2是在f1基础上,在算术平方式内加1,然后对平方式整体减1后求取绝对值,可放大到时差偏离值幅值,避免模型在求解过程中过早结束迭代,也有利于算法发现更合适的局部最优解,使计算结果更具有可信度,记作TDA-P1;f3为经典到时差商模型倒数形式,将观测到时差作为分子,理论到达距离作为分母,包含3个或4个拾震器的地震波到时信息,可反映利用不同拾震器组合计算2个观测波速因子(
蚁狮优化(ALO)算法[6-7]是一种模仿蚁狮幼虫狩猎蚂蚁的新型群体智能优化算法,即蚁狮幼虫通过制造砂质漏斗状的陷阱诱捕随机游走的蚂蚁。ALO算法充分结合蚂蚁位置的随机性、精英策略和轮盘赌方法的优点,可增强算法的全局搜索能力,相对粒子群算法、遗传算法、杜鹃算法等具有更好的鲁棒性、收敛性与精确性。
多目标蚁狮优化算法[7]通过计算2个或多个适应度函数值得到一批Pareto最优解,并存储到指定数据集中,再使用轮盘赌选择法确定最终的寻优结果;多目标优化问题的求解模型一般为minF=
将4个模型进行两两组合,构建6个物理意义相差较大的组合模型:记模型f1和f2组合为MO-1;记模型f1和f3组合为MO-2;记模型f1和f4组合为MO-3;记模型f2和f3组合为MO-4;记模型f2和f4组合为MO-5;记模型f3和f4组合为MO-6,该组合无需测速。
3 微震震源正反演仿真实验为验证6种定位数学模型组合和多目标蚁狮优化算法在微震震源定位中的有效性,设计3组完全不同的微震源正反演仿真实验,分别为基于三维多面体台阵、二维方型台阵及一维线型台阵的微震震源定位仿真实验。
3.1 基于三维多面体台阵的微震震源定位实验实验设定地震波P波在介质中的传播速度为2 500 m/s,发震时刻记为2022-08-15 13:14:00,发震位置坐标统一设为(850, 514, 315),微震监测台阵为三维多面体型(近似球体),在其边界上均匀布设12个探测器,相关仿真数据如图 1所示。

|
图 1 仿真实验拾震器布置 Fig. 1 Seismometer layout of simulation experiment |
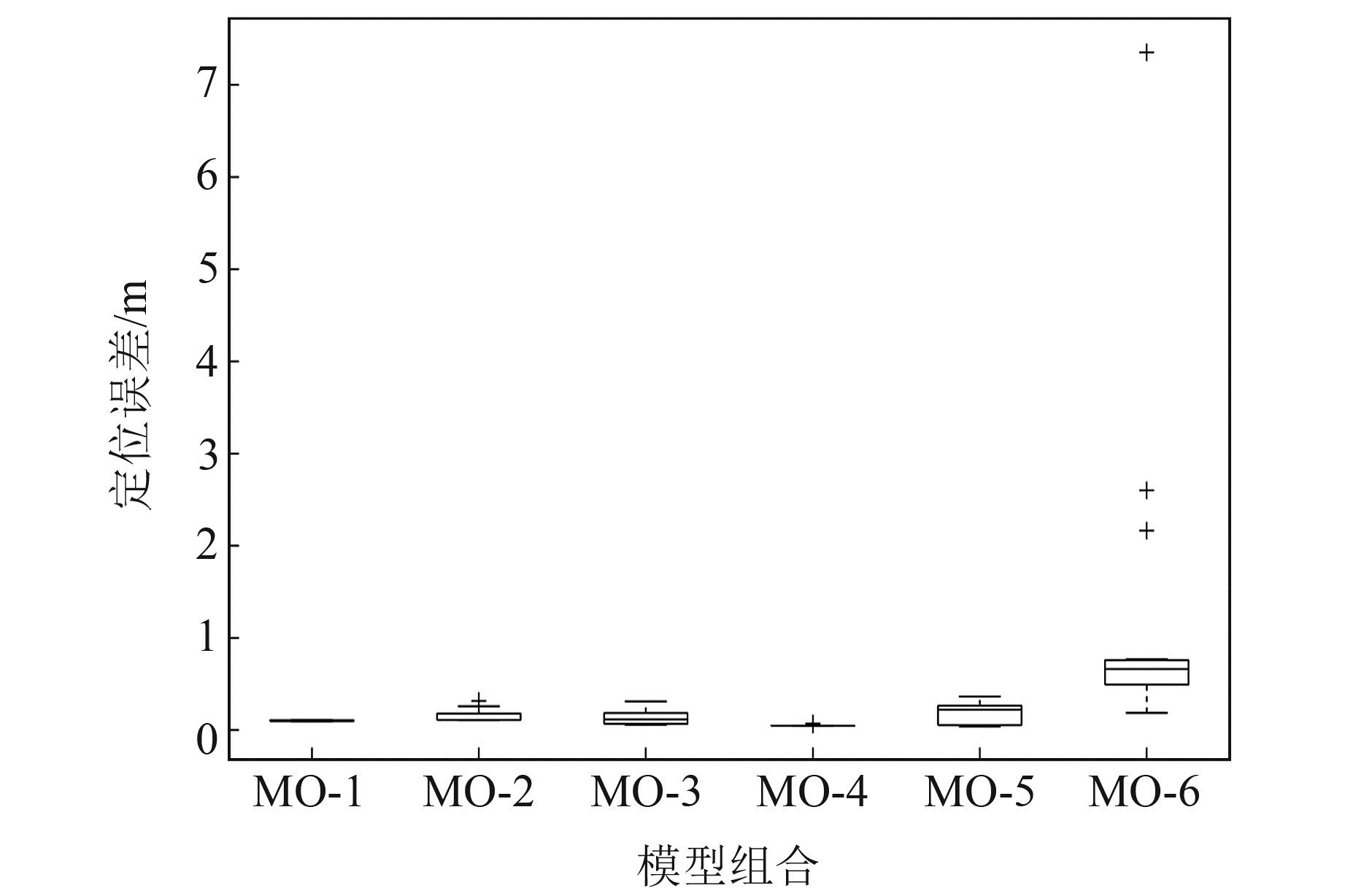
图 2为基于三维多面体台阵及不同定位数学模型组合下的微震震源定位结果,采用6个模型组合进行定位效果对比,定位结果误差定义为真实震源点与预测震源点的三维空间位置绝对距离值,包含水平向误差信息和垂直向误差信息。基于图 2中箱型、中位数、下四分位数、上四分位数等指标,6个组合的定位效果差距整体较小,MO-1和MO-4的定位效果相对显著,STD值均在0.01以下,模型非常稳健;6个组合中仅有MO-6的箱线图存在极少异常值,表征箱子扁平程度的IQR值也稍大,证明稳定性相对较差,这与构成该组合的TDQA模型和TDQA-P1模型有关,这2个模型在数学形式上消去了波速参数,使得每次计算的子模型目标函数值都极小,进而导致模型在寻找全局最优解之前过早达到迭代停止条件而停止寻优。
|
图 2 不同模型组合下的微震震源定位结果箱线图 Fig. 2 Boxplot of micro-seismic source localization of different model combinations |
表 1为基于三维多面体台阵的微震震源定位结果统计,指标Mean、IQR、STD、Best、Worst、Speed、Fit-1、Fit-2分别表示定位误差数据集的均值、四分位距、标准差、最小值、最大值及定位计算平均耗时、模型1(即组合模型中左起第1个子模型)最终适应度函数均值、模型2最终适应度函数均值。由表 2可知:1)各模型组合的多目标优化定位结果差异较大,定位精度排序为MO-4>MO-1>MO-3>MO-2>MO-5>MO-6,TDA-P1和TDQA模型组合定位Mean值达到0.048 9 m,定位精度最高,IQR和STD指标也证明该模型求解过程较稳健,定位结果未出现较大波动,适用于微震震源反演;2)MO-1~MO-3和MO-5的定位效果整体相当,具体的微震震源定位可靠性和精确性差异需要结合其他仿真实验进一步分析;3)与图 2分析相呼应,MO-6虽然在Fit-1、Fit-2指标上表现看似优异,分别达到1.617 8×10-16、7.634 0×10-7,但其子模型TDQA和TDQA-P1实际上为2个观测波速的倒数之差,理论值较小,因此适应度值极小,无法评断该模型组合的寻优效果。
|
|
表 1 基于三维多面体台阵的微震震源定位结果统计 Tab. 1 Statistics of micro-seismic source localization based on 3D polyhedral array |
|
|
表 2 微震震源正演仿真数据 Tab. 2 Simulation data of micro-seismic source forward modeling |
实验微震监测台阵为二维长方型,在边界上均匀布设8个探测器,相关仿真数据见表 2。
表 3为基于二维方型台阵的微震震源定位结果统计,由表可知:1)各模型组合的多目标优化定位结果差异较小,定位精度排序为MO-1>MO-3>MO-4>MO-2>MO-5>MO-6,TDA和TDA-P1模型组合的定位Mean值达到0.491 1 m,在多个指标(如IQR、STD、Best、Worst、Speed)上均表现较优异;2)其他模型组合的微震震源反演结果极为接近,定位精度均较高,在同等条件下可相互替换,但在其他条件下的定位性能差异需要结合其他仿真实验结果进一步分析。
|
|
表 3 基于二维方型台阵的微震震源定位结果统计 Tab. 3 Statistics of micro-seismic source localization based on 2D square array |
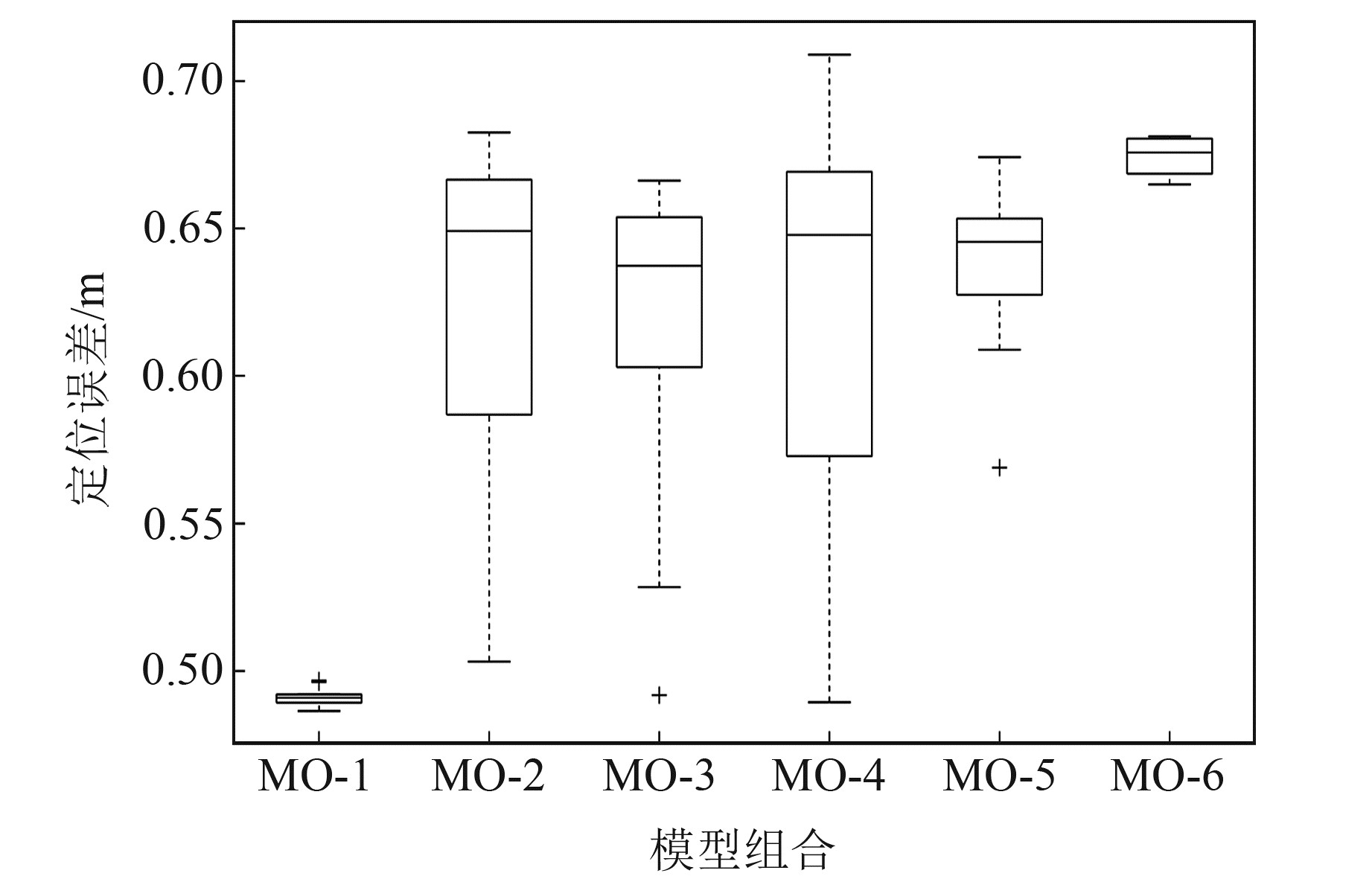
图 3为基于二维方型台阵及不同定位数学模型组合下的微震震源定位结果,可以看出,各模型组合的中位数差距不大,均在0.2 m以内,MO-1、MO-6表现更加稳健,箱型较扁;这些组合的具体定位效果差异需要结合其他实验方案综合分析。
|
图 3 不同模型组合下的微震震源定位结果箱线图 Fig. 3 Boxplot of micro-seismic source localization under different model combinations |
实验微震监测台阵为一维直线型,在边界均匀布设7个探测器,真实震源位于微震台阵外侧,相关仿真数据见表 4。
|
|
表 4 微震震源正演仿真数据 Tab. 4 Simulation data of micro-seismic source forward modeling |
表 5为基于一维直线型台阵的微震震源定位结果统计,由表可知:1)各模型组合的多目标优化定位结果差异较大,定位精度排序为:MO-4>MO-6>MO-3>MO-5>MO-2>MO-1,TDA-P1和TDQA模型组合的定位Mean值达到3.168 2 m,同时适应度函数值(1.114 5×10-11)和定位结果(0.535 7 m)也较优秀,证明该模型组合的寻优结果较为理想,定位精度更高;2)其他组合模型中TDA与TDQA-P1和TDQA与TDQA-P1也具有良好的微震震源定位效果,仅次于MO-4;3)MO-5虽然在稳健性指标上表现优异,仅为0.052 6,但定位精度不高,多次定位结果的误差均超过40 m,定位效果未达到预期。
|
|
表 5 基于一维直线型台阵的微震震源定位结果统计 Tab. 5 Statistics of micro-seismic source localization based on linear array |
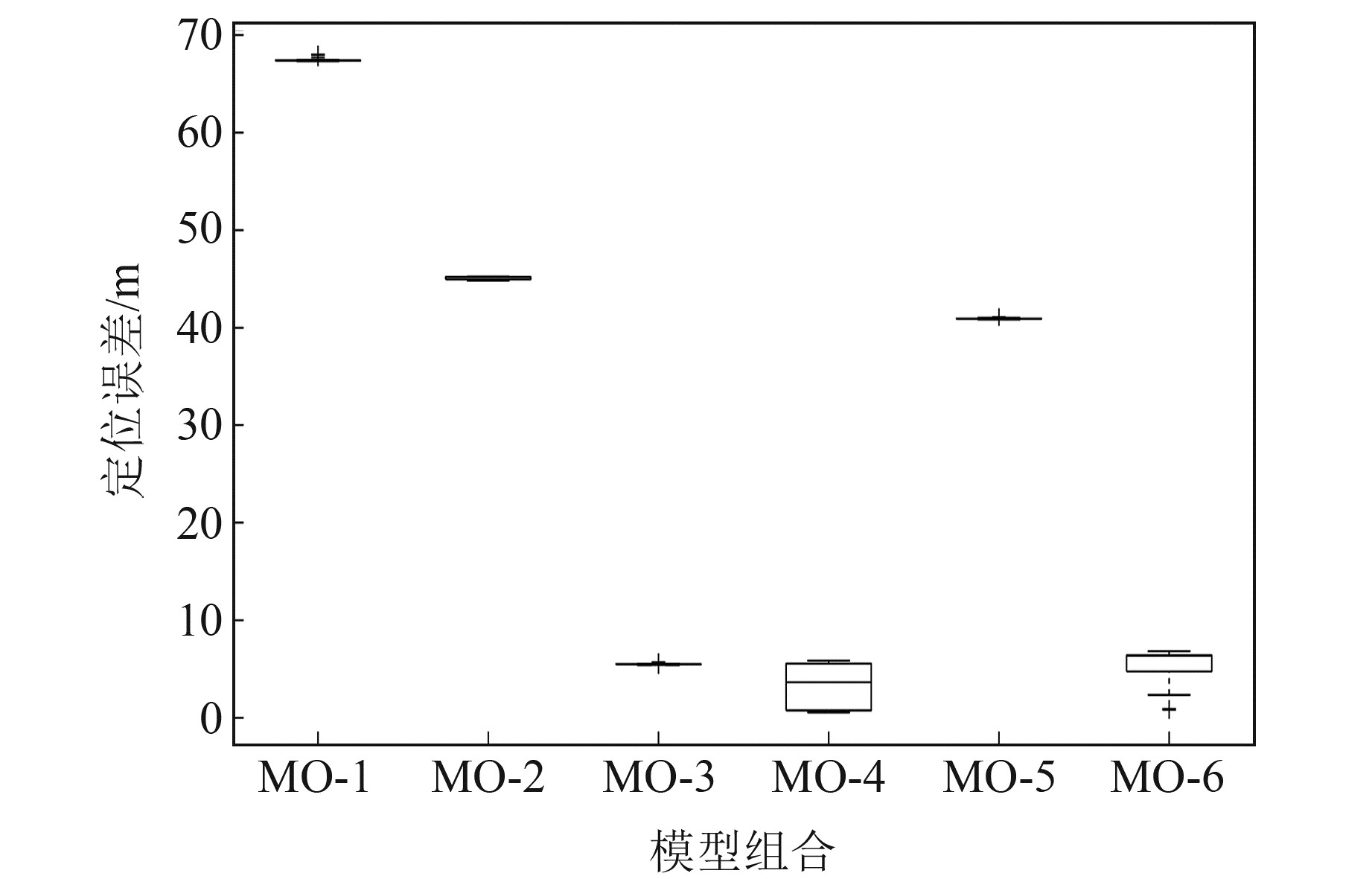
图 4为基于一维直线型台阵及不同定位数学模型组合下的微震震源定位结果,由图可知,MO-3、MO-4、MO-6中位数较小,均在10 m以下;MO-1、MO-2、MO-4箱型较扁平,定位结果随实验次数的变化较平稳,但定位结果中位数较高,不适用于微震震源定位。
|
图 4 不同模型组合下的微震震源定位结果箱线图 Fig. 4 Boxplot of micro-seismic source localization under different model combinations |
采用某深部开采矿井微震实验数据[5]进行验证,该矿井共安装12个微震监测单元,人工爆破位置为[3500.0, 3520.5, 102.0],起爆时刻为00:00,爆破成功后观测到9个P波到时数据,分别记为T1~T12。实验仿真阶段采用MATLAB 2019A数据处理工具及相应的标准函数工具箱,算法中统一预设参数为:群体搜索代理数目为20,最大迭代次数为500,目标维数为3,搜索下限为[3 000, 3 000, 50],搜索上限为[5 000, 4 000, 200],初值为[0, 0, 0],定位实验循环次数为20次。
图 5为不同定位数学模型组合下的微震震源定位结果,由图可知:1)MO-6的箱型较扁,IQR值也较小,定位结果具有较强的集聚性,但异常点较多且中位数位于300左右,无法应用于精度要求较高的微震监测中;2)MO-4的中位数相对最小,仅为150左右,同时箱高(IQR值)仅次于MO-6,定位效果较显著;3)MO-5的箱型与MO-4较类似,但中位数稍高且模型不太稳健,适合作为MO-4的替代方案;4)其他组合(MO-1~MO-3)的箱型极为类似,定位精度较低,波动范围较广,皆不适合作为微震震源定位的多目标优化模型方案。

|
图 5 不同模型组合下的微震震源定位结果箱线图 Fig. 5 Boxplot of micro-seismic source localization under different model combinations |
表 6为基于某深部开采微震事件的定位结果统计,由表可知:1)各模型组合的定位结果差异较大,定位精度排序为MO-5>MO-4>MO-1>MO-6>MO-3>MO-2,TDA-P1和TDQA-P1模型组合的定位Mean值为150.373 0 m,在所有模型组合中定位精度最高,但在IQR、STD、Fit-1、Fit-2等多个指标上不是最优值,在模型稳定性上还有一定的优化改进空间;2)MO-4与MO-5具有高度相似的微震震源定位效果,Mean值仅相差3.490 2 m,且在IQR、STD、Fit-1、Fit-2等多个指标上MO-4略优于MO-5,在可靠性要求较高的场合MO-5可作为MO-4的替代方案;3)其他组合的定位误差较大且不稳健,不宜用于实际微震震源定位。
|
|
表 6 基于某深部开采矿井的微震震源定位结果统计 Tab. 6 Statistics of micro-seismic source localization of a certain deep mining mine |
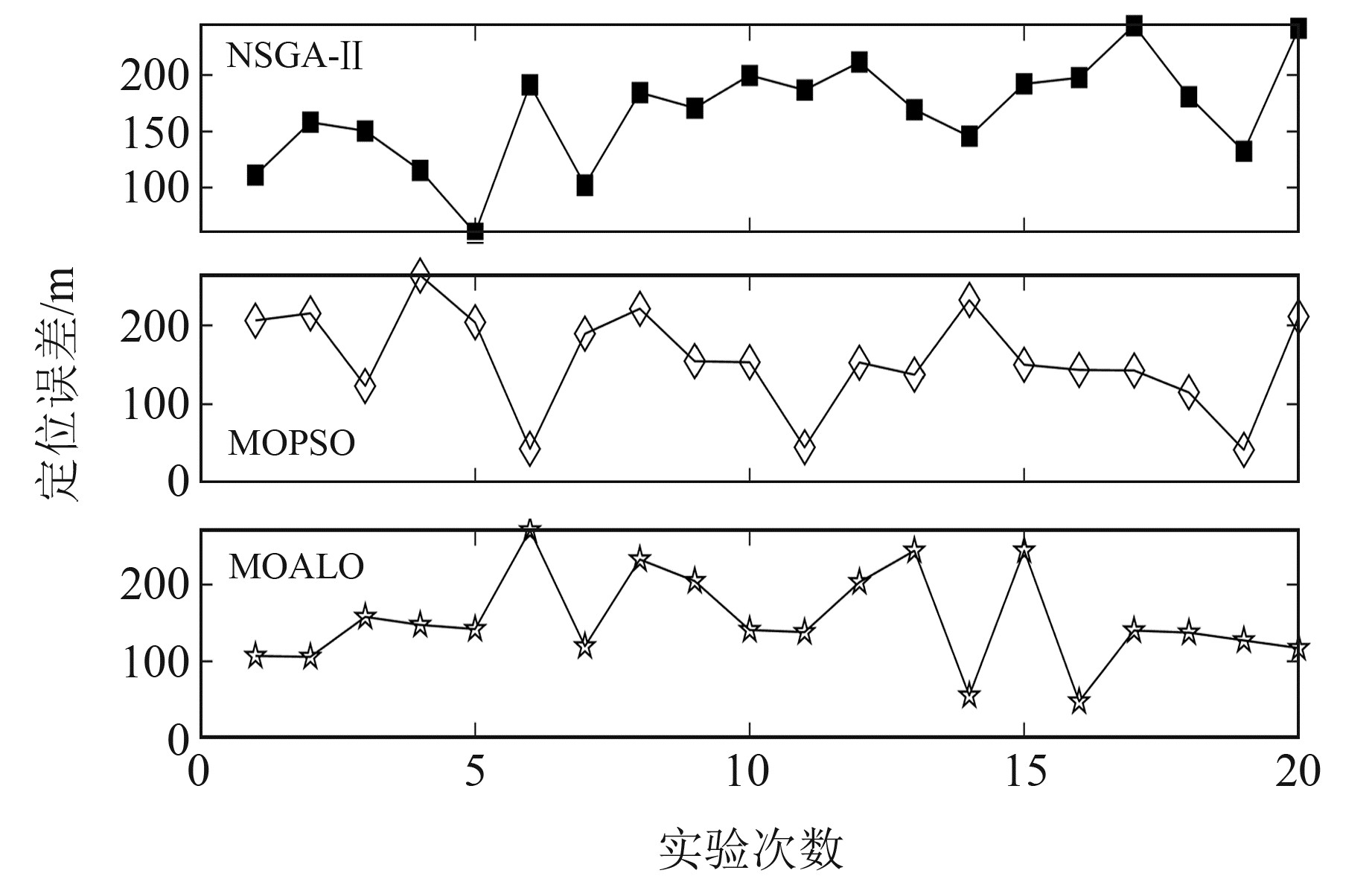
为验证MOALO在同类方法中的优势,统一采用定位性能表现相对稳健的MO-4组合作为多目标优化实验的数学模型,并采用多目标遗传算法(NSGA-Ⅱ)、多目标粒子群算法(MOPSO)来对比验证其定位效果,表 6和图 6为3种多目标优化模型下的微震震源定位结果,其他实验条件与前述实验相同。
|
图 6 3种多目标优化模型下的微震震源定位结果 Fig. 6 Micro-seismic source localization results of three multi-objective models |
整体来看,相对于NSGA-Ⅱ方法定位误差较大、全局搜索能力不理想及MOPSO方法对模型求解的效率较低等不利情况,MOALO方法具有一定的优越性,其定位精度较高且无明显的指标性缺陷,是一种较为可靠的微震震源定位方法。
5 结语本文通过讨论部分微震震源定位数学模型组合之间的性能差异和多目标蚁狮优化算法在震源定位中的应用效果,得到以下结论:
1) 将多目标智能群体优化应用到微震震源定位数学模型求解中,可增加非线性问题求解的约束条件,相对于单目标优化定位的结果更加稳定,波动性或随机性更小,能有效避免寻优过程过早陷入局部最优,实际应用时具有更大的可靠性。
2) 在经典到时差模型和到时差商模型基础上,结合算术平方和添一法思想进行标准形式的变形,分析6种模型组合的微震震源定位效果差异,认为TDA-P1与TDQA的MO-4模型组合定位性能最佳,在精度和稳定性上均有显著表现。
3) 微震监测台网形状对定位精度存在一定影响。在同等实验条件下,三维空间台阵、二维平面台阵和一维线型台阵的定位误差均值分别为0.286 5 m、0.612 7 m、27.901 7 m,实际微震监测台网布设工作中,在不考虑拾震器布设成本和安装难度的前提下,应当选择形状较为复杂、空间覆盖范围较大的台阵,可有效提高微震震源定位的精度。
| [1] |
李翔, 徐奴文. 微震震源定位研究现状及展望[J]. 地球物理学进展, 2020, 35(2): 598-607 (Li Xiang, Xu Nuwen. Research Developments and Prospects on Microseismic Source Location[J]. Progress in Geophysics, 2020, 35(2): 598-607)
(  0) 0) |
| [2] |
尹奇峰, 潘冬明, 郭全仕, 等. 基于快速模拟退火算法的井中微地震事件定位反演[J]. 地球物理学进展, 2019, 34(5): 1 954-1 961 (Yin Qifeng, Pan Dongming, Guo Quanshi, et al. Inversion of Borehole Microseismic Event Location Based on Fast Simulated Annealing Algorithm[J]. Progress in Geophysics, 2019, 34(5): 1 954-1 961)
(  0) 0) |
| [3] |
郭一楠, 崔宁, 程健. 基于MOPSO-SA混合算法的矿山微震震源定位方法[J]. 煤炭科学技术, 2020, 48(3): 126-132 (Guo Yinan, Cui Ning, Cheng Jian. Microeismic Source Localization Method Based on Hybrid Algorithm of MOPSO-SA[J]. Coal Science and Technology, 2020, 48(3): 126-132)
(  0) 0) |
| [4] |
李绍红, 朱建东, 白兰英, 等. 联合信息融合和解析方法的微震源定位研究[J]. 煤炭学报, 2018, 43(4): 1 065-1 071 (Li Shaohong, Zhu Jiandong, Bai Lanying, et al. Study on Micro-Seismic Source Location with Information Fusion and Analytical Methods[J]. Journal of China Coal Society, 2018, 43(4): 1 065-1 071)
(  0) 0) |
| [5] |
李楠, 王恩元, 孙珍玉, 等. 基于L1范数统计的单纯形微震震源定位方法[J]. 煤炭学报, 2014, 39(12): 2 431-2 438 (Li Nan, Wang Enyuan, Sun Zhenyu, et al. Simplex Microseismic Source Location Method Based on L1 Norm Statistical Standard[J]. Journal of China Coal Society, 2014, 39(12): 2 431-2 438)
(  0) 0) |
| [6] |
Ali E S, Elazim S M A, Abdelaziz A Y. Ant Lion Optimization Algorithm for Renewable Distributed Generations[J]. Energy, 2016, 116: 445-458
(  0) 0) |
| [7] |
Soesanti I, Syahputra R. Multiobjective Ant Lion Optimization for Performance Improvement of Modern Distribution Network[J]. IEEE Access, 2022, 10: 12 753-12 773
(  0) 0) |
2. College of General Education, Chengdu Jincheng College, 1 Xiyuan Road, Chengdu 611731, China;
3. Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China;
4. National Observation and Research Station for Gravitation and Solid Earth Tides, 40 Hongshance Road, Wuhan 430071, China;
5. School of Computer Science and Artificial Intelligence, Wuhan University of Technology, 122 Luoshi Road, Wuhan 430070, China
 2023, Vol. 43
2023, Vol. 43


