2. 东华理工大学江西省数字国土重点实验室,南昌市广兰大道418号,330013;
3. 江西九江扬子块体东部地球动力学野外科学观测研究站,江西省九江市星光大道138号,332006;
4. 江西省防震减灾与工程地质灾害探测工程研究中心,南昌市广兰大道418号,330013
当区域应变能积累到一定阈值时,会以地震的形式释放[1],因此开展应变观测,为地震趋势判断提供科学依据,对地震预测具有重要意义[2]。学者们通常利用全球定位系统(GPS)技术监测速度场来分析区域应变[3],但江西地区GPS地壳形变监测站分布稀疏,存在测点覆盖不足的缺陷[4]。2007年九江地震台开展了数字化地球物理应变观测,弥补了这一缺陷。区域应变受气象及区域地质构造等条件的影响[5],二维数值模型难以适应复杂的地形,因此在得不到解析解的情况下,可采用有限元分析建立区域地质模型[6],而利用数字高程模型(DEM)数据可快速建立三维地质模型,用于有限元分析,可更直观地反映应力及应变分布[7]。本文利用DEM数据建立有限元三维地质模型,采用有限元分析软件ANSYS模拟九江地震台附近区域有限元应变解,同时结合九江地震台实测温度和应变数据,分析有限元建模与实测应变的关系。
1 地震台区域三维建模 1.1 台址环境本文以九江地震台附近区域为例进行有限元建模。九江地震台(29.65°N,116.01°E,海拔110 m)位于江西北部庐山西北侧山脚,庐山山体为NE-SW向伸展的褶皱断块山体,整体呈肾状。观测山洞内温差较小,洞体基岩为硅质灰岩[8],洞内配置有SS-Y型伸缩仪、水管仪和垂直摆等形变观测仪器,观测数据质量较好。
1.2 数字化三维地形建模采用GDEMV2分辨率为30 m的DEM数据(www.gscloud.cn)进行台站区域数字化三维地形建模,研究区域范围为29.41°~29.66°N、115.86°~116.08°E。首先,利用DEM数据提取等高线;然后,利用等高线在AutoCAD软件中生成三维格网;最后,将三维格网导入Rhino软件,生成数字化三维地形模型(图 1)。数字化三维地形模型可作为有限元分析的基础地形模型,后续还需加入区域地质岩石特性来构建有限元三维地质模型。

|
图 1 九江地震台区域数字化三维地形模型 Fig. 1 Digital 3D terrain model of Jiujiang seismic station area |
考虑到实际区域地质环境存在局部破裂或岩性不均一等情况,在进行有限元三维地质建模时对地形构造要素及岩性模块进行均一化处理。根据江西省地矿局九一六大队2003年绘制的庐山地质图[9],将九江地震台附近区域划分为不同岩性模块(图 2),并在有限元建模软件中对不同岩性模块设定对应的岩石物理力学参数[10-11](表 1),构建有限元三维地质模型,以进行有限元模型数据解算。

|
图 2 模型划分与岩石的分布 Fig. 2 Division of models and distribution of rocks |
|
|
表 1 岩石物理力学参数 Tab. 1 Mechanical parameters of rock |
有限元模型数据的解算需选取合理的网格单元,以避免出现因网格过密导致计算机运行崩溃或因网格过疏导致数据解算准确度不够等情况。九江地震台区域范围的几何模型规模为km级,故选取网格尺寸为1 000 m。有限元三维地质模型存在多个块体,需明确块体间的接触关系,因无法确定不同块体岩层间的摩擦系数和粘合系数,假设岩层间无滑脱现象,采用直接绑定接触确定荷载的传递方式[12]。另外,有限元模型数据解算的关键是设置模型边界条件,即对模型施加约束,并施加重力和热载荷,为防止模型移动,最底端采用固定约束。施加的重力载荷设置为标准地球重力常数值9.806 6 m/s2,施加的热荷载为温度变化值。
2.1 热应变解算因九江地震台区域环境温度四季变化显著,月均温度变化在0~30 ℃之间,而庐山地区海拔为1 474 m,温度受地形高度影响较大,底部至顶端有约9 ℃的温差。因此,仅需设置有限元模型底部温度,再将模型从低到顶均分为4个层次,每上升一个层次温度递降3 ℃。
在有限元模型数据解算过程中,设置4种模型底部温度条件(0 ℃、10 ℃、20 ℃、30 ℃),并对不同高度施加不同温度的热荷载。4种温度条件下有限元模型热应变的解算结果(图 3)反映了九江地震台区域环境因温度造成的应变差异:温度升高时,热应变增大,山体应变不断增大,处于拉张状态;温度降低时,热应变减小,山体应变不断减小,处于压缩状态;山体顶端温度最低,其热应变总是低于山体底部。

|
图 3 施加不同温度载荷的热应变 Fig. 3 Thermal strain solution for applying different temperature loads |
有限元模型除了能求解热应变外,还能求解区域任意方向的应变。设定模型底部的热载荷温度为30 ℃,NS向和EW向的应变分别如图 4(a)和4(b)所示。因地质构造和温度的差异,不同位置及高度的应变不同。NS向与EW向应变的最大值总是出现在山体底部,最小值总是出现在山体顶端,其余部分的应变情况保持在一定范围内,有限元模型定向应变均值的量级为10-5。

|
图 4 30 ℃温度时的定向应变 Fig. 4 Directional strain solution at 30 ℃ temperature |
有限元建模的应变解算反映的是研究区域的应变分布,存在假设和简化处理,而实测应变反映的则是台站应变仪器处的点应变状态,具有基准性。如果2种应变结果存在较好的关联性,说明有限元建模应变解算结果是可靠的。
3.1 模型热应变与实测应变比较有限元模型热应变随温度及方位的变化而变化。根据2011~2021年九江地震台实测的外界温度(图 5(a)),均一化处理得到每月对应温度,求解每月对应温度下的热应变(图 5(b)),并与实测NS向及EW向应变(图 5(c)和5(d))进行比较。结果发现,有限元模型热应变均值与实测应变值的量级大小皆为10-5;模型热应变曲线与实测应变曲线存在基本相同的年周期变化,实测应变曲线的相位有所滞后。实测应变曲线年变周期不明显且幅度较小,原因是实测应变的仪器处于山洞之中,存在消除温度干扰的措施,洞内年变温度小于1 ℃,仪器受温度的影响很小。如果仪器与有限元模型具有相同的温度环境,实测应变的年变周期形态会显著接近模型热应变,说明有限元模型热应变与实测应变具有较好的一致性。
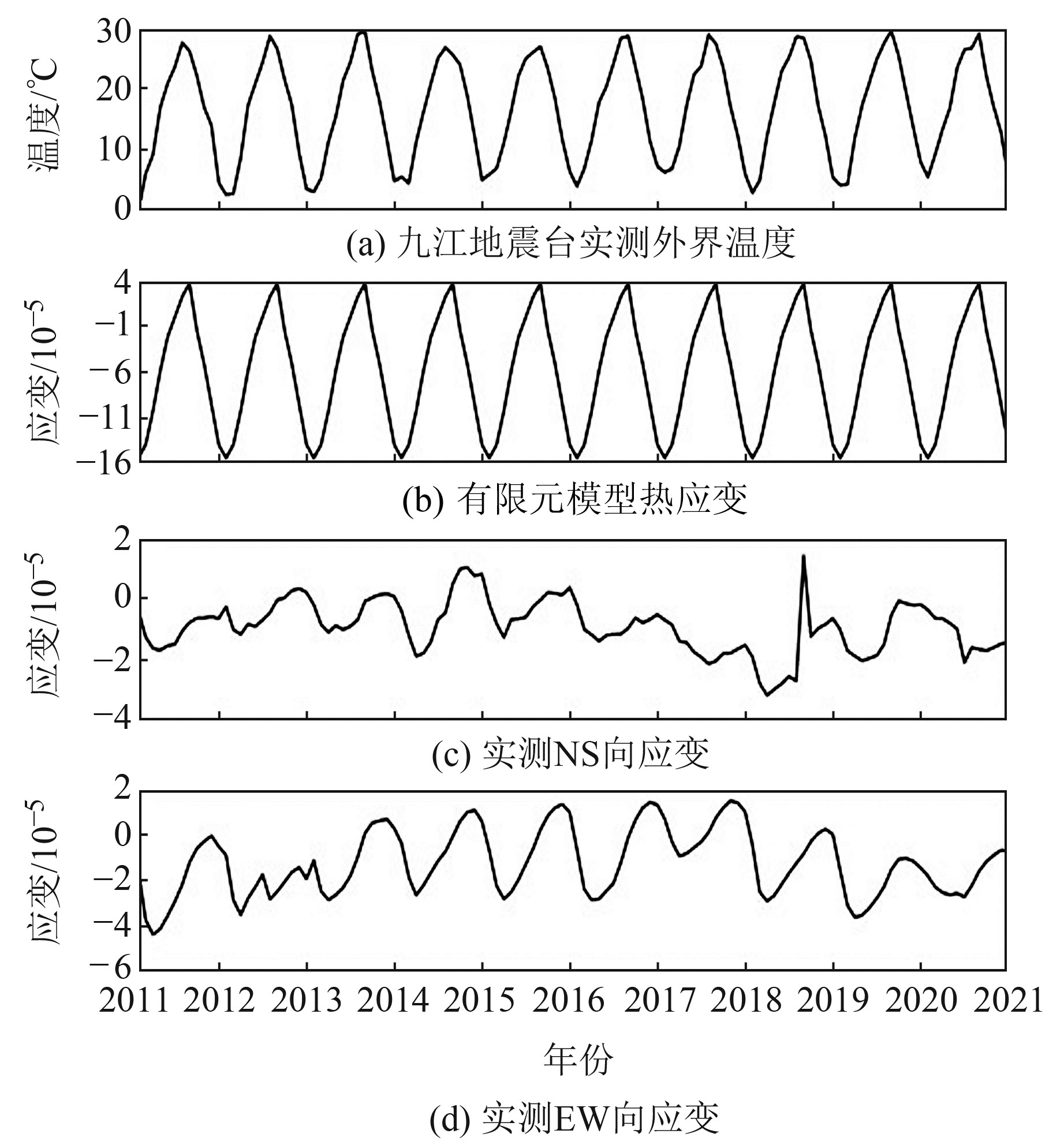
|
图 5 有限元模型热应变与实测应变比较 Fig. 5 Comparison of thermal strain and measured strain of finite element model |
利用有限元模型解算每月对应温度下的应变,并与实测应变进行比较,结果如图 6所示。在有限元模型构建过程中,因模型简化及岩性均一化处理,有限元建模应变计算结果仅为概略值,模型中每个点的应变各有不同,故有限元分析的应变解算取值为区间值。图 6中,有限元模型定向应变的均值量级为10-5,与实测应变观测结果量级一致,且实测NS向及EW向应变完全在有限元分析的定向应变区间内;有限元模型定向应变解算区间值存在明显的年周期变化,而实测应变客观上也存在年周期变化,只是相位滞后较大。实测应变曲线的年变周期不明显,且幅度较小,其原因与有限元模型热应变和实测应变比较中的阐述相同,由此说明有限元模型的定向应变解算在一定程度上能反映区域应变状态。
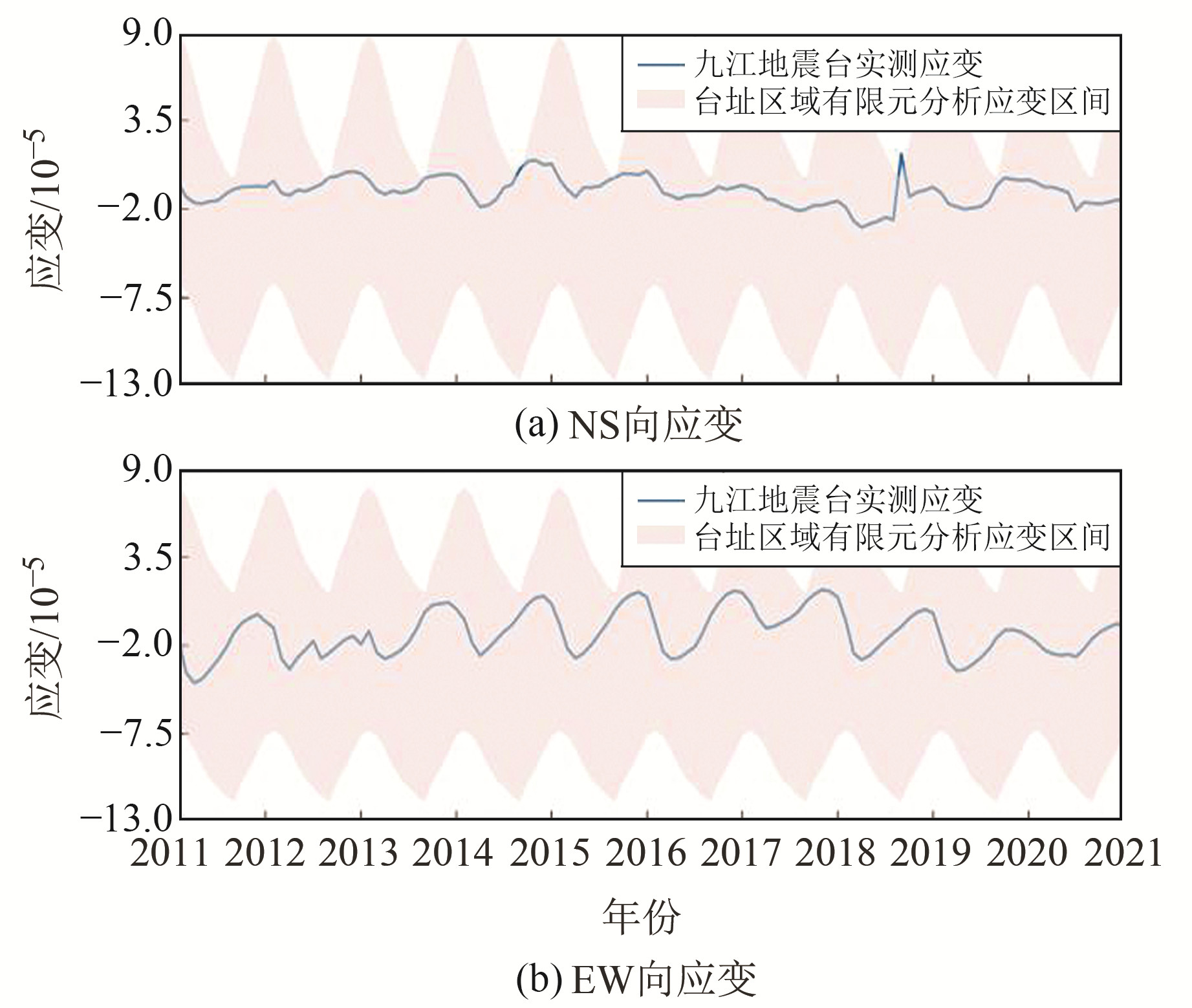
|
图 6 有限元模型定向应变与实测应变比较 Fig. 6 Comparison between finite element model directional strain and measured strain |
本文基于九江地震台实测温度和应变数据,对有限元建模进行分析,结果表明:
1) 有限元模型解算的热应变均值和定向应变均值与九江地震台实测应变结果具有相同的量级,皆为10-5。
2) 有限元模型解算的热应变和定向应变与实测应变的变化趋势基本一致,均呈现出较为明显的年周期变化特征。由于山洞内存在保温措施,使实测应变的年变周期不明显,且变化幅度较小;实测应变的相位相对有限元建模应变有所滞后,原因是外界温度传导至山洞内需要一定时间。
3) 有限元建模应变与实测应变之间存在合乎逻辑的内在联系,验证了利用数字高程模型数据和岩性参数建立有限元三维地质模型以分析区域应变的方法具有可行性。
| [1] |
谢富仁, 崔效锋, 赵建涛, 等. 中国大陆及邻区现代构造应力场分区[J]. 地球物理学报, 2004, 47(4): 654-662 (Xie Furen, Cui Xiaofeng, Zhao Jiantao, et al. Regional Division of the Recent Tectonic Stress Field in China and Adjacent Areas[J]. Chinese Journal of Geophysics, 2004, 47(4): 654-662)
(  0) 0) |
| [2] |
李宏伟, 刘瑞春, 陈永前. 山西南部区域应变场演化与地震关系的数值模拟[J]. 山西地震, 2018(4): 7-10 (Li Hongwei, Liu Ruichun, Chen Yongqian. Numerical Simulation of the Relationship between Regional Strain Field Evolution and Earthquake in Southern Shanxi Province[J]. Earthquake Research in Shanxi, 2018(4): 7-10)
(  0) 0) |
| [3] |
马娜. 基于GPS观测资料的区域地壳形变-应变特征研究[D]. 西安: 长安大学, 2012 (Ma Na. Study on Regional Crustal Deformation—Strain Characteristics Based on GPS Observation Data[D]. Xi'an: Chang'an University, 2012)
(  0) 0) |
| [4] |
刘孙君. GPS约束下青藏高原地壳运动位移场模拟及应力应变分析[D]. 武汉: 中国科学院测量与地球物理研究所, 2003 (Liu Sunjun. Numerical Simulation for Displacement of Crustal Movement in Tibetan Plateau and Stress, Strain Analysis Constrained by GPS Data[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2003)
(  0) 0) |
| [5] |
赵爱平, 周红艳, 罗建明. 九江地震台洞体应变观测环境影响分析[J]. 地震地磁观测与研究, 2015, 36(1): 107-115 (Zhao Aiping, Zhou Hongyan, Luo Jianming. Study on the Mechanism of the Cave Observation Strain Abnormities Resulted in the Observation Condition Factors' Changing in Jiujiang Seismic Station[J]. Seismological and Geomagnetic Observation and Research, 2015, 36(1): 107-115)
(  0) 0) |
| [6] |
马栋, 屈曼, 侯晓真, 等. 形变异常分析中的数值计算问题及讨论[J]. 国际地震动态, 2018, 48(8): 108-109 (Ma Dong, Qu Man, Hou Xiaozhen, et al. Numerical Calculation Problems and Discussion in Deformation Anomaly Analysis[J]. Progress in Earthquake Sciences, 2018, 48(8): 108-109)
(  0) 0) |
| [7] |
赵凤仙, 郭明珠, 胡海芹, 等. 基于数字高程模型的山谷地形效应分析[J]. 地震研究, 2016, 39(4): 598-604 (Zhao Fengxian, Guo Mingzhu, Hu Haiqin, et al. Research on Terrain Effect of Valley Based on Digital Elevation Model[J]. Journal of Seismological Research, 2016, 39(4): 598-604 DOI:10.3969/j.issn.1000-0666.2016.04.009)
(  0) 0) |
| [8] |
赵爱平, 李传江, 周红艳, 等. 九江地震台异源流体力加卸载过程的应变分析[J]. 大地测量与地球动力学, 2012, 32(增1): 67-71 (Zhao Aiping, Li Chuanjiang, Zhou Hongyan, et al. Research on Strain from Loading and Unloading Processes of Different Fluid Force in Jiujiang Seismostation[J]. Journal of Geodesy and Geodynamics, 2012, 32(S1): 67-71)
(  0) 0) |
| [9] |
杨帆, 宋传中, 任升莲, 等. 庐山变质核杂岩的变质变形及构造意义[J]. 地质论评, 2015, 61(4): 752-766 (Yang Fan, Song Chuanzhong, Ren Shenglian, et al. Metamorphism and Deformation of the Lushan Metamorphic Core Complex and Their Tectonic Significance[J]. Geological Review, 2015, 61(4): 752-766)
(  0) 0) |
| [10] |
孙东生, 赵卫华, 郭彬彬, 等. 岩石热膨胀系数实验及在ASR地应力测量中的应用[C]. 2014年中国地球科学联合学术年会, 北京, 2014 (Sun Dongsheng, Zhao Weihua, Guo Binbin, et al. Experiment on Thermal Expansion Coefficient of Rock and Its Application in ASR Geostress Measurement[C]. 2014 Annual Meeting of Chinese Geoscience Union(CGU), Beijing, 2014)
(  0) 0) |
| [11] |
叶金汉, 郗绮霞, 夏万仁. 岩石力学参数手册[M]. 北京: 水利电力出版社, 1991 (Ye Jinhan, Xi Qixia, Xia Wanren. Manual of Rock Mechanics Parameters[M]. Beijing: Water Resources and Electric Power Press, 1991)
(  0) 0) |
| [12] |
龚丽文, 邓志辉, 陈丽娟, 等. 基于台址构造环境的有限元建模分析——以黔江台为例[J]. 地震学报, 2019, 41(1): 80-91 (Gong Liwen, Deng Zhihui, Chen Lijuan, et al. Analyses of Finite Element Model Based on Station's Tectonic Environment: Taking Qianjiang Station for Example[J]. Acta Seismologica Sinica, 2019, 41(1): 80-91)
(  0) 0) |
2. Key Laboratory for Digital Land and Resources of Jiangxi Province, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China;
3. Observatory for Geodynamic of the East Yangtze Block in Jiujiang, Jiangxi Province, 138 Xingguang Road, Jiujiang 332006, China;
4. Engineering Research Center for Seismic Disaster Prevention and Engineering Geological Disaster Detection of Jiangxi Province, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China
 2023, Vol. 43
2023, Vol. 43


