2. 苏州科技大学北斗导航与环境感知研究中心,江苏省苏州市学府路99号,215009
全球气压温度(global pressure and temperature, GPT)模型是目前国内外广泛使用的经验模型之一[1-4]。该模型考虑了气压和温度的年周期变化,仅输入时间及坐标即可得到地表任意处的气压、温度、水汽压和Tm等气象参数,有效解决了大量GNSS站点缺乏气象参数的问题。GPT系列模型已成为获取地表气象参数的主要方式之一,也是目前最为普及的先验对流层延迟模型之一[1, 3, 5],全球许多学者使用并分析了其在不同时空条件下的模型精度和可用性。研究表明,受时空变化影响,GPT系列模型经过一定的函数改进后可在一定区域内减弱周期性偏差,而附带高程的Emardson-H模型则具有更好的模型精度和适用性[4, 6-11]。
本文基于美国怀俄明州立大学提供的探空资料,首先分别分析GPT3模型的气压、温度、水汽压及加权平均温度(Tm)等气象参数偏差的变化规律,再构建一种基于Emardson-H的GPT3改进模型,并将其与原模型进行对比,验证GPT3改进模型的精度及其在长三角地区的适用性。
1 数据来源及处理方法 1.1 数据来源本文使用的2015~2019年长三角地区气象参数均是怀俄明大学提供的探空产品(http://weather.uwyo.edu/upperair/),其中2015~2016年GPT3模型与探空资料的偏差用于建立基于Emardson-H的GPT3改进模型,2017~2019年的探空资料用于验证该模型的精度。
1.2 Tm计算方法基于数值积分法和探空资料计算Tm,实现步骤简单且计算精度较高,可作为真值评估GPT3模型及其改进模型的精度。具体计算方法参考文献[11-14]。
1.3 GPT3模型基于ECMWF建立的GPT3模型[3]是目前国内外广泛使用的先验对流层延迟模型之一,该模型只需提供台站的近似坐标大地经度、大地纬度、大地高(B, L, H)和年积日(doy)即可获取必需的气象参数(http://ggosatm.hg.tuwien.ac.at/DELAY/)。计算方法参考文献[3]。
1.4 Emardson-H建模方法Emardson等[4]借助K值的时空变化特性,再结合欧洲提供的数10个探空站数据,构建了一种新的K值模型,该模型只与纬度和年积日有关。由于Emardson模型与气象参数无关,直接利用测站纬度和年积日计算,且精度较好,因此可以很好地运用在实时GNSS水汽反演中,提高实时监测中短期天气的精度。忽略高程因素影响的Emardson模型公式为:
| $ \begin{array}{c} K=a_0+a_1 \varphi+a_2 \sin \left(2 \pi \frac{\text { doy }}{365.25}\right)+ \\ a_3 \cos \left(2 \pi \frac{\text { doy }}{365.25}\right) \end{array} $ | (1) |
式中,K值是指对流层天顶湿延迟与PWV之间的水汽转换因子。
有研究表明,K值与高程有一定的相关性[7-8]。因此﹐顾及高程因素影响的Emardson-H模型公式为:
| $ \begin{array}{c} k=a_0+a_1 \varphi+a_2 \sin \left(2 \pi \frac{\text { doy }}{365.25}\right)+ \\ a_3 \cos \left(2 \pi \frac{\text { doy }}{365.25}\right)+a_4 H \end{array} $ | (2) |
式中,φ为大地纬度,doy为年积日,H为海拔(单位m),a0、a1、a2、a3、a4为模型系数。
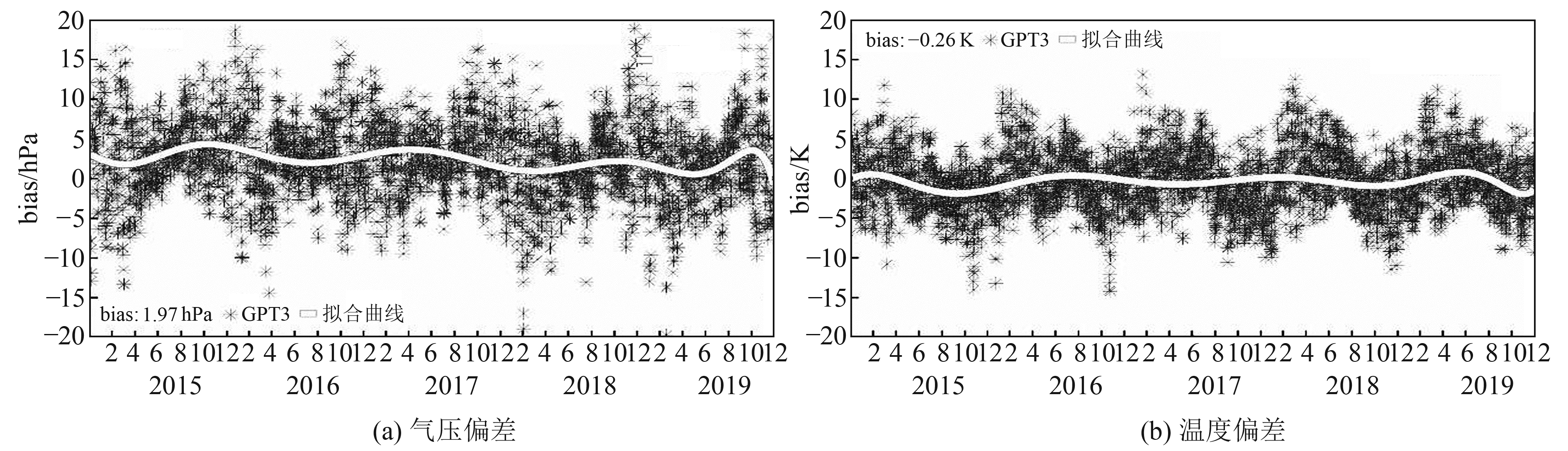
2 GPT3模型的精度分析图 1和2为安庆站与阜阳站2015~2019年使用GPT3模型演算出的气压偏差与温度偏差。由图可知,GPT3模型的气压偏差大多不超过15 hPa,日变化量级处于0~0.1 hPa;气压在不同季节偏差不大,但在相同季节可能出现偏差过大的情况。而温度偏差大部分在±10 K以内,日变化量级处于0~0.1 K,且存在较明显的季节性周期变化,以春夏为起始,温度偏差呈类余弦曲线分布。

|
图 1 2015~2019年安庆站气压偏差和温度偏差 Fig. 1 Air pressure bias and temperature bias of Anqing station from 2015 to 2019 |
|
图 2 2015~2019年阜阳站气压偏差和温度偏差 Fig. 2 Air pressure bias and temperature bias of Fuyang station from 2015 to 2019 |
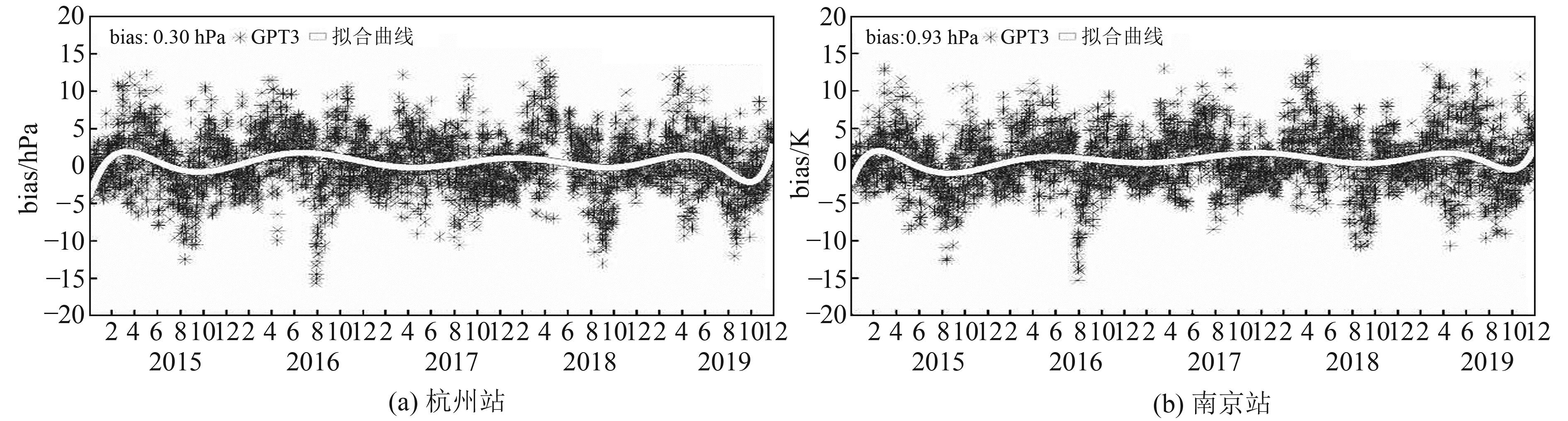
图 3为2015~2019年长三角地区杭州站和南京站的水汽压偏差时序分布。可以看出,各站水汽压偏差大部分在±15 hPa以内,日变化量级处于0~0.15 hPa,也呈现出较明显的季节性周期变化。在夏秋交际与冬春交际时,恶劣天气发生概率较大,导致部分水汽压偏差较大。由曲线图走势可看出:冬春偏正,夏秋偏负。
|
图 3 2015~2019年杭州站和南京站的水汽压偏差 Fig. 3 The bias of vapor pressure at Hangzhouand Nanjing during 2015 to 2019 |
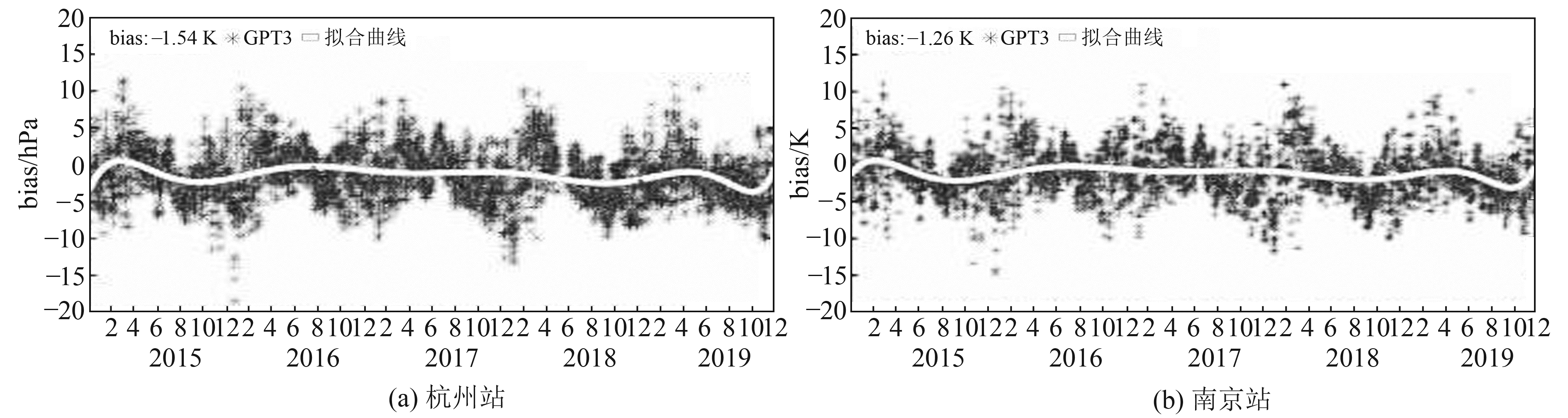
图 4为2015~2019年长三角地区杭州站和南京站Tm偏差时序分布。可以看出,各站Tm偏差大部分也在±15 K以内,日变化量级处于0~0.1 hPa,呈现出的季节性周期变化与温度类似,以春夏为起始,偏差呈类余弦曲线分布。
|
图 4 2015~2019年杭州站和南京站的Tm偏差 Fig. 4 Tm bias of at Hangzhou and Nanjing during 2015 to 2019 |
表 1统计了2017~2019年长三角地区各站点气压、温度、水汽压和Tm的精度。可以看出,其中气压的bias均值为-1.15 hPa,RMS均值为5.09 hPa;温度的bias均值为-0.73 K,RMS均值为3.90 K;水汽压的bias均值为0.76 hPa,RMS均值为4.01 hPa;Tm的bias均值为-1.17 K,RMS均值为4.54 K。由表可知,水汽压的数值大部分为正向偏差,而气压、温度和Tm的数值大部分为负向偏差。
|
|
表 1 2017~2019年GPT3模型气压、温度、水汽压和Tm精度统计 Tab. 1 The precision statistics of air pressure, temperature, vapor pressure and Tm of GPT3 during 2017 to 2019 |
通过对比,本文决定使用收敛结果与最终精度都比较优秀的Emardson-H模型建立GPT3改进模型:
| $ \begin{aligned} f(x)= & a_0+a_1 \varphi+a_2 \sin \left(2 \pi \frac{x}{365.25}\right)+ \\ & a_3 \cos \left(2 \pi \frac{x}{365.25}\right)+a_4 H \end{aligned} $ | (3) |
式中,a0、a1、a2、a3、a4为系数,x为年积日,φ为大地纬度,H为海拔,f(x) 为气象参数偏差。
将2015~2016年长三角地区7个站点GPT3模型的气压、温度、水汽压和Tm等参数偏差分别代入式(3),即可得到关于气压、温度、水汽压和Tm等偏差的Emardson-H模型系数(表 2)。纵向对比拟合系数可知,4个系数差别明显,说明4类气象参数的偏差分布各有特征。
|
|
表 2 2015~2016年气压、温度、水汽压和Tm等参数偏差的Emardson-H模型系数 Tab. 2 Emardson-H model coefficients for bias in air pressure, temperature, water vapor pressure and other parameters during 2015 to 2016 |
利用基于Emardson-H模型建立GPT3改进模型,同时参考探空资料分析改进模型(Improved-GPT3)的精度,并预测2017~2019年各站的气象参数值,评估改进模型季节性周期偏差的改进效果。限于篇幅,图 5和6仅列出安庆站和阜阳站的气压、温度、水汽压和Tm偏差分析结果,由图可知,GPT3改进模型已基本不受季节性周期影响,随季节的波动变化有所减弱,大部分都维持在±10 hPa和±10 K以内。整体来看,GPT3改进模型的精度明显提升。

|
图 5 2017~2019年安庆站的气压、温度、水汽压和Tm偏差时序对比 Fig. 5 Comparison of air pressure, temperature, water vapor pressure and Tm bias time series of Anqing station during 2017 to 2019 |

|
图 6 2017~2019年阜阳站的气压、温度、水汽压和Tm偏差时序对比 Fig. 6 Comparison of air pressure, temperature, water vapor pressure and Tm bias at Fuyang station during 2017 to 2019 |
表 3为2017~2019年长三角地区各模型的参数精度统计。由表可知,GPT3改进模型的气压bias和RMS均值分别为-0.16 hPa和4.64 hPa,比GPT3模型降低了0.99 hPa和0.45 hPa;温度bias和RMS均值分别为0.23 K和3.53 K,比GPT3模型降低了0.50 K和0.37 K;水汽压为0.04 hPa和3.73 hPa,比GPT3模型降低了0.72 hPa和0.28 hPa;Tm为-0.48 K和3.27 K,比GPT3模型降低了0.69 K和1.27 K。改进模型各参数精度均有所提升,且Tm精度的改进稍优于其他3类参数。其中,除上海站气压RMS的改进不明显,其他6个站的参数精度均有所提升,可能是由于2017~2019年上海站的探空资料空缺较多,样本数量较其他站有所减少,导致精度有所欠缺。整体上,基于Emardson-H的GPT3改进模型在平均bias和RMS方面比GPT3模型有更高的精度和可靠性。
|
|
表 3 2017~2019年长三角地区各模型参数精度统计 Tab. 3 Precision statistics of various parameters in the Yangtze river delta during 2017 to 2019 |
表 4为2014年长三角地区各模型精度统计,可以看出,GPT3改进模型的气压bias和RMS均值分别为-0.19 hPa和4.33 hPa,比GPT3模型降低了1.01 hPa和0.45 hPa;温度bias和RMS均值分别为-0.29 K和3.67 K,比GPT3模型降低了0.93 K和0.52 K;水汽压为-0.57 hPa和3.29 hPa,比GPT3模型分别提升0.40 hPa和降低0.16 hPa;Tm为-0.58 K和3.30 K,比GPT3模型降低了0.64 K和0.44 K。改进模型各参数精度均有所提升,且温度的改进稍优于其他3类参数,其中杭州站、上海站和射阳站气压RMS改进不明显,阜阳站水汽压RMS改进不明显。可以看出,基于2015~2016年长三角地区7个探空站数据建立的GPT3改进模型在预测其他年份数据时仍可保持一定的精度。
|
|
表 4 2014年长三角地区各模型精度统计 Tab. 4 Accuracy statistics of various models in the Yangtze river delta in 2014 |
由于长三角地区GPT3模型和探空站资料的气象参数精度存在季节性周期变化,导致气压、温度和水汽压等参数存在偏差,提出一种基于Emardson-H的GPT3改进模型。结果表明:
1) GPT3模型的各参数偏差呈较明显的季节性周期变化,以春夏为起始,气压偏差呈类正弦曲线分布,温度、水汽压和Tm偏差呈类余弦曲线分布,气压、温度、水汽压和Tm的RMS均值分别为5.09 hPa、3.90 K、4.01 hPa和4.54 K。
2) 基于Emardson-H的GPT3改进模型的气压、温度、水汽压和Tm平均偏差较GPT3模型分别提升0.99 hPa、0.50 K、0.72 hPa和0.69 K,RMS均值分别提升0.45 hPa、0.37 K、0.28 hPa和1.27 K,说明GPT3改进模型精度更优。
| [1] |
Boehm J, Heinkelmann R, Schuh H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683 DOI:10.1007/s00190-007-0135-3
(  0) 0) |
| [2] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [3] |
Landskron D, Böhm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
(  0) 0) |
| [4] |
Emardson T R, Derks H J P. On the Relation between the Wet Delay and the Integrated Precipitable Water Vapour in the European Atmosphere[J]. Meteorological Applications, 2000, 7(1): 61-68 DOI:10.1017/S1350482700001377
(  0) 0) |
| [5] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1 069-1 073 DOI:10.1002/grl.50288
(  0) 0) |
| [6] |
Li L, Gao Y, Xu S Y, et al. The New Improved ZHD and Weighted Mean Temperature Models Based on GNSS and Radiosonde Data Using GPT3 and Fourier Function[J]. Atmosphere, 2022, 13(10): 1 648 DOI:10.3390/atmos13101648
(  0) 0) |
| [7] |
高壮, 何秀凤, 常亮. GPT3模型在中国地区的精度分析[J]. 武汉大学学报: 信息科学版, 2021, 46(4): 538-545 (Gao Zhuang, He Xiufeng, Chang Liang. Accuracy Analysis of GPT3 Model in China[J]. Geomatics and Information Science of Wuhan University, 2021, 46(4): 538-545)
(  0) 0) |
| [8] |
李黎, 侯晓玲, 张雯雯, 等. 基于Emardson-H模型的GNSS-PWV转换系数精化[J]. 地球物理学报, 2022, 65(11): 4 225-4 235 (Li Li, Hou Xiaoling, Zhang Wenwen, et al. Refinement of the Conversion Coefficient for GNSS Precipitable Water Vapor Based on the Emardson-H Model[J]. Chinese Journal of Geophysics, 2022, 65(11): 4 225-4 235)
(  0) 0) |
| [9] |
陈香萍, 姚茂华, 杨翼飞. 顾及地形起伏的H模型在中国西部地区的适用性分析[J]. 测绘地理信息, 2020, 45(4): 79-82 (Chen Xiangping, Yao Maohua, Yang Yifei. Applicability Analysis of H Model Considering Topography Fluctuation in Western China[J]. Journal of Geomatics, 2020, 45(4): 79-82)
(  0) 0) |
| [10] |
侯晓玲, 张雯雯, 李黎, 等. 长三角地区GNSS大气水汽转换系数模型精化研究[J]. 大地测量与地球动力学, 2021, 41(1): 17-20 (Hou Xiaoling, Zhang Wenwen, Li Li, et al. Model Refinement of GNSS Atmospheric Water Vapor Conversion Coefficient in Yangtze River Delta[J]. Journal of Geodesy and Geodynamics, 2021, 41(1): 17-20)
(  0) 0) |
| [11] |
郭彬洋, 李黎, 谢威, 等. 长三角地区加权平均温度本地化模型拟合[J]. 导航定位学报, 2019, 7(2): 61-67 (Guo Binyang, Li Li, Xie Wei, et al. Localized Model Fitting of Weighted Mean Temperature in Yangtze River Delta Region[J]. Journal of Navigation and Positioning, 2019, 7(2): 61-67)
(  0) 0) |
| [12] |
刘焱雄, 陈永奇, 刘经南. 利用地面气象观测资料确定对流层加权平均温度[J]. 武汉测绘科技大学学报, 2000, 25(5): 400-404 (Liu Yanxiong, Chen Yongqi, Liu Jingnan. Determination of Weighted Mean Tropospheric Temperature Using Ground Meteorological Measurement[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(5): 400-404)
(  0) 0) |
| [13] |
Duan J P, Bevis M, Fang P, et al. GPS Meteorology: Direct Estimation of the Absolute Value of Precipitable Water[J]. Journal of Applied Meteorology, 1996, 35(6): 830-838 DOI:10.1175/1520-0450(1996)035<0830:GMDEOT>2.0.CO;2
(  0) 0) |
| [14] |
Ingold T, Peter R, Kämpfer N. Weighted Mean Tropospheric Temperature and Transmittance Determination at Millimeter-Wave Frequencies for Ground-Based Applications[J]. Radio Science, 1998, 33(4): 905-918 DOI:10.1029/98RS01000
(  0) 0) |
2. Research Center of Beidou Navigation and Environmental Remote Sensing, Suzhou University of Science and Technology, 99 Xuefu Road, Suzhou 215009, China
 2023, Vol. 43
2023, Vol. 43


