2. 成都信息工程大学资源环境学院,成都市学府路24号,610225
研究表明,GNSS对流层延迟(zenith total delay, ZTD)随海拔的增加而减小。杨晶等[1]通过选取不同海拔的测站进行分析发现,在海拔大于1 000 m的地区,对流层延迟量随海拔增加而减小的特征更为明显;陈钦明等[2]沿经度和纬度对中国区域的对流层延迟变化进行定量分析和研究发现,对流层延迟的变化特征主要取决于测站位置处的纬度和高程,与经度无关。此外,GNSS对流层延迟具有显著的年周期变化、季节性变化及日变化特征[3]。Jin等[4]分析了全球150个IGS站8 a的对流层延迟时间序列发现,不同海拔地区的对流层延迟活动特性存在显著差异。曲伟菁[5]通过比较现有对流层延迟模型精度随高程的变化,得出现有模型在高海拔地区的适用性降低的结论。闫小霞等[6]利用陆态网对流层产品评定对流层延迟格网产品精度发现,在地形起伏较大的中国西部地区,格网产品精度存在较大的正偏差。谭勇等[7]发现常用的对流层延迟模型在高海拔地区精度降低,各模型的精度具有季节性特征。高玉东等[8]利用实测气象参数进行对流层延迟改正后发现,该方法可有效提高高原地区的卫星导航定位精度。
近年来,我国在高原地区的重大工程建设项目日益增多,对GNSS高精度位置服务的需求随之增加,高原地区特有的气象条件和对流层延迟特性对GNSS定位的影响急需得到重视。因此,本文利用高海拔地区地基GNSS观测资料,探讨对流层延迟的变化特征及其与气象要素的关系,并分析对流层延迟模型对GNSS定位的影响水平,为构建适用于高海拔地区的精细化对流层延迟校正模型提供参考。
1 实验数据与方法 1.1 实验数据为研究高海拔地区GNSS对流层延迟的时空特性,本文选择2020年高海拔地区24个测站为期1 a的地基GNSS观测数据,测站平均海拔为3 995 m。同时,在同等纬度条件下选择成都周边6个测站的同期观测数据,以对比高、低海拔地区对流层延迟模型的差异,低海拔地区测站平均海拔为656 m,最高897 m,最低409 m。各测站数据完整率都在95%以上,均能准确反映对流层延迟随时间的变化情况。
1.2 对流层延迟反演方法当GNSS信号穿过大气层时,受到对流层折射的影响,在天顶方向产生的路径延迟等效距离约为2.3 m[9]。Hopfield[10]提出对流层延迟包含对流层干延迟(zenith hydrostatic delay, ZHD)和对流层湿延迟(zenith wet delay, ZWD)两个部分。对不同高度的卫星,需要引入映射函数来确定信号路径上的对流层延迟量:
| $ \mathrm{ZTD}=10^{-6} \int_0^{\infty} N(s) \mathrm{d} s $ | (1) |
| $ \begin{array}{c} \mathrm{ZTD}(\mathrm{EL})=\mathrm{ZHD} \times \mathrm{DMAP}(\mathrm{EL})+ \\ \mathrm{ZWD} \times \mathrm{WMAP}(\mathrm{EL}) \end{array} $ | (2) |
式中,N为对流层的大气折射率,s为信号传播的路径,EL为卫星高度角,DMAP为干延迟映射函数,WMAP为湿延迟映射函数。
为准确获取测站位置处的对流层延迟量,本文基于高精度数据处理软件GAMIT对实验区域的对流层延迟进行反演。GAMIT软件反演ZTD使用分段线性法(piece-wise linear, PWL)求解,用离散随机过程来表示对流层延迟随时间的变化特征,最后由估算出的ZTD减去由经验模型计算出的ZHD,得到对流层湿延迟。Saastamoinen模型与Hopfield模型利用地面的气象资料、测站高程与纬度等数据计算对流层延迟[11]:
| $ \left\{\begin{array}{l} \mathrm{ZTD}_s=\frac{0.002\;277}{\text{sin} \varepsilon}\left[P_s+\left(\frac{1\;255}{T_s}+0.05\right) \times\right. \\ \left.\quad e_s-\frac{B}{\tan ^2 \varepsilon}\right] W\left(\varphi, h_s\right)+\delta R \\ W\left(\varphi, h_s\right)=1+0.002\;6 \cos 2 \varphi+0.000\;28 h_s \end{array}\right. $ | (3) |
| $ \begin{aligned} \mathrm{ZTD}_H= & 1.552 \times 10^{-5} \times \frac{P_s}{T_s} \times\left(H_d-h_s\right)+ \\ & 0.074\;65 \times \frac{e_s}{T_{s}^{2}} \times\left(H_w-h_s\right) \end{aligned} $ | (4) |
式中,Ps为地面大气压,Ts为地面温度,hs为测站处海拔,es为地面水汽压,B为与hs有关的参数,δR为与ε、hs有关的参数,φ为测站处纬度,Hd与Hw分别为对流层干、湿顶层的高度。
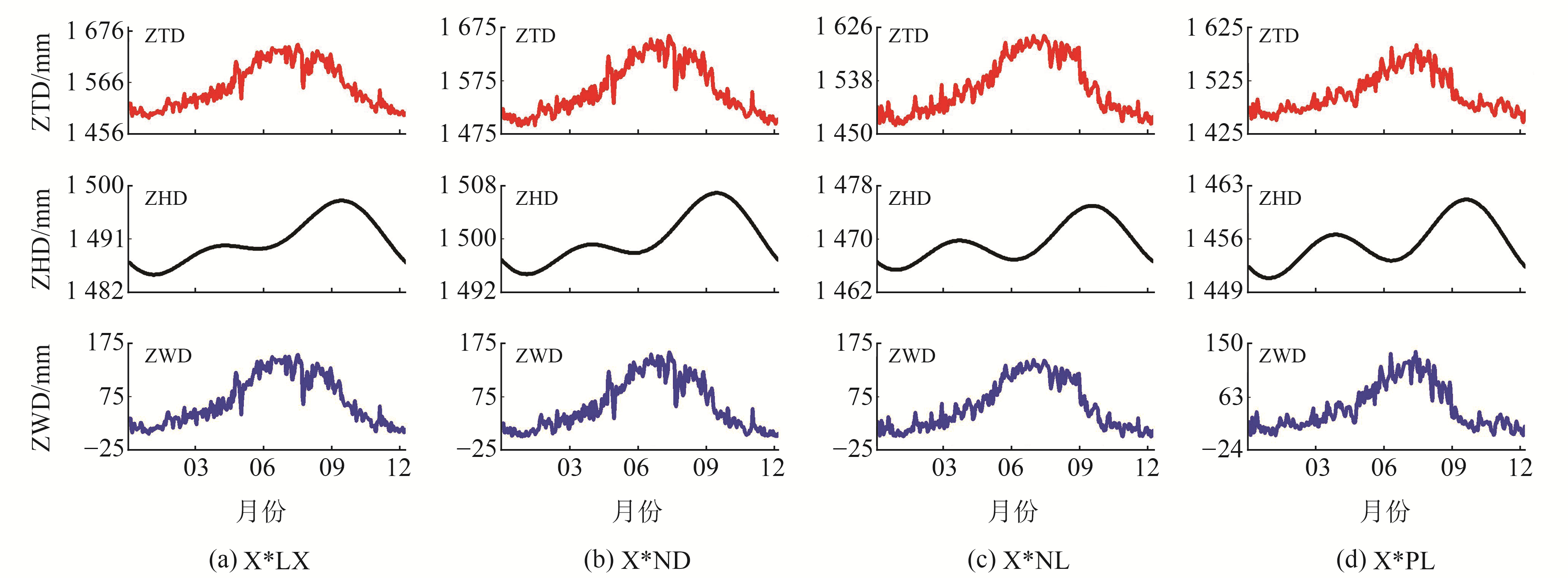
2 高海拔地区对流层延迟的时空特性 2.1 时序变化特性通过软件解算得到高海拔地区X*ND、X*LX、X*NL与X*PL四个测站2020年对流层延迟时序数据,以此分析ZTD、ZHD与ZWD的变化特征。图 1为2020年高海拔地区GNSS测站对流层延迟日变化,可以看出,各GNSS测站之间的对流层延迟变化总体趋势基本一致。高海拔地区ZTD与ZWD的变化趋势极为相似,全年时间序列变化特征总体呈单峰趋势:延迟量由低到高先增加,到达峰值后再逐渐降低,总体呈抛物线式的变化特征,但在局部出现显著波动,表明ZTD和ZWD在较短时间尺度上的变化十分显著。而高海拔地区ZHD的变化呈双峰趋势:延迟量先逐渐增加到一个较低的峰值后降低,再增大并达到一个较高的峰值,最后逐渐降低,其时序曲线较为光滑,无局部波动特征,表明高海拔地区ZHD在短时间内较为稳定。
|
图 1 高海拔地区对流层延迟的日变化特征 Fig. 1 Diurnal variation of tropospheric delayin high altitude areas |
ZTD与ZWD值在2~7月迅速增加,8月达到全年峰值,分别为1 625 mm、146 mm;9月开始,ZTD、ZWD值逐渐减小,至11月下降幅度分别为113 mm、112 mm;12月开始ZTD、ZWD值继续缓慢下降,到1月维持在一年中的最低位置。ZHD的变化幅度很小(全年变幅仅为11 mm),在2~9月都保持缓慢上升趋势,最大值出现在10月,11~12月为下降阶段,1月为全年最低阶段。
为进一步分析对流层干、湿延迟的变化特征,计算2020年4个高海拔测站的对流层延迟均值,并分别统计干湿延迟占总延迟比(ZHD/ZTD、ZWD/ZTD)、干湿延迟的变化幅度及干湿延迟与总延迟的相关系数,如表 1所示。可以看出,对流层干延迟ZHD占总延迟比很大,为96.3%,但波动很小,4个测站的ZHD在1 a内的变化幅度分别为12.6 mm、12.3 mm、9.6 mm、11 mm;与之相反,对流层湿延迟ZWD占总延迟比很小(3.7%),但波动却很剧烈,平均变化幅度为147.3 mm,是ZHD变化幅度的13倍。另外,由表 1中干湿延迟与总延迟的相关系数可知,ZHD与ZTD的相关性小于0.1,而ZWD与总延迟的相关系数达到0.99以上。综上表明,高海拔地区对流层干延迟为主要成分,对流层延迟时序变化特征与湿延迟的波动密切相关。
|
|
表 1 高海拔地区对流层延迟干湿分量特征 Tab. 1 Characteristics between dry and wet components of tropospheric delayin high altitude areas |
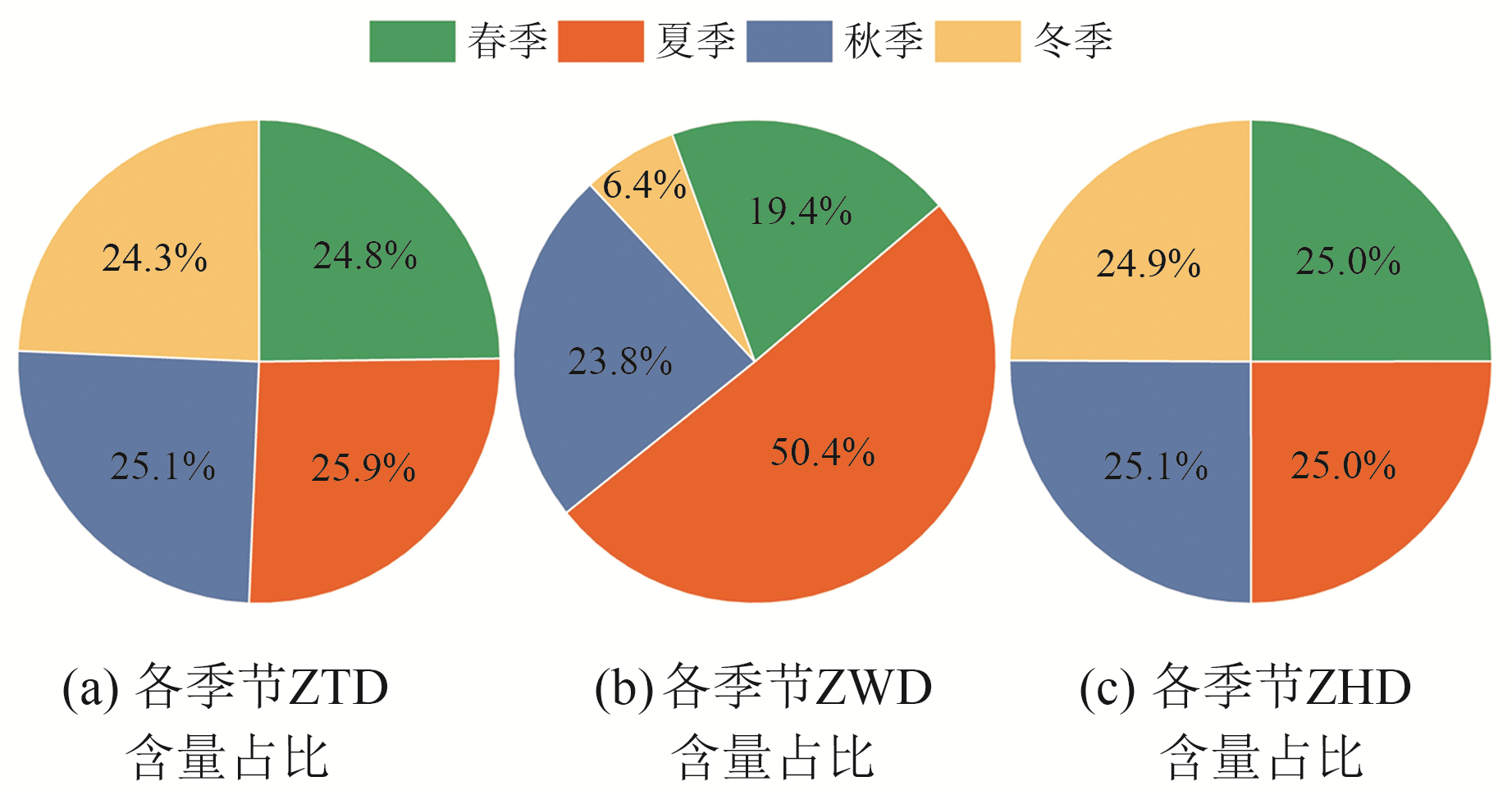
为分析不同季节高海拔地区对流层延迟的活动特征,分别对24个测站2020年不同季节的ZTD、ZWD、ZHD均值进行统计,结果如图 2所示。整体上看,ZTD与ZHD并无明显的季节性差异,二者的含量在4个季节中分布均匀,均占25%左右。而ZWD在4个季节中的占比呈现出夏季大、冬季小的季节性特征:夏季的ZWD值占全年总量的50.4%;春、秋季次之,各占全年总量的19%与24%;冬季最小,仅占全年总量的6%。综上,在高海拔地区仅ZWD呈现出显著的季节性特征,即夏季最大(101.7 mm),其次是秋季(47.9 mm)与春季(39.1 mm),冬季最小(12.9 mm),而ZTD和ZHD的季节性差异并不明显。
|
图 2 对流层延迟季节分布特征饼状图 Fig. 2 Pie chart of seasonal distribution characteristics of tropospheric delay |
研究表明,高海拔地区对流层延迟的短期变化主要由ZWD的波动决定,因此本文选取2020年24个高海拔GNSS测站资料来研究ZWD的季节性空间分布特征。将各测站的ZWD分别按季节求均值,再通过可调节张量连续曲率样条插值法对所有站点的ZWD值作插值处理,得到研究区域不同季节的ZWD分布情况,如图 3所示。

|
图 3 研究区域2020年各季节的ZWD空间分布 Fig. 3 The spatial distribution of ZWD in each seasonof 2020 in the studied area |
由图 3可知,研究区内不同季节的ZWD均存在空间分布差异:总体上看,ZWD具有夏季高、冬季低的季节性特征,这与§2.2.1的结论相符;且ZWD在空间分布上呈明显的东南高、西北低的态势,而研究区东南方向在不同季节均存在一个ZWD高值区。分析发现,该高值区域位于喜马拉雅南麓,平均海拔仅1 200 m,是整个青藏高原海拔最低的地方,属于亚热带湿润气候区,年平均降水量可达2 071 mm,是全国年平均降水量的3.2倍[12],而研究区的其他区域海拔普遍在4 500 m以上,年降水量仅有100~150 mm。综上表明,海拔及气象条件是导致ZWD空间分布出现差异的关键因素,且研究区内存在显著的对流层延迟局部空间分布差异,为提高GNSS在高海拔地区的定位精度,有必要建立精细化的对流层延迟模型。
2.3 高低海拔地区对流层延迟差异在高海拔地区(平均海拔3 724 m)与成都市周边区域(平均海拔464 m)分别选择4个GNSS测站,以探究同纬度条件下高、低海拔地区之间的对流层延迟差异。对2020年高、低海拔地区各站点ZTD与ZWD日变化的中位数、四分位数、均值和极值等数据进行统计,绘制高、低海拔地区各测站的ZTD与ZWD箱形图(图 4)。可以看出,高、低海拔地区对流层延迟差异十分明显,其中ZWD均值相差122 mm,ZTD均值相差786 mm,高海拔地区ZTD平均含量是低海拔地区的67%、ZWD平均含量只有低海拔地区的30%。此外,高、低海拔地区对流层延迟的年变化幅度也有明显差异,高、低海拔地区ZTD年平均变化幅度分别为146 mm与307 mm,二者的ZWD年平均变化幅度相差110 mm。

|
图 4 2020年高、低海拔地区各测站ZTD与ZWD箱形图 Fig. 4 Box chart of ZTD and ZWD of stations at high and low altitudes in 2020 |
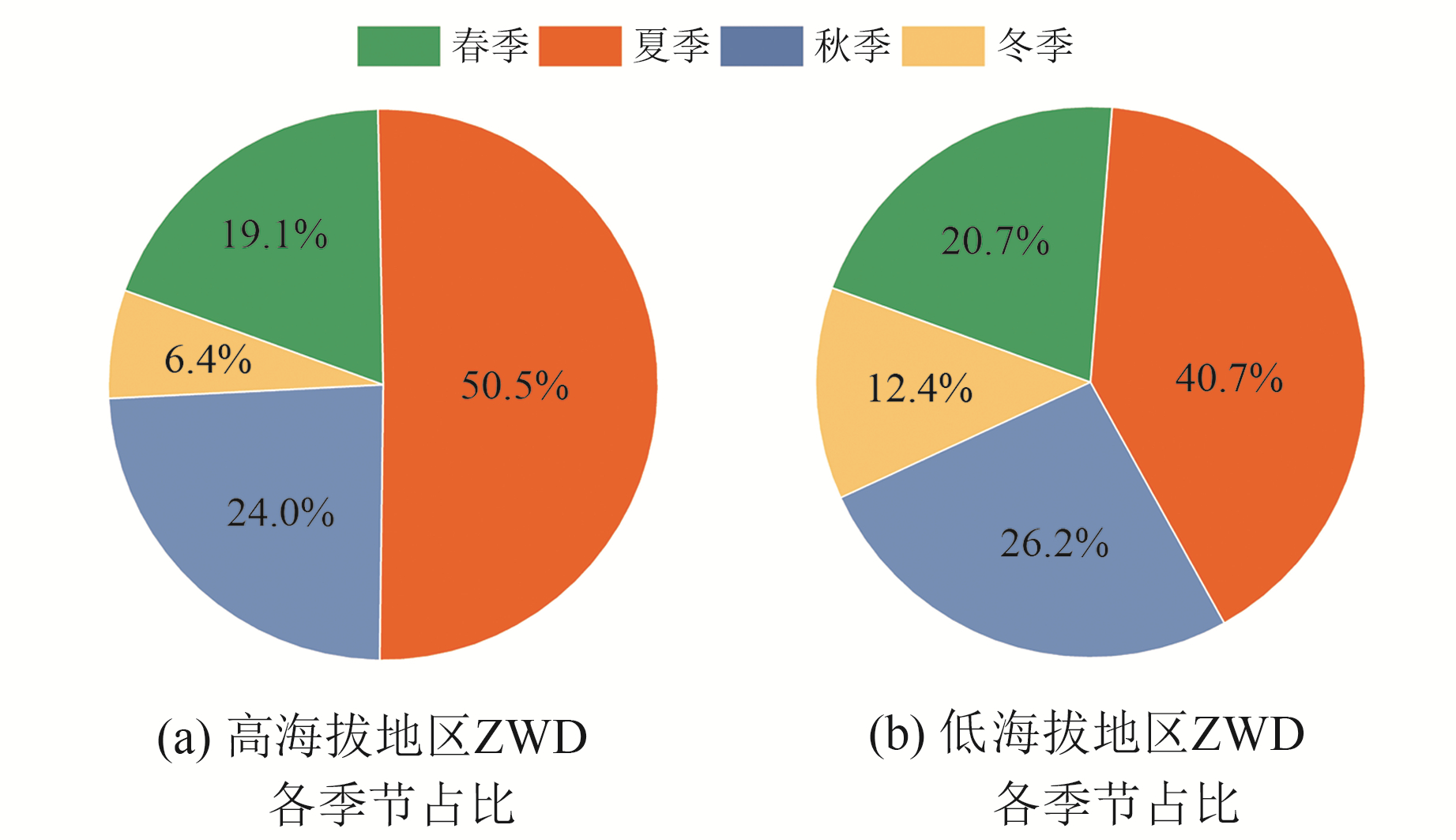
此外,对高、低海拔地区ZWD在1 a中各个季节的平均占比进行了分析,如图 5所示。ZWD在夏、冬两季的占比差异明显,春、秋两季相差不大:在高海拔地区,夏季ZWD占全年的50.4%,而低海拔地区为40.7%;冬季的ZWD全年最低,在高、低海拔地区分别占6.4%、12.4%,低海拔地区比高海拔地区高出1倍左右;高、低海拔地区ZWD在春、秋两季的占比差异很小,分别是19.1%、24% 与20.7%、26.2%。此外,高、低海拔地区之间ZWD的季节性差异在夏季最大(185 mm)、冬季最小(77mm),春、秋季差异都在100 mm以上。综上,高、低海拔地区的对流层延迟量存在显著差异,且ZWD在高、低海拔地区显示出不同的季节性特征。
|
图 5 高、低海拔地区ZWD季节分布特征 Fig. 5 Seasonal distribution of ZWD in high and low altitudes areas |
为探究高海拔地区对流层延迟模型的性能,选取LHAZ站(海拔3 625 m)2020-01的观测数据与测站配套气象数据(包含气压、气温、相对湿度等参数),数据时间分辨率为2 h。将测站处的气象数据代入Saastamoinen与Hopfield两种对流层延迟模型中计算ZTD值,并将GAMIT软件反演出的对流层延迟作为参考值,使用均方根(RMS)与平均偏差(bias)来评价模型解算的ZTD精度,同时对比低海拔地区HKWS测站(海拔63.7 m)的情况。
图 6为两种对流层延迟模型的计算值与GNSS反演的ZTD参考值之间的时间序列对比,表 2为模型值与参考值的平均bias与RMS。结果表明,利用实测气象参数计算Saastamoinen模型与Hopfield模型的ZTD值与GNSS反演的结果基本相符,整体变化趋势也保持一致。由表 2可见,Saastamoinen模型的平均bias与RMS在高、低海拔地区均小于Hopfield模型,且高海拔地区Hopfield模型的精度较差,bias与RMS均大于12 cm,说明Saastamoinen模型的性能优于Hopfield模型。

|
图 6 高、低海拔地区ZTD模型值的时间序列与偏差 Fig. 6 Time series and deviations of ZTD model values in high and low altitudes areas |
|
|
表 2 高、低海拔地区ZTD模型值的平均bias与RMS统计 Tab. 2 Average bias and RMS statistics for ZTD model values in high and low altitudes areas |
对比高、低海拔地区的结果发现,在低海拔地区两种模型的计算结果较为接近,二者的bias与RMS均不超过4 cm,有较好的精度。但相较于低海拔地区,Hopfield模型在高海拔地区的bias与RMS分别增大10.8 cm与9.5 cm,Saastamoinen模型分别增大2.7 cm与1.0 cm,可见这两种模型在高海拔地区的适应性都有所降低,且Hopfield模型更为明显。综上表明,常规对流层延迟模型在低海拔地区的性能总体优于高海拔地区,有必要建立适用于高海拔地区的精细化对流层延迟模型。
4 结语高海拔地区的对流层延迟时空特性是建立高原区域性对流层延迟精细化模型的基础。因此,本文利用高海拔地区地基GNSS观测资料反演研究区对流层总延迟、干延迟、湿延迟,研究高海拔地区GNSS对流层延迟时空特征,并分析常规对流层模型在高海拔地区的性能。相关研究结论如下:
1) 高海拔地区ZTD的短期变化与ZWD的波动密切相关,两者的相关系数达到0.99以上。ZTD与ZWD呈现出夏季高、冬季低的季节性变化特征,且高、低海拔地区的对流层延迟存在显著差异,高海拔地区ZTD、ZWD平均含量是低海拔地区的67%与30%。
2) Saastamoinen模型的计算精度在高、低海拔地区均优于Hopfield模型,且两种模型在高海拔地区的适应性都有所降低,Hopfield模型表现更为明显,表明常规对流层延迟模型在低海拔地区的性能要优于高海拔地区。
| [1] |
杨晶, 顾慧, 刘严萍, 等. 基于小波分析的GPS对流层延迟变化研究[J]. 测绘通报, 2015(5): 60-62 (Yang Jing, Gu Hui, Liu Yanping, et al. Study on GPS Tropospheric Delay Variation Based on Wavelet Analysis[J]. Bulletin of Surveying and Mapping, 2015(5): 60-62)
(  0) 0) |
| [2] |
陈钦明, 宋淑丽, 朱文耀. 亚洲地区ECMWF/NCEP资料计算ZTD的精度分析[J]. 地球物理学报, 2012, 55(5): 1 541-1 548 (Chen Qinming, Song Shuli, Zhu Wenyao. An Analysis of the Accuracy of Zenith Tropospheric Delay Calculated from ECMWF/NCEP Data over Asian Area[J]. Chinese Journal of Geophysics, 2012, 55(5): 1 541-1 548)
(  0) 0) |
| [3] |
唐超华, 李陶, 施闯, 等. 天津地区CORS站天顶对流层延迟年周期变化研究[J]. 大地测量与地球动力学, 2009, 29(2): 106-110 (Tang Chaohua, Li Tao, Shi Chuang, et al. Annual Period Changes of Zenith Tropospheric Delay of CORS Stations in Tianjin District[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 106-110)
(  0) 0) |
| [4] |
Jin S G, Park J U, Cho J H, et al. Seasonal Variability of GPS-Derived Zenith Tropospheric Delay(1994-2006) and Climate Implications[J]. Journal of Geophysical Research, 2007, 112(D9)
(  0) 0) |
| [5] |
曲伟菁. 中国地区GPS中性大气天顶延迟研究及应用[D]. 上海: 中国科学院上海天文台, 2007 (Qu Weijing. Research and Application of GPS Neutral Zenith Delay in China Area[D]. Shanghai: Shanghai Astronomical Observatory, CAS, 2007)
(  0) 0) |
| [6] |
闫小霞, 李薇, 张宝成, 等. 基于ECMWF再分析地表资料计算中国区域ZTD的精度分析[J]. 大地测量与地球动力学, 2019, 39(11): 1 142-1 147 (Yan Xiaoxia, Li Wei, Zhang Baocheng, et al. Analysis of the Accuracy of Zenith Tropospheric Delay Calculated by ECMWF Surface Data over China Area[J]. Journal of Geodesy and Geodynamics, 2019, 39(11): 1 142-1 147)
(  0) 0) |
| [7] |
谭勇, 姚宜斌. 常用对流层延迟修正模型的适用性分析及精化[J]. 测绘科学, 2022, 47(6): 15-20 (Tan Yong, Yao Yibin. Applicability Analysis and Refinement of Tropospheric Delay Correction Models[J]. Science of Surveying and Mapping, 2022, 47(6): 15-20)
(  0) 0) |
| [8] |
高玉东, 谢霆锋. 中国气象参数建模与仿真在卫星导航中的应用[J]. 测绘科学技术学报, 2011, 28(1): 10-13 (Gao Yudong, Xie Tingfeng. Meteorological Data of China Modeling and Simulation Analysis in Satellite Positioning Application[J]. Journal of Geomatics Science and Technology, 2011, 28(1): 10-13)
(  0) 0) |
| [9] |
黄丁发, 张勤, 张小红. 卫星导航定位原理[M]. 武汉: 武汉大学出版社, 2015 (Huang Dingfa, Zhang Qin, Zhang Xiaohong. Principle of Satellite Navigation and Positioning[M]. Wuhan: Wuhan University Press, 2015)
(  0) 0) |
| [10] |
Hopfield H S. Tropospheric Effect on Electromagnetically Measured Range: Prediction from Surface Weather Data[J]. Radio Science, 1971, 6(3): 357-367
(  0) 0) |
| [11] |
李国平, 黄丁发, 郭洁, 等. 地基GPS气象学[M]. 北京: 科学出版社, 2010 (Li Guoping, Huang Dingfa, Guo Jie, et al. Ground-Based GPS Meteorology[M]. Beijing: Science Press, 2010)
(  0) 0) |
| [12] |
旺杰, 德庆央宗, 旦增, 等. 2012-2018西藏"雨窝"降水特征及其成因分析[J]. 气象科技, 2021, 49(2): 211-217 (Wang Jie, De Qingyangzong, Dan Zeng, et al. Analysis on Precipitation Characteristics and Causes of Rain Nest in Tibet from 2012 to 2018[J]. Meteorological Science and Technology, 2021, 49(2): 211-217)
(  0) 0) |
2. Faculty of Resources and Environment, Chengdu University of Information Technology, 24 Xuefu Road, Chengdu 610225, China
 2023, Vol. 43
2023, Vol. 43


